Похожие презентации:
Алгебраические поверхности второго порядка. Уравнения и геометрическое изображение
1.
Алгебраические поверхности второгопорядка. Уравнения и геометрическое
изображение
2.
x2 y 22 1
2
a
b
2
x
y2
2 1
2
a
b
1
2
3
эллиптический цилиндр
гиперболический цилиндр
параболический цилиндр
4
x2 y 2
z 2 2,
a
b
эллиптический параболоид
5
x2
y2
z 2 2,
a
b
гиперболический параболоид
6
x2 y 2 z 2
2 2 1,
2
a
b
c
x2 y 2 z 2
2 2 0,
2
a
b
c
7
8
9
x2 y 2 z 2
2 2 1,
2
a
b
c
x2
2
y2
2
z2
2
1
эллипсоид
конус второго порядка
однополостный гиперболоид
двуполостный гиперболоид
3.
x2 y 22 1
2
a
b
x2 y 2
2 1
2
a
b
1
2
эллиптический цилиндр
гиперболический цилиндр
параболический цилиндр
3
4
5
6
7
2
2
x
y
z 2 2,
a
b
x2
y2
z 2 2,
a2 b2
2
x
y
z
2 2 1,
2
a
b
c
2
2
x
y
z2
2 2 0,
2
a
b
c
8
x2
y2 z2
2 2 1,
2
a
b
c
9
x2
2
y2
2
z2
2
1
эллиптический параболоид
гиперболический параболоид
эллипсоид
конус второго порядка
однополостный гиперболоид
двуполостный гиперболоид
4.
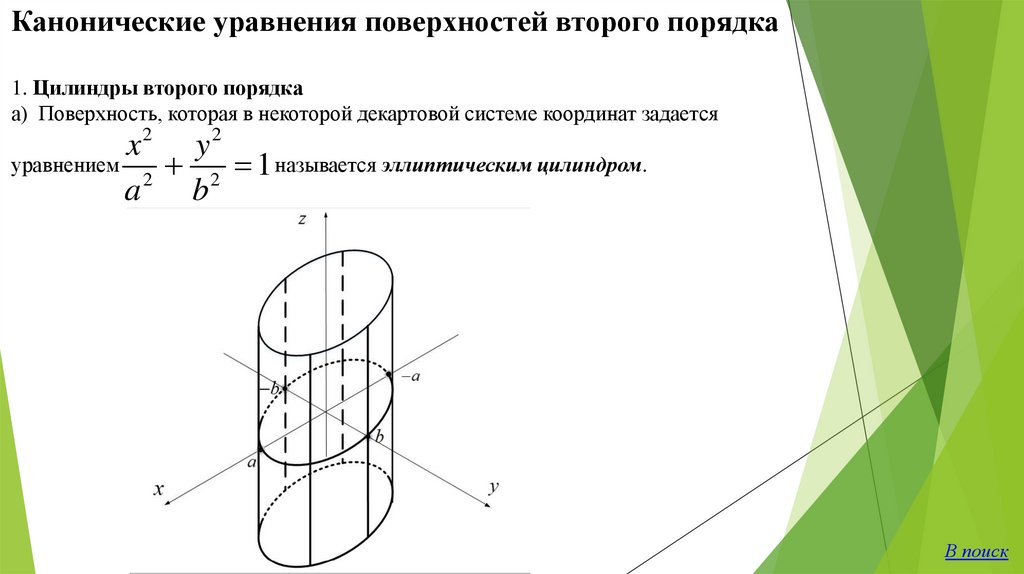
Канонические уравнения поверхностей второго порядка1. Цилиндры второго порядка
а) Поверхность, которая в некоторой декартовой системе координат задается
x2 y 2
уравнением
2 1 называется эллиптическим цилиндром.
2
a
b
В поиск
5.
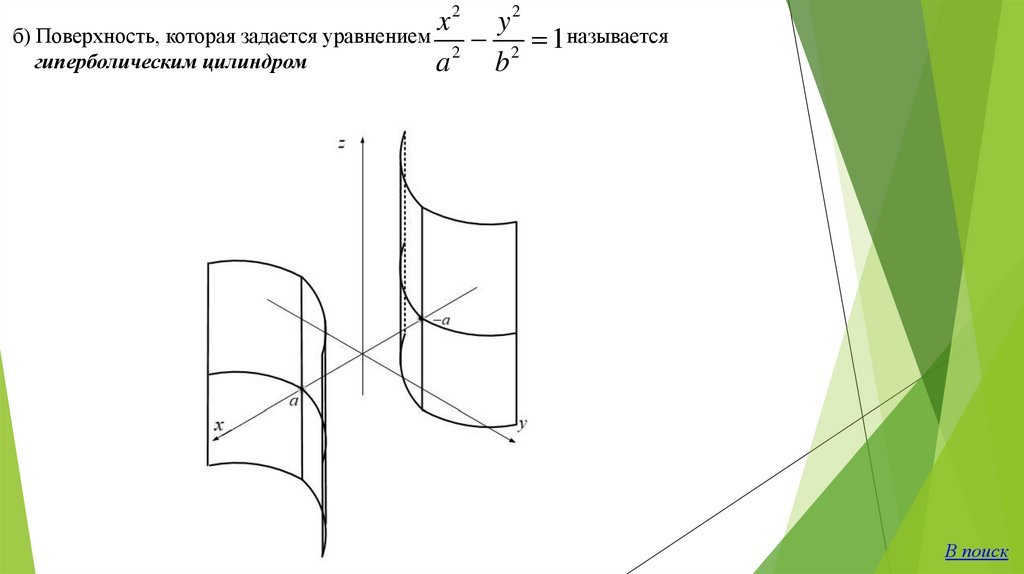
22
x
y
б) Поверхность, которая задается уравнением
2 1 называется
2
гиперболическим цилиндром
a
b
В поиск
6.
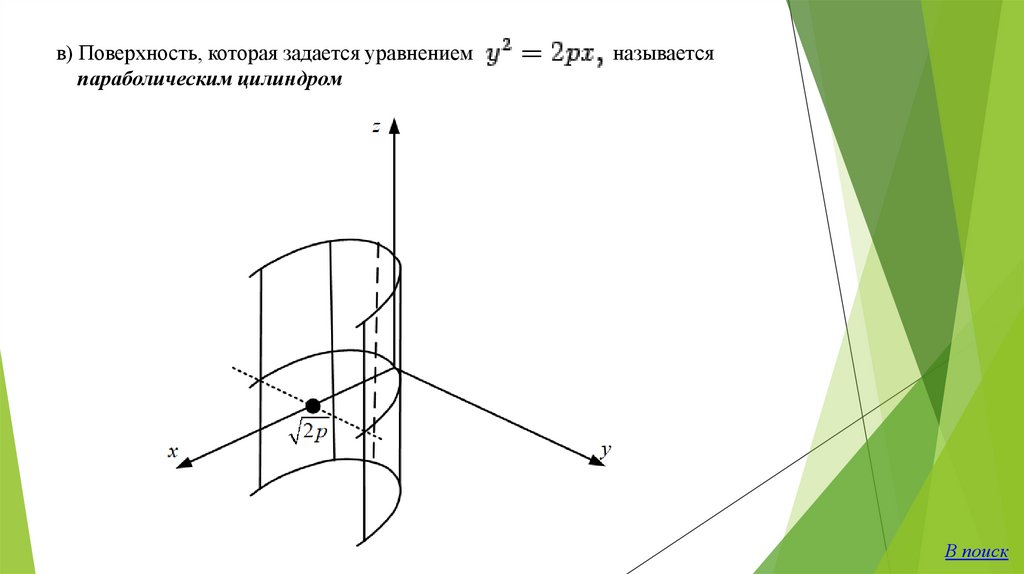
в) Поверхность, которая задается уравнениемпараболическим цилиндром
называется
В поиск
7.
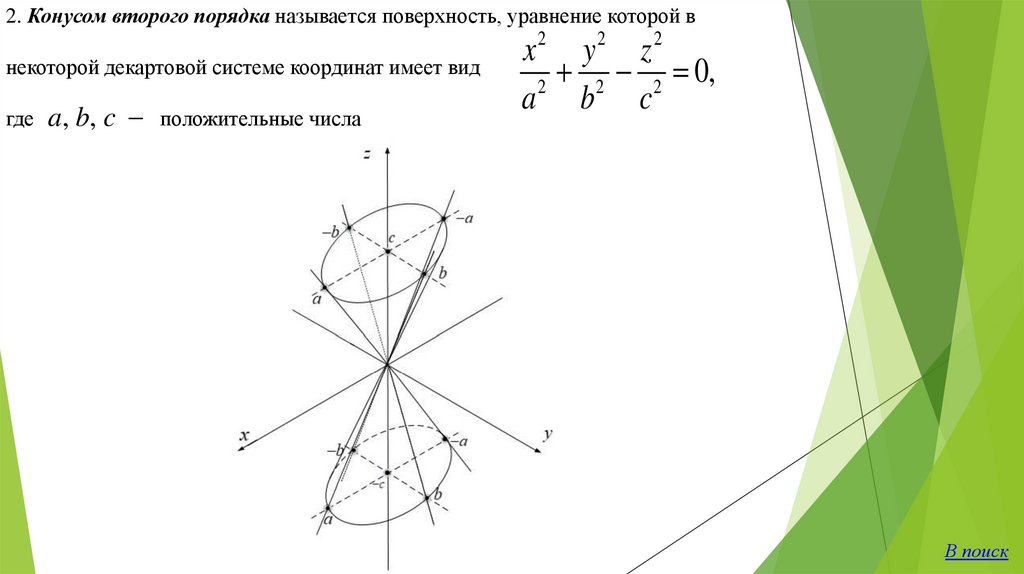
2. Конусом второго порядка называется поверхность, уравнение которой в2
2
2
с
некоторой декартовой системе координат имеет вид
где a, b, c положительные числа
x y z
2 2 0,
2
a b c
В поиск
8.
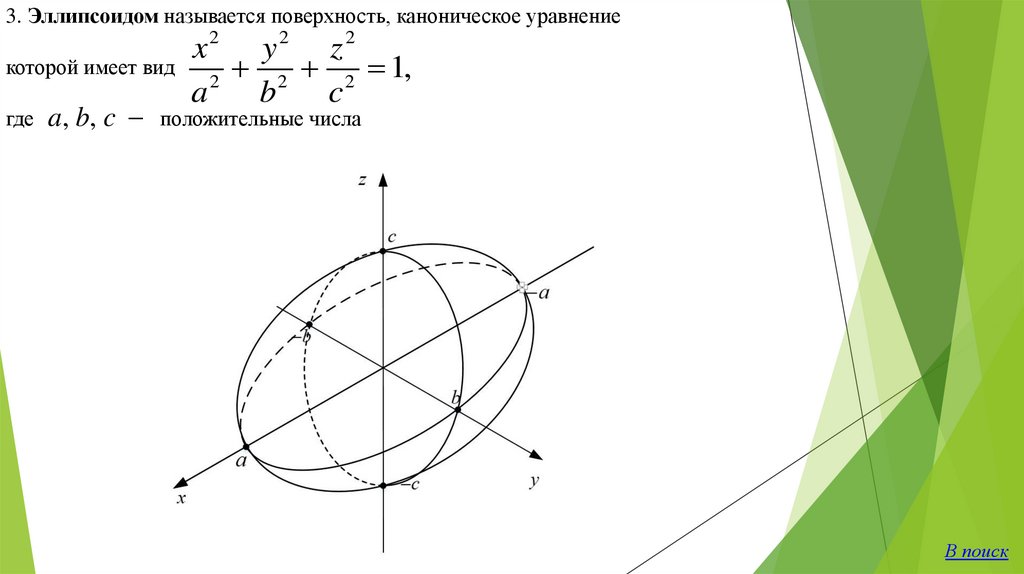
3. Эллипсоидом называется поверхность, каноническое уравнениеx2 y 2 z 2
которой имеет вид
2 2 1,
2
a
b
c
где a, b, c положительные числа
В поиск
9.
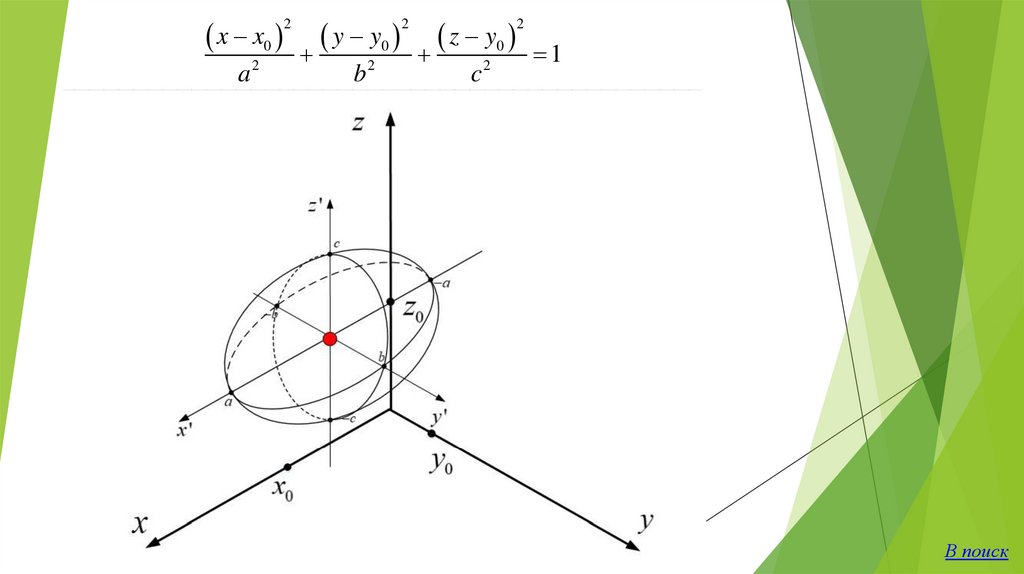
x x0 y y0 z y0 1a2
b2
c2
2
2
2
В поиск
10.
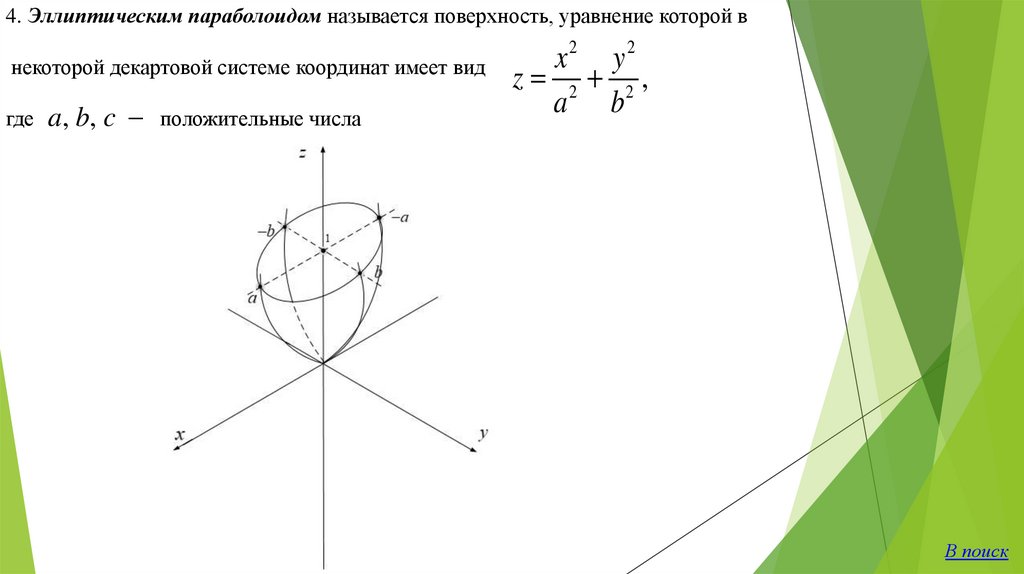
4. Эллиптическим параболоидом называется поверхность, уравнение которой внекоторой декартовой системе координат имеет вид
где a, b, c положительные числа
2
2
x y
z 2 2,
a b
В поиск
11.
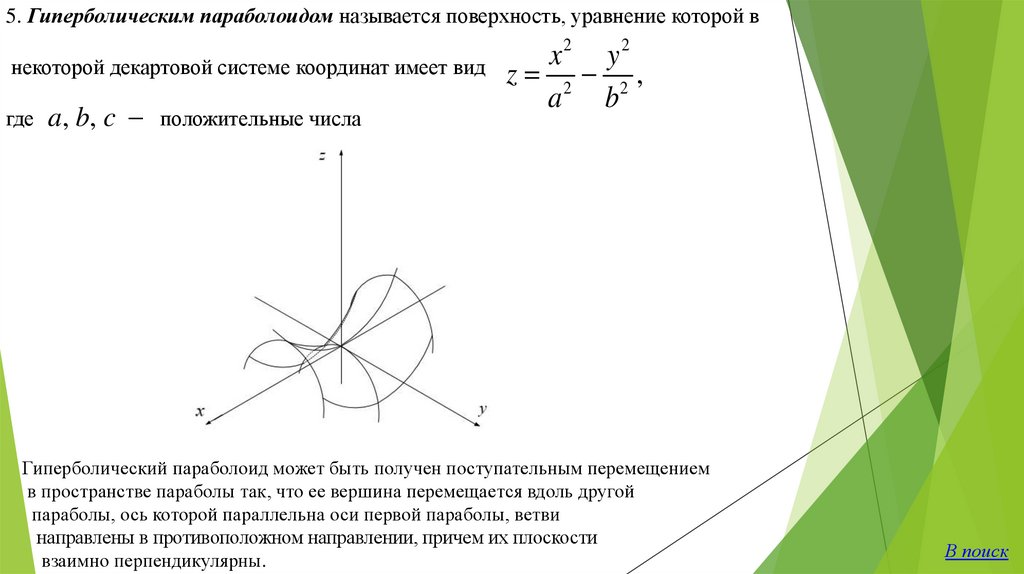
5. Гиперболическим параболоидом называется поверхность, уравнение которой в2
2
x
y
некоторой декартовой системе координат имеет вид z
2,
2
a b
где a, b, c положительные числа
Гиперболический параболоид может быть получен поступательным перемещением
в пространстве параболы так, что ее вершина перемещается вдоль другой
параболы, ось которой параллельна оси первой параболы, ветви
направлены в противоположном направлении, причем их плоскости
взаимно перпендикулярны.
В поиск
12.
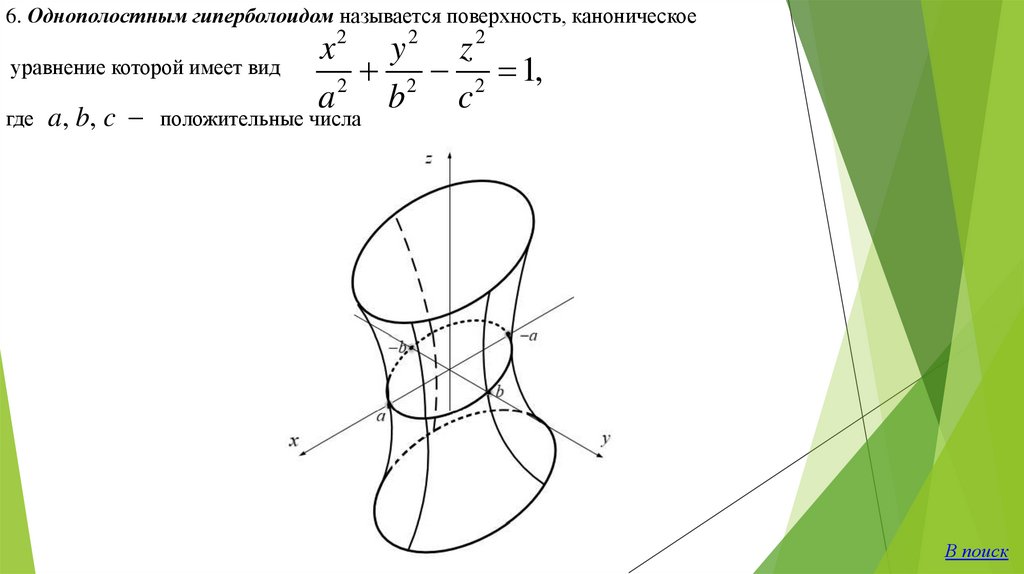
6. Однополостным гиперболоидом называется поверхность, каноническое2
уравнение которой имеет вид
2
2
x
y
z
2 2 1,
2
a
b
c
где a, b, c положительные числа
В поиск
13.
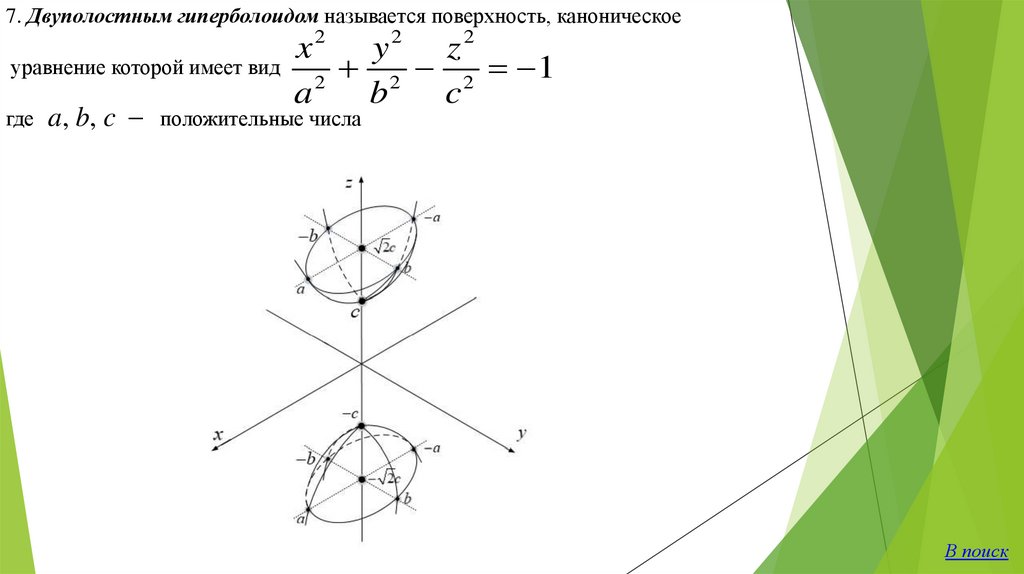
7. Двуполостным гиперболоидом называется поверхность, каноническоеx2 y 2 z 2
уравнение которой имеет вид
2 2 1
2
a
b
c
где a, b, c положительные числа
В поиск



 Математика
Математика








