Похожие презентации:
Вычисление определенных интегралов с помощью теории вычетов
1.
§19. Вычисление определенныхинтегралов с помощью
теории вычетов
п.1. Вычисление интегралов от
тригонометрических рациональных
функций.
Рассмотрим интеграл вида 2
0
R(cos , sin )d ,
где R(u, v) — действительная рациональная
функция двух действительных переменных u и
v, причем R(u, v) непрерывна при [0,2 ].
2.
Замена:Тогда
i
z e .
i
i
1
e e
z z
cos
,
2
2
i
i
1
e e
z z
sin
,
2i
2i
i
dz ie d ,
dz izd ,
dz
d .
iz
3.
Кроме того, при изменении от 0 до 2i
точка z e опишет один раз единичную
окружность | z | 1 в положительном
направлении.
Поэтому
2
z z 1 z z 1 dz
.
R(cos , sin )d
R
,
2
iz
2
i
0
| z| 1
4.
Заметим, что функция1
1
1 z z
z z
f ( z) R
,
iz 2
2i
является рациональной, аналитической на
контуре | z | 1 и внутри его может иметь лишь
конечное число особых точек.
Значит, интеграл
z z 1 z z 1 dz
R
,
2
iz
2
i
| z| 1
Значит, интеграл можно найти с помощью
вычетов.
5.
Пример 1. Вычислить интеграл2
I
0
Решение. Положим
i
z e ,
Тогда
d
.
2 cos
z z
cos
2
dz
d .
iz
,
2
dz
I
.
2
1
i
z
4
z
1
z
z
| z| 1 2
| z| 1
iz
2
dz
1
6.
Найдем особые точкиz 4 z 1 0,
2
z1 2 3, z2 2 3 — простые
Так как
полюсы.
| z1 | 1, | z2 | 1,
то по теореме 1 § 18
2
dz
2
I 2
2 i res f ( z ),
z=z1
i |z| 1 z 4 z 1 i
где
f ( z)
1
z 4z 1
2
.
7.
Найдем вычетz z1
1
1
res f ( z ) lim 2
lim
.
z z1 z 4 z 1
z z1 2 z 4
z z1
2 3
Окончательно заключаем, что
2
1
2
I 2 i
.
i
2 3
3
8.
п.2. Вычисление несобственныхинтегралов от рациональных
функций.
Рассмотрим интеграл вида
f ( x)dx,
где f (x) — рациональная функция.
9.
Теорема 1.Пусть рациональная функция
P( x)
f ( x)
Q( x)
не имеет полюсов на действительной оси,
причем степень n многочлена Q(x) , по
крайней мере на 2 превышает степень m
многочлена P (x ) , т.е. n m 2.
Тогда
N
f ( x)dx 2 i res f ( z),
k 1
z zk
где z k — все различные полюсы функции f (x),
лежащие в верхней полуплоскости Im z 0.
10.
Доказательство.Из определения несобственного интеграла 1го рода следует, что
R
f ( x)dx lim
R
f ( x)dx.
R
Рассмотрим следующий замкнутый контур:
CR [ R, R],
y
где
CR
CR {z : | z | R, Im z 0}.
–R
0
R
x
11.
Заметим, что функция f (x) может иметь лишьконечное число полюсов, так как знаменатель
Q(x) имеет конечное число нулей.
Выберем радиус R настолько большим, чтобы
все полюсы z1, z2 ,..., z N функции f (x) ,
лежащие в верхней полуплоскости,
заключались внутри контура Г.
y
CR
–R
Тогда
N
z1
f ( z)dz 2 i res f ( z)
zN
0
R
x
k 1
z zk
12.
илиR
N
f ( x)dx f ( z)dz 2 i res f ( z).
R
Покажем, что
k 1
CR
z zk
lim f ( z )dz 0.
R
(1)
a0
Действительно,
1
...
am z m
am z m
P( z ) am z m ... a0
| f ( z ) |
Q( z )
bn z n ... b0
bn z n 1 ... b0
n
bn z
a0
1 ...
am
am z m
.
bn z n m 1 ... b0
n
bn z
CR
13.
Поэтому, при n m 2 и достаточнобольших | z | R будем иметь
2 | am |
A
| bn | R
2 | am |
A
.
| bn |
R
| f ( z ) |
где
2
,
2
Значит, при R
A
A
C f ( z)dz C | f ( z) | | dz | R2 R R 0.
R
R
14.
Следовательно, переходя в равенстве (1) кпределу при R
R
N
lim f ( x)dx lim f ( z )dz lim 2 i res f ( z ),
R
R
R
R
CR
k 1
получим
N
k 1
f ( x)dx 2 i res f ( z).
z zk
z zk
15.
Пример 2. Вычислить интегралdx
.
4
x
1
Решение. Функция
f ( z)
1
z 1
4
очевидно, удовлетворяет условиям теоремы 1.
Найдем особые точки
z 1 0,
4
zk
2 k
i
e 4 , k 0,3 — простые
полюсы.
16.
В верхней полуплоскости находятся:i
4
2
2
z0 e
i
, z1 e
2
2
Поэтому,
3
i
4
2
2
i
.
2
2
dx
2
i
res
f
(
z
)
res
f
(
z
)
4
x 1
z z0
z z1
1
1 i z0 z1
2 i 3 3 4 4
4z0 4z1 2 z0 z1
i
2
2i
.
2
2
2
17.
п.3. Вычисление несобственныхинтегралов вида
f ( x) cos xdx, f ( x)sin xdx, 0.
Лемма 1. (Жордана)
Пусть функция f ( z ) является аналитической в
верхней полуплоскости Im z 0 , за исключением
конечного числа изолированных особых точек, и
равномерно относительно arg z,0 arg z ,
стремится к нулю при | z | .
Тогда при 0
lim f ( z )ei z dz 0,
R
R
C {z : | z | R, Im z 0}.
CR
18.
Доказательство.Сделаем замену
i
i
z R e , dz iR e d , [0, ].
Тогда
f ( z)e dz f ( R e )e
i z
CR
i
i R (cos i sin )
i
iR e d
0
0
i
f ( R e )e
i R cos R sin
e
i
iR e d
19.
if (R e ) e
R sin
Rd .
0
По условию леммы
i
max f ( R e ) ( R) 0 при R .
0
Поэтому
f ( z)e dz R ( R) e
i z
CR
0
R sin
d .
(3)
20.
Преобразуем интеграл в правой части (3):e
R sin
/2
d
0
e
R sin
d
e
R sin
d .
/2
0
Во втором из полученных интегралов положим
t :
e
R sin
0
d e
/2
т.е.
R sin( t )
/2
dt
/2
0
e
R sin
e
R sin t
0
/2
d 2 e
0
R sin
d .
dt ,
21.
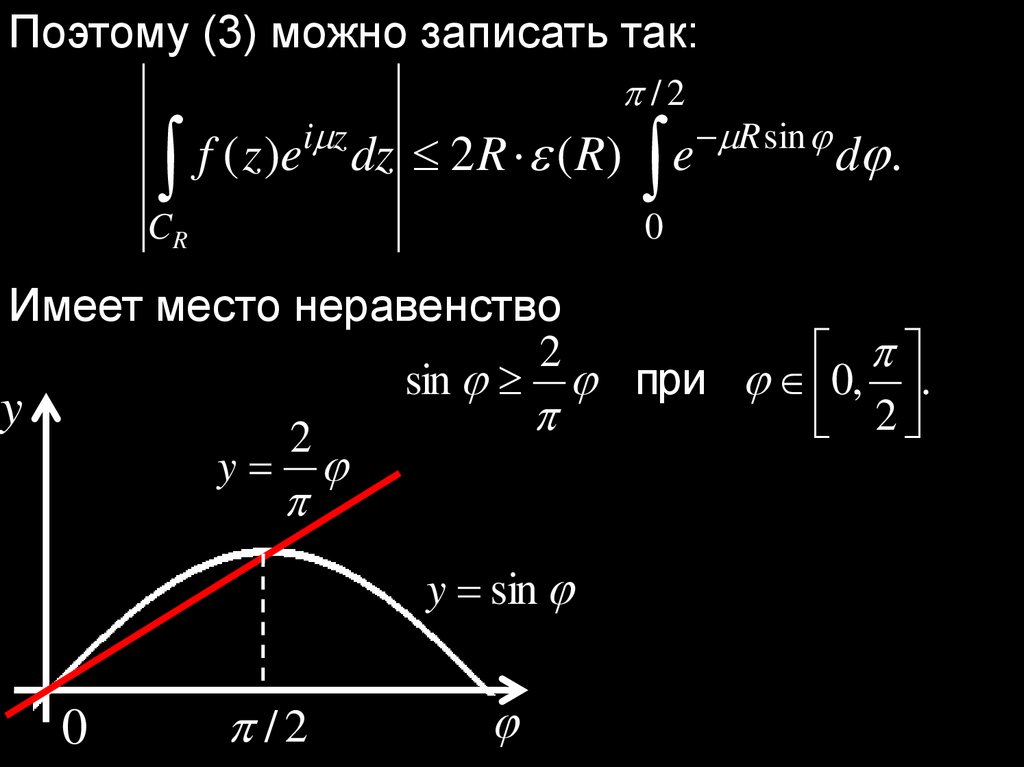
Поэтому (3) можно записать так:/2
i z
f ( z )e dz 2 R ( R)
CR
e
R sin
d .
0
Имеет место неравенство
2
sin при 0, .
y
2
2
y
y sin
0
/2
22.
Значит, при R/2
f ( z)e dz 2R ( R) e
i z
CR
2
R
d
0
2 2
R
( R)
R
e
1 e
2 R ( R)
2 R
( R)
0.
0
23.
Теорема 2.Пусть функция f ( z ) аналитична в замкнутой
верхней полуплоскости Im z 0 , за
исключением конечного числа особых
точек z1, z2 ,..., z N , расположенных в открытой
верхней полуплоскости Im z 0 .
Если при этом в замкнутой верхней
полуплоскости f ( z ) 0 при z ,
равномерно относительно arg z,0 arg z ,
при | z | , то для любого 0 справедлива
формула
N
i x
i z
f ( x)e dx 2 i res f ( z )e . (4)
k 1
z zk
24.
Доказательство данной теоремы аналогичнодоказательство теоремы 1.
Из определения несобственного интеграла
следует, что
R
f ( x)e dx lim f ( x)e dx.
i x
R
i x
R
Отметим также, что все особые точки
i z
функции f ( z )e совпадают с особыми
точками функции f ( z ).
В качестве контура интегрирования возьмем
тот же контур Г, что и в теореме 1.
25.
Выберем радиус R настолько большим, чтобывсе точки z1, z2 ,..., z N лежали внутри Г.
Тогда по теореме 1 § 18
R
N
i x
i z
i z
f
(
x
)
e
dx
f
(
z
)
e
dz
2
i
res
f
(
z
)
e
. (5)
R
k 1
CR
z zk
Воспользовавшись леммой Жордана, получим
lim f ( z )e dz 0.
i z
R
CR
26.
Следовательно, переходя в равенстве (5) кпределу при R
R
N
lim f ( x)ei x dx lim f ( z )ei z dz lim 2 i res f ( z )ei z ,
R
R
R
R
CR
k 1
z zk
получим
N
f ( x)e dx 2 i res f ( z)e .
i x
k 1
i z
z zk
27.
Замечание 1.Формулу (4) можно записать в виде:
i x
i x
i z
f
(
x
)
e
f
(
x
)
e
dx
2
i
res
f
(
z
)
e
. (6)
N
k 1
0
z zk
Доказательство. Так как
0
0
0
i x
i t
i t
f
(
x
)
e
dx
x
t
f
(
t
)
e
dt
f
(
t
)
e
dt ,
то
0
0
0
i x
i x
i x
i x
f
(
x
)
e
f
(
x
)
e
dx
f
(
x
)
e
dx
f
(
x
)
e
dx
f ( x)e dx.
i x
28.
Замечание 2.Если f (x) — четная функция, то формула (6)
принимает вид:
N
0
k 1
f ( x) cos xdx i res f ( z)e .
i z
z zk
Если f (x) — нечетная функция, то формула
(6) принимает вид:
N
0
k 1
f ( x)sin xdx res f ( z)e .
i z
z zk
29.
Пример 3. Вычислить интегралI
cos x
x2 a
dx
,
0
,
a
0
.
2
0
Решение. Функция
f ( z)
1
z a
2
2
удовлетворяет всем условиям леммы
Жордана, является четной и имеет в верхней
полуплоскости одну особую точку
z1 ia — простой полюс.
30.
Поэтому,i z
e
i z
I i res f ( z )e i res 2 2
z z1
z ia z a
i z
e
i
2z
a
z ia
a
e
e
i
.
2ia
2a
31.
Пример 4. Вычислить интегралI
x sin x
x2 a
dx
,
0
,
a
0
.
2
0
Решение. Функция
f ( z)
z
z a
2
2
удовлетворяет всем условиям леммы
Жордана, является нечетной и имеет в
верхней полуплоскости одну особую точку
z1 ia — простой полюс.
32.
Поэтому,I res f ( z )e
z z1
i z
ze
2z
i z
i z
ze
res 2 2
z ia z a
a
z ia
a
iae
e
2ia
2
.

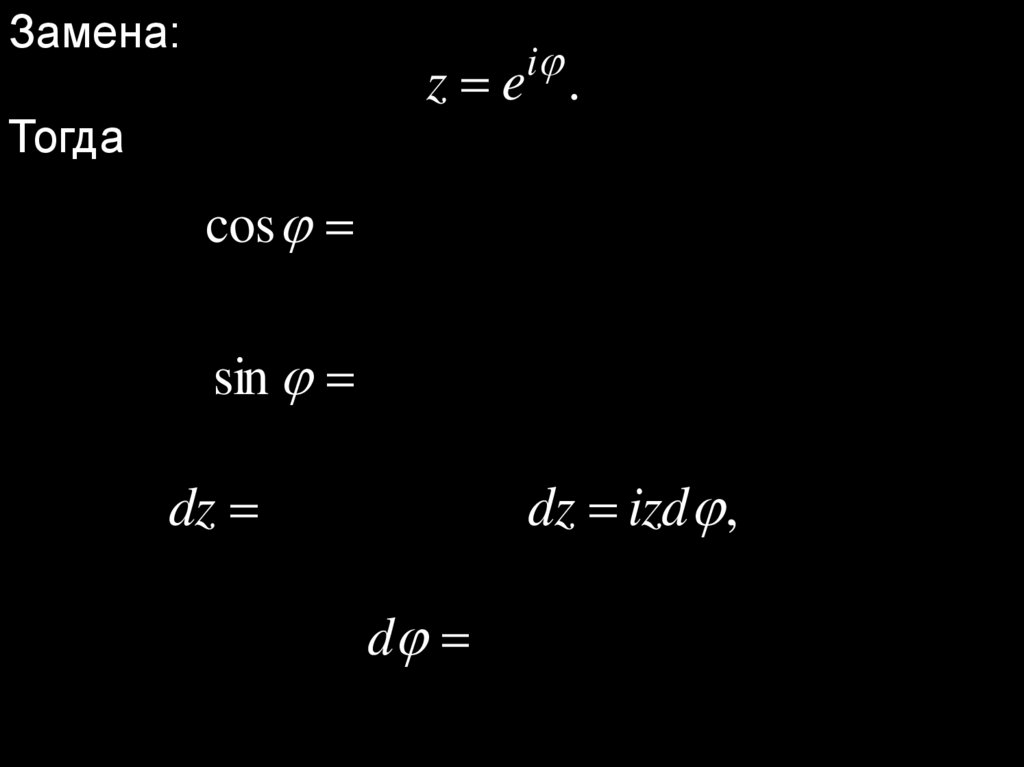









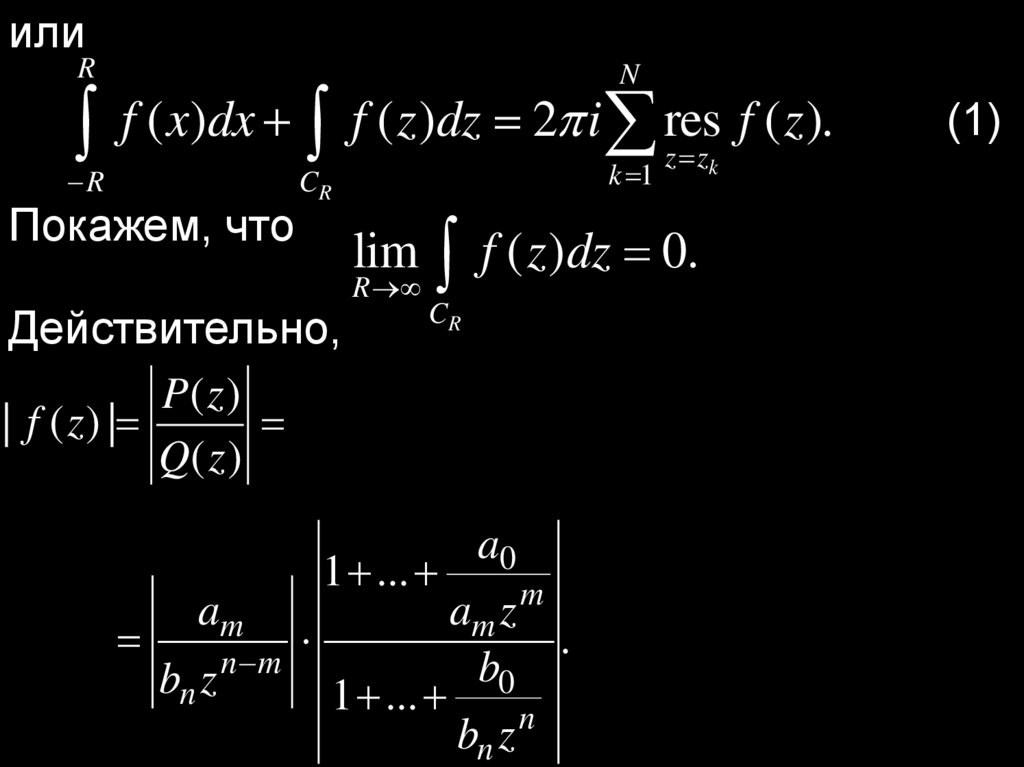






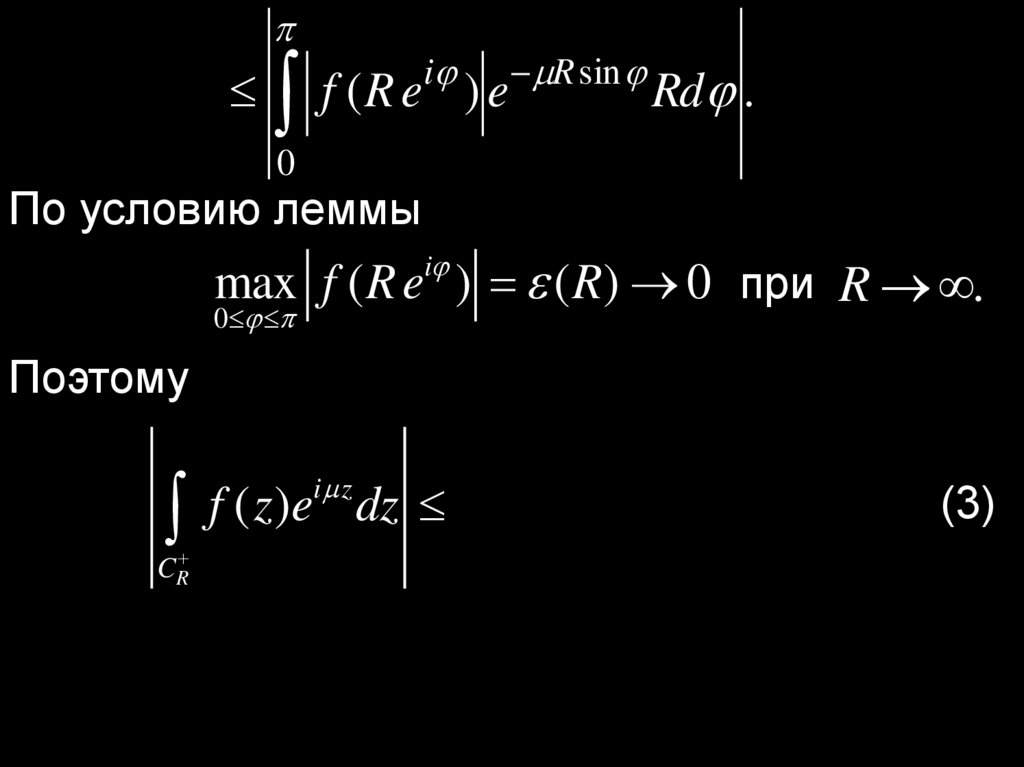

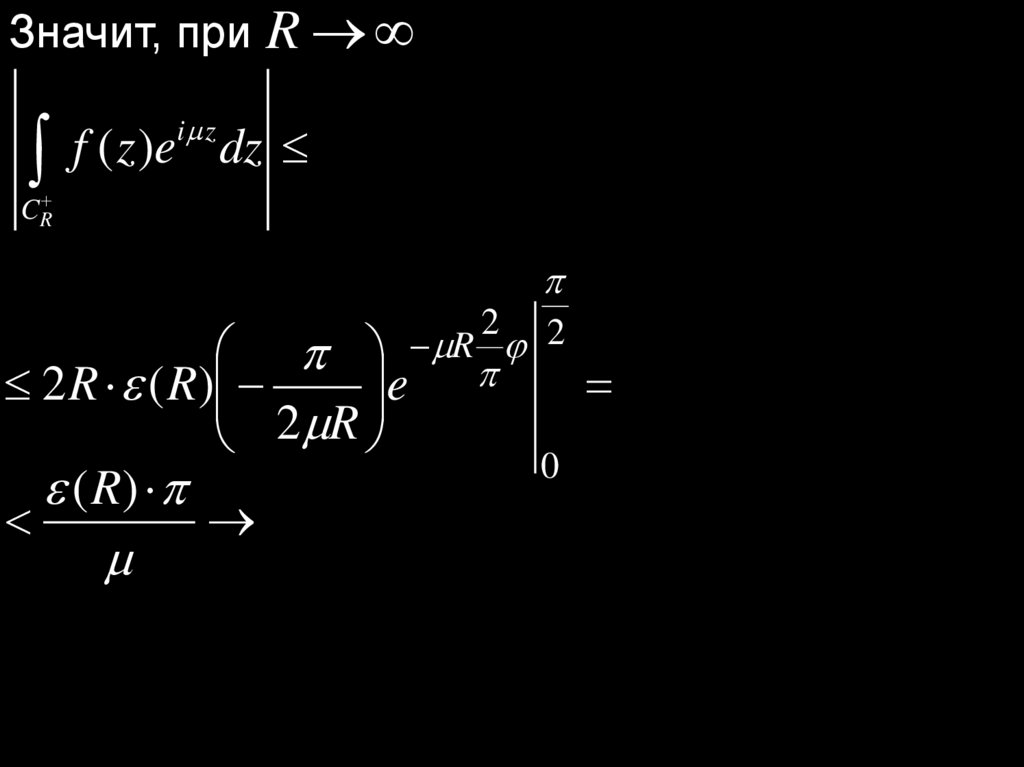







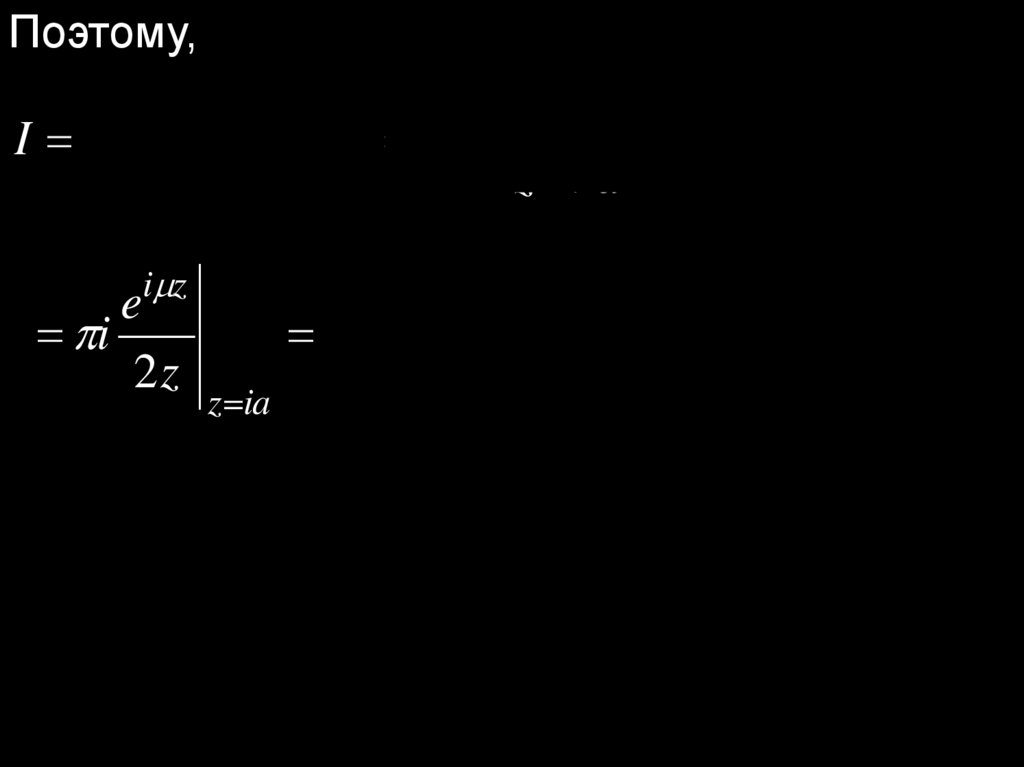

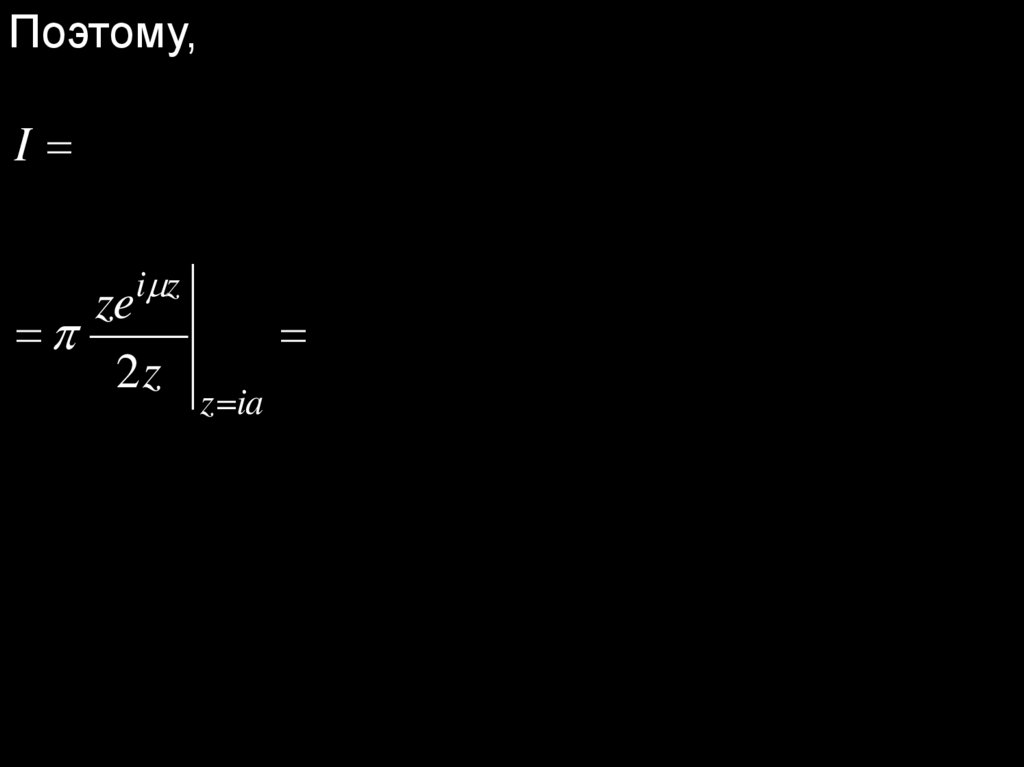
 Математика
Математика








