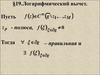Вычет, нахождение вычета. Лекция 34

1.

Лекция 34. Вычет, нахождение вычета.
Теорема Коши о вычетах, вычет в
бесконечно удаленной точке. Применение
вычетов к вычислению контурных и
несобственных интегралов от функции
действительного переменного.

2.

Определение вычетов.
Пусть f ( z ) - аналитическая функция в области 0 z z 0 R ,
R – действительное число > 0
Вычетом f ( z ) в этой области называется число обозначаемое
def
1
Выч f ( z )
f ( z )dz
z z0
2 i L
L-контур, ориентированный против часовой стрелки, области,
произвольной, содержащей внутри себя точку z 0 .
В данном случае точка z 0 - конечная, т.е. z 0
Встречается обозначение:
res f ( z ) Выч f ( z ) .
z z0
z z0

3.

Вычисление вычетов.
Пусть z 0 – устранимая, особая точка функции f ( z ) . Покажем, что
вычет функции f ( z ) в точке z z 0 0 .
Так как z 0 – устранимая особая точка, то в разложении функции в ряд
Лорана присутствует только правильная часть.
f ( z ) a n ( z z 0 )n
n 0
1
n
a
(
z
z
)
dz
n
0
z z0
2 i n 0
Ряд Лорана равномерно сходится, его можно почленно интегрировать
1
a n ( z z 0 ) n dz 0
2 i n 0 L
0
Пусть точка z 0 - полюс первого порядка. В этой точке разложение
функции в ряд Лорана имеет вид:
a 1
n
f ( z ) an ( z z0 )
z z0
n 0
Рассматриваемый
ряд
Лорана
сходится
равномерно
на
рассматриваемой области.
Выч f ( z )

4.

Поэтому:
1
dz
n
Выч f ( z )
a
(
z
z
)
dz
a
n
0
z z 1
z z0
2 i n 0 L
0
L
0
2πi
Выч f ( z ) a 1
z z0
Вычет функции в случае полюса первого порядка равен коэффициенту
главной части разложения функции в ряд Лорана.
Пусть z 0 полюс m-того порядка.
Тогда f ( z ) представима в виде:
a m
a
a 2
f ( z ) an ( z z 0 )n 1
...
z z 0 ( z z 0 )2
( z z 0 )m
n 0
Тогда вычет равен:
m
1
dz
dz
n
Выч f ( z )
a k
a 1
a n ( z z 0 ) dz a 1
k
z z0
2 i n 0 L
z
z
(
z
z
)
k
2
0
L
L
0
0
2πi
0
Выч f ( z ) a 1
z z0
В случае m-того порядка вычет равен первому коэффициенту
разложения функции в ряд Лорана в окрестности особой точки.
Пусть z 0 - существенно особая точка.
Выч f ( z ) a 1
z z0
Одним из основных способов нахождения вычетов является способ
определения коэффициентов главной части в окрестности особой точки.

5.

Вычисление вычетов в случае простого полюса и полюса m-того порядка
Пусть т. z 0 - полюс первого порядка. Тогда функция f ( z ) представима
в виде:
a
f ( z ) a n ( z z 0 )n 1
z z0
n 0
Умножим все выражения на ( z z 0 ) получим:
a 1 f ( z )( z z 0 ) a n ( z z 0 ) n 1
n 0
Перейдем к пределу, при z z 0
a 1 lim f ( z )( z z 0 ) lim a n ( z z 0 ) n 1
z z0 n 0
z z0
0
Ряд равномерно сходится, поэтому возможен предельный переход под
знаком ряда. А, следовательно, ряд равен 0.
Выч f ( z ) a 1 lim f ( z )( z z 0 )
z z0
z z0

6.

Замечание: если f ( z ) имеет в точке z 0 полюс первого порядка и
представима в виде
( z )
,
f(z)
( z )
где
( z 0 ) 0
( z 0 ) 0
z 0 - нуль 1-го порядка функции ( z0 ) , но ' ( z 0 ) 0 .
Тогда:
( z ) ( z0 )
z z0 ( z )
' ( z0 )
Выч
Доказательство:
( z )
( z )
lim
( z z0 )
z z0 ' ( z )
z z0 ( z )
Выч

7.

По условию ( z0 ) 0 . Тогда
( z )
( z ) ( z0 )
( z )
Выч
lim
*
z z0
z z0 ( z )
z z0
т.к. предел числителя и знаменателя , и предел знаменателя равен
производной, то
( z 0 )
*
' ( z 0 )
Пусть z 0 полюс m-того порядка. Функция представима в виде:
a n
a
a 2
f ( z ) an ( z z 0 )n 1
...
z z 0 ( z z 0 )2
( z z 0 )n
n 0
Выч f ( z ) a 1
z z0

8.

Умножим обе части разложения на ( z z 0 ) m :
( z z0 ) f ( z ) an ( z z0 ) n m a 1 ( z z0 ) m 1 a 2 ( z z0 ) m 2 ... a m
m
n 0
d m 1
m
n 1
(
z
z
)
f
(
z
)
a
(
n
m
)(
n
m
1
)(
n
2
)(
z
z
)
0
n
0
m 1
dz
n 0
an 1 (m 1)(m 2) ... 2 1 0
( m 1 )!
В полученном выражении перейдем к пределу при z z 0 , используя
свойство равномерно сходящихся рядов:
d m 1
lim m 1 ( z z 0 )m f ( z ) ( m 1 )! a 1
z z0 dz
1
d m 1
Выч f ( z )
lim m 1 ( z z 0 ) m f ( z )
z z0
( m 1 )! z z0 dz
Если полюс m-того порядка.

9.

Определение характера особых точек и вычетов этих особых точек.
1 ez
Пусть дана f ( z ) 5
z
Особой точкой является точка z 0 0 , так как в этой точке происходит
нарушение аналитичности (знаменатель обращается в ноль).
Определяем характер особой точки. Для этого функцию e z разложим в
ряд:
2
3
4
5
6
z
z
z
z
z
1 e z 1 1 z
...
2! 3! 4! 5! 6!
Функция f ( z ) в окрестности точки z 0 может быть представима в виде:
z2 z3 z4 z5 z6
1 1 z
...
1 ez
2
!
3
!
4
!
5
!
6
!
f(z)
5
5
z
z
1
1 1 1 1
1 1 1 1
4
z ...
3
2
2! z
3! z
4! z 5! 6!
z
главная часть правильная часть ряда Лорана
Особая точка z 0 - полюс 4-го порядка.

10.

1 ez
Найдем вычет функции
z5
1 ez
1
1
Выч 5 a 1
z 0
4!
24
z
1
Пример: f ( z )
2
1 ez
z0 = 0 – особая точка.
Найдем характер особой точки.
4
6
2
4
6
2
z
z
z
z
z
z
2
2
1 e 1 1 z
... z 1
...
2! 3!
2! 3! 4!
(z)
1
1
f(z)
, ( z0 ) 0
2
z2
z ( z )
1 e
Точка z0 = 0 – полюс 2-го порядка. Найдем вычет для этой функции.

11.

2
2
1
d 2 1
2 z( 1 e z ) z 2 ( 2 z )e z
0
Выч f ( z ) lim
z
lim
2
z2 2
z0 0
1! z 0 dz 1 e z z 0
0
(1 e )
z2
2z e ( 2z 2z ) 0
lim
4
z 0
0 z 0
z
lim
z2
lim
3
2 e ( 4z 4z 6z 2 )
4
z 0
2
4z
z 0
12 z 2
e – 1 ~
z2
lim
lim
ez
3
4
z2
2
12 z
2
2
z 0 12
( 8 z 3 20 z ) 0
2
e z 1 ~ z 2
1
f ( z ) ez
Пусть дана функция
Особая точка z0 = 0. Разложение функции имеет вид
1
1
1
ez 1
...
z 0
2
z 2! z
существенно особая точка
1
Выч e z 1
z 0
2 ze ( 4 z 2 z 2 ) e ( 16 z 3 4 z )
z 0
2
lim
2
4z
2
3
e z ( 8 z 5 20 z 3 )
2
2 2 ze z ( 2 z 3 2 z ) e z ( 6 z 2 2 )

12.

Применение вычетов к вычислению интегралов по замкнутому контуру
Теорема (основная теорема о вычетах) Если f (z) аналитична в
замкнутой области D c границей Г, за исключением конечного числа особых
k
точек z1, z2, …, zk D. Тогда: f ( z )dz 2 i Выч f ( z )
Г
n 1 z zm
у
g2 g1
z2
z3
O
z
z1
zk
x
g3 gk
Окружим точки контурами g1,g2,g3, ориентированными как и контур Г.
В области D с вырезами функция f (z) аналитична.
Используя формулировку теоремы Коши для многосвязной области:
k
f ( z )dz f ( z )dz
Г
n 1 g п
Левую и правую части делим на 2πi
k 1
1
f ( z )dz 2 i f ( z )dz – вычеты f (z) в точке zn по определению,
2 i Г
n 1
gп
k
тогда: f ( z )dz 2 i Выч f ( z )
Г
n 1 z z n

13.

Пример:
ez
z 2 z 1
ez
ez
2
dz
2
i
Âû÷
2
i
1
1
1
z
z 1 z
1
(
z
2
)
z
( z 2)
2
z
2
2
2
1
e2
1
4 2
2 i
ie
3
3
2

14.

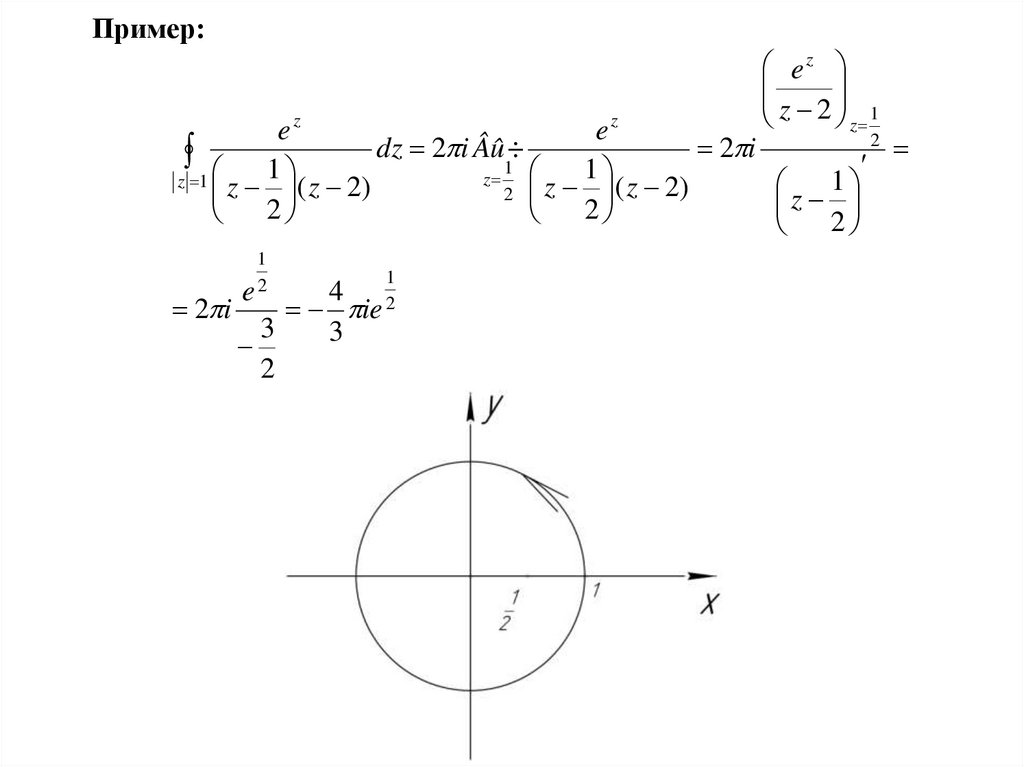
Вычисление определенных интегралов с помощью вычетов
Покажем, что интеграл вида
2
R(sin ,cos )d с помощью подстановки z e
i
можно перевести в
0
интеграл
*
*
R
(sin
,
cos
)
R
(
z
)
dz
,
где
рациональная
функция,
R
(z) –
z 1
рациональная функция.
Так как z e i => dz = iei dz => d =
e i e i
1
1
sin
sin z
2i
2i
z
e i e i
1
1
cos
cos z
2
2
z
С учетом подстановки
dz
i
dz
i
z
ie

15.

i
z e ,0 2 , z 1
2
1
1
R(sin ,cos )d cos 2 z z
0
sin 1 z 1
2i
z
1 1
1 i
1
R z , z dz
2 2i
z z
z 1 2

16.

В результате замены интеграл переходит в интеграл вида:
n
i 1
i 1
1 1
1
1 1
1
R z , z dz 2 i Âû÷ R z , z ;
z 2i
z
z 2i
z
i 1 z zi z 2
z 1 z 2
Формула для вычисления любого интеграла.
Вычисление интегралов вида f ( x )dx с помощью вычетов.
Теорема. Если функция комплексного переменного f (z) аналитична в
верхней полуплоскости Im z 0 , и такова что:
M
1. f ( z ) 2 , для | z | R > 0, M = const (верхняя полуплоскость)
z
2. f (z) имеет конечное число особых точек в области Im 0, z R
n
k 1 z zk
Тогда f ( x )dx 2 i Выч f ( z )
z1, z2, zm - особые точки области Im 0, z R

17.

Доказательство:
На комплексной плоскости рассмотрим область Im z 0, z R , внутри
которой лежат особые точки нашей функции. Область ориентированная. В
соответствии с теоремой о вычетах:
n
f ( z)
f ( z )dz 2 i Âû÷
z z
k 1
k
Интеграл по замкнутому кругу можно записать:

18.

R
f ( z )dz f ( x )dx
z R
R
R
n
f(z)
f ( x )dx f ( z )dz 2 i Выч
z z
R
k 1
z R
k
Покажем, что при R , 2-ое слагаемое в сумме обращается в 0.
M
M
M R M
i
f
(
z
)
dz
f
(
z
)
dz
dz
dz
R
(
e
)
d
2
2
2
2
R
R z R
R 0
R
z R
z R
z R z
M
lim
R
f ( z )dz 0
z R
Переходя к пределу в выражении
R
n
f ( z ) , R
f ( x )dx f ( z )dz 2 i Выч
z z
R
z R
k 1
k
0
Тогда в результате предельного перехода при R , из равенства
получаем
n
k 1
f(z)
f ( x )dx 2 i Выч
z z
k

19.

dx
2
3
( x 1)
1
Рассмотрим функцию f ( z ) 2
( z 1 )3
dx
1
1
,
Тогда
f
(
z
)
( x 2 1 )3 2 i Выч
z zk ( z 2 1 )3
( z i )3 ( z i )3
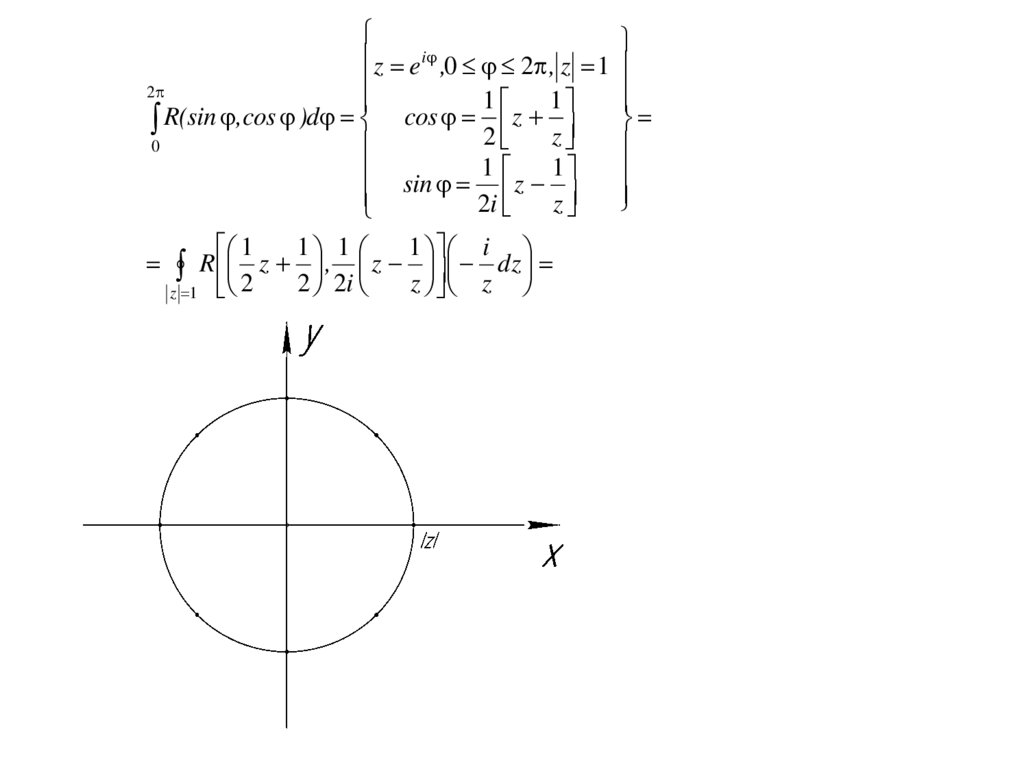
Пример: Найти интеграл
Точка i – полюс 3-го порядка
dx
1
1
d2
1
3
2
i
Выч
2
i
lim
(
z
i
)
( x 2 1 )3
3
3
z i ( z 2 1 )3
z i dz 2
(
3
1
)!
(
z
i
)
(
z
i
)
12
12 3
i
z i ( z i )5
32i 5 8
i lim

20.

Применение теории вычетов к интегралам e i x f ( x)dx , > 0.
Теорема: Пусть функция f (z) регулярна в верхней полуплоскости Im z 0 и
такова что:
M
1. f ( z )
, для | z | R > 0
z
2. f (z) имеет в верхней полуплоскости конечное число особых точек z1,…, zn.
n
Тогда f ( x)e dx 2 i Âû÷ f ( z )ei z , > 0
i x
k 1 z zk
n
i z
f
(
x
)
cos
xdx
Im
2
Âû÷
f
(
z
)
e
z zk
,
k 1
n
i z
f
(
x
)
sin
xdx
Re
2
Выч
f
(
z
)
e
z zk
, > 0
k 1
Замечание: Если < 0 все формулы остаются правильными с
точностью до знака, только вычеты нужно искать по особым точкам
лежащим в нижней полуплоскости Im < 0.