Дифференциальные уравнения. Общие сведения о ДУ

1.

2.

10. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
10.1. Общие сведения о ДУ
10.2. Обыкновенные ДУ 1-го порядка
10.3. ДУ с разделяющимися переменными
10.4. Линейные ДУ
10.5. Обыкновенные ДУ 2-го порядка
10.6. ЛОДУ 2-го порядка

3.

10.1. ОБЩИЕ СВЕДЕНИЯ О ДУ
Уравнение называется дифференциальным, если оно связывает
независимую переменную, искомую функцию и её производные, т.е.
F x, y, y , y ,..., y n 0
Решением ДУ называется функция, которая при подстановке в это
ДУ обращает его в тождество.
Если искомая функция зависит от одной переменной,
то ДУ называется обыкновенным.
Если искомая функция зависит от двух или более переменных,
то ДУ называется в частных производных.
Наивысший порядок производной, входящей в ДУ, называется
порядком ДУ.

4.

10.1. ОБЩИЕ СВЕДЕНИЯ О ДУ
Примеры
Определите название ДУ и его порядок.
1)
4 x 2 y 3 xy y 0 – обыкновенное ДУ 4-го порядка
2)
3)
xy y sin x y 2
xz y yz x 0
– обыкновенное ДУ 1-го порядка
– ДУ в частных производных 1-го порядка
Процесс отыскания решения ДУ называется интегрированием.
График решения называется интегральной кривой.

5.

10.2. ОБЫКНОВЕННЫЕ ДУ 1-ГО ПОРЯДКА
Уравнение, которое связывает независимую переменную х,
искомую функцию y = f(x) и её первую производную у ,
называется ДУ 1-го порядка.
F x, y , y 0
Если это ДУ записано в виде
y f x, y ,
то оно называется разрешённым относительно производной.
P x, y dx Q x, y dy 0
– дифференциальная
форма записи ДУ.
Пример
Представить все возможные формы записи ДУ.
e x y y 4 x 4 3 0

6.

10.2. ОБЫКНОВЕННЫЕ ДУ 1-ГО ПОРЯДКА
Задача
Найти все решения ДУ
y x, так как 1
x
;
x
y
y
x
y 3 x, так как 3
3x
;
x
y c x, так как c
c x
x
Начальным условием ДУ называется условие, когда для заданного
значения х=хₒ функция y принимает значение у=уₒ.
Обозначение:
y x0 y0
Общим решением ДУ 1-го порядка называется функция y x, c ,
содержащая одну произвольную постоянную и удовлетворяющая
условиям:
1) y x, c
решение ДУ при каждом фиксированном значении с;
2) для любого начального условия
y x0 y0
существует единственное значение постоянной с=сₒ такое, что
функция
y x, c0 удовлетворяет этому начальному условию.

7.

10.2. ОБЫКНОВЕННЫЕ ДУ 1-ГО ПОРЯДКА
Частным решением ДУ 1-го порядка называется функция y x, c0 ,
полученная из общего решения при конкретном значении постоянной с=сₒ.
Общее решение ДУ есть множество всех его частных решений.
Замечание
Если общее решение получено в неявном виде
то оно называется общим интегралом ДУ,
а частное решение
x, y, c 0,
x, y, c0 0 – частным интегралом.
Задачей Коши называется задача отыскания решения ДУ,
удовлетворяющего заданным начальным условиям.
F x, y, y 0,
y x0 y0 .

8.

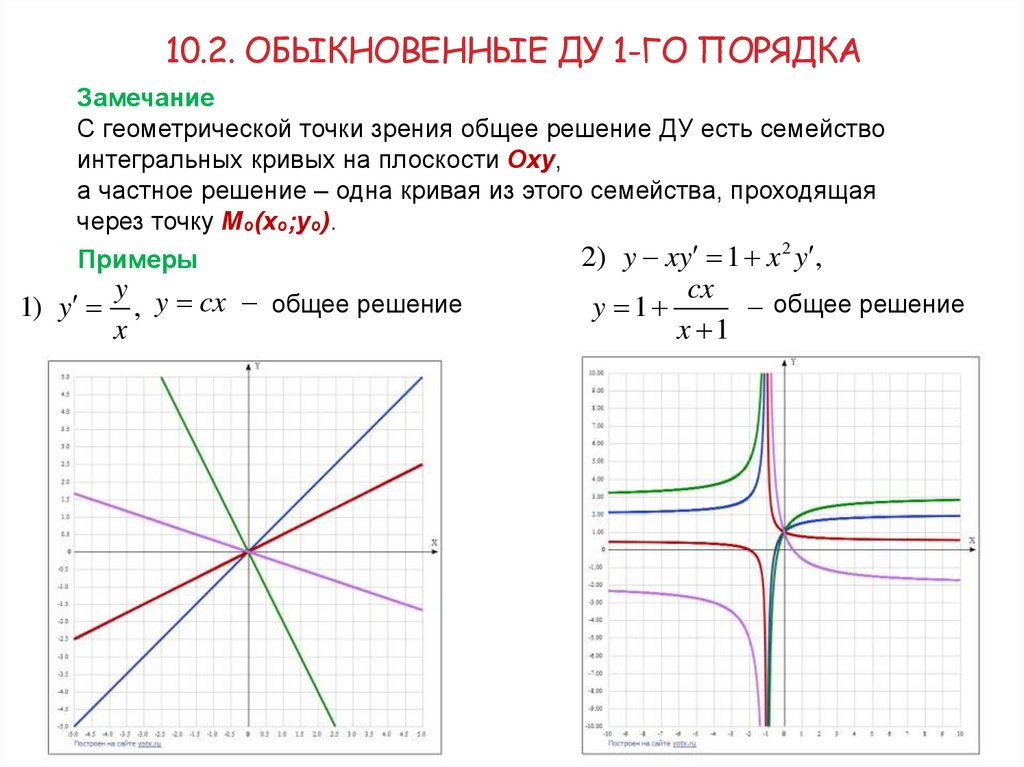
10.2. ОБЫКНОВЕННЫЕ ДУ 1-ГО ПОРЯДКА
Замечание
С геометрической точки зрения общее решение ДУ есть семейство
интегральных кривых на плоскости Оху,
а частное решение – одна кривая из этого семейства, проходящая
через точку Мₒ(хₒ;уₒ).
2) y xy 1 x 2 y ,
Примеры
1) y
y y cx
общее решение
,
x
y 1
cx
общее решение
x 1

9.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Уравнение вида P x dx Q y dy
называется ДУ с разделёнными переменными.
Способ решения:
проинтегрировать обе части, добавить постоянную с.
Примеры
Найти общее решение или общий интеграл ДУ.
2) sin xdx cos ydy 0
sin xdx cos ydy
1) x 2 dx ydy
2
x
dx ydy
x3 y 2
c
3
2
3
x
2
y 2 c
3
2 x3
y
2c
3
общий интеграл
sin xdx cos ydy
cos x sin y c
cos x sin y c
общий интеграл
общее решение

10.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
y dy
Уравнение вида P1 x Q1 y dx P2 x Q2
называется ДУ с разделяющимися переменными.
Способ решения:
разделить переменные, проинтегрировать обе части,
добавить постоянную с.
Разделим обе части уравнения на произведение
P1 x Q1 y
P2 x Q2 y
dx
dy
P2 x Q1 y
P2 x Q1 y
P1 x
Q2 y
dx
dy,
P2 x
Q1 y
тогда
пусть
P2 x Q1 y 0
P1 x
Q2 y
P x ,
Q y ,
P2 x
Q1 y
P x dx Q y dy
ДУ с разделёнными переменными

11.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Пример
Найти общее решение или общий интеграл ДУ.
xy 2 dx 1 x 2 y 4 1 dy
y 2 1 x 2 0
1 x y 1
xy
dx
dy
y 1 x
y 1 x
2 1
x
t ( 2 x)dt y y 2 dy
2
2
2
2
2
4
2
x
y4 1
dx
dy
2
2
1 x
y
x
y4 1
1 x 2 dx y 2 dy
t 1 x 2
2 1
dt 2 xdx y 2 dy
y
dt
dx
2 x
1 1
y3 1
dt
2 t
3 y
1
y3 1
ln t c
2
3 y
3
1
y
1
2
ln x 1 c
2
3 y
общий интеграл

12.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Замечание
Уравнение вида y f x g y
также является ДУ с разделяющимися переменными.
Способ решения:
тот же (разделить переменные, проинтегрировать обе
части, добавить постоянную с).
dy
Представим производную в виде y
dx
Умножим обе части уравнения на dx
Разделим обе части уравнения на g
dy
f x dx,
g y
тогда
пусть
y
dy
f x g y
dx
dy f x g y dx
f x g y
dy
dx
g y
g y
1
Q y ,
g y
Q y dy f x dx
ДУ с разделёнными переменными

13.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Пример
Найти общее решение или общий интеграл ДУ.
y y cos3 x
dy
y cos3 x
dx
dy y cos3xdx
dy
cos3 xdx
y
dx
y 0
t 3 x
dy
y cos3xdx, dt 3dx
1
dx dt
3
1
ln y cos tdt
3
1
ln y sin 3 x c
3
общий интеграл
1
ln y sin 3 x ln c
3
ln y ln e
1
sin 3 x
3
ln c
1
sin 3 x
3
ln y ln c e
y c e
1
sin 3 x
3
общее решение

14.

10.3. ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Пример
Найти решение задачи Коши.
x
x
1
e
yy
e
, y 0 1
dy
x
x
dx
1
e
y
e
dx
1 e ydy e dx
x
x
1 ex 0
ex
ydy
dx
x
x
1 e
t 1 e
ex
x
ydy 1 e x dx, dt e dx
dt
dx x
e
y2
ex
dt
x
2
t e
y2
ln e x 1 c
2
общий интеграл
y 0 1 x0 0, y0 1
12
ln e0 1 c
2
1
1
ln 2 c c ln 2
2
2
y2
1
x
ln e 1 ln 2
2
2
частный интеграл

15.

10.4. ЛИНЕЙНЫЕ ДУ
Уравнение вида y p
x y q x
называется линейным ДУ 1-го порядка.
Замечание 1
Функции p(x) и q(x) зависят только от переменной х,
в частности они могут быть постоянными.
Замечание 2
Иногда сначала нужно преобразовать ДУ, чтобы увидеть форму
записи линейного ДУ из определения.
Способ решения:
ищем решение в виде произведения двух функций
y u x v x (метод Бернулли).

16.

10.4. ЛИНЕЙНЫЕ ДУ
Пример
Найти решение задачи Коши
xy y 3cos3 x
xy y 3cos3 x, y
x 0
y 3
y cos3 x - линейное ДУ, так как
x x
1
.
y p x y q x
1
3
p x , q x cos x
x
x
ищем решение в виде произведения двух функций y u x v x
y u v, y u v u v uv
u v uv
uv 3
cos3x
x x
v 3
u v u v cos3x
x x
пусть выражение в скобках =0
во втором и третьем слагаемых
вынесем u за скобки
v
v x 0,
u v 3 cos3x
x
1
2

17.

1
v
10.4. ЛИНЕЙНЫЕ ДУ
3
2
u v cos3x
x
v
0
x
ДУ с разделяющимися переменными
подставим найденное v и упростим
dv
v
dx
x
v
dv dx
x
dv
dx
v
x
dv
dx
v x
dx
1 3
u cos3 x
x x
u 3cos3 x
v 0
ДУ с разделяющимися переменными
ln v ln x
c 0
1
v
x
du
3cos3 x
dx
dx
du 3cos3xdx
du 3 cos3xdx
u cos tdt
u sin t c
t 3 x
dt
3
dx
1
dx dt
3
u sin 3x c

18.

10.4. ЛИНЕЙНЫЕ ДУ
Вспомним, что мы ищем решение ДУ в виде
произведения двух функций
y u x v x
Подставим найденные функции и получим
y sin 3x c
1
x
общее решение
y
1
1
x0 , y0
sin 3 c
1
1
c 1
y sin 3 x 1
1
x
частное решение

19.

10.5. ОБЫКНОВЕННЫЕ ДУ 2-ГО ПОРЯДКА
F x, y, y , y 0
y f x, y, y
y x
– ДУ 2-го порядка
– ДУ 2-го порядка, разрешённое относительно
старшей производной
– решение ДУ 2-го порядка
y x0 y0 , y x0 y0 – начальные условия
y x, c1 , c2
y x, c10 , c20
x, y, c1 , c2 0
x, y, c10 , c20 0
– общее решение
– частное решение, удовлетворяющее заданным
начальным условиям
– общий интеграл
– частный интеграл
F x, y, y , y 0, y x0 y0 , y x0 y0 – задача Коши
для ДУ 2-го порядка

20.

10.6. ЛОДУ 2-ГО ПОРЯДКА
Уравнение вида a0 x y a1 x y a2 x y 0
называется ЛОДУ 2-го порядка с переменными коэффициентами.
Теорема
Если функции y1 y1
x и y2 y2 x являются частными
решениями ДУ (1), то решением этого ДУ также является функция
y c1 y1 x c2 y2 x , где c1 , c2 const.
Пусть эти два частных решения обладают следующим свойством:
y1
W x
y1
тогда
y2
0,
y2
определитель Вронского
y c1 y1 x c2 y2 x
– общее решение ДУ (1).
(1)

21.

10.6. ЛОДУ 2-ГО ПОРЯДКА
Уравнение вида a0 y a1 y a2 y 0
a0 , a1 , a2 R
называется ЛОДУ 2-го порядка с постоянными коэффициентами.
Будем искать частные решения ДУ (2) в виде
y e kx ,
где число k может быть действительным или комплексным.
y e kx , y ke kx , y k 2e kx
подставим в ДУ (2) и получим
уравнение:
a0 k e a1k e a2 e 0
2
kx
kx
e kx a0 k 2 a1k a2 0
e kx 0 kx
a0 k 2 a1k a2 0
kx
характеристическое уравнение
это квадратное уравнение, его сразу
можно получить из ДУ (2), заменив
(2)

22.

10.6. ЛОДУ 2-ГО ПОРЯДКА
a0 k 2 a1k a2 0
D a1 4a0 a2
2
D>0 два действительных корня
D=0 один действительный корень
кратности 2
D<0 два комплексно-сопряжённых
корня
Пример
Решить квадратное уравнение
k 2 6k 25 0.
D 6 4 1 25 36 100 64 64 1 64i 2 (i – мнимая единица)
2
6 64i 2
6 8i
6 8i
k1,2
3 4i
2
2
2 2
i
= 3 – действительная часть, = 4 – мнимая часть комплексного числа

23.

10.6. ЛОДУ 2-ГО ПОРЯДКА
случай
D
общее решение
ЛОДУ (2)
корни
1
D 0 k1 k2
y c1 e k1x c2 e k2 x
2
D 0 k1 k2 k
y c1 e kx c2 x e kx
3
D 0 k1,2 i
y e x c1 cos x c2 sin x
y c1 y1 x c2 y2 x
– общее решение

24.

10.6. ЛОДУ 2-ГО ПОРЯДКА
Примеры
Решить ЛОДУ 2-го порядка.
1)
y 2 y y 0
k 2 2k 1 0
k 1 0
2
2)
y 2 y 3 y 0
k 2 2k 3 0
D 22 4 1 3 4 12 16
k 1 0
k 1
y c1 e x c2 x e x
y c1 e x c2 e 3 x
общее решение
( см. таблицу, случай 2)
общее решение
( см. таблицу, случай 1)
2 4
2 4
k1
1, k2
3
2
2

25.

10.6. ЛОДУ 2-ГО ПОРЯДКА
Примеры
Решить ЛОДУ 2-го порядка.
3)
y 2 y 2 y 0
k 2 2k 2 0
D 22 4 1 2 4 8 4 4 1 4i 2
2 2i
k1,2
1 i
2
1, 1
y e x c1 cos x c2 sin x
общее решение
( см. таблицу, случай 3)

26.

10.6. ЛОДУ 2-ГО ПОРЯДКА
Примеры
Решить ЛОДУ 2-го порядка (задача Коши).
4)
y 5 y 0, y 0 3, y 0 5
y 5 y 0
подставим начальные условия в
k 2 5k 0
общее решение и его производную:
k k 5 0
5 0
3
c
c
e
, 3 c1 c2 ,
1
2
k1 0, k2 5
0 x
y c1 e c2 e
y c1 c2 e5 x
5x
общее решение
( см. таблицу, случай 1)
найдём производную
общего решения:
y 5c2 e5 x
5 0
5 5c2
5 5c2 e
3 c1 1, c1 2,
c
1
2
c2 1
подставим найденные константы в
общее решение :
y 2 e5 x
частное решение

27.

ЛЕКЦИИ ЗА 2 СЕМЕСТР ЗАВЕРШЕНЫ