Похожие презентации:
Классы интегрируемых функций
1.
Лекция 6Классы интегрируемых функций
1)
Интегрирование рациональных дробей.
2) Интегрирование выражений,
содержащих
тригонометрические функции.
2.
1.Интегрирование рациональных дробей.
Общая схема.
1) Если дробь
fn x
m x
неправильная n m ,
то её представляют в виде суммы целой
Rp x
части и правильной
рациональной
дроби :
fn x
Ql x
.
m x
m x
2) Находят корни знаменателя правильной
рациональной дроби и разлагают его на
квадратичные и линейные множители с
действительными коэффициентами.
3.
3) Записывают разложение полученнойправильной дроби на простейшие.
4) Интегрируют каждую простейшую дробь.
4.
Т Правильную рациональную дробь можноразложить на сумму простейших дробей
четырех типов:
A
A
Bx C
Bx C
,
, 2
,
k
x a x a
x px q x 2 px q
p 4q 0.
2
k
Каждому действительному корню a кратности m
знаменателя m x в разложении соответствует
сумма простейших дробей первых двух типов:
,
5.
AmA1
A2
...
.
2
m
x a x a
x a
Каждой комплексно сопряженной паре корней
кратности m соответствует сумма простейших
дробей третьего и четвёртого типов:
M1 x N 1
M2 x N2
2
2
x px q
x px q
2
...
Mm x Nm
x
2
px q
m
Коэффициенты Ai,Mi,Ni могут быть найдены
после приведения суммы простейших дробей к
общему знаменателю.
.
6.
Способы определения коэффициентов:• Метод неопределённых коэффициентов
(приравнивание коэффициентов при одинаковых
степенях x ).
• Подстановка подходящих чисел в тождество.
Пример.
x
xdx
2
1 x 2
?
Разлагаем правильную дробь на сумму
простейших дробей:
7.
xx 1 x 1 x 2
A
B
C
;
x 1 x 1 x 2
x A x 1 x 2 B x 1 x 2 C x 1 x 1 ;
1
x 1 : 1 2 A, A ;
2
1
x 1 : -1 B 2 3 , B ;
6
2
x 2 : 2 C
1 3, C ;
3
x
1
1
2
.
2
2 x 1 6 x 1 3 x 2
x 1 x 2
8.
По свойству линейности:1 dx 1 dx 2 dx
x 2 1 x 2 2
x 1 6 x 1 3 x 2
xdx
1
1
2
ln x 1 ln x 1 ln x 2 C .
2
6
3
9.
Интегрированиевыражений,
содержащих
2.
тригонометрические функции.
I.
cos n x
sin m xdx
а) n и m – чётные, целые, положительные.
Метод: понижение степени переходом к
двойному аргументу с помощью формул
тригонометрии:
10.
1 cos 2 xcos x
2
1 cos 2 x
2
sin x
2
1
sin x
cos x sin 2 x
2
2
11.
Пример.4
cos
xdx ?
Решение.
2
1 cos 2 x
2
dx
1
1
1
dx
cos 2 xdx
cos 2 2 xdx
4
2
4
4
cos
xdx
x 1
1
sin 2 x
(1 cos 4 x )dx
4 4
8
x 1
x 1
sin 2 x sin 4 x C .
4 4
8 32
12.
б) хотя бы одно из n и m - нечётное, целое,положительное.
Метод:от нечётной степени отделяется один сомножитель
и заносится под знак дифференциала;
оставшаяся подынтегральная функция выражается через
функцию, стоящую под знаком дифференциала при
помощи формулы
sin x cos x 1
2
2
13.
Пример 1:3
5
sin
x
cos
xdx ?
Решение.
sin
3
x cos xdx
5
3
4
sin
x
cos
x
cos xdx
sin x cos xd sin x
3
4
sin x 1 sin x
3
sin x 2sin x sin x d sin x
3
5
7
1 4
1 6
1 8
sin x sin x sin x C .
4
3
8
2
2
d sin x
14.
Пример 2:sin 3 x
dx ?
5
cos x
Решение.
sin 3 x
dx
5
cos x
sin 2 x
sin 2 x
sin xdx 5 d cos x
5
cos x
cos x
1
1
1 cos 2 x
C.
5
d cos x
4
2
4cos x 2cos x
cos x
15.
II .cos x
sin xdx
cos x
cos xdx
sin x
sin xdx
Метод: переход к сумме функций и сумме
интегралов.
При этом используются следующие тригонометрические
формулы:
16.
1sin x
cos x sin( ) x sin( ) x
2
1
cos x
cos x cos( ) x cos( ) x
2
1
sin x
sin x cos( ) x cos( ) x
2
17.
III .R(sin x ,cos x )dx
Здесь R(sin x ,cos x ) рациональная
функция.
Метод - универсальная тригонометрическая
подстановка:
x
t tg
2
18.
xx
x
x
2sin cos
2sin cos
2
2
2
2
sin x
2 x
2 x
2 x
2 x
cos sin
cos
1 tg
2
2
2
2
x
2tg
2t
2
;
2
1
t
2 x
1 tg
2
19.
x2
cos sin
2
cos x
2 x
2
cos sin
2
2
1 t
;
2
1 t
2
2
x cos 2 x
1 tg
2
2
x
2 x
2
cos
1 tg
2
2
x 2arctgt ;
2dt
dx
.
2
1 t
x
2
x
2
20.
Окончательно:2t
sin x
;
2
1 t
2dt
dx
;
2
1 t
1 t
cos x
;
2
1 t
x 2arctg t
2
2t 1 t 2dt
R(sin x ,cos x )dx
R(
,
)
2
2
2
1 t 1 t 1 t
2
(Интеграл приводится к интегралу от
рациональной дроби).
21.
Пример.dx
?
sin x
Решение.
dx
sin x
2dt 1 t
2
x
t tg ;
2
2dt
2t
dx
; sin x
2
2
1 t
1 t
dt
2
t
1 t 2t
x
ln | t | C ln | tg | C .
2
22.
Замечание.Если подынтегральная функция R(sinx,cosx) является
чётной функцией аргументов sinx и cosx, более
эффективной будет подстановка
t tgx
Пример.
dx
dx
2
2
2
2
2
2
2
2
cos x a tg x b
a sin x b cos x
23.
12
a
dx
1
dtgx
2 2 b2 a 2
2
2
b
cos x
tg x 2
tg x 2
a
a
1
dt
2
t tgx
a 2 b 2
t 2
a
1 1
t
1
atgx
2 arctg C
arctg
C.
b
ab
b
a b
a
a




















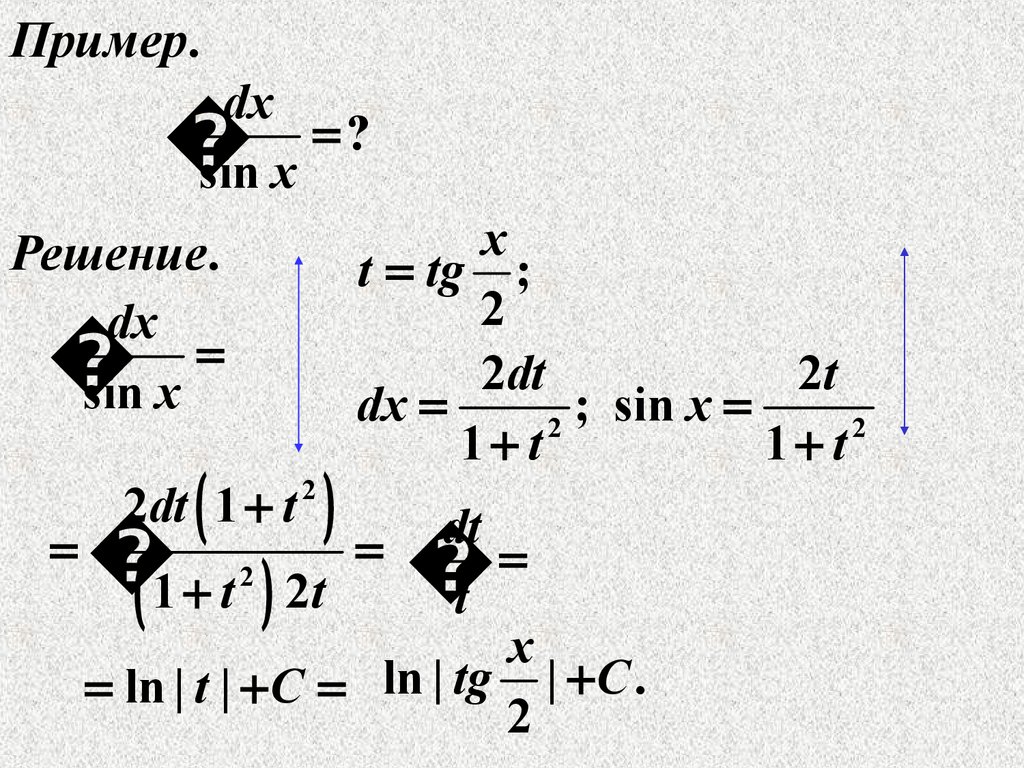


 Математика
Математика








