Похожие презентации:
Первообразная. Первообразные элементарных функций. Правила вычисления первообразных
1.
Первообразная. Первообразныеэлементарных функций. Правила
вычисления первообразных
2.
Устная работа1
сosх
- sinх+12
3.
Устная работа-
4.
При решении задачи, мы, зная производнуюфункции, восстановили ее первичный образ.
Эта операция восстановления - операция
интегрирования.
Восстановленная функция – первообразная
( первичный образ функции)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
5.
Определение первообразнойФункцию F(x) называют
первообразной функции f(x) на
некотором промежутке , если
на нем производная функции
F'(x) = f(x) .
Операцию, обратную
дифференцированию называют
интегрированием
6.
Запомните:+
7.
Функция f(x)K(постоянная)
Первообразная
F(x)
k
Задача:
Найдите все первообразные
для функций:
f(х)=3
f(х)= х2
f(х)=cosx
f(х)=12
f(х)=х5
8.
Таблица первообразныхФункция f (x)
0
x
Первообразная F (x)
1
9.
Три правила нахождения первообразныхЕсли функции у = f(x) и у = g(x) имеют на
промежутке первообразные соответственно
у = F(x) и у = G(x), то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
у =k f(x)
у =k F(x)
10.
Задание № 1.Назовите номера тех
функций, первообразная
которых находится только по
одному из правил:
а) по правилу суммы;
б) по правилу умножения на
постоянный множитель;
в) по правилу сложной
функции.
1. y x x ;
2. y 2 cos x;
3
3. y 8 5 x 10 x ;
2
4. y 4 3 x ;
9
5. y 4sin 3 x;
6. y 4 x.
11.
12.
Неопределенный интеграл.Способы вычисления
13.
14.
Неопределенный интегралСовокупность всех первообразных данной
функции f(x) называется ее неопределенным
интегралом и обозначается
f ( x)dx F ( x) C
,
где C – произвольная постоянная;
f(x) – подынтегральная функция;
F(x) - первообразная
15.
Правила интегрированияcf ( x)dx c f ( x)dx, c const
( f ( x) g ( x))dx f ( x)dx g ( x)dx
1
f (ax b)dx a F (ax b) C , a 0
16.
Свойства интегралаf ( х)dx f ( х)
f
(
x
)
dx
f
(
x
)
С
17.
Таблица неопределенных интегралов1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
18.
Таблица неопределенных интегралов11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
dx
a x
2
arcsin
2
x
C ..
a
16.
dx
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
14.
dx
1
x a
ln
C
2
2
2a x a
x a
19.
dx
thx C .
2
ch x
15.
dx
1
a x
ln
C .
2
2
2a a x
a x
20.
dx
cthx C .
2
sh x
19.
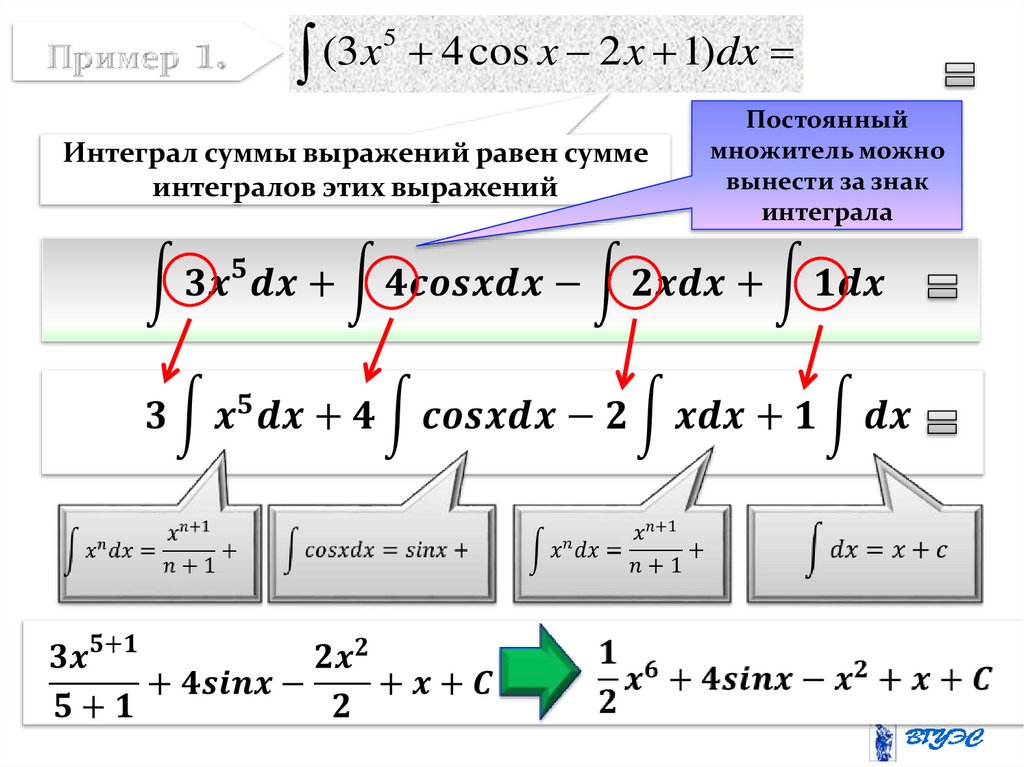
5(
3
x
4 cos x 2 x 1)dx
Интеграл суммы выражений равен сумме
интегралов этих выражений
Постоянный
множитель можно
вынести за знак
интеграла
20.
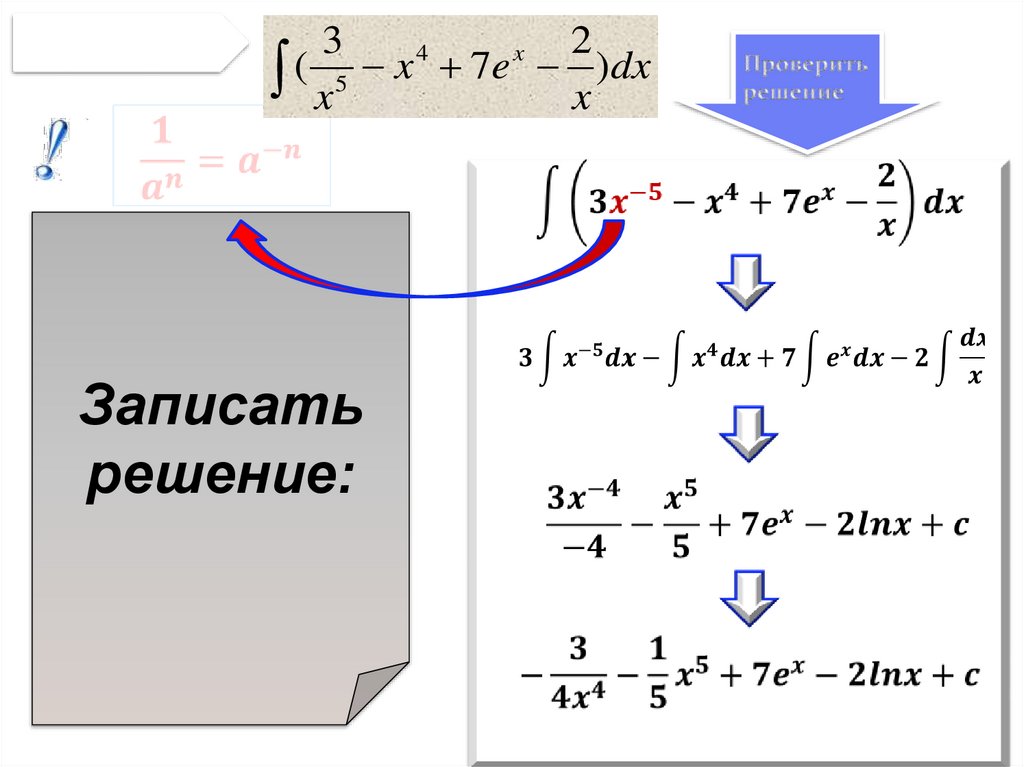
Пример 2.3
2
4
x
( x 5 x 7e x )dx
Записать
решение:
21.
Пример 3.4
3
(
x
3 х ) dx
cos 2 x
Записать
решение:
22.
Cамостоятельная работаНайти неопределенный интеграл
Проверить
решение
Уровень «А» (на «3»)
Уровень «В» (на «4»)
1 65 3 2
1
1). (xх 3x х 44x) dxC
6
2
1
54
33). ((33
44xх)) dx
C
20
2)5 x 3e 4 ln x C
3
1 66xx 3
4). e
dx
4
e
C
6
4
4
х
5
x
2. ( 25 х 3е ) dx
х
Уровень «С» (на «5»)
1
22
3 6
5
sin(55xx 44
) ) dx
C 66).2 ctgx
( 2 x xх 3х5 )dx
C
5). cos(
5
sin 3x
5x




















 Математика
Математика








