Мастер-класс на РМО учителей математики Чесменского района Челябинской области

1.

2.

Формирование
приемов
мыслительной
деятельности
учащихся

3.

Цель мастер-класса: ознакомить
учителей математики с опытом
работы по формированию у
учащихся умения выводить
следствия из заданных условий,
выполнять дедуктивные
умозаключения, делать выводы и
обучению методам доказательства
теорем

4.

Правила вывода
Правило заключения
A B, A
B
Все М есть Р
К есть М
К есть Р
Правило отрицания
A B, B
A
Силлогизм
- большая посылка(БП);
- малая посылка (МП);
- вывод(В).

5.

А
В
A
C
B
D
N
M
E
K
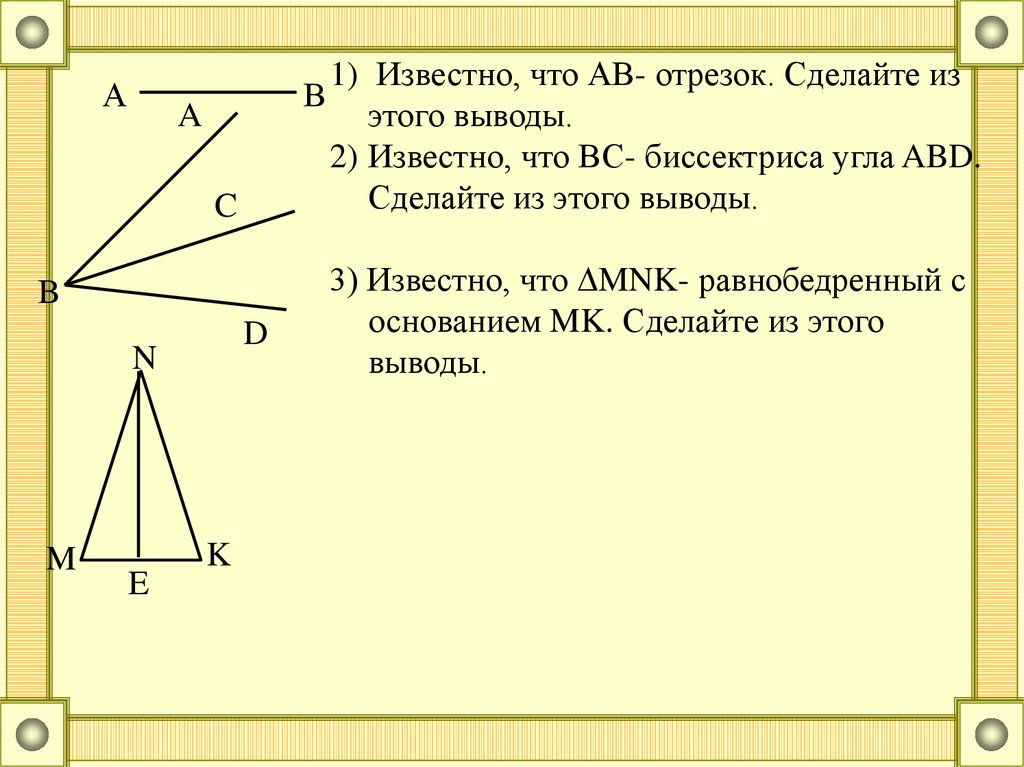
1) Известно, что АВ- отрезок. Сделайте из
этого выводы.
2) Известно, что ВС- биссектриса угла ABD.
Сделайте из этого выводы.
3) Известно, что MNK- равнобедренный с
основанием MK. Сделайте из этого
выводы.

6.

Методы доказательства
1.Синтетический метод
2. Восходящий анализ
3.Нисходящий анализ
4. Метод от противного
5. Метод исключения

7.

Синтетический метод
Доказательство математического предложения x M:
A(x) B(x) называется синтетическим, если оно осуществляется по
следующей логической схеме:
(A(x)∧T B1(x) B2(x) … Bn (x) B(x), где Т- определенная
совокупность предложений той теории, в рамках которой доказывается
данное предложение и которой принадлежат B1(x), B2(x),…, Bn (x),
составляющих доказательство, а также суждения A(x) и B(x).

8.

Аналитический метод
При аналитическом доказательстве теоремы x M: A(x) B(x)
цепочка силлогизмов строится так, что мысль движется от
заключения теоремы к её условию. Различают два вида
аналитического метода: восходящий анализ ( анализ Паппа),
нисходящий анализ (анализ Евклида)
Восходящий анализ
Восходящий анализ осуществляется по следующей схеме:
B(x) B1(x) B2(x) … Bn (x) A(x)

9.

Нисходящий анализ
Нисходящий анализ осуществляется по следующей схеме:
B(x) B1(x) B2(x) … Bn (x)

10.

Синтетический метод
B
A(x) В 1 В 2 … В n B(x)
Дано: AB, CD- хорды, E-точка пересечения C 2 4
хорд.
E
Доказать: AE BE=CE DE
N
3
Доказательство
1
Утверждения
Обоснования
A
1= 2
По 1 следствию из теоремы
о вписанном угле
3= 4
По свойству вертикальных
углов
AED∽ CEB
По 1 признаку подобия
треугольников
По определению подобных
треугольников
AE DE
AE BE=CE DE
CE
BE
По свойству пропорции
M
D

11.

Силлогизм3
БП: Если два угла одного треугольника соответственно равны
двум углам другого треугольника, то эти треугольники
подобны.
МП: Два угла 1и 3 треугольника AED соответственно равны
двум углам 2 и 4 треугольника CEB.
В: AED∽ CEB.
Силлогизм4
БП: В подобных треугольниках сходственные стороны
пропорциональны.
МП: Стороны AE, DE и CE, BE- сходственные стороны
подобных треугольников AED и CEB.
AE DE
В: CE BE

12.

Силлогизм5
БП: Произведение крайних членов пропорции равно
произведению средних членов.
МП: AE и BE –крайние члены, а DE и CE- средние
члены одной и той же пропорции.
В:AE BE=CE DE

13.

Силлогизм1
БП: Вписанные углы, опирающиеся на одну и ту же дугу
окружности, равны.
МП: Вписанные углы 1и 2 опираются на одну и ту же дугу
BMD.
В: 1= 2.
Силлогизм2
БП: Вертикальные углы равны.
МП: Углы 3 и 4 – вертикальные.
В: 3= 4.

14.

Восходящий анализ
Восходящий анализ осуществляется по следующей схеме:
B(x) B1(x) B2(x) … Bn (x) A(x)
Д а н о : ABCD- ромб, AC
и BD – диагонали
Д о ка з ат ь : AC BD
B
A
O
D
C
1) Для того чтобы доказать, что AC BD, достаточно
доказать, что BO AC. ( B1(x))
2) Для того чтобы доказать, что BO AC, достаточно
доказать, что ВО- высота треугольника АВС. ( B2(x))
3) Для того чтобы доказать, что ВО является высотой
треугольника АВС, достаточно доказать, что
треугольник АВС равнобедренный и ВО в нем
является медианой. ( B3(x))
4) Для того чтобы доказать, что треугольника АВС
равнобедренный, достаточно доказать, что в нем
АВ=ВС. ( B4(x))
5) АВ=ВС по условию(ABCD- ромб) и ВО – медиана
треугольника АВС(так как АО=ОС по свойству
диагоналей параллелограмма). ( A(x))

15.

Нисходящий анализ
Нисходящий анализ осуществляется по следующей схеме:
B(x) B1(x) B2(x) … Bn (x)
Д а н о : ABCDчетырехугольник, AB=CD,
AD=BC
Д о ка з ат ь : ABCDпараллелограмм
B
A
C
D
1) Пусть ABCD-параллелограмм (В(х))
2) Тогда BC AD и AB DC
(B1(x))
3) Тогда ACB= CAD, BAC= ACD (B2(x))
4) Из ACB= CAD, BAC= ACD и АС- общая
сторона
треугольников ABC и ADC, следует: ABC= ADC
(B3(x))
5) Тогда AD=BC, AB=DC
(A(x))
Итак, имеем B(x) B1(x) B2(x) B3(x) A(x),
А(х) – истинно.
A(x) B3(x) B2(x) B1(x) B(x) т.е. все
рассуждения обратимые.