Цилиндр. Верхний и нижний круги

1.

ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛА: ПРЕПОДАВАТЕЛЬ МАТЕМАТИКИ
ШМЕЛЁВА АЛЬБИНА ВАЛИЕВНА
БУ ПО «МЕЖДУРЕЧЕНСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ»

2.

×

3.

Цилиндр – это тело, заключенное между двумя кругами
расположенными в параллельных плоскостях и цилиндрической
поверхностью.
Цилиндр – это тело, которое описывает
прямоугольник при вращении вокруг одной из его
сторон.
Верхний и нижний круги – это основания цилиндра.
Прямая проходящая через центры кругов – это
ось цилиндра.
Отрезок , который образует поверхность цилиндра,
– это образующая цилиндра.
Радиус основания - это радиус цилиндра.
Высота цилиндра - это перпендикуляр между основаниями
цилиндра.

4.

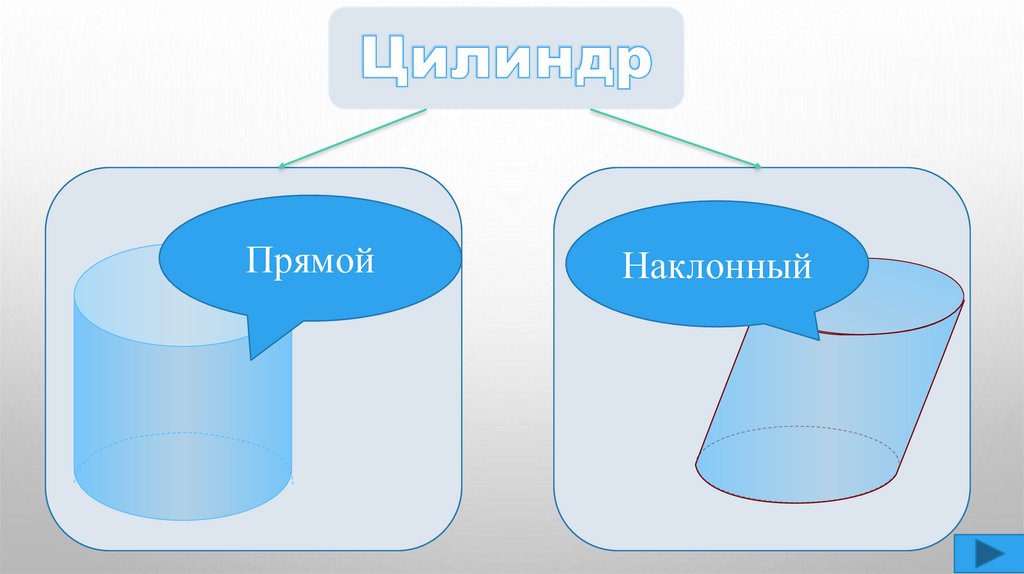
Прямой
Наклонный

5.

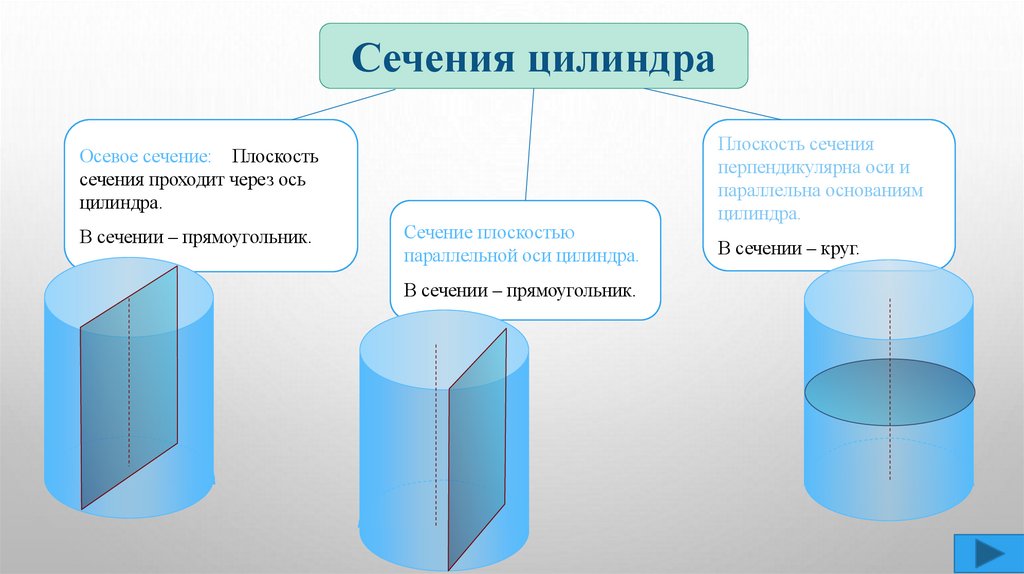
Сечения цилиндра
Осевое сечение: Плоскость
сечения проходит через ось
цилиндра.
В сечении – прямоугольник.
Сечение плоскостью
параллельной оси цилиндра.
В сечении – прямоугольник.
Плоскость сечения
перпендикулярна оси и
параллельна основаниям
цилиндра.
В сечении – круг.

6.

Когда стали строить здания из камня
пришлось перетаскивать каменные
глыбы. Для этого издавна применяли
катки. И было замечено, перекатка
тяжелого камня становилось легче,
если для катка взято прямое дерево и
от него отрезан кусок с почти
одинаковой толщиной в начале и
конце. Так люди познакомились с
одной из важнейших фигур –
цилиндром.
Скалками
цилиндрической
формы
пользовались и женщины, раскатывая
бельё после стирки.

7.

В жизни мы очень часто сталкиваемся с формой
цилиндра, поэтому возникает потребность в его
изучении .

8.

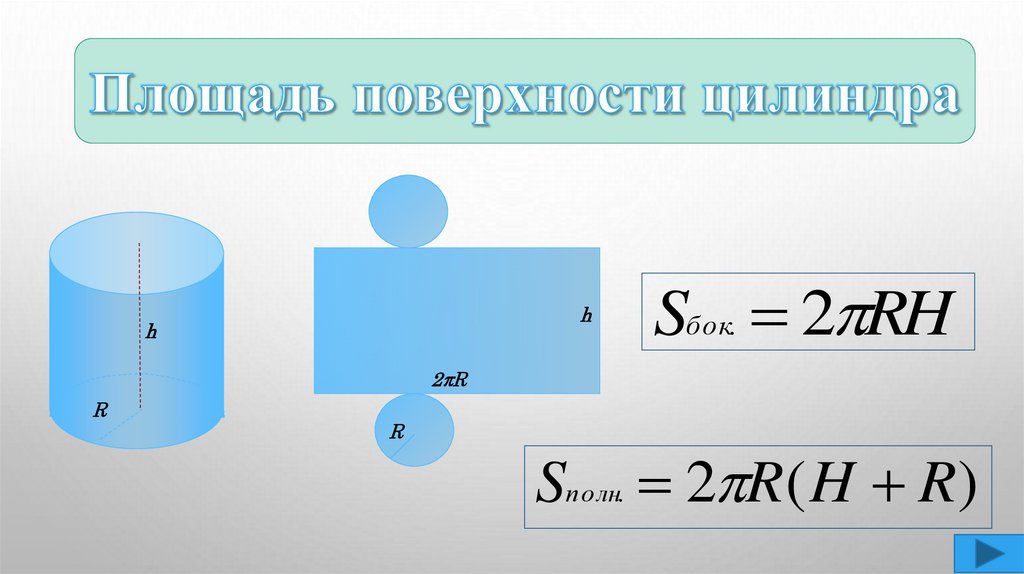
h
h
Sбок. 2 RH
2 R
R
R
Sпо лн. 2 R( H R)

9.

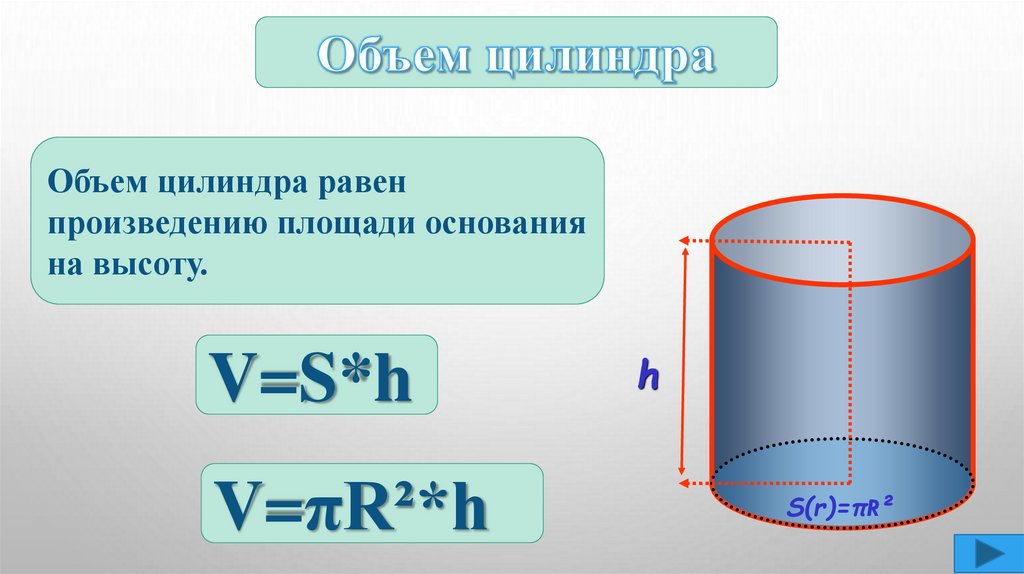
Объем цилиндра равен
произведению площади основания
на высоту.
V=S*h
V=πR²*h
h
S(r)=πR²

10.

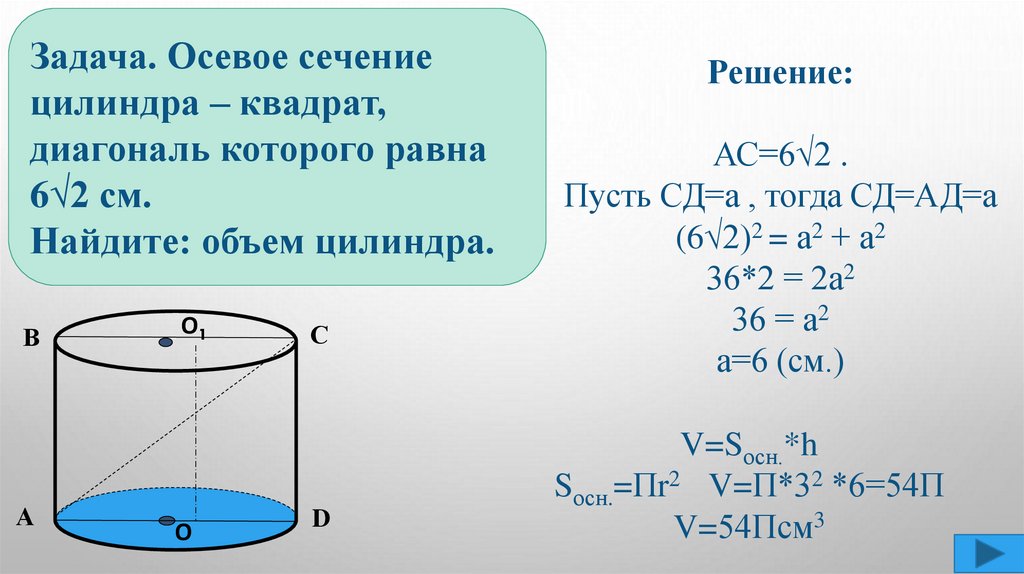
Задача. Осевое сечение
цилиндра – квадрат,
диагональ которого равна
6√2 см.
Найдите: объем цилиндра.
В
А
О1
О
С
D
Решение:
АС=6√2 .
Пусть СД=а , тогда СД=АД=а
(6√2)2 = а2 + а2
36*2 = 2а2
36 = а2
а=6 (см.)
V=Sосн.*h
Sосн.=Пr2 V=П*32 *6=54П
V=54Псм3

11.

Каждая группа студентов работает с моделью
цилиндра, представленной на его столе.
Задание: Вычислить по модели, используя
измерительные приборы:
• Площадь полной поверхности
• Площадь боковой поверхности
• Площадь основания
• Радиус
• Высоту