Похожие презентации:
Цилиндр. Решение задач
1.
«Цилиндр.Решение задач »
2. Примеры цилиндров
Слово цилиндр означает отгреческого слова
“валик”, “каток”.
3.
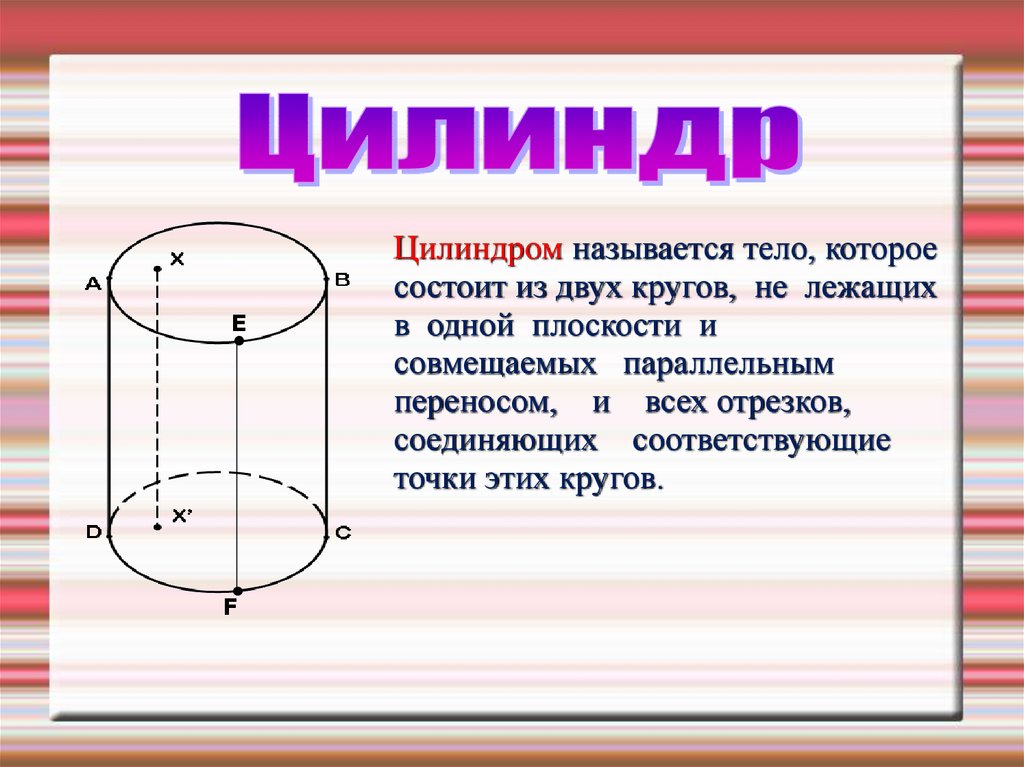
EF
Цилиндром называется тело, которое
состоит из двух кругов, не лежащих
в одной плоскости и
совмещаемых параллельным
переносом, и всех отрезков,
соединяющих соответствующие
точки этих кругов.
4.
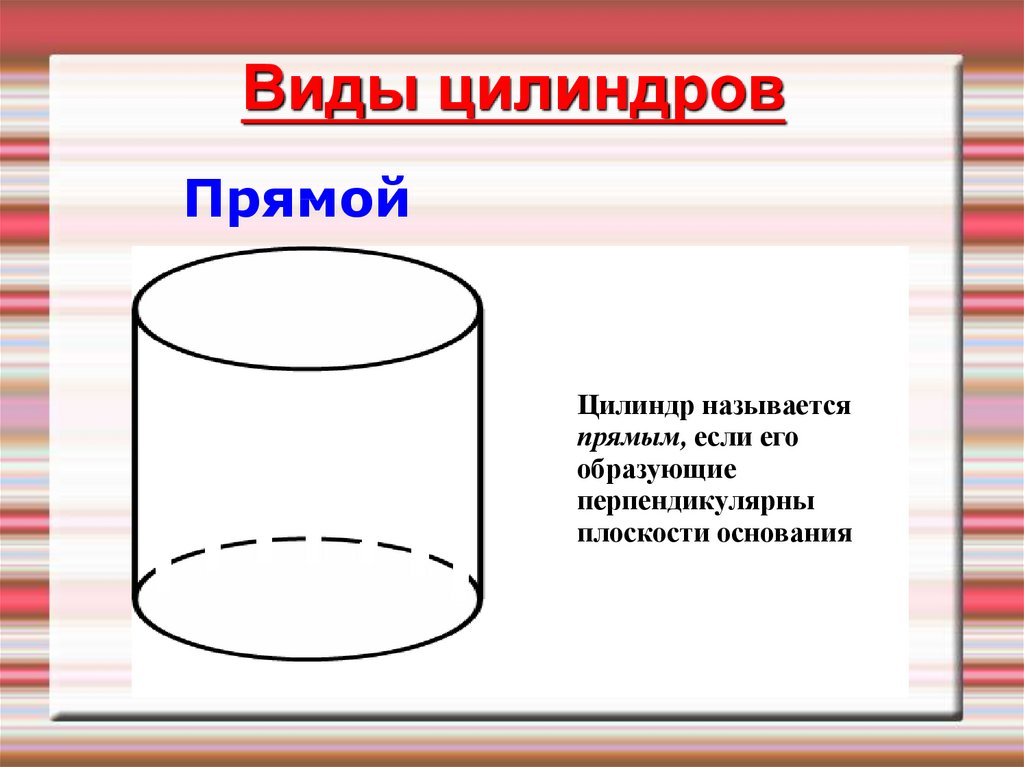
Виды цилиндровПрямой
Цилиндр называется
прямым, если его
образующие
перпендикулярны
плоскости основания
5.
Виды цилиндровНаклонный
Цилиндр называется
наклонным, если его
образующие
наклонены к
основанию под
некоторым углом
6.
Круги, лежащие впараллельных плоскостях,
называются основаниями
цилиндра, а отрезки,
соединяющие
соответствующие точки
окружностей оснований –
называются образующими
цилиндра.
Получить цилиндр
можно:
Вращением
прямоугольника
вокруг одной из
его сторон
7.
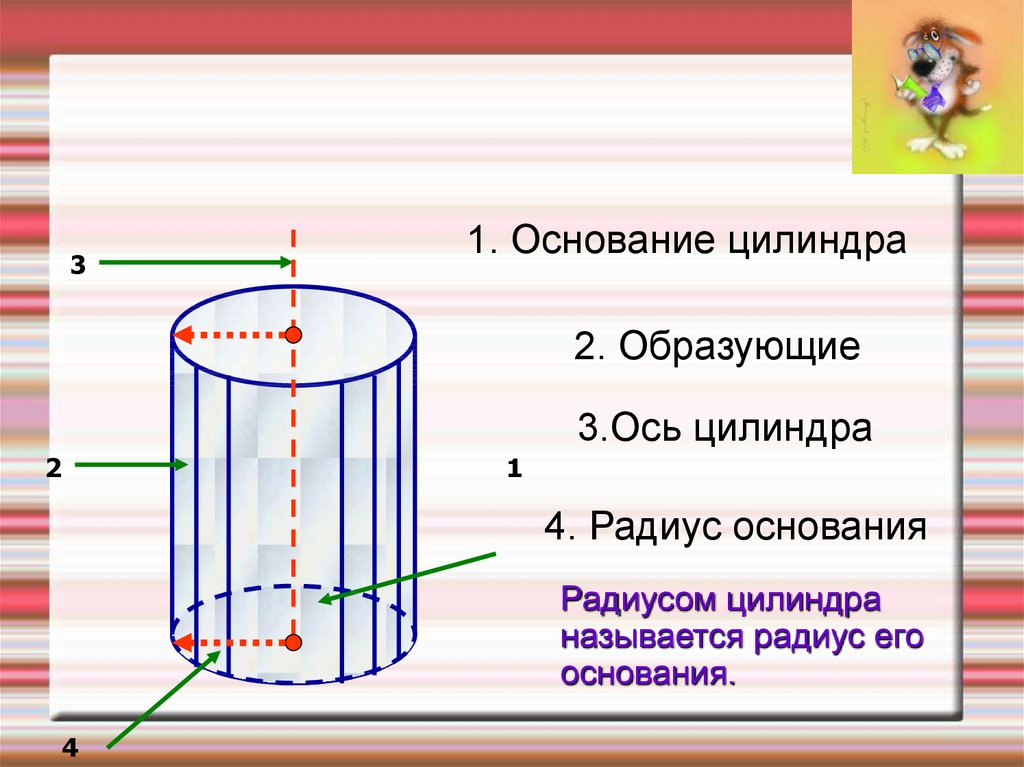
1. Основание цилиндра3
4
2. Образующие
3.Ось цилиндра
2
1
4. Радиус основания
Радиусом цилиндра
называется радиус его
основания.
4
8.
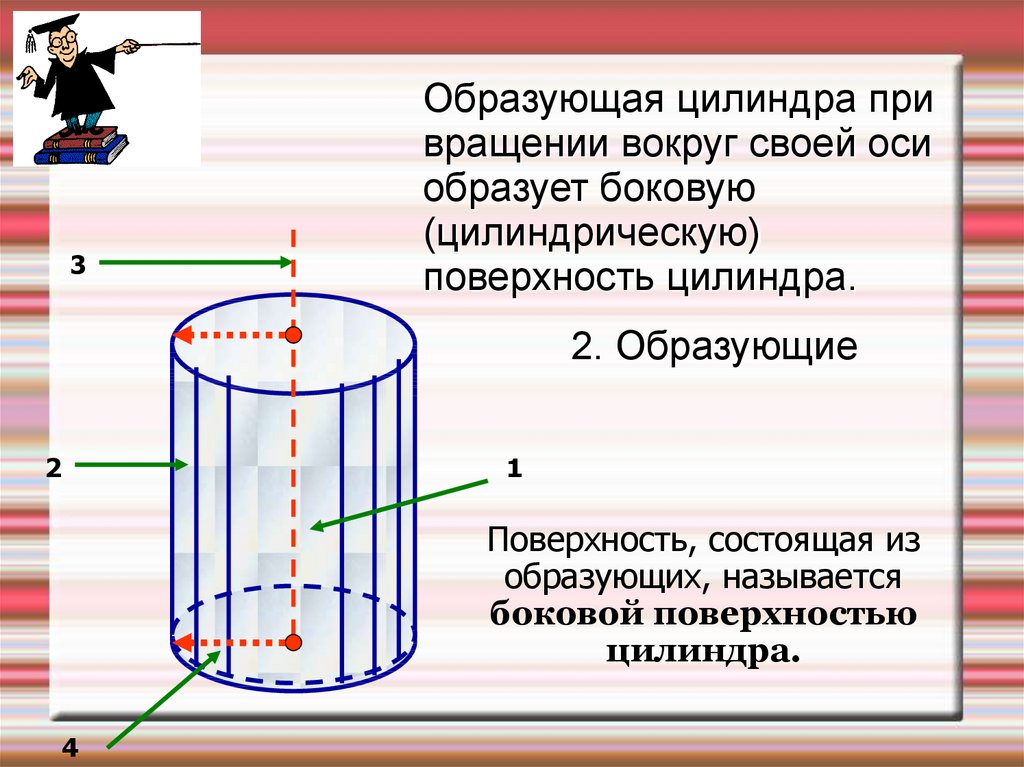
Образующая цилиндра привращении вокруг своей оси
образует боковую
(цилиндрическую)
поверхность цилиндра.
3
4
2
2. Образующие
1
Поверхность, состоящая из
образующих, называется
боковой поверхностью
цилиндра.
4
9. Понятие цилиндрической поверхности, цилиндра
10.
Сечения цилиндраСечение , параллельное оси
цилиндра-прямоугольник
о1
α
γ
β
β
о
Сечение плоскостью,
перпендикулярной к оси или
параллельное основаниям,
является кругом.
11. Сечения цилиндра
Осевое сечение - прямоугольникО
О
12. Сечения, параллельные оси цилиндра - прямоугольники
13.
Разверткой боковой поверхностицилиндра является прямоугольник
со сторонами Н и С, где Н – высота
цилиндра, а С – длина окружности
основания.
S=πR²
н
С=2πR
S=πR²
14.
4.Плошадь поверхности цилиндраS=πR²
Sосн=πR²
н
С=2πR
S=πR²
S(бок.поверхн.)= 2πRh
S(полн.поверхн.)=2πR²+2πRh
S(полн.поверхн.)=2πR(R+h)
15. Задача №1:Найти площадь полной поверхности цилиндра
Решение задачЗадача №1:Найти площадь полной
поверхности цилиндра
В
5
А
45º
r
С
АВС
- прямоугольный
АВС
- равнобедренный
ВС=АС=5
r=2,5
S=2πr(h+r)
S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5π
16.
Задача №2:Площадь осевого сеченияцилиндра равна 10 м2, а площадь основания
равна 5 м2. Найдите высоту цилиндра.
R 5,
2 R H 10
2
В
O1
С
H
А
R
O
5
R=
H
D
H=
5
2
5
5
H
м












 Математика
Математика








