Похожие презентации:
Комплексные числа
1. Комплексные числа
2.
Комплексным числом называетсячисло вида
z x y i,
где x и y – вещественные числа.
3.
z x yiназывается алгебраической формой
записи комплексного числа.
4.
Число x называется действительной частью,y–мнимой частью комплексного числа z.
Это записывают следующим образом:
x Rez,
y Im z.
5.
• Если x 0 , то числочисто мнимым.
z называют
• Если y 0 , то получается z x 0 i
вещественное число.
• Два комплексных числа z x yi
и z x yi
называются
сопряженными.
6.
Два комплексных числа z1 x1 y1iz2 x2 y2i
равны друг другу, если x1 x2 и y1 y2 ;
комплексное число z считается
равным нулю, если x=y=0.
и
7.
Всякое комплексное число можноизобразить точкой на плоскости, т.к.
каждому z соответствует
упорядоченная пара вещественных
чисел (x;y).
8. Модуль комплексного числа
Число x 2 y 2 называется модулемкомплексного числа z x yi и
обозначается z .
9. Тригонометрическая форма комплексного числа.
z r sin i sinr x y
2
2
y
arctg
x
10. Показательная форма комплексного числа
z r ei
r x y
2
2
y
arctg
x
11. Действия над комплексными числами
z1 z 2 x1 x2 y1 y2 iz1 z2 x1 x2 y1 y2 i
12. Действия над комплексными числами
z1 z 2 x1 iy1 x2 iy 2x1 x2 iy1 x2 ix1 y2 i y1 y2
2
x1 x2 y1 y2 x1 y2 x2 y1 i
13.
z z x yi x yix yi x y
2
2 2
2
2
14. Действия над комплексными числами
z1 x1 y1i x1 y1i x2 y2iz2 x2 y2i x2 y2i x2 y2i
15.
x1 x2 y1 x2i x1 y2i y1 y2i2
2
x2 y2
2
x x y y x y x y i
1 2
1
2
x y
2
2
2
2
2
1
1
2
16. Действия над комплексными числами
i 1z1 z2 r1 e r2 e
i 2
r1r2 e
i ( 1 2 )
z1 r1 e
r1 i
e
i
z 2 r2 e
r2
i 1
1
2
2
17.
z1 z 2 r1 cos 1 i sin 1 r2 cos 2 i sin 2r1r2 cos 1 2 i sin 1 2
z1 r1 cos 1 i sin 1
z 2 r2 cos 2 i sin 2
r1
cos 1 2 i sin 1 2
r2
18. Формулы Муавра
z r cos n i sin nn
n
19.
n2kπ
2kπ
z r cos
i sin
n
n
n
k 0, 1, 2,...,n 1












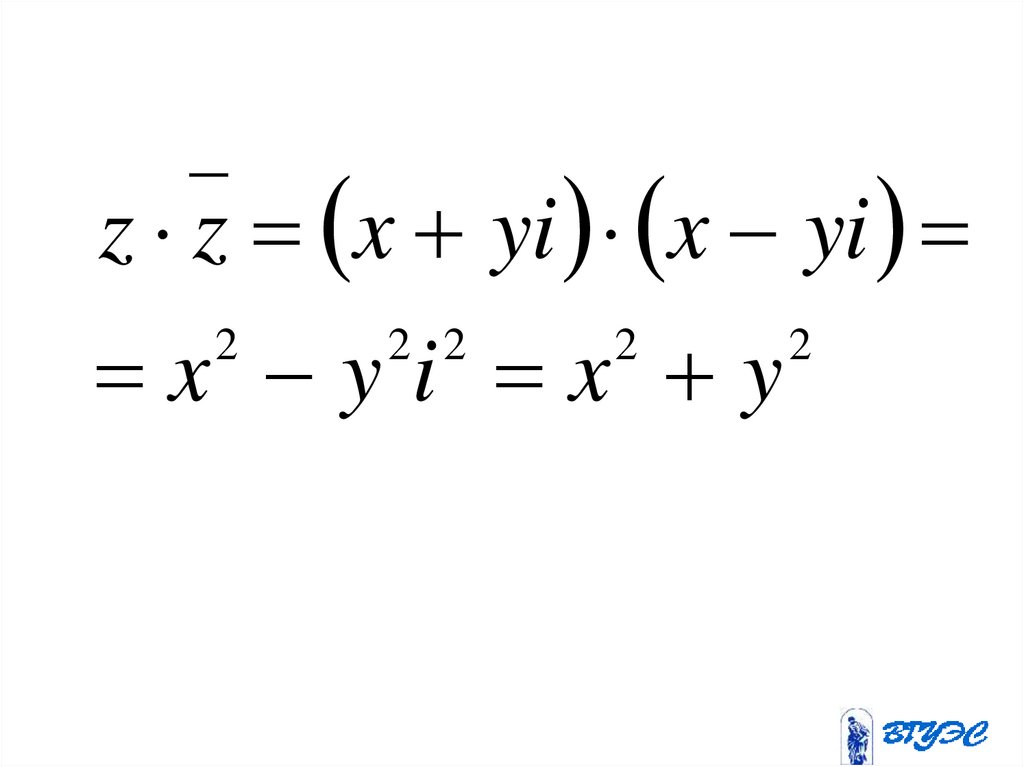

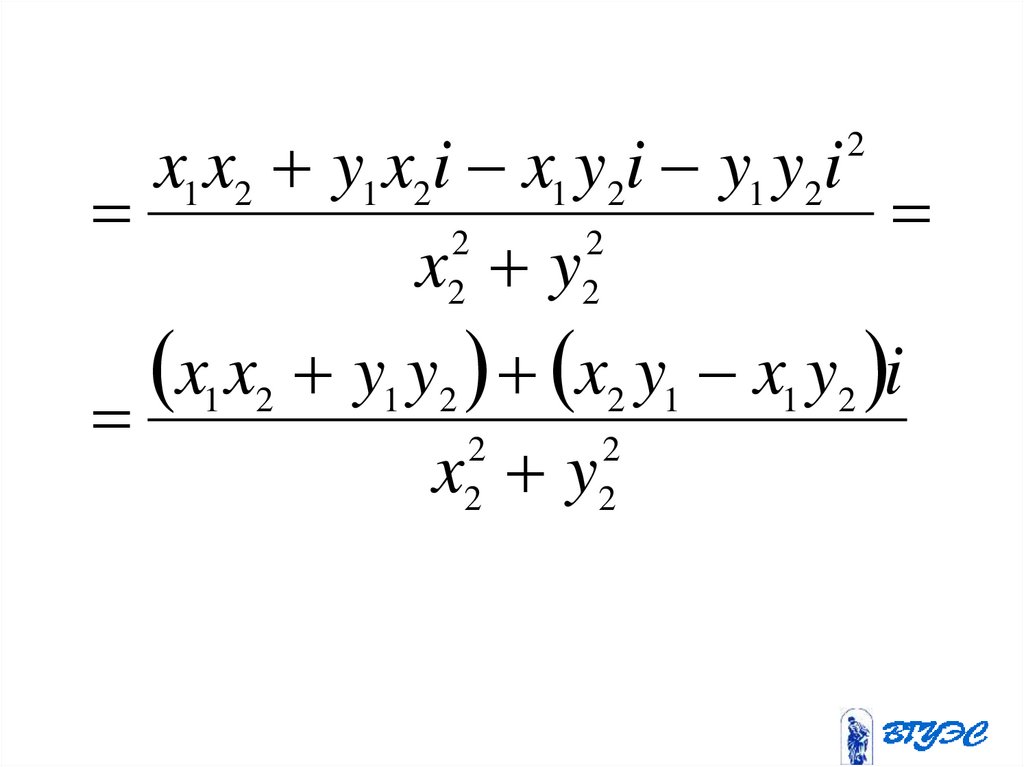

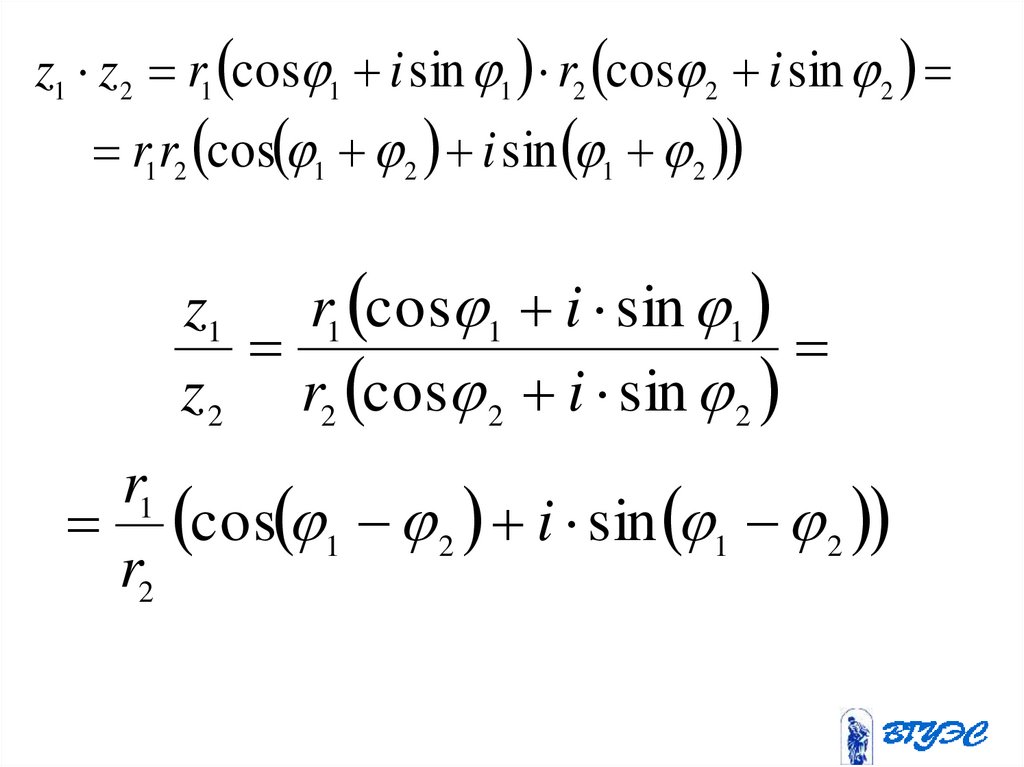

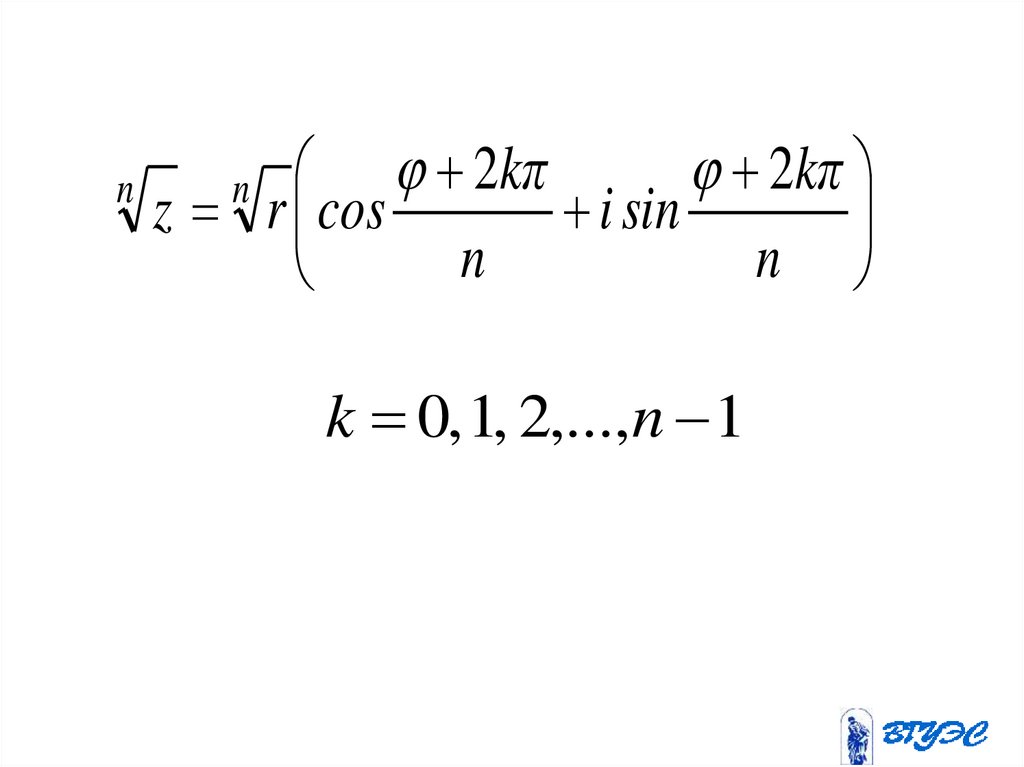
 Математика
Математика








