Похожие презентации:
Использование многофакторных моделей на основе главных компонент для прогнозирования состояния социально-экономических систем
1. Тема 5. ИСПОЛЬЗОВАНИЕ МНОГОФАКТОРНЫХ МОДЕЛЕЙ НА ОСНОВЕ ГЛАВНЫХ КОМПОНЕНТ ДЛЯ ПРОГНОЗИРОВАНИЯ СОСТОЯНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
Тема 5. ИСПОЛЬЗОВАНИЕМНОГОФАКТОРНЫХ
МОДЕЛЕЙ НА ОСНОВЕ
ГЛАВНЫХ КОМПОНЕНТ
ДЛЯ ПРОГНОЗИРОВАНИЯ
СОСТОЯНИЯ СОЦИАЛЬНОЭКОНОМИЧЕСКИХ
СИСТЕМ
1
1
2.
ПРОГНОЗИРОВАНИЕ НА ОСНОВЕГЛАВНЫХ КОМПОНЕНТ
Пространство состояний социально-экономической системы
будет описываться в виде
X
0
0
[ x1
0
x2
0
xn ]
(1)
Показатели социально-экономической системы, определяемые
по такой модели, вычисляются по формуле
et
xki
2
p
xi v hi z kh
(2)
h 1
2
3.
ПРОГНОЗИРОВАНИЕ НА ОСНОВЕГЛАВНЫХ КОМПОНЕНТ
Сценарное прогнозирование заключается в задание сценария в
виде изменения показателей социально-экономической системы
и вычисление по этим сценарным показателям значений главных
компонент.
Для вычисления используется система уравнений вида
3
p
sc
x k1 x1 v hi z kh
h 1
x sc x p v z
2
hi kh
k2
h 1
p
sc
x kp x p v hi z kh
h 1
(3)
3
4.
ПРОГНОЗИРОВАНИЕ НА ОСНОВЕРЕГРЕССИОННЫХ МОДЕЛЕЙ
Построение регрессионной модели начинается с выдвижения
гипотезы о том, что переменная зависит от набора эндогенных
(независимых) переменных
y 1 x1 2 x 2 n x n
(1а)
или
y X
4
(1б)
4
5.
РЕГРЕССИОННАЯ МОДЕЛЬНа практике вместо генеральной совокупности используется
выборка данных,
y X
(2)
- оценка коэффициентов регрессии
Минимизируется функционал (метод наименьших квадратов)
(X y) ( X y)
T
(3)
В результате получаем
X
5
T
T
X X y 0
(4)
5
6.
РЕГРЕССИОННАЯ МОДЕЛЬС учетом формулы
1 XT X
A m
уравнение (4) преобразуется к виду
mA X y
T
(5)
Решая полученное уравнение, получается
1m A 1 X T y
6
(6)
6
7.
РЕГРЕССИОННАЯ МОДЕЛЬМатрица
A
может быть представлена
T
A V0 V0
(7)
Подставляя соотношение (7) в уравнение (5) получим
T
T
mV0 V0 X
7
y
(8)
7
8.
РЕГРЕССИОННАЯ МОДЕЛЬДалее умножаем справа на матрицу
T
T
T T
mV0 V0 V0 V0 X
y
(9)
После небольших преобразований получается соотношение
1 T T
1
m V0 V0 X y
1
8
n
1
T T
v 0i v 0 i X
i
m i 1
(10)
y
8
9.
РЕГРЕССИОННАЯ МОДЕЛЬОдним из путей повышения качества регрессионной модели
является удаление членов, соответствующих очень маленьким ,
которое приводит вычислению оценки
1
9
p
1
T T
v 0i v 0i X
i
m i 1
y
(11)
9
10.
РЕГРЕССИЯ ГЛАВНЫХ КОМПОНЕНТРегрессионное уравнение, использующее в качестве
независимых переменных главные факторы, имеет вид
y Z
(12)
Для получения оценки вектора также используется метод
наименьших квадратов, в результате чего получаем уравнение
Z
10
T
Z Z y 0
T
(13)
10
11.
РЕГРЕССИЯ ГЛАВНЫХ КОМПОНЕНТГлавные факторы и исходные факторы связаны соотношением
T
Z = V0 X
(14)
С учетом соотношения (14) уравнение (13) преобразуется к
виду
V0 X
T
T
T
XV0 (XV0 )
y
(15)
или
11
T
T
mV0 AV0 (XV0 )
y
11
12.
РЕГРЕССИЯ ГЛАВНЫХ КОМПОНЕНТВ соответствии с соотношением (7) уравнение (15) преобразуется
T
T
T
mV0 V0 ΣV0 V0 (XV0 )
y
С учетом ортогональности собственных векторов
(16)
T
V0 V0
I
Уравнение (16) преобразуется
mΣ ( XV0 ) y
T
12
(17)
12
13.
РЕГРЕССИЯ ГЛАВНЫХ КОМПОНЕНТВ итоге получаем оценку вектора
1
T
T
1
m V0 X y
(18)
Для уменьшения колебаний оценки коэффициентов вводится
смещение в оценку коэффициентов
13
p
1
T T
1
v 0i v 0i X
i
m i m 1
y
(10)
13
14.
Выбор числа главных компонентОбщая изменчивость процесса изменения
признаков определяется как
n
i
i
Наиболее простая стратегия выбора числа главных компонент
представляет простое удаление главных компонент, вариации
которых меньше некоторого граничного значения
i c
Критерий Кайзера. В соответствие с этим критерием
отбираются только факторы, с собственными значениями,
большими дисперсий отдельных факторов.
14
14
15.
Выбор числа главных компонентКритерий каменистой осыпи.
Критерий «каменистой осыпи» базируется на графическом
представлении собственных значений.
15
15
16.
Оценка качества регрессионноймодели
Сумма квадратов, объясняемая регрессией (СКР) – это сумма
возведённых в квадрат разностей между прогнозируемыми
величинами зависимой переменной и средней величиной
наблюдаемых значений зависимой переменной
CKP ( yˆ y)
2
Общая сумма квадратов отклонений (ОСК) – это сумма
возведённых в квадрат разностей между наблюдаемой
величиной зависимой переменной и средней наблюдаемых
величин зависимо переменной
16
ОСК ( yi y )
2
16
17.
Оценка качества регрессионноймодели
Результат деления СКР на ОСК называется коэффициентом
детерминации
СКР
R
ОСК
2
Например, если коэффициент детерминации равен 0.4, то
регрессионная модель может объяснить 40% дисперсии
критериального показателя, остальные же 60% определяются
факторами, которые отсутствуют в модели.
17
17
18.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
Точки из генеральной совокупности попадают в выборку
случайным образом, по этому в соответствии с теорией
вероятности среди прочих случаев возможен вариант, когда
выборка из “широкой” генеральной совокупности окажется
“узкой”
18
18
19.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
В случае «узкой» выборки:
а) уравнение регрессии, построенное по выборке, может
значительно отличаться от уравнения регрессии для генеральной
совокупности, что приведет к ошибкам прогноза;
б) коэффициент детерминации и другие характеристики
точности окажутся неоправданно высокими и будут вводить в
заблуждение о прогнозных качествах уравнения.
19
19
20.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
Один из наиболее часто используемых вариантов проверки
заключается в следующем. Для полученного уравнения
регрессии определяется F -статистика – характеристика точности
уравнения регрессии, представляющая собой отношение той
части дисперсии зависимой переменной которая объяснена
уравнением регрессии к необъясненной (остаточной) части
дисперсии.
20
20
21.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
Для осуществления статистической проверки значимости
уравнения регрессии формулируется нулевая гипотеза об
отсутствии связи между переменными (все коэффициенты при
переменных равны нулю) и выбирается уровень значимости
Уровень значимости – это допустимая вероятность совершить
ошибку первого рода – отвергнуть в результате проверки верную
нулевую гипотезу.
Чем выше уровень значимости (чем меньше ), тем выше
уровень надежности теста, равный1 , т.е. тем больше шанс
избежать ошибки признания по выборке наличия связи у
генеральной совокупности на самом деле несвязанных между
собой переменных.
21
21
22.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
Для выбранного уровня значимости по распределению Фишера
определяется табличное значение
.
сравнивается с фактическим значением критерия для
регрессионного уравнения .
Если выполняется условие
то ошибочное обнаружение связи будет происходить с
вероятностью меньшей чем уровень значимости.
В соответствии с правилом “очень редких событий не бывает”,
приходим к выводу, что установленная по выборке связь между
переменными имеется и в генеральной совокупности.
22
22
23.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
Если же оказывается
то уравнение регрессии статистически не значимо.
Иными словами существует реальная вероятность того, что по
выборке установлена не существующая в реальности связь
между переменными.
23
23
24.
ПРОВЕРКА ЗНАЧИМОСТИУРАВНЕНИЯ РЕГРЕССИИ
После того как выполнена проверка статистической значимости
регрессионного уравнения в целом полезно, особенно для
многомерных зависимостей осуществить проверку на
статистическую значимость полученных коэффициентов
регрессии.
Полученные фактические значения критерия Стьюдента
сравниваются с табличными значениями , полученными из
распределения Стьюдента. Если оказывается, что
то соответствующий коэффициент статистически значим, в
противном случае нет.
24
24
25.
Критические точки распределенияСтьюдента
1
2
3
4
40
60
120
25
0.10
Уровень значимости
(двусторонняя критическая область)
0.05
0.02
0.01
0.002
0.001
6.31
2.92
2.35
2.13
1.68
1.67
1.66
1.64
12.7
4.30
3.18
2.78
2.02
2.00
1.98
1.96
637.0
31.6
12.9
8.61
3.55
3.46
3.37
3.29
31.82
6.97
4.54
3.75
2.42
2.39
2.36
2.33
63.7
9.92
5.84
4.60
2.70
2.66
2.62
2.58
318.3
22.33
10.22
7.17
3.31
3.23
3.17
3.09
25
26.
Оценка ошибок прогнозаОшибки прогноза
ei yi yˆi
Среднее абсолютное отклонение (Mean Absolute Derivation,
MAD) измеряет точность прогноза, усредняя величины
ошибок прогноза
e MAD
26
1 m
y i yˆ i
m i 1
26
27.
Оценка ошибок прогнозаСреднеквадратическая ошибка (Mean Squared Error, MSE)
e MSE
1 m
2
( y i yˆ i )
m i 1
Средняя абсолютная ошибка в процентах (Mean Absolute
Percentage Error, МАРЕ)
1 n yi yˆ i
MAPE
n i 1 yi
27
27
28.
Оценка ошибок прогнозаСтандартная ошибка оценки
m
( yi yˆ i ) 2
eSSE
i 1
m n 1
Относительная среднеквадратическая ошибка
m
2
(
y
y
)
i ˆi
eMSEN
i 1
m
2
y
i
28
i 1
28
29.
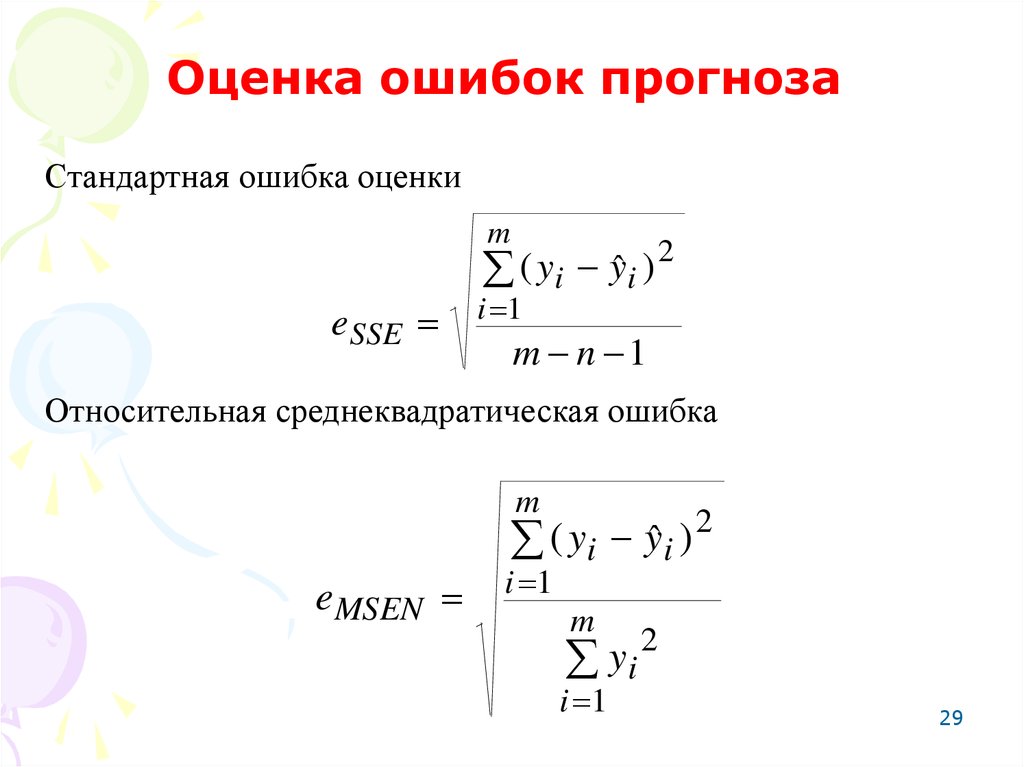
Оценка ошибок прогнозаСтандартная ошибка оценки
m
( yi yˆ i ) 2
eSSE
i 1
m n 1
Относительная среднеквадратическая ошибка
m
2
(
y
y
)
i ˆi
eMSEN
i 1
m
2
y
i
29
i 1
29




























 Математика
Математика








