Похожие презентации:
Плоскости. Лекция 2
1. Плоскости
2.
Способы задания плоскости начертеже
А2
m2
С2
М2
K2
f2
n2
e2
В2
e1
n1
В1
K1
f1
m1
А1
С1
М1
2
3. Расположение плоскостей относительно плоскостей проекций
ПЛОСКОСТИОбщего
положения
Частного
положения
Проецирующие
плоскости
На одной из плоскостей
проекций изображен
угол наклона в
натуральную
величину
Плоскости
уровня
На одной из плоскостей
проекций плоскость
изображена в натуральную
величину
3
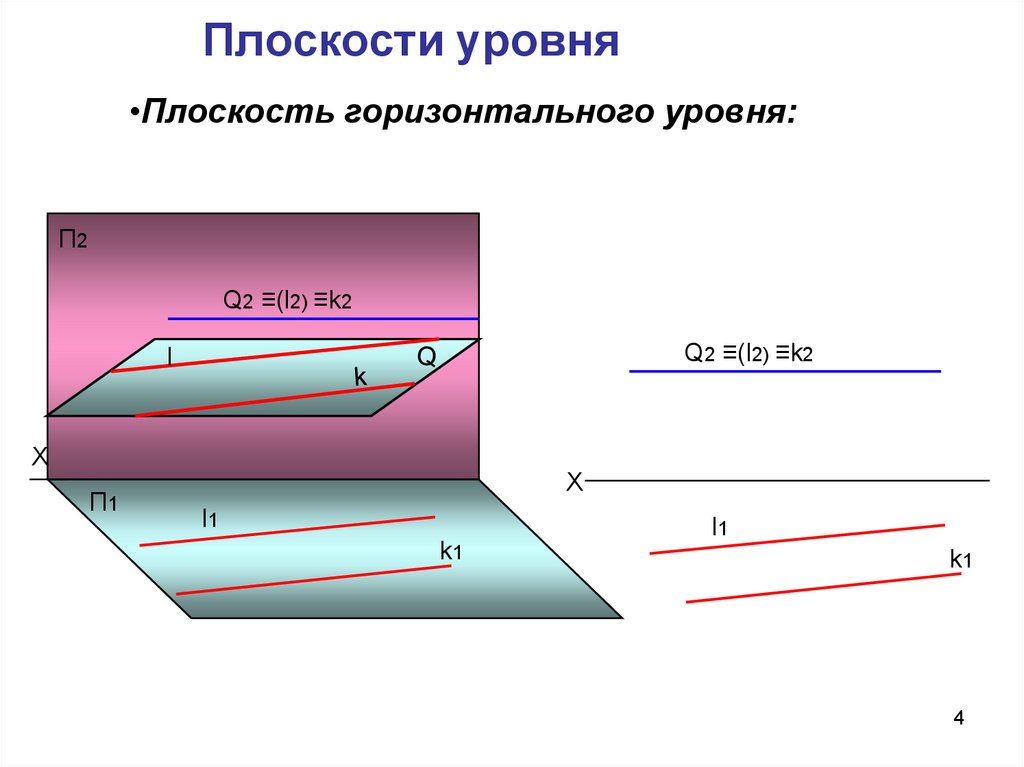
4. Плоскости уровня
•Плоскость горизонтального уровня:П2
Q2 ≡(l2) ≡k2
Q2 ≡(l2) ≡k2
l
Х
П1
Х
l1
l1
k1
k1
4
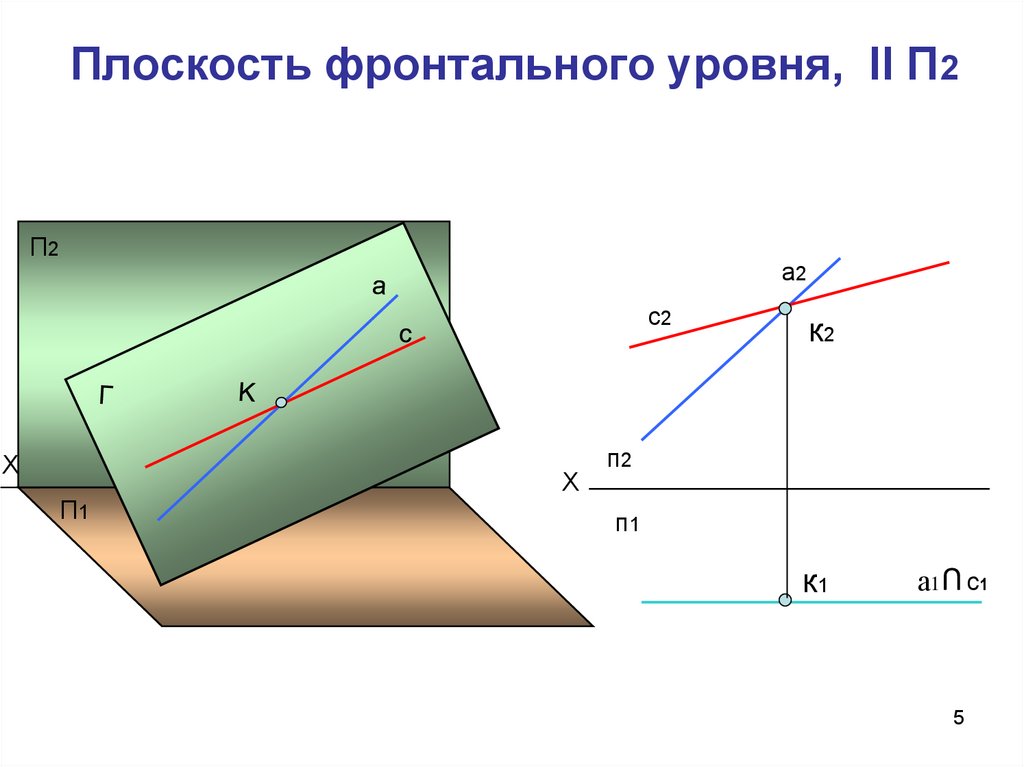
5. Плоскость фронтального уровня, ll П2
П2а2
с2
П1
Х
п2
п1
к1
U
Х
к2
а1 с1
5
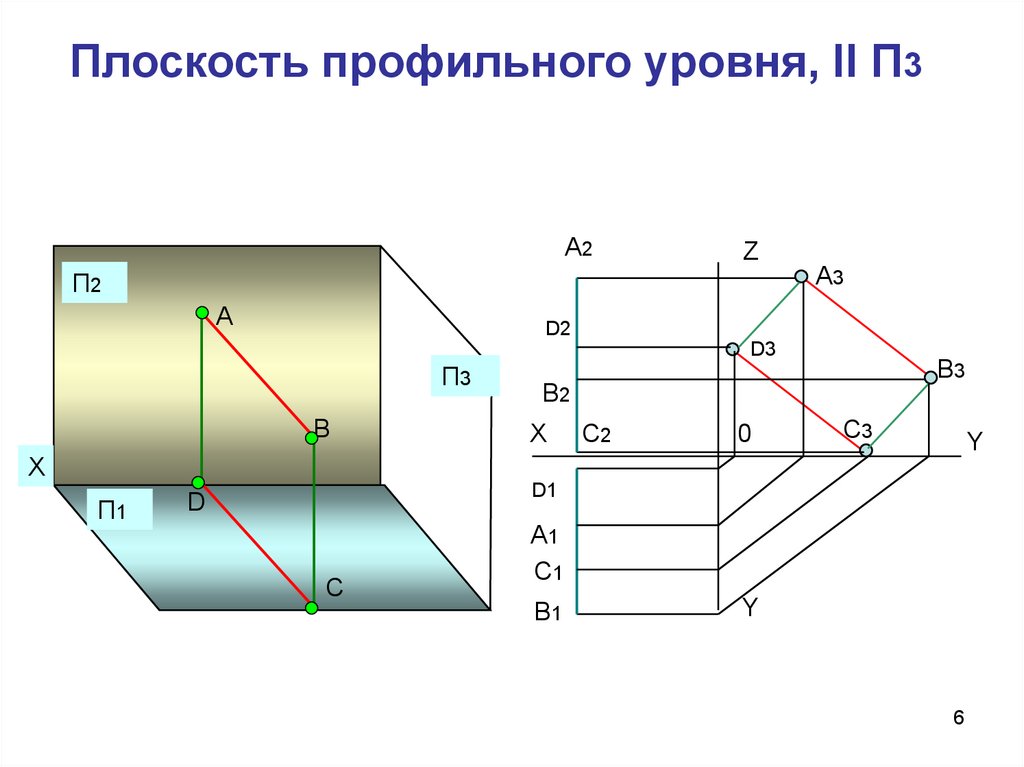
6.
Плоскость профильного уровня, ll П3А2
Z
П2
А
А3
D2
D3
П3
В
В3
В2
Х
С2
0
С3
Y
Х
П1
D1
D
С
А1
С1
В1
Y
6
7. Частное положение плоскости в пространстве
Горизонтально-проецирующее, П1;П2
N2
G
N
m
m2
K2
K
Х
Х
β
П1
(K1) N1
K1
m1
m1
7
8. Фронтально-проецирующая плоскость, П2
Фронтально-проецирующая плоскость, П2П2
Q2 ≡b2
Q2 ≡b2
Q
α
Х
M2 ≡ с2
П1
b
с
Х
M2 ≡ с2
c1
α
M≡M1
b1
M1
8
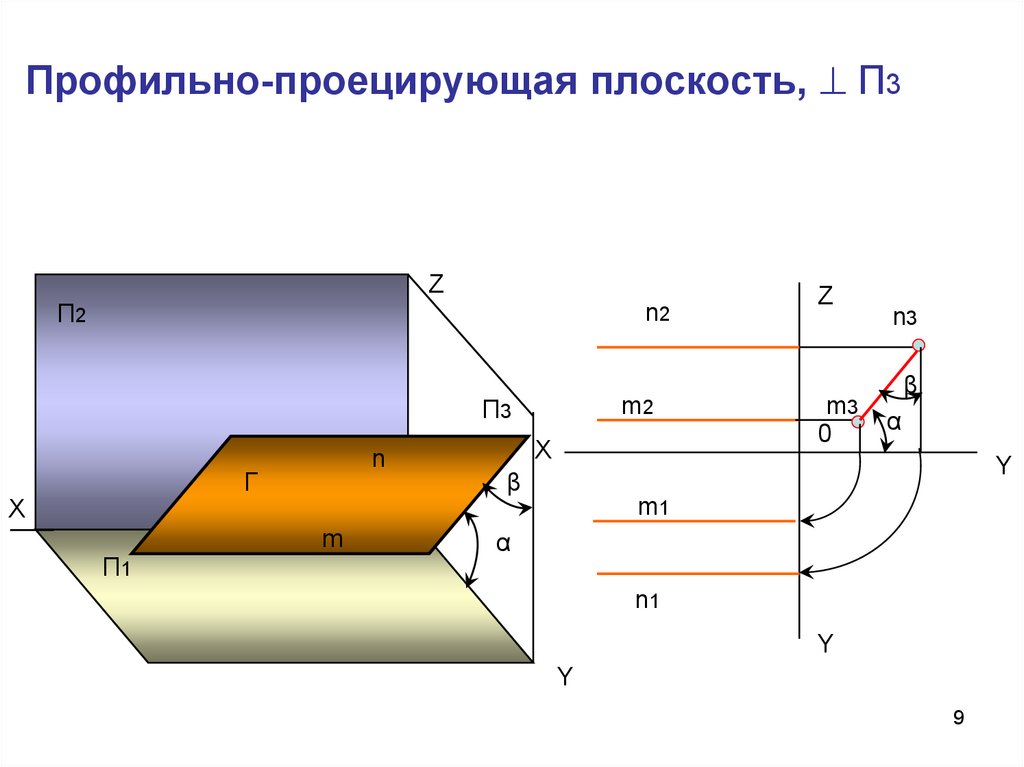
9. Профильно-проецирующая плоскость, П3
Профильно-проецирующая плоскость, П3Z
П2
n2
П3
n
Г
Х
m2
Х
Z
m3
0
n3
β
α
Y
β
m1
П1
m
α
n1
Y
Y
9
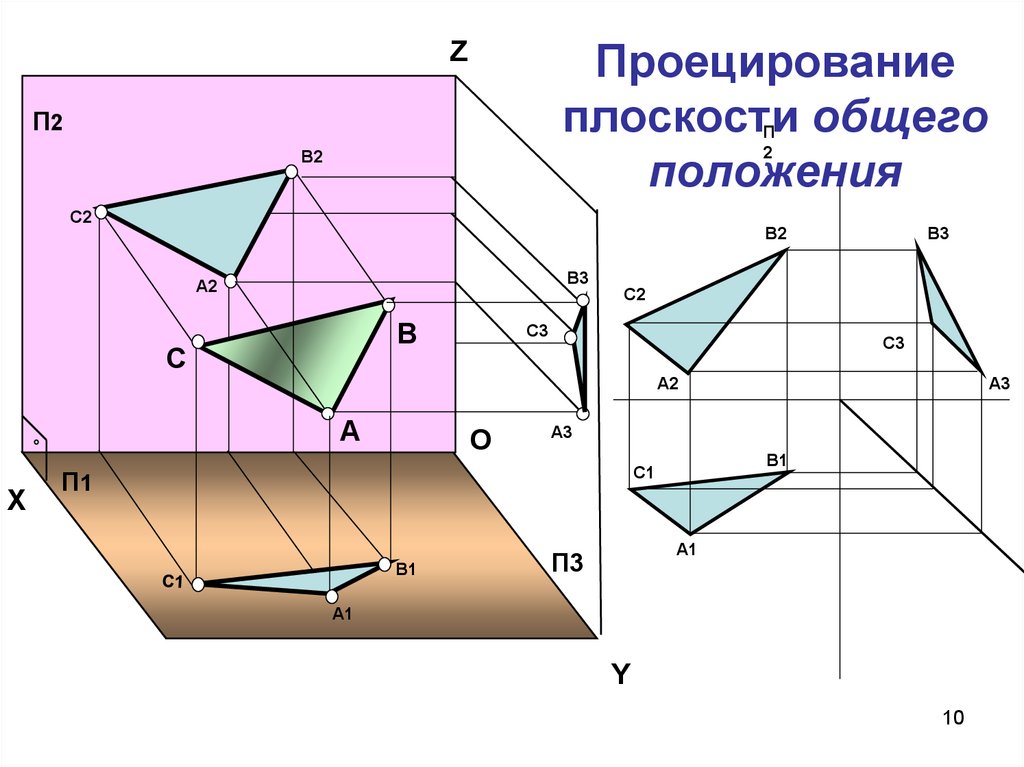
10. Проецирование плоскости общего положения
ZП2
П
2
В2
С2
В2
В3
А2
В
С
С2
С3
С3
А2
А
X
В3
0
П1
В1
О
А3
А3
В1
С1
А1
П3
А1
Y
10
11. Принадлежность точки и линии плоскости
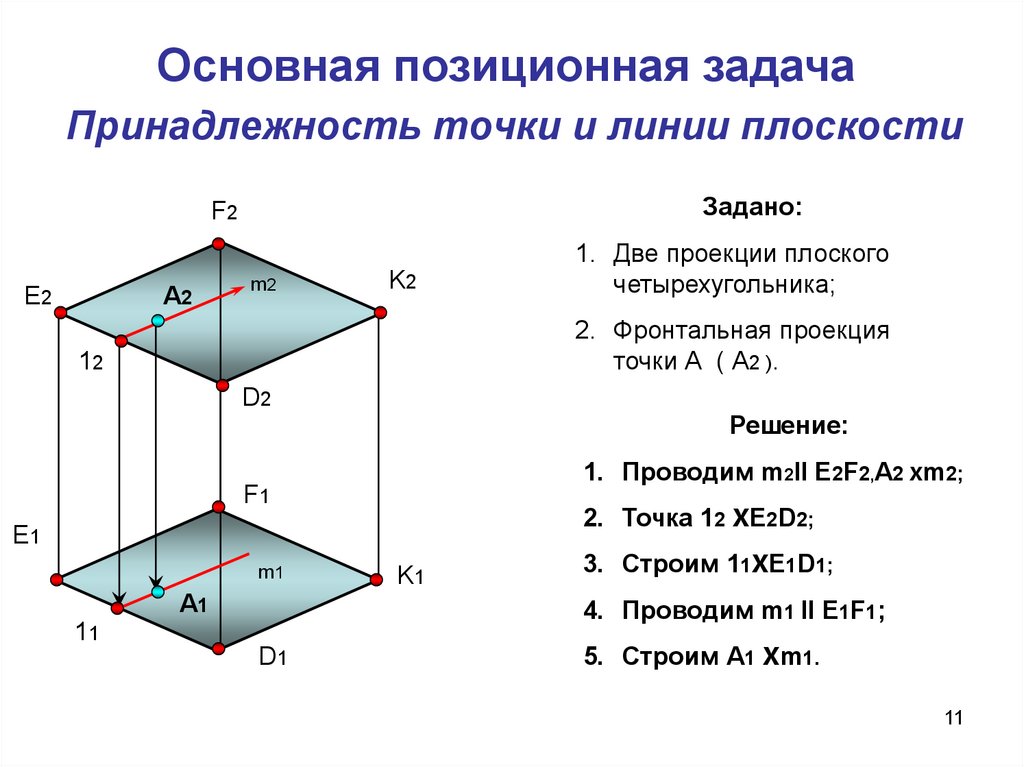
Основная позиционная задачаПринадлежность точки и линии плоскости
Задано:
F2
Е2
А2
m2
K2
1. Две проекции плоского
четырехугольника;
2. Фронтальная проекция
точки А ( А2 ).
12
D2
Решение:
1. Проводим m2ll E2F2,A2 Xm2;
F1
2. Точка 12 XE2D2;
Е1
m1
А1
K1
3. Строим 11XE1D1;
4. Проводим m1 ll E1F1;
11
D1
5. Строим А1 Xm1.
11
12. Линии частного положения в плоскости (главные линии плоскости)
К2f2
D2
22 h2
12
а2
М2
а2
b2
b2
b1
X
h1
М1
а1
а1
f1
21
11
b1
D1
К1
h - горизонталь
f - фронталь
12
13. Взаимное расположение плоскостей
1. Параллельность плоскостей: если плоскости параллельны, тодве пересекающиеся прямые одной плоскости параллельны двум
пересекающимся прямым другой плоскости
2. Пересечение плоскостей: результатом пересечения двух
плоскостей является прямая линия, для построения которой
достаточно найти две точки общие для пересекающихся плоскостей.
3. Перпендикулярность плоскостей: две плоскости взаимно
перпендикулярны, если одна из них содержит перпендикуляр к
другой. Прямая перпендикулярная плоскости называется нормаль
плоскости и перпендикулярна двум пересекающимся прямым,
лежащим в этой плоскости.
13
14. Взаимное положение плоскостей Параллельные плоскости
Пример 2Пример 1
К2
а2
а2
М2
b2
m2
m2
К2
l2
К1
а1
b1
М1
m1
М2
b2
М1
h2
h1
b1
l1
К1
m1
а1
14
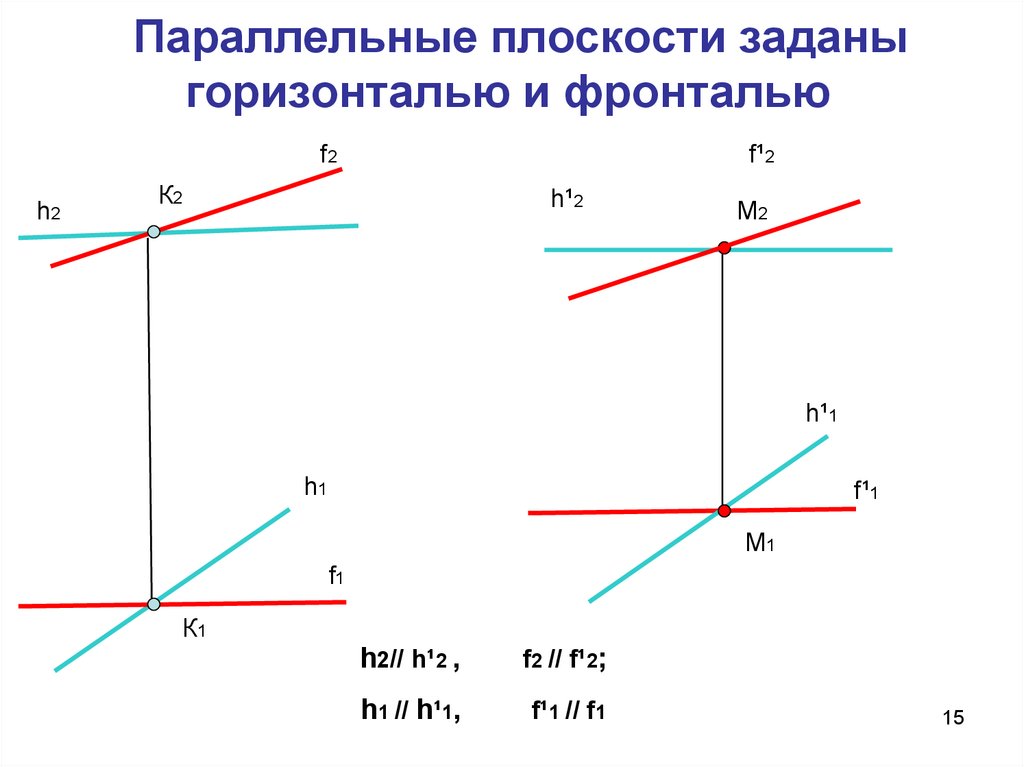
15. Параллельные плоскости заданы горизонталью и фронталью
f2h2
f¹2
К2
h¹2
M2
h¹1
h1
f¹1
M1
f1
К1
h2// h¹2 ,
f2 // f¹2;
h1 // h¹1,
f¹1 // f1
15
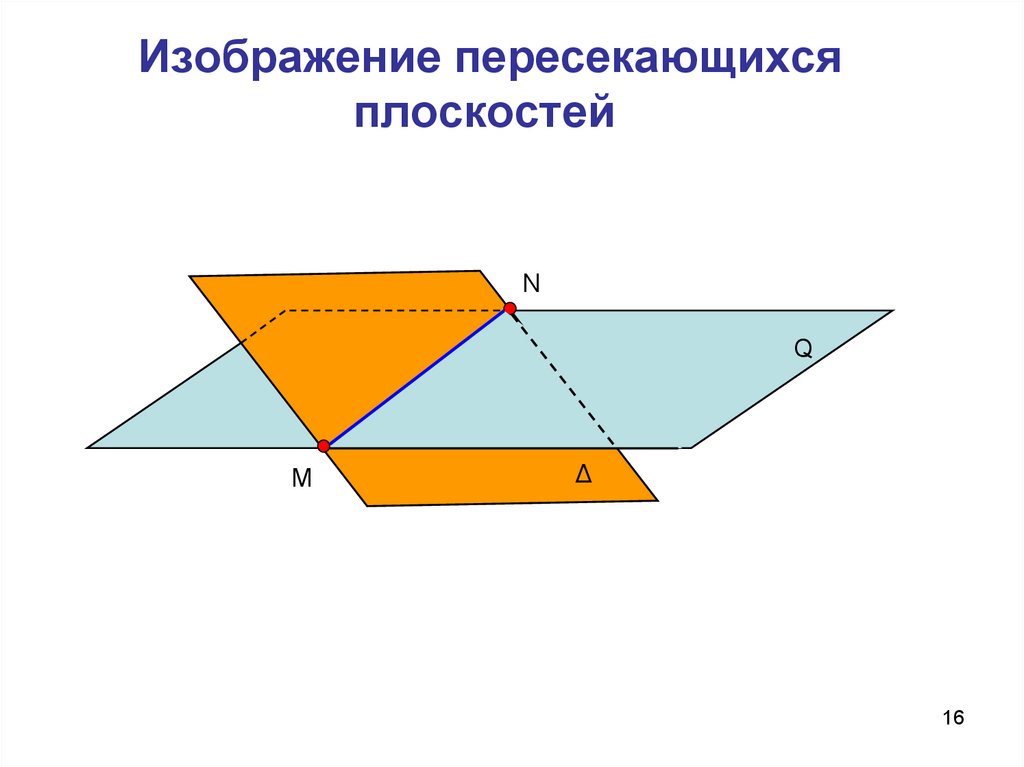
16. Изображение пересекающихся плоскостей
NQ
M
Δ
16
17.
Изображение перпендикулярныхплоскостей
N2
N
f2
Q
h2
A2
А
h
Δ
Х
f
h1
A1
Δ( h∩f) Q ( N h, N f )
f1
N1
17









 Инженерная графика
Инженерная графика








