Похожие презентации:
Math relation and function
1.
MATHRELATION AND FUNCTION
by TULEGENOVA KAMSHAT
2.
3.
4.
OutlineIntroduction to relation
Introduction to function/Types of functions
Domain and range
x and y intercept
5.
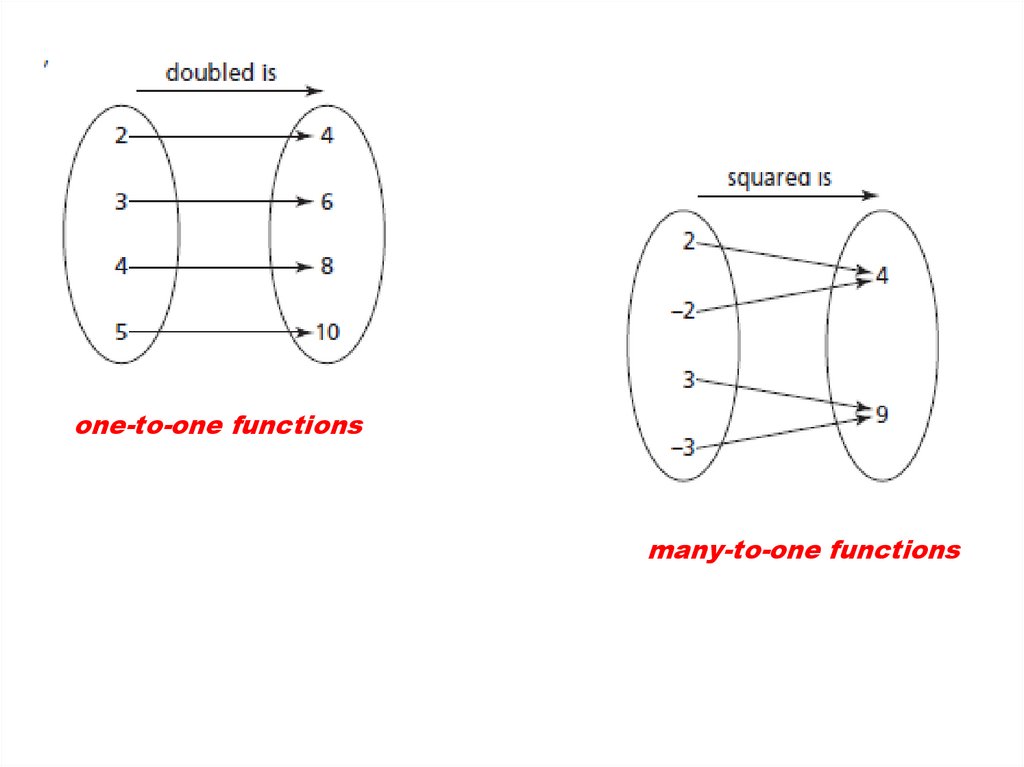
A function is a special type ofrelation where each element in
the one set is
associated with exactly one
element in the other set.
6.
one-to-one functionsmany-to-one functions
7.
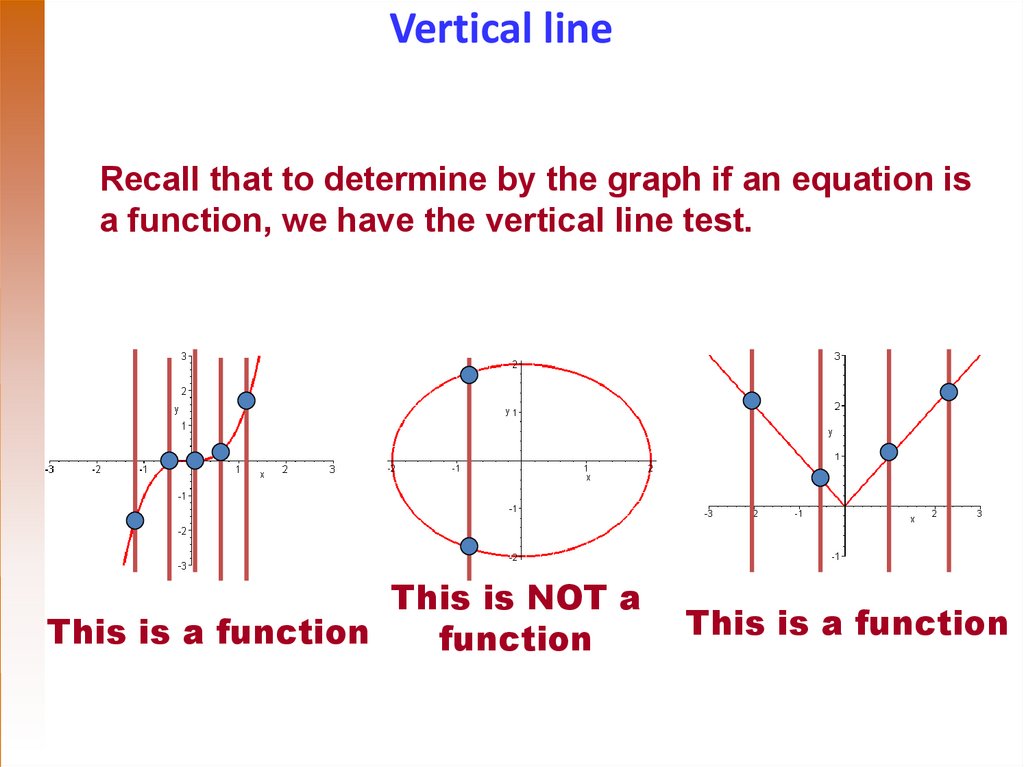
Vertical lineRecall that to determine by the graph if an equation is
a function, we have the vertical line test.
This is NOT a
This is a function
function
This is a function
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
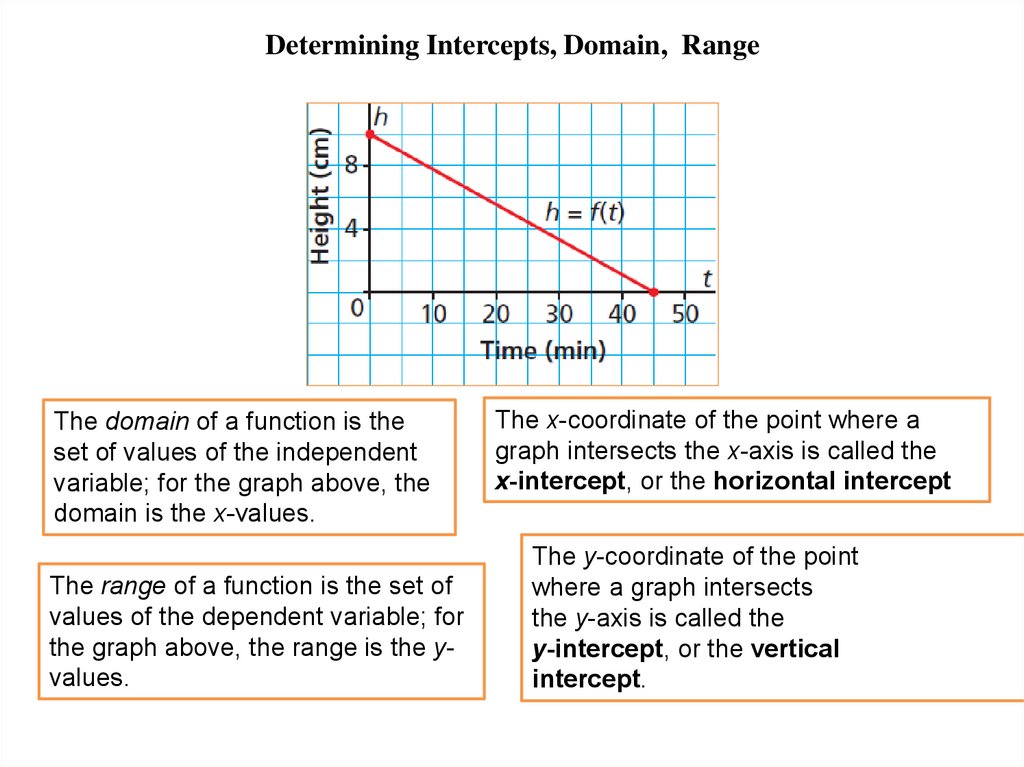
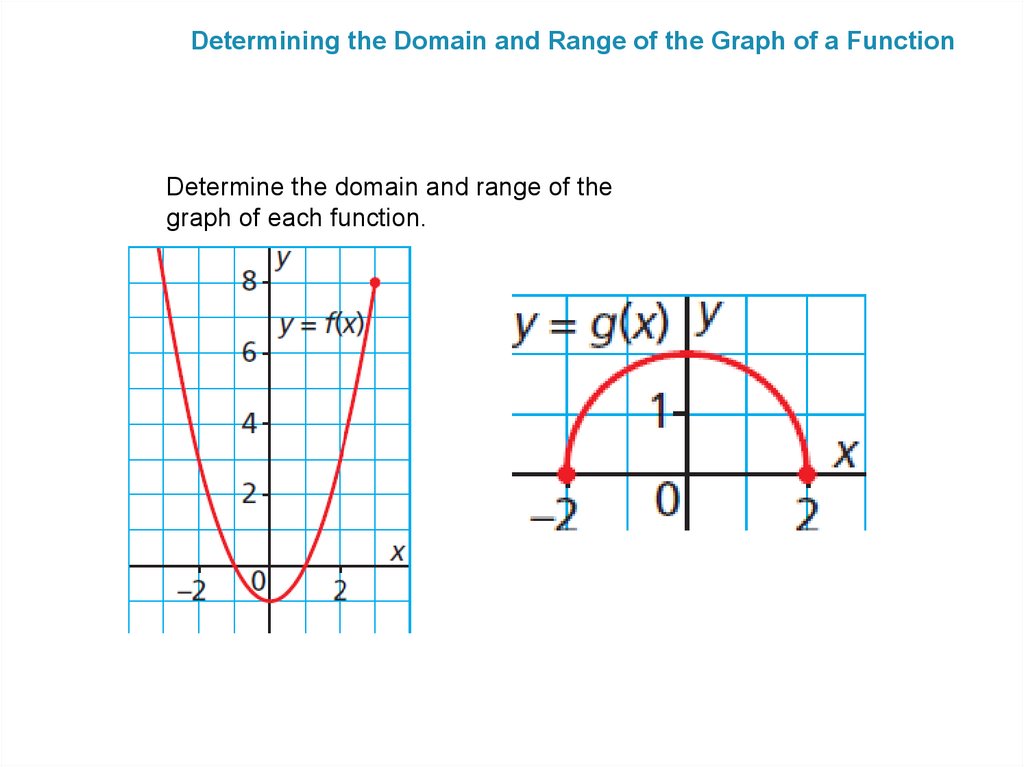
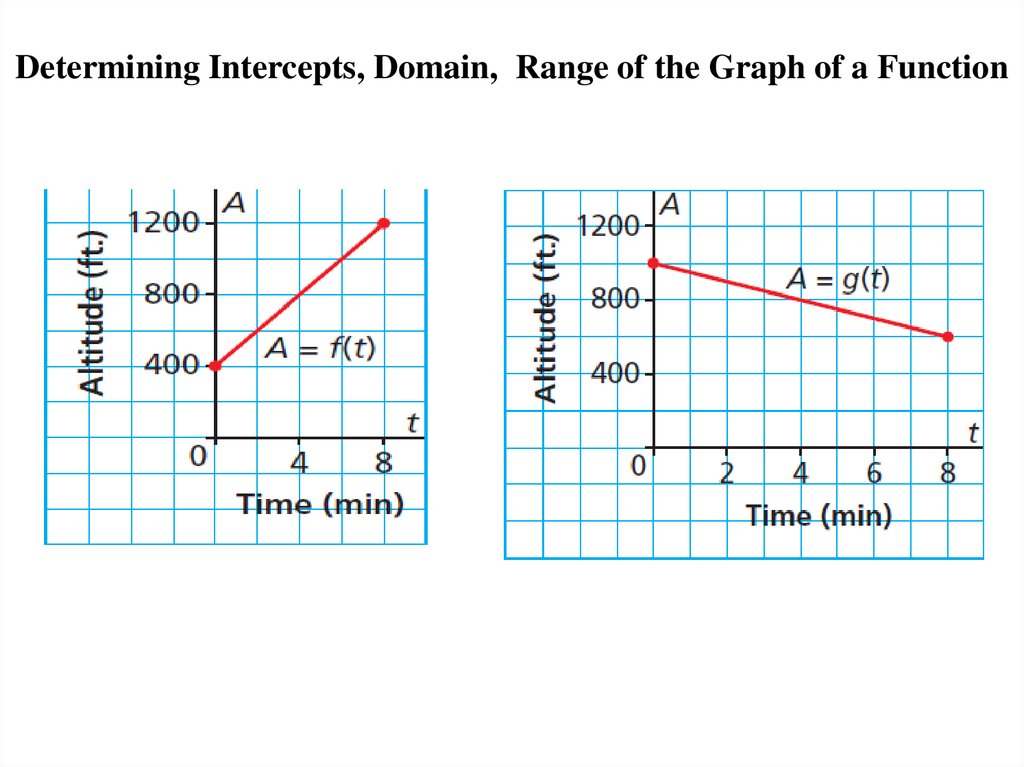
Determining Intercepts, Domain, RangeThe domain of a function is the
set of values of the independent
variable; for the graph above, the
domain is the x-values.
The range of a function is the set of
values of the dependent variable; for
the graph above, the range is the yvalues.
The x-coordinate of the point where a
graph intersects the x-axis is called the
x-intercept, or the horizontal intercept
The y-coordinate of the point
where a graph intersects
the y-axis is called the
y-intercept, or the vertical
intercept.
18.
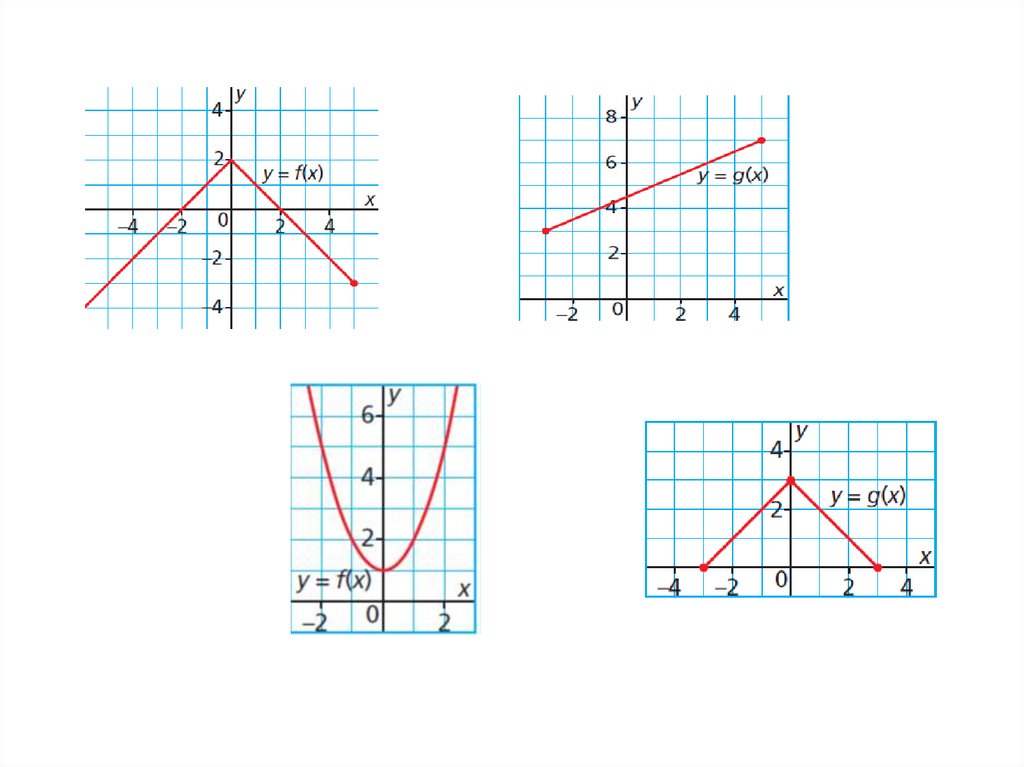
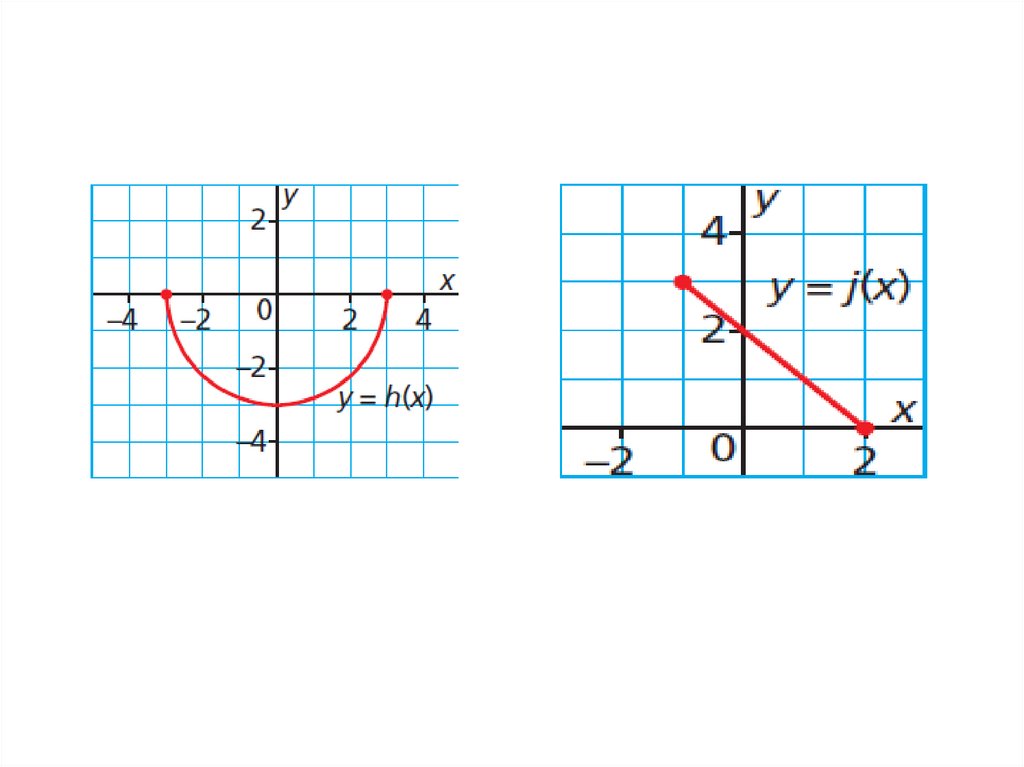
Determining the Domain and Range of the Graph of a FunctionDetermine the domain and range of the
graph of each function.
19.
20.
21.
Determining Intercepts, Domain, Range of the Graph of a Function22.
23.
Even functionsIf a function is such that f(–x) = f(x) for all values
of x, it is called an even function.
For example, show that f(x) = 3x4 – x2 + 2
is an even function.
f(–x) = 3(–x)4 – (–x)2 + 2
= 3x4 – x2 + 2
= f(x)
f(–x) = f(x), so the function is even.
Can you write down another even function?
24.
Graphs of even functionsHere are the graphs of some even functions:
y
y
y
x
x
x
What do you notice about these graphs?
The graphs of all even functions are
symmetric about the y-axis.
25.
Odd functionsIf a function is such that f(–x) = –f(x) for all values
of x, it is called an odd function.
For example, show that f(x) = x3 + 4x is
an odd function.
f(–x) = (–x)3 + 4(–x)
= –x3 – 4x
= –(x3 + 4x)
= –f(x)
f(–x) = –f(x), so the function is odd.
Can you write down another odd function?
26.
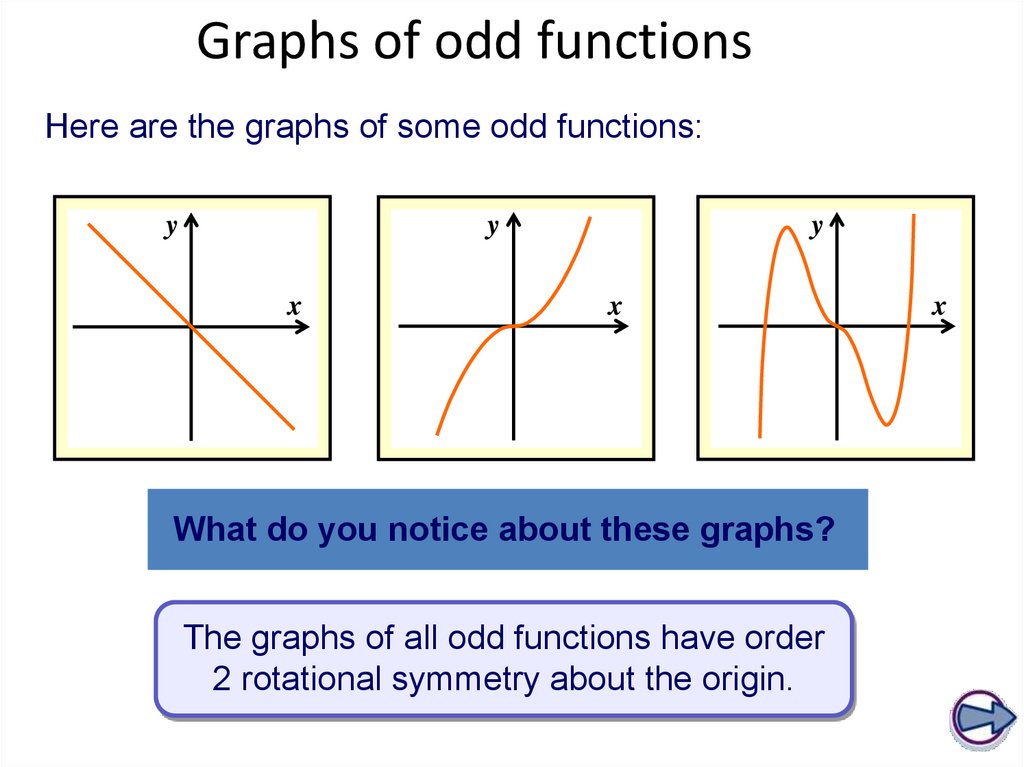
Graphs of odd functionsHere are the graphs of some odd functions:
y
y
x
y
x
What do you notice about these graphs?
The graphs of all odd functions have order
2 rotational symmetry about the origin.
x
27.
28.
29.
30.
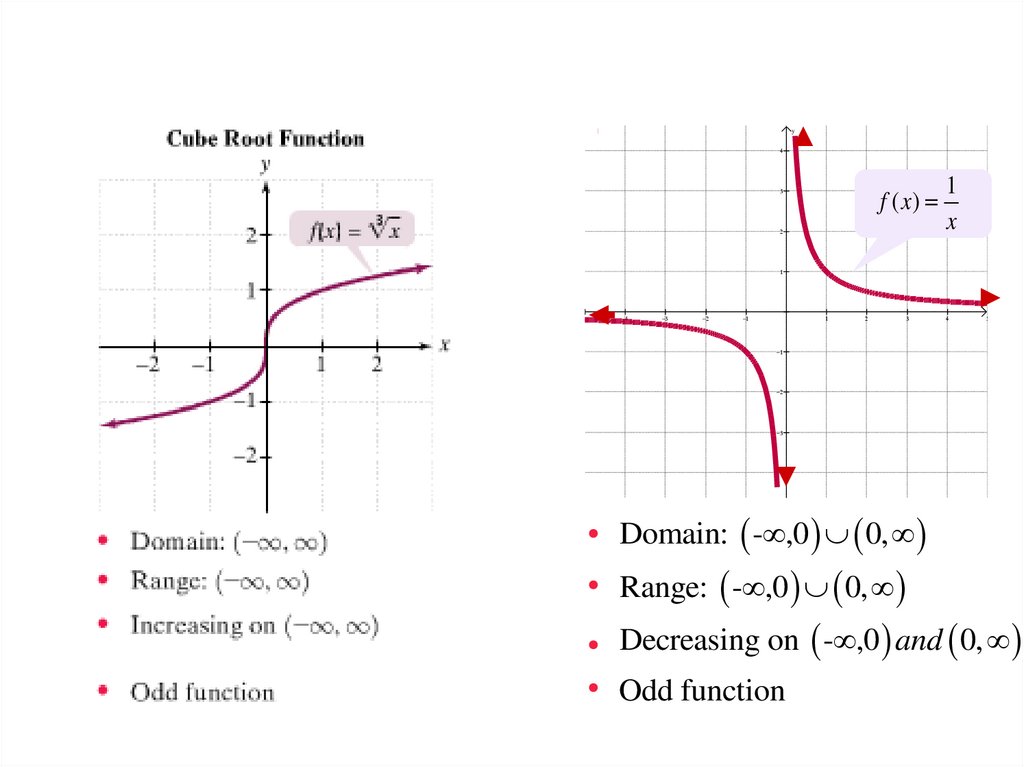
Reciprocal Functiony
f ( x)
1
x
x
Domain: - ,0 0,
Range: - ,0 0,
Decreasing on - ,0 and 0,
Odd function
31.
32.
Literature1.
https://byjus.com/maths/rational-function/
2. https://www.analyzemath.com/rational/rational1.html
3. https://oregonstate.edu/instruct/mth251/cq/FieldGuide/rational/less
on.html
















 Математика
Математика








