Похожие презентации:
Параллельные прямая и плоскость. Параллельные плоскости. Определение. Признак. Свойства
1.
Государственное автономное профессиональноеобразовательное учреждение
«Липецкий медицинский колледж»
Преподаватель: Дедова Т.А
2024
2.
Цель:разобрать понятие параллельных прямых и
плоскостей. Дать определение, доказать признак и
рассмотреть свойства. Научиться применять
данный материал в решении задач
3.
Определение параллельныхпрямых
Параллельные прямые – прямые, которые
лежат в одной плоскости и не пересекаются.
4.
Признак параллельности прямыхДве прямые, параллельные третьей,
параллельны между собой.
5.
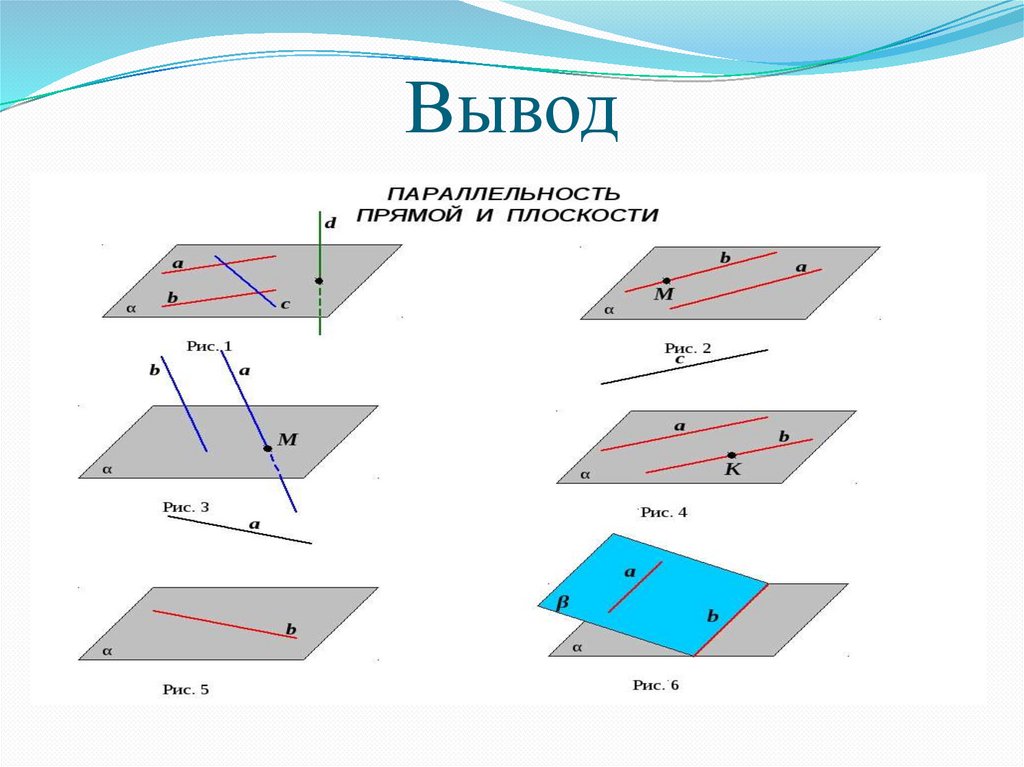
Параллельные прямая и плоскостьПрямая и плоскость называются параллельными, если
они не имеют общих точек.
6.
Признак параллельности прямойи плоскости
Если прямая, не принадлежащая данной плоскости,
параллельна какой-нибудь прямой этой плоскости, то
она параллельна этой плоскости.
7.
Свойство прямой, параллельной даннойплоскости
Если плоскость β проходит через прямую a,
параллельную плоскости α, и пересекает эту
плоскость по прямой b, то b || a.
8.
Определение параллельныхплоскостей
Параллельные плоскости –
плоскости, которые не
пересекаются.
9.
Признаки параллельностиплоскостей
Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум пересекающимся
прямым другой плоскости, то такие плоскости
параллельны.
10.
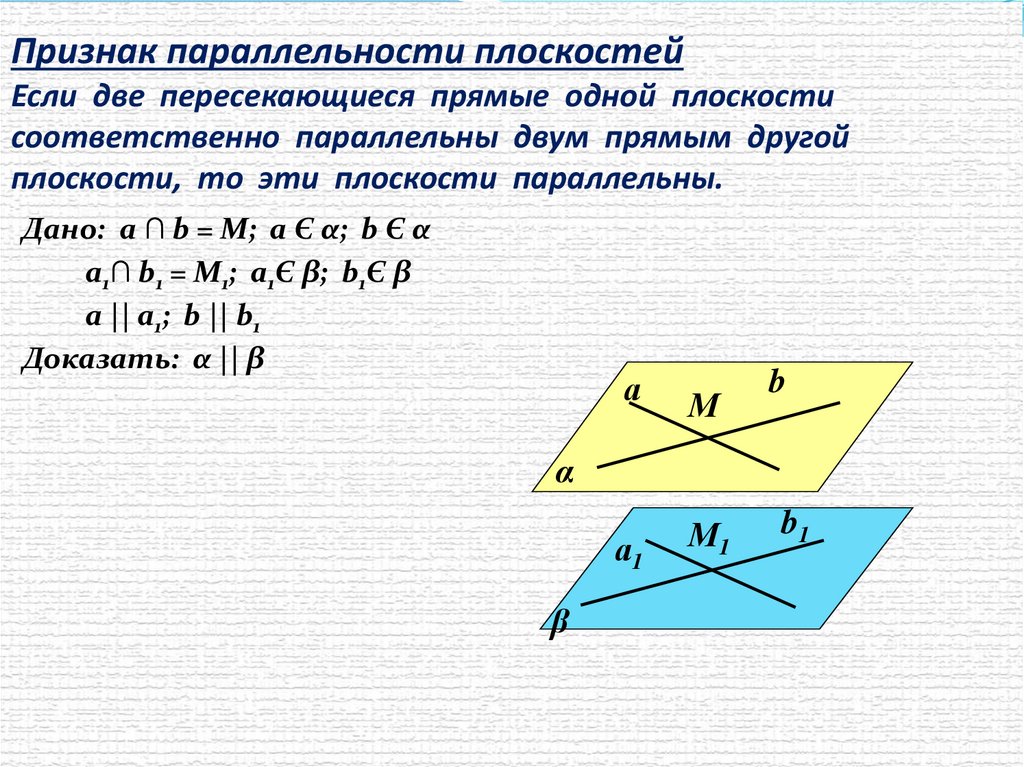
Признак параллельности плоскостейЕсли две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
Дано: а ∩ b = М; а Є α; b Є α
а1∩ b1 = М1; а1Є β; b1Є β
a || a1; b || b1
Доказать: α || β
а
М
а1
М1
b
α
β
b1
11.
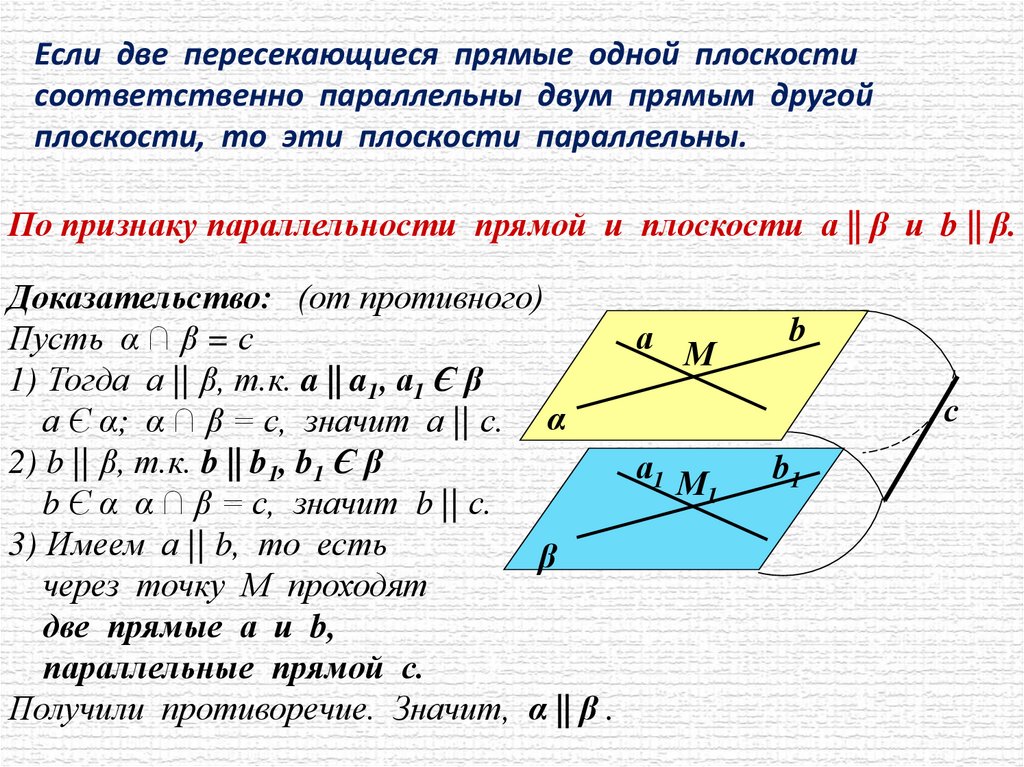
Если две пересекающиеся прямые одной плоскостисоответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
По признаку параллельности прямой и плоскости а || β и b || β.
Доказательство: (от противного)
а М
Пусть α ∩ β = с
1) Тогда а || β, т.к. a || a1, а1 Є β
а Є α; α ∩ β = с, значит а || с. α
2) b || β, т.к. b || b1, b1 Є β
а1 М
1
b Є α α ∩ β = с, значит b || с.
3) Имеем а || b, то есть
β
через точку М проходят
две прямые а и b,
параллельные прямой с.
Получили противоречие. Значит, α || β .
b
с
b1
12.
Признаки параллельностиплоскостей
Если каждая из двух данных плоскостей параллельна
третьей плоскости, то данные две плоскости
параллельны между собой.
13.
Свойства параллельныхплоскостей
Если две параллельные плоскости пересекаются
третьей плоскостью, то линии пересечения
плоскостей параллельны.
14.
Свойства параллельныхплоскостей
Отрезки параллельных прямых, заключенные
между двумя параллельными плоскостями, равны.
15.
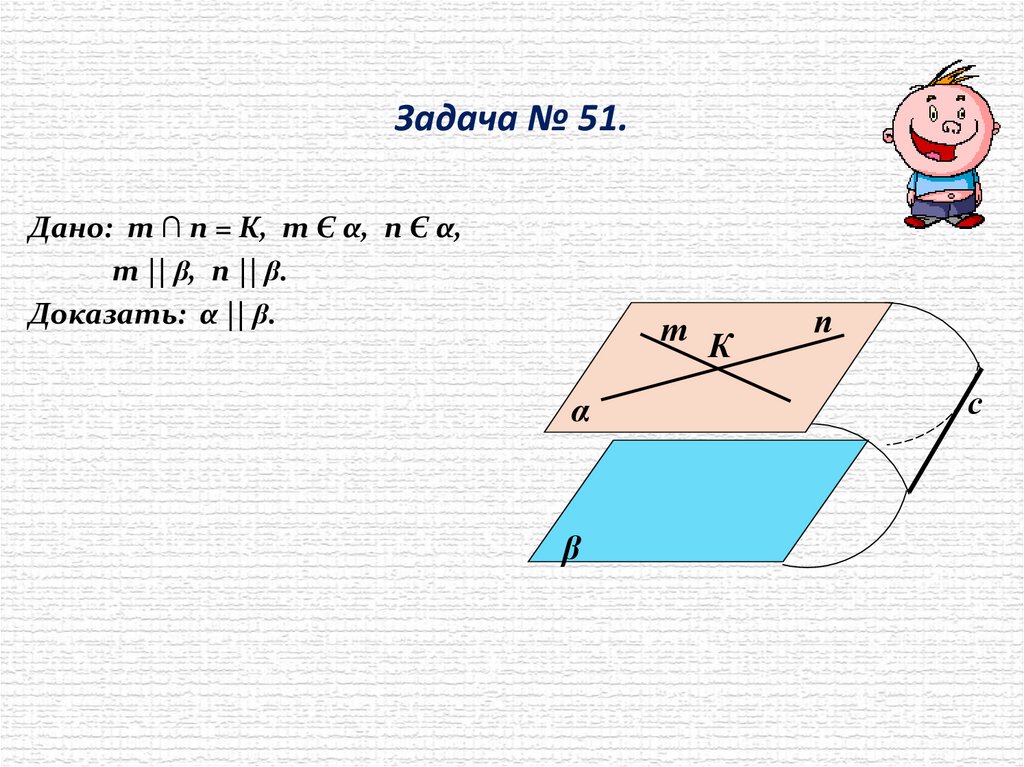
Задача № 51.Дано: т ∩ n = К, т Є α, n Є α,
т || β, n || β.
Доказать: α || β.
т К
α
β
п
с
16.
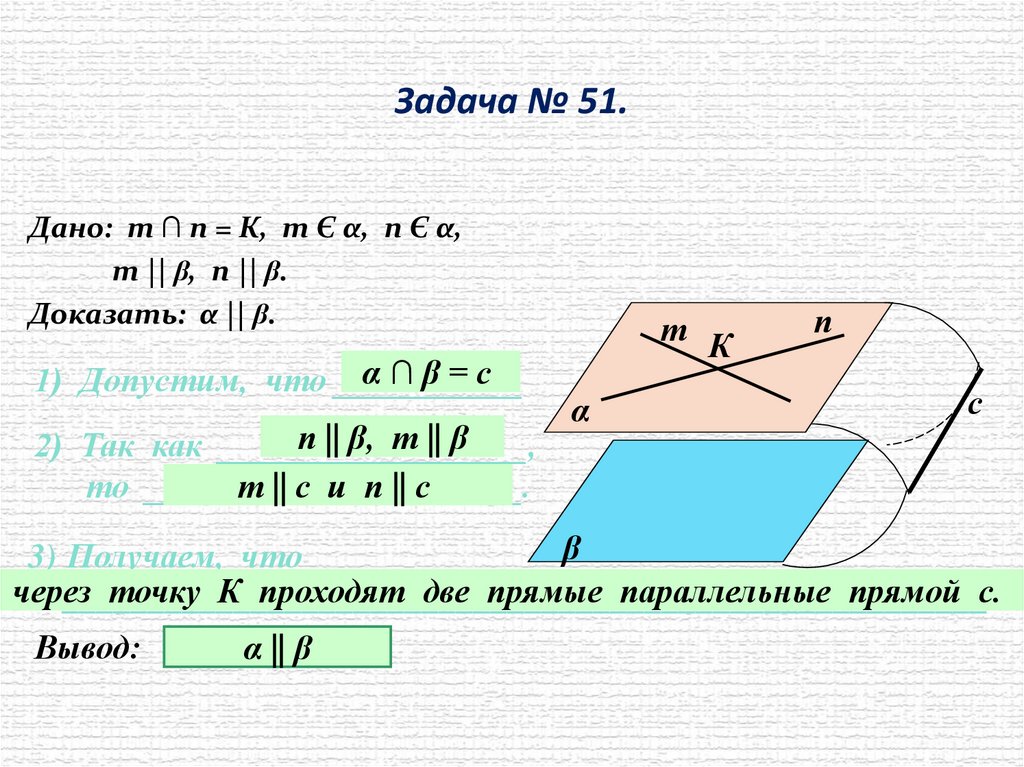
Задача № 51.Дано: т ∩ n = К, т Є α, n Є α,
т || β, n || β.
Доказать: α || β.
α∩β=с
1) Допустим, что ___________
п || β, т || β
2) Так как __________________,
т || с и п || с
то ______________________.
т К
α
п
с
β
3) Получаем, что
через
точку К проходят две прямые параллельные прямой с.
______________________________________________________.
Вывод:
α || β
17.
Проверка знанийМогут ли прямая и плоскость не иметь общих
точек?
Да
Нет
Верно ли, что если две прямые не пересекаются,
то
они параллельны?
Плоскости α и β параллельны, прямая n лежитДа
в
плоскости α. Верно ли, что прямая n параллельна
плоскости β?
Верно ли, что если прямая а параллельна одной из
двух параллельных плоскостей, с другой Нет
плоскостью прямая а имеет одну общую точку?
Верно ли, что плоскости параллельны, если Нет
прямая, лежащая в одной плоскости, параллельна
другой плоскости?
18.
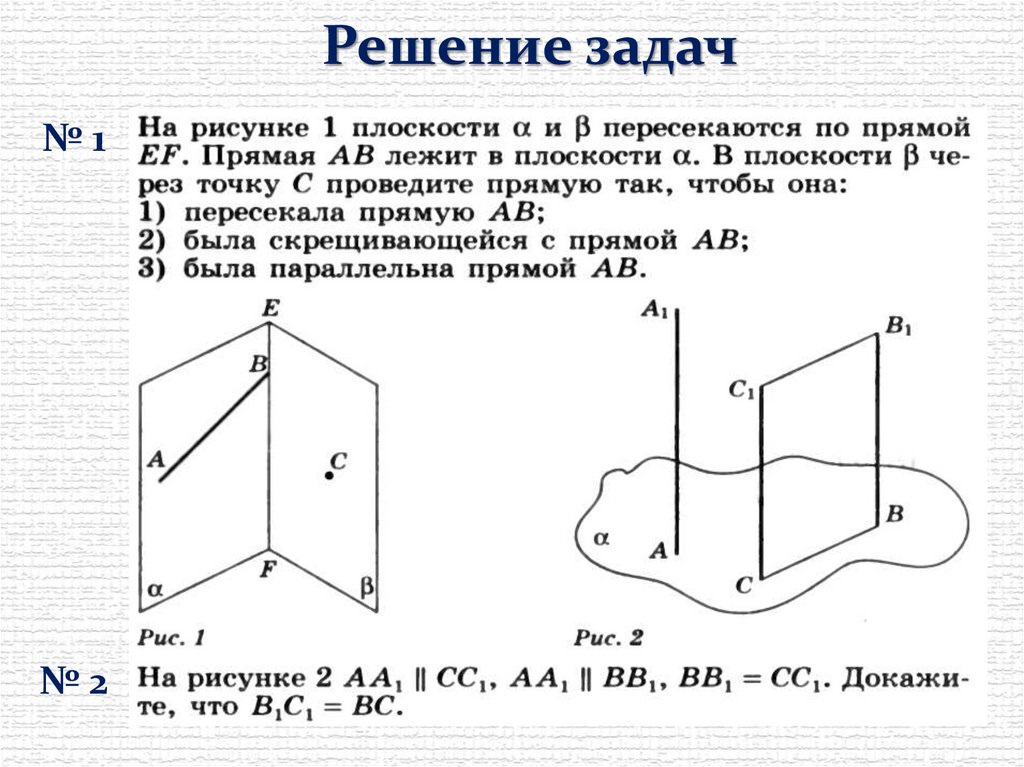
Решение задач№1
№2
19.
Решение задач№3
№4
20.
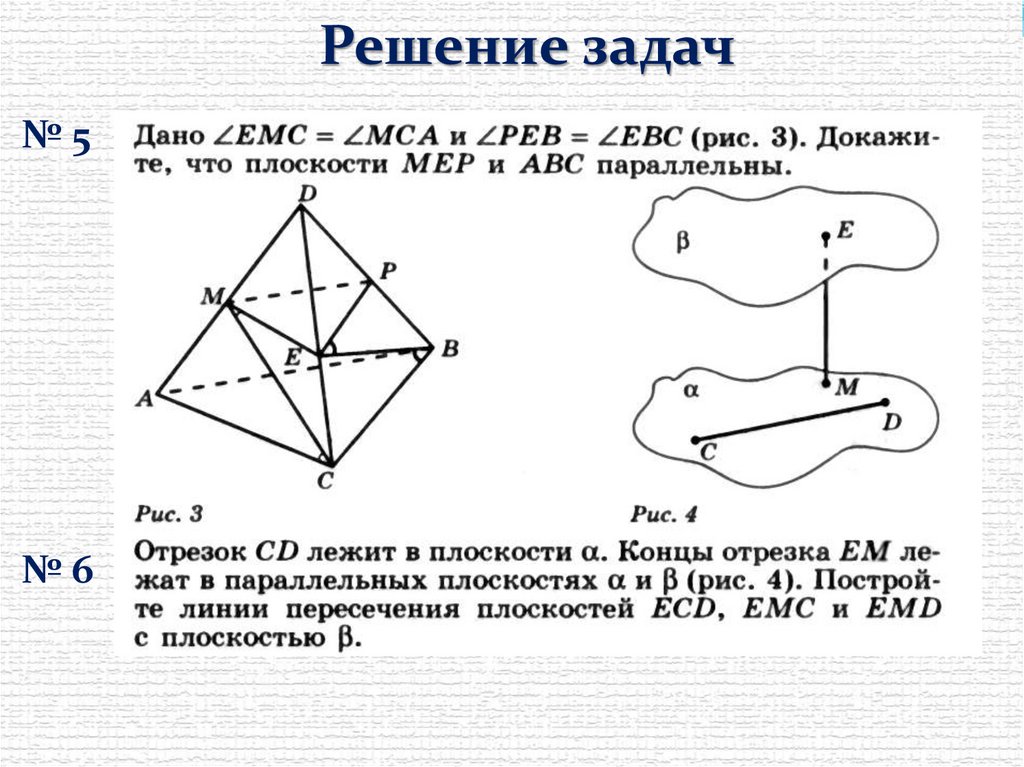
Решение задач№5
№6
21.
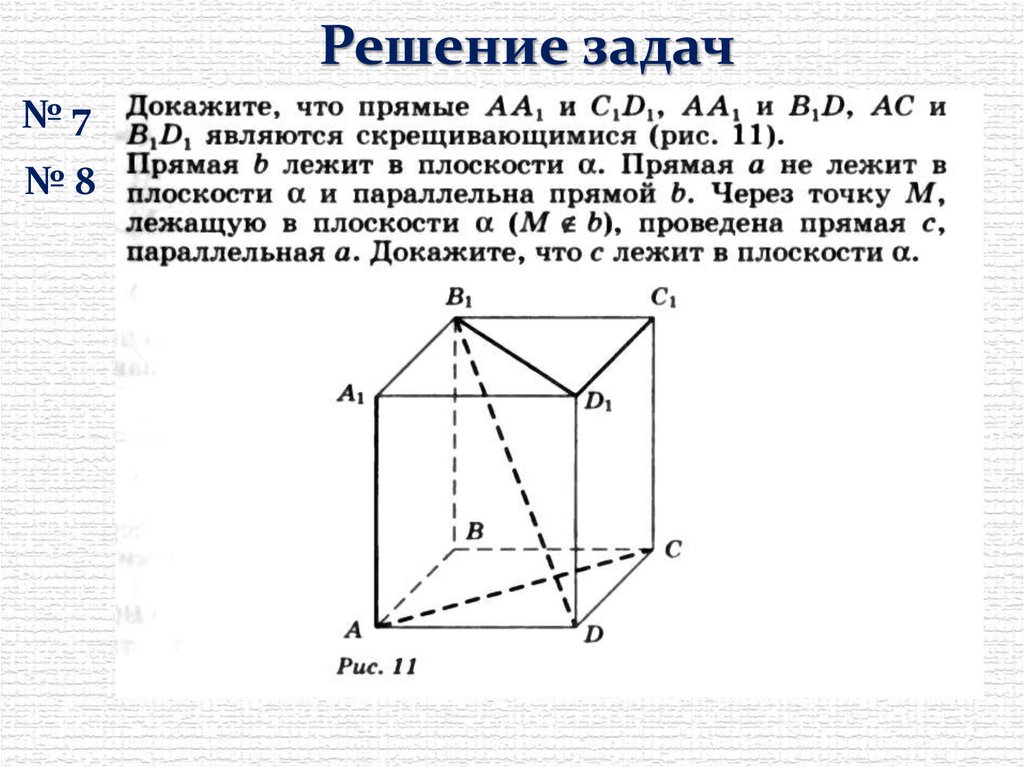
Решение задач№7
№8
22.
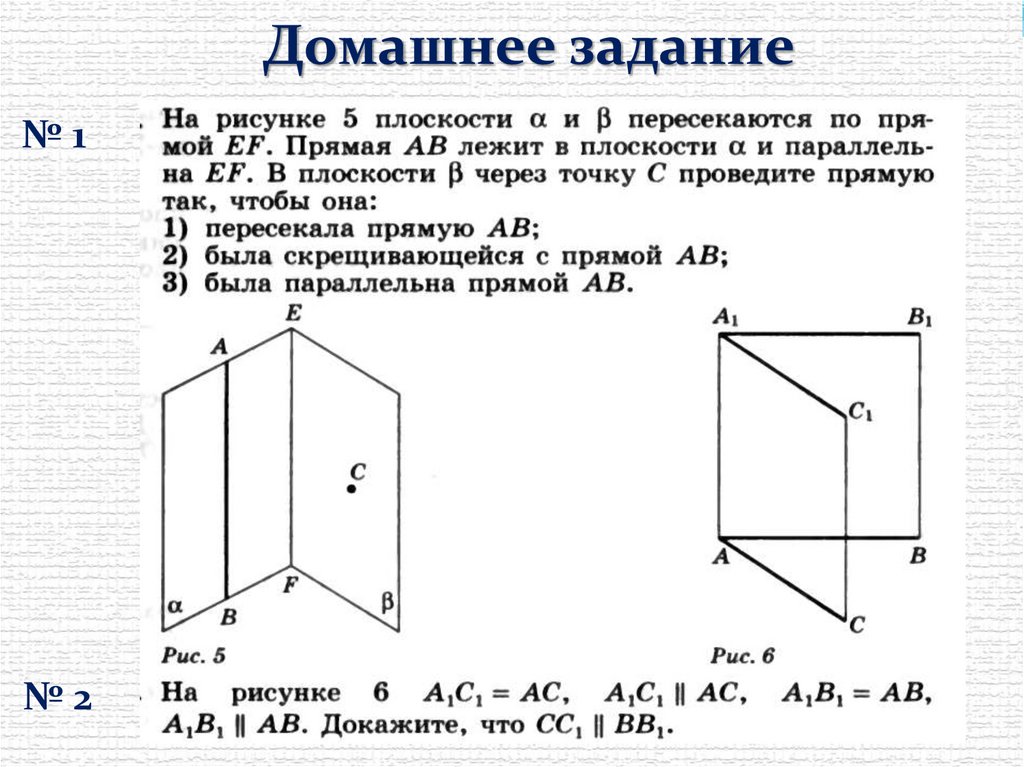
Домашнее задание№1
№2
23.
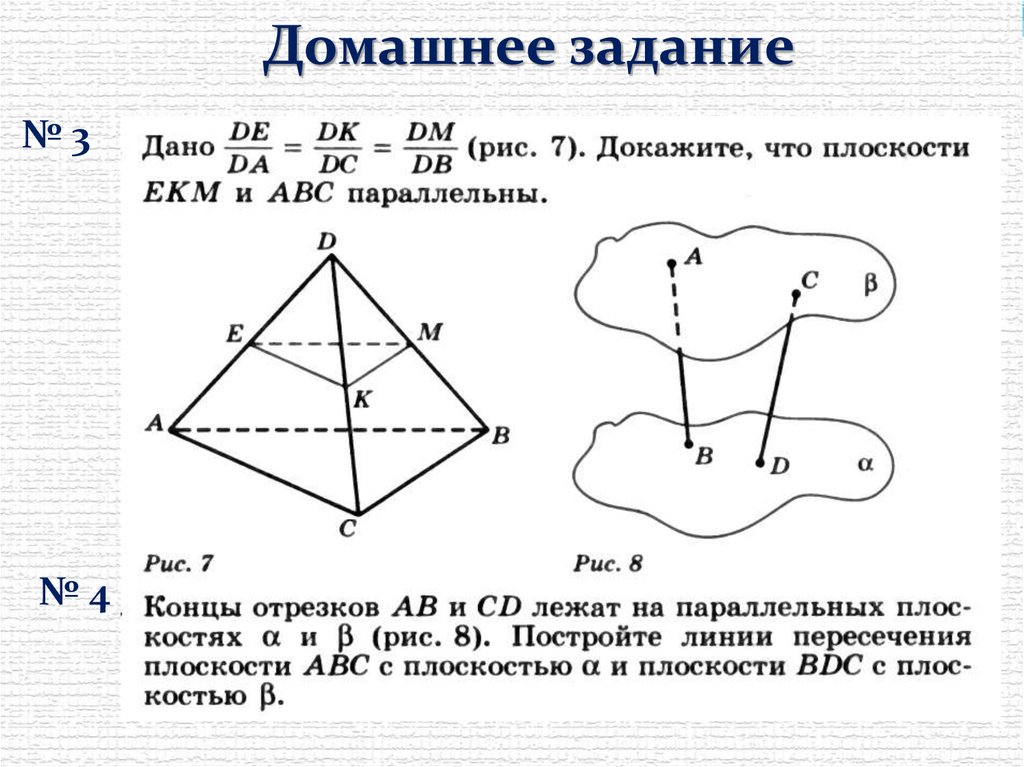
Домашнее задание№3
№4















 Математика
Математика








