Негізгі позициялық есептер

1.

Негізгі позициялық есептер
5-тәжірибелік сабақ
Қарымсақов Уалихан Төленұлы

2.

Проекция
Проекция
Projection
Нүкте
Точка
Point
Түзу
Прямая
Straight Line
Жазықтық
Плоскость
Plane
Қиылысу
Пересечение
Intersect
Өзара орналасуы
Взаимное
расположение
Mutual Positions
Бәсекелес
нүктелер
Конкурирующие
точки
Competing points

3.

Негізгі позициялық есептер деп
нүктелердің, түзулердің және
жазықтықтардың өзара орналасуын
анықтауға арналған есептерді айтамыз.

4.

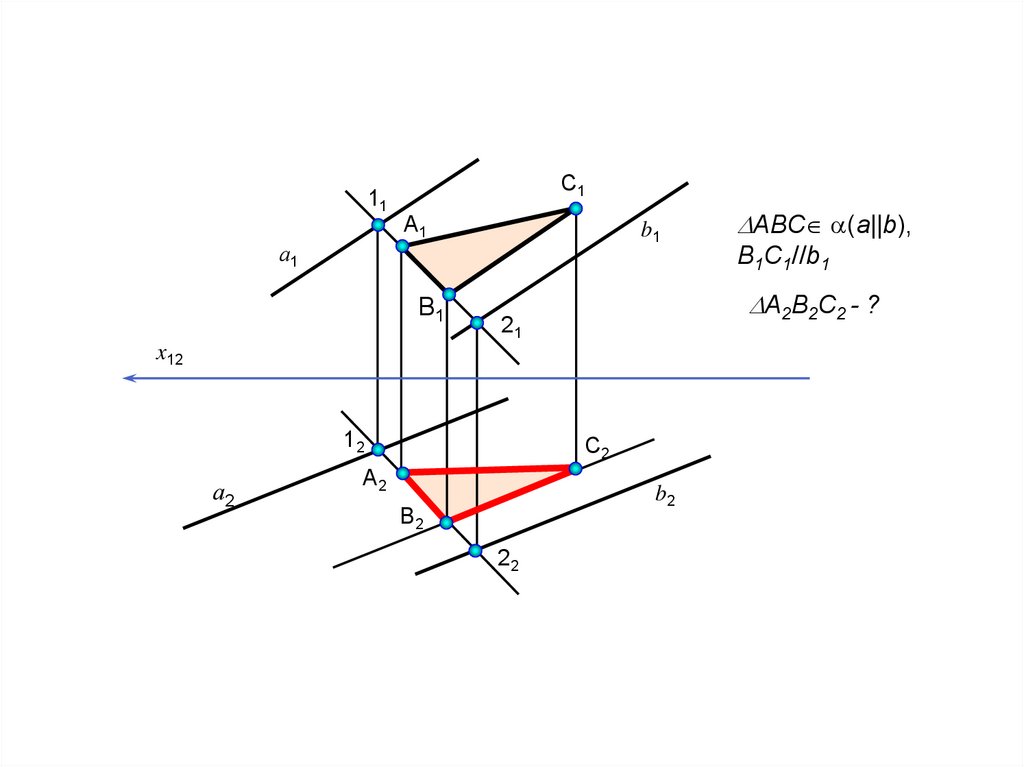
11
а1
С1
А1
b1
B1C1//b1
В1
A2B2C2 - ?
21
x12
12
а2
ABC (a||b),
С2
А2
b2
В2
22

5.

ABCDE көпбұрышының горизонталь проекциясын аяқтау керек
B1
В1
С1
А1
11
А1
С1
21
D1
E1
х12
E1
D1
С2
B2
А2
С2
12
А2
22
E2
D2
D2

6.

В1
11
А1
х12
f1
h1
21
С1
А2
f2
В2
22
12
h2
С2
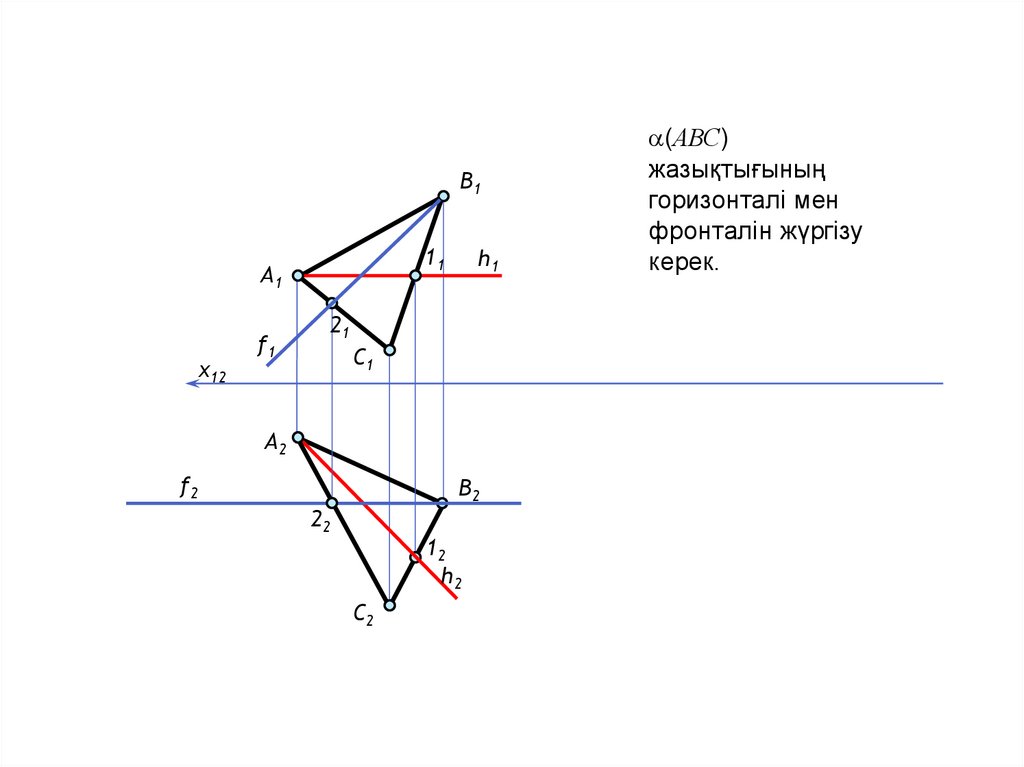
(АВС)
жазықтығының
горизонталі мен
фронталін жүргізу
керек.

7.

(a||b)
a1
11
h1
жазықтығының
горизонталі мен
фронталін жүргізу
керек.
b1
21
х12
b2
h2
a2
12
22

8.

Проекциялаушы түзудің жалпы жағдай
жазықтығымен қиылысуы
l 2

9.

S
10
20
50
A
60
15
65
B
45
60
20
C
0
40
10
1.
S нүктесі арқылы (АВС)
жазықтығына параллель горизонталь
түзу салу керек.
A1
m1
S m
S1 m1|| h1
S2 m2|| h2
h (ABC)
m||
S1
11
h1
B1
x
C1
O
A2
h2
S2
12
B2
C2

10.

. Жалпы жағдайдағы түзудің жалпы
жағдайдағы жазықтықпен қиылысуы.
m
C
21
l1
3
1
1
K
A1
1
1
x1
1
41=
51
B
1
1
2
A
K2 2
2
2
l2 2
l2=g2=m
С2
52
12
12=3
2
42
B2
Көрінетіндікті анықтау.
1. Берілген l түзуі арқылы горизонтальпроекциялаушы жазықтығын жүргіземіз.
2. Көмекші жазықтығының жазықтығымен
қиылысу сызығы m түзуін жүргіземіз: m=( ∩ ).
m және l түзулері горизонталь-проекциялаушы
жазықтығында жатады, яғни горизонталь
бәсекелес болып табылады, сондықтан: l2= 2=m2.
m2∩(A2B2)=12.
m2∩(A2C2)=22.
12 11 (A1B1).
22 21 (A1C1).
(11 21)=m1.
3. a) m1 =l1 l ;
ә) m1 | | l1 l | | ;
б) m1 ∩ l1 l ∩ .
1 (AB), 3 l
1 және 3 нүктелері – горизонталь-бәсекелес.
3 нүктесі биік орналасқан, сондықтан горизонталь проекцияда l
түзуінің K2 мен 22 нүктелерінің арасы көрінбейді.
4 l, 5 (BС)
4 және 5 нүктелері – фронталь-бәсекелес.
5 нүктесі жақын орналасқан, сондықтан фронталь проекцияда l
түзуінің K1 мен 41 нүктелерінің арасы көрінбейді.
(m1 ∩ l1 ) =K1.
K1 K2 l2.
K=(l∩ ).

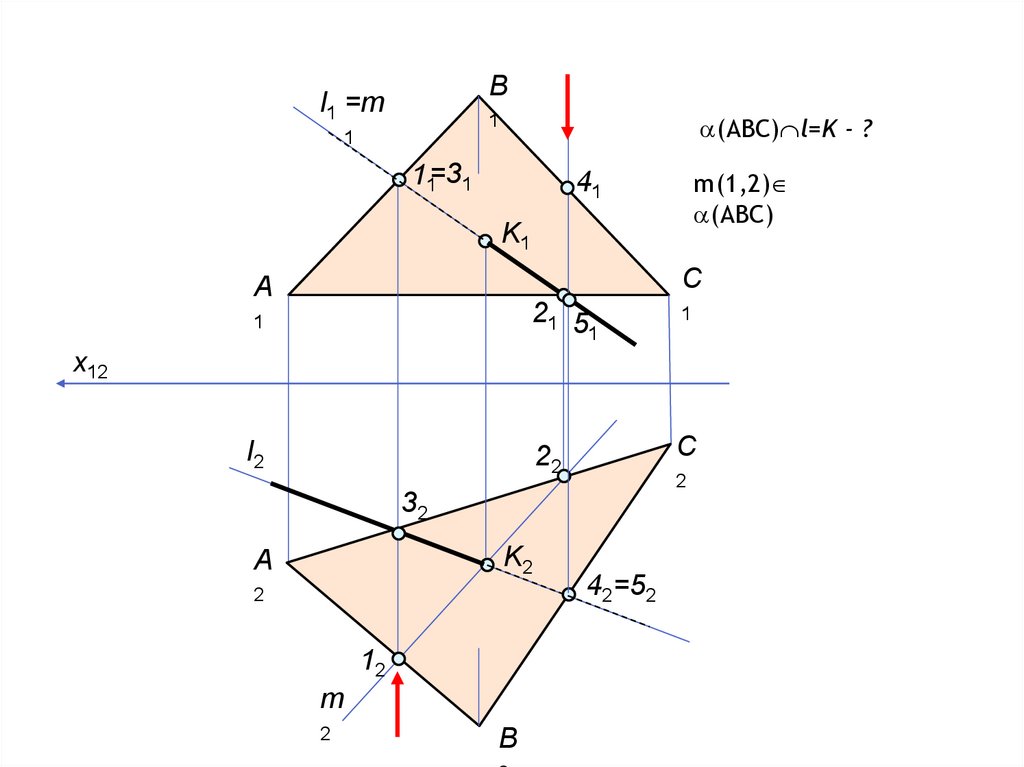
11.

B
l1 =m
(ABC) l=K - ?
1
1
11=31
m(1,2)
(ABC)
41
K1
C
A
1
21 5
l2
22
1
1
x12
C
2
32
K2
A
2
12
m
2
B
42=52

12.

B
1
11
(ABC), K
К1
K (ABC) - ?
A
1
K (ABC)
C
1
C
A
2
2
12
К2
B
2

13.

Екі жазықтықтың қиылысу сызығын салу
Қиылысатын екі жазықтық та жалпы жағдайда орналасқанда олардың қиылысу сызығын салу үшін
көмекші жазықтықтар әдісін қолданамыз. Жалпы жағдайдағы (АВС) және (m//n) жазықтықтары
берілген. Жазықтықтардың қиылысу сызығының екі ортақ нүктелерін анықтау үшін көмекші және
проекциялаушы жазықтықтарын енгіземіз.
В1 l 1
M1
11
1 = a 1 = c1
m1
21
N1
1 = b1= d1 A1
n1
31
41
61
(ABC)
71
(m n)
51
С1
x1
2
1
a2
В2
12
32
72
22 M2
52
С2
l2
d2
42
b2
A2
=a
c2
62
N2
m2
n2
=c
a c=M
1
=b
=d
b d=N
M2 N2=l2
M1 N1=l1

14.

•Өзара қиылысатын (АВС) және (DEF) жазықтықтарының қиылысу сызығын анықтайтын M, N
нүктелерінің әрқайсысы АВС және DEF үшбұрыштарының біреуінің кез келген қабырғасының екінші
үшбұрышпен қиылысу нүктесі ретінде табылады. Сонда екі рет түзу мен жазықтықтың қиылысу
нүктесін анықтау есебі шешіледі.
(ABC)
E1 51=61 B1
31
A1
N1
41
F1
11
2
42
62
(DE) ,
N2
32
D2
12
B2
1
C2
(ABC)=(34)
22=72
(34) (DE)=N
M1 N1
M2
52
2
(DEF)=(12)
(12) (BC)=M
C1
E2
A2
(BC) ,
71
D1
x1
(ABC) (DEF)=(MN)
21
M1
(DEF)
F2
M2 N2

15.

n1
31
D1
21
C1
A1
M1
11
F1
m1
N1
B1
41
E1
x12
O1
F2
42
2
1
m
2
E2
2
M2
C2
N2
3
2
2
n2
B2
A2
D2