Перпендикулярность прямых и плоскостей. Перпендикуляр и наклонные. Теорема о трех перпендикулярах

1. Перпендикулярность прямых и плоскостей

Перпендикуляр и наклонные
Теорема о трех перпендикулярах

2. Перпендикуляр и наклонные

М α
МН α
Н α
А α
В α
М
α
Н
А
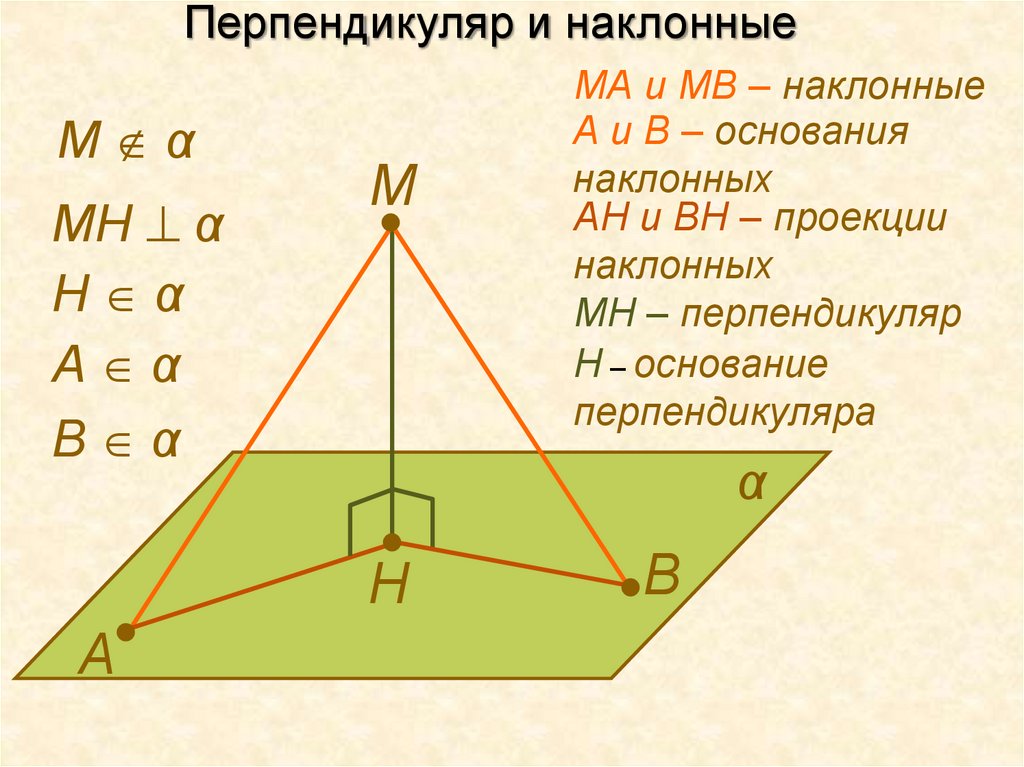
МА и МВ – наклонные
А и В – основания
наклонных
АН и ВН – проекции
наклонных
МН – перпендикуляр
H – основание
перпендикуляра
В

3.

NB!
Перпендикуляр, проведенный из данной
точки к плоскости, меньше любой
наклонной, проведенной из той же точки к
этой плоскости.
Расстоянием от точки до плоскости
называется длина перпендикуляра,
проведенного из точки к этой плоскости

4.

Замечание 1.
β
α
А
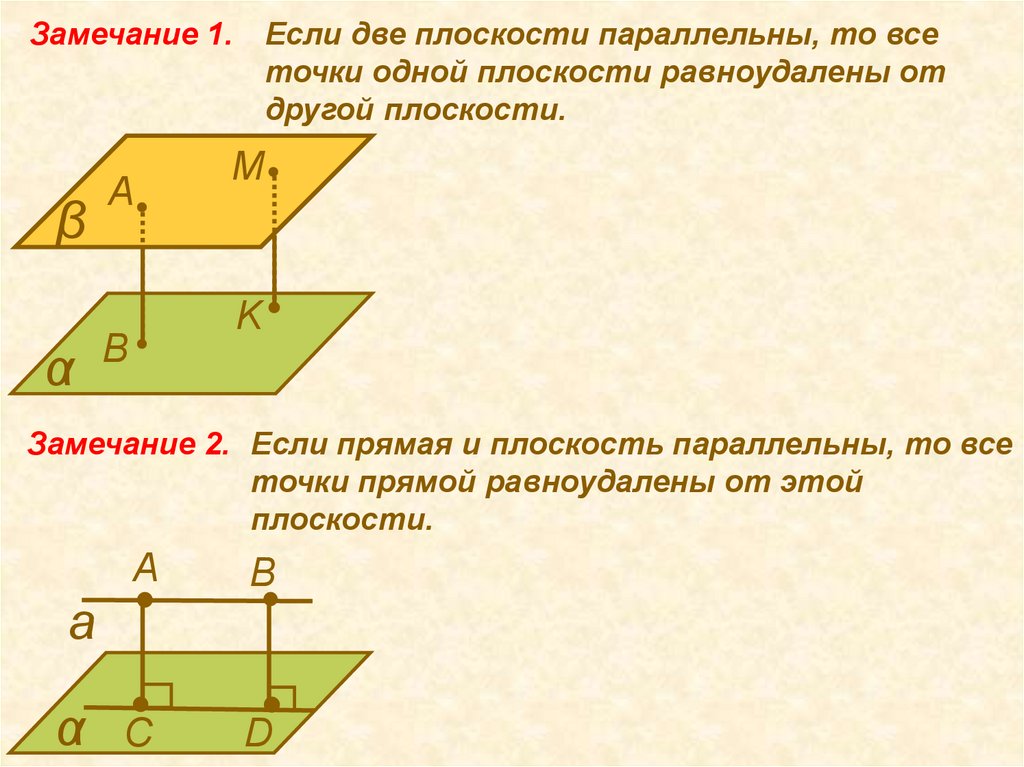
Если две плоскости параллельны, то все
точки одной плоскости равноудалены от
другой плоскости.
M
K
B
Замечание 2. Если прямая и плоскость параллельны, то все
точки прямой равноудалены от этой
плоскости.
А
B
C
D
а
α

5.

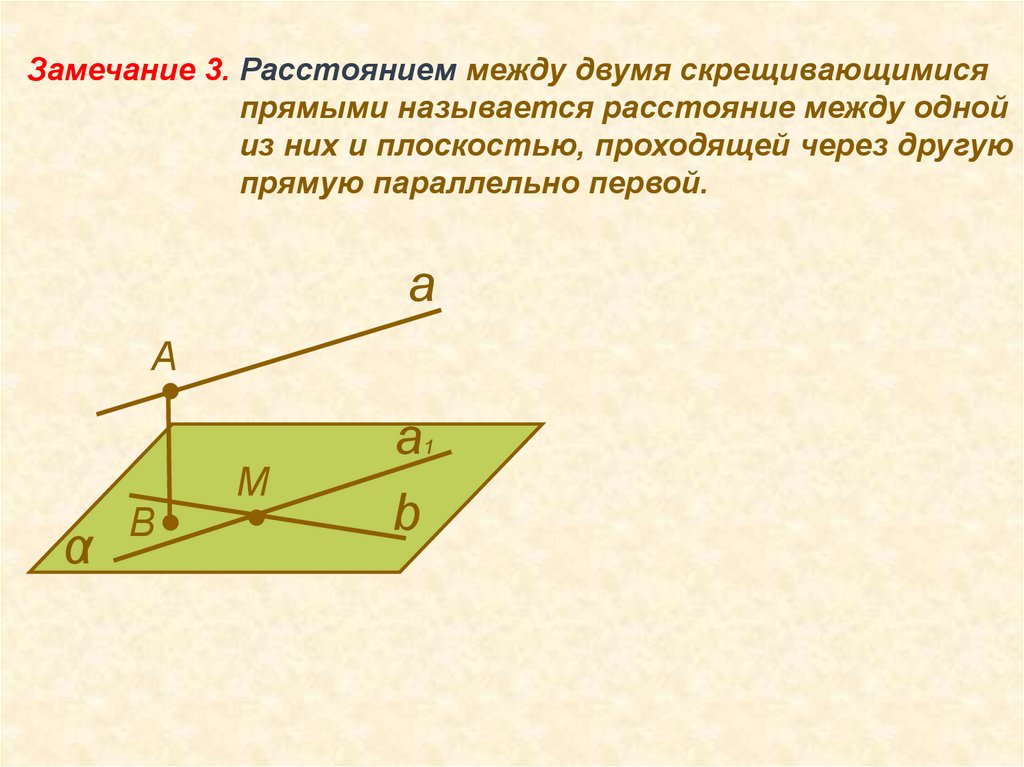
Замечание 3. Расстоянием между двумя скрещивающимися
прямыми называется расстояние между одной
из них и плоскостью, проходящей через другую
прямую параллельно первой.
а
A
M
α
B
а
b
1

6.

7. Теорема о трех перпендикулярах

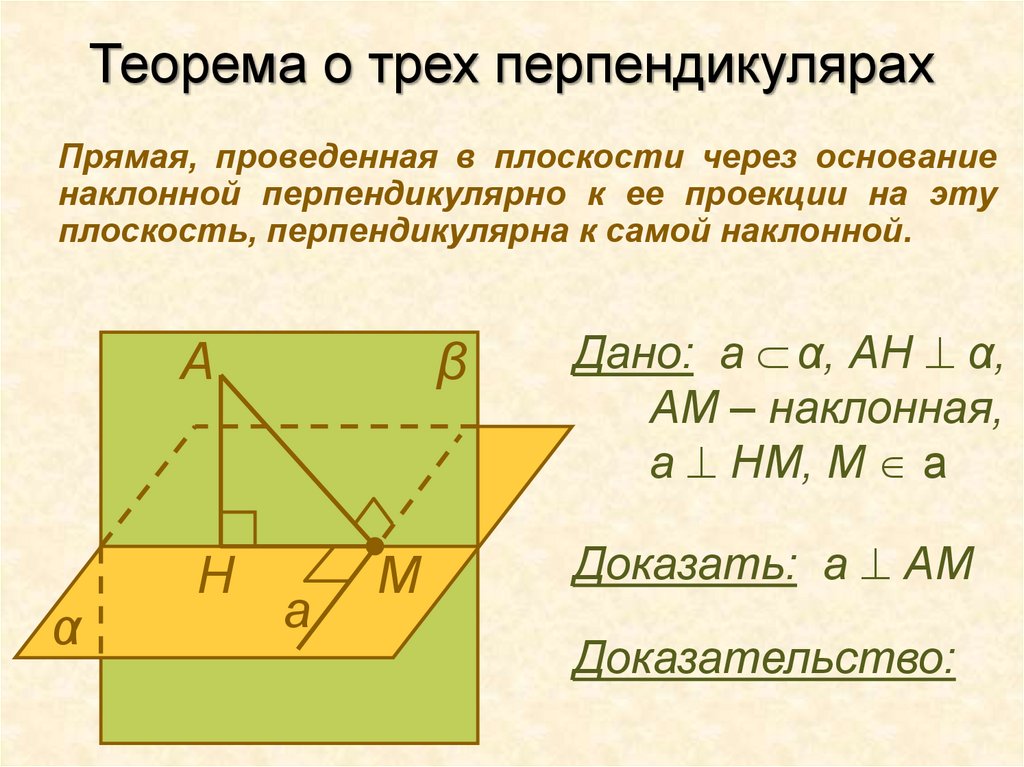
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна к самой наклонной.
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а НМ, М а
Доказать: а АМ
Доказательство:

8.

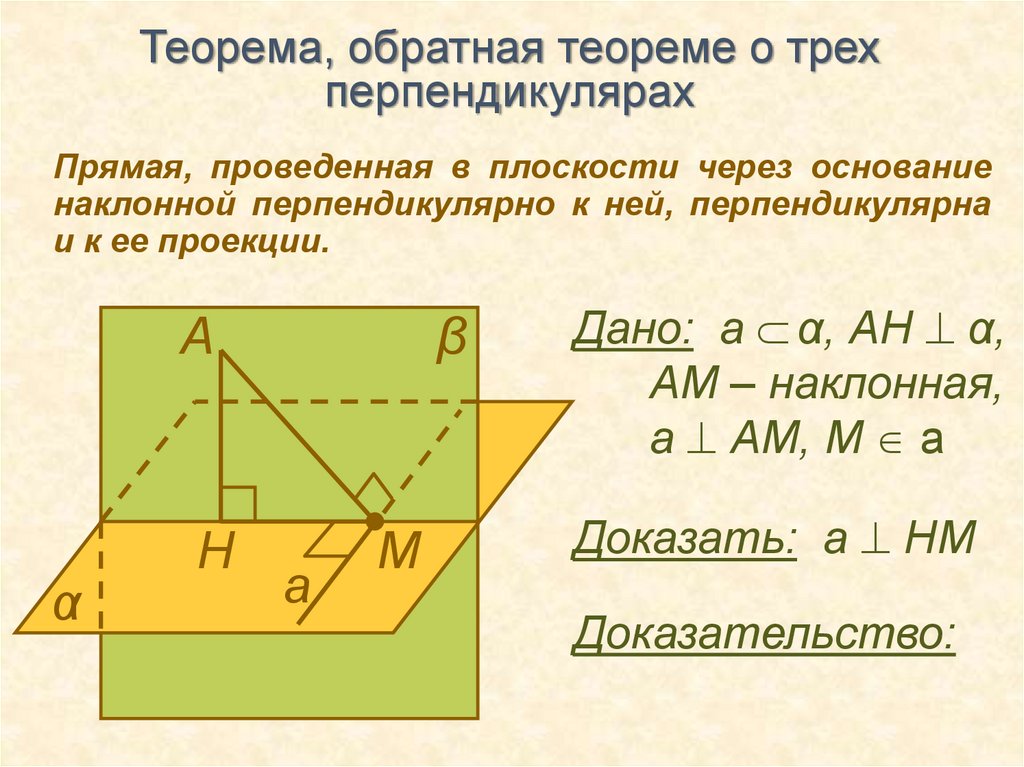
Теорема, обратная теореме о трех
перпендикулярах
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней, перпендикулярна
и к ее проекции.
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а АМ, М а
Доказать: а НМ
Доказательство:

9.

10.

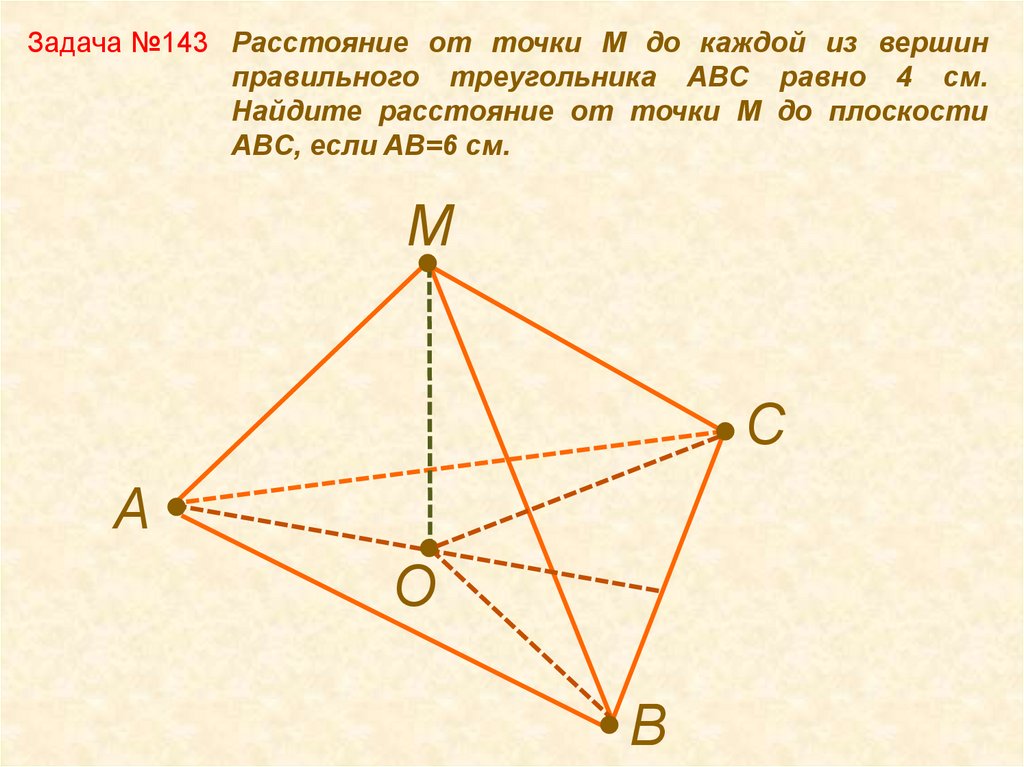
Задача №143 Расстояние от точки M до каждой из вершин
правильного треугольника ABC равно 4 см.
Найдите расстояние от точки M до плоскости
ABC, если AB=6 см.
М
C
А
O
В

11.

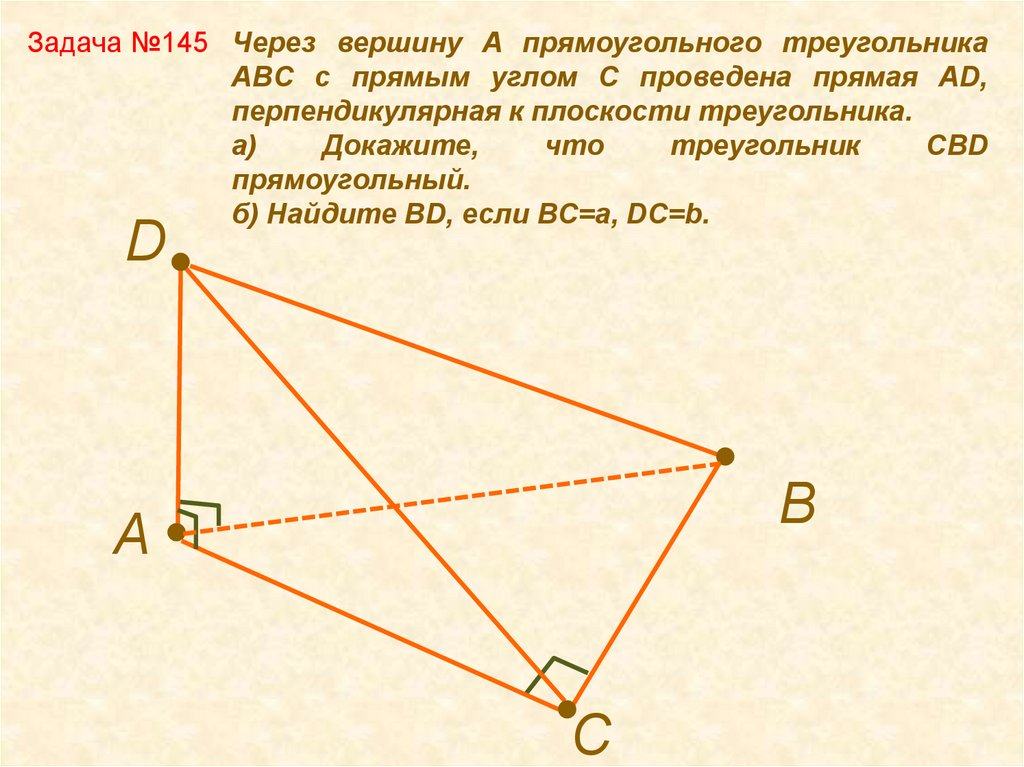
Задача №145 Через вершину A прямоугольного треугольника
ABC с прямым углом C проведена прямая AD,
перпендикулярная к плоскости треугольника.
а)
Докажите,
что
треугольник
CBD
прямоугольный.
б) Найдите BD, если BC=a, DC=b.
D
В
А
C

12.

Домашнее задание
§2 п.19-20, стр.40-42, теоремы
№ 139, 140, 141
Дополнительно:
№ 142, 153