Геометрические характеристики сечений. Основные понятия

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Тема 5
Геометрические характеристики сечений
Основные понятия
Геометрические характеристики простейших фигур
Моменты инерции при параллельном переносе осей
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
1

2.

Тема 3. Геометрические характеристики сечений
3.1. Основные понятия
1. Площадь поперечного сечения (м2, см2, мм2).
(5.1)
2. Статический момент сечения (м3, см3, мм3).
(5.2)
2

3.

(5.3)
Координаты центра тяжести:
(5.4)
3. Осевой (экваториальный) момент инерции (м4, см4, мм4).
(5.5)
3

4.

Для составного сечения:
I z I iz ; I y I iy .
(5.6)
4. Полярный момент инерции (м4, см4, мм4).
(5.7)
I p Iz I y .
2 y2 z2 ,
5. Центробежный момент инерции (м4, см4, мм4).
(5.8)
6. Полярный момент сопротивления (м3, см3, мм3).
Wp
Ip
max
.
(5.9)
4

5.

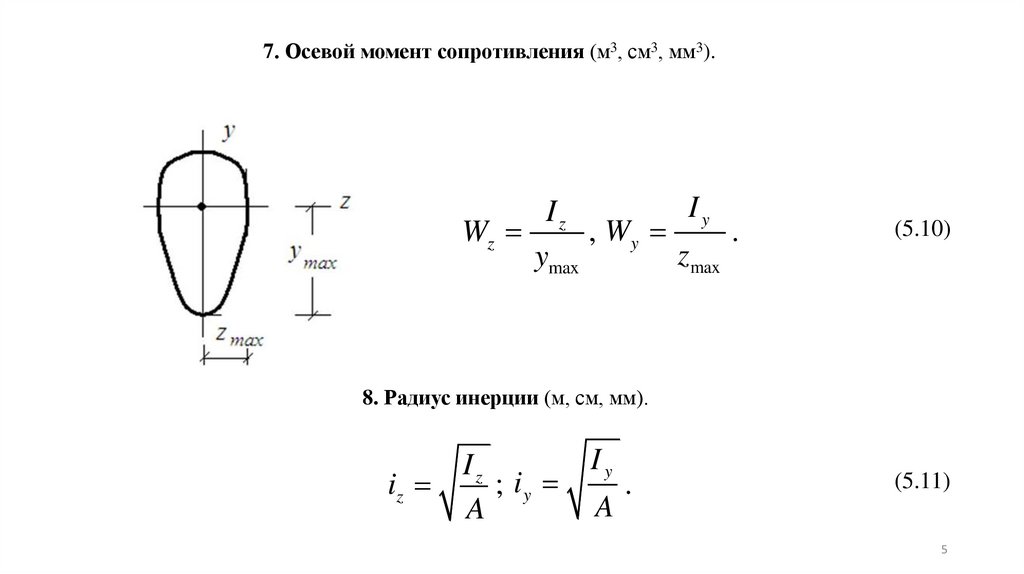
7. Осевой момент сопротивления (м3, см3, мм3).
Iy
Iz
Wz
, Wy
.
zmax
ymax
(5.10)
8. Радиус инерции (м, см, мм).
iz
Iz
; iy
A
Iy
A
.
(5.11)
5

6.

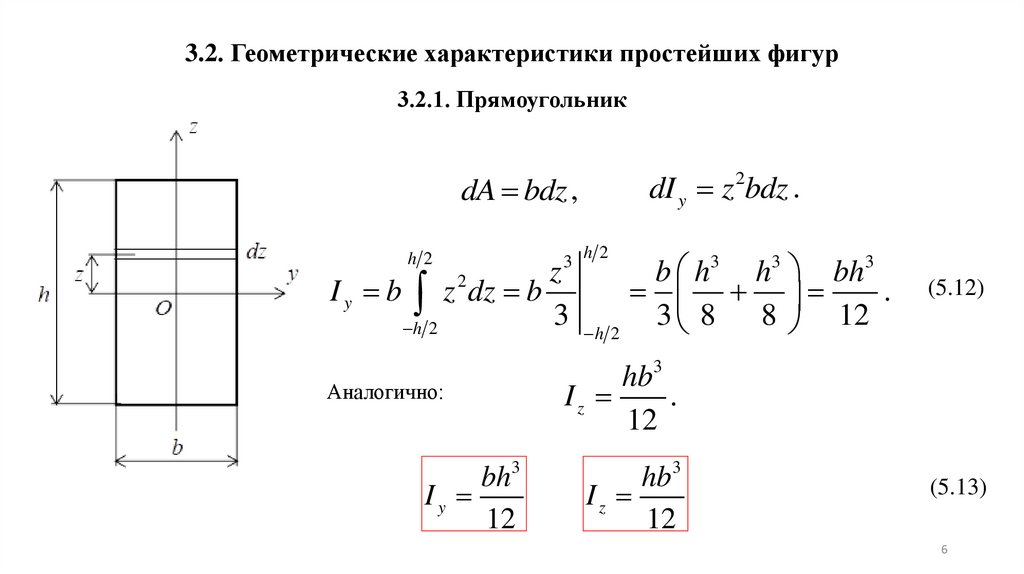
3.2. Геометрические характеристики простейших фигур
3.2.1. Прямоугольник
dI y z 2bdz .
dA bdz ,
h2
3
3
3
z
b h h
bh
2
I y b z dz b
.
3 h 2 3 8 8 12
h 2
h2
Аналогично:
bh3
Iy
12
3
(5.12)
hb3
Iz
.
12
hb3
Iz
12
(5.13)
6

7.

Радиусы инерции:
iy
bh3
h
h
;
A
12 bh
12 3,464
Iy
(5.14)
iz
Iz
hb3
b
b
.
A
12 bh
12 3,464
Моменты сопротивления:
bh 2 bh
Wy
;
zmax h 2 12 h
6
Iy
Iy
3
bh 2
Wy
6
2
Iz
Iz
hb3 2 hb 2
Wz
.
ymax b 2 12 b
6
hb 2
Wz
6
(5.15)
7

8.

3.2.2. Круг
dI p 2 d d 3d d .
R
2
0
0
I p 3 d d
Ip
R4
2
(5.16)
4 R
4 0
2
0
I y Iz
R 4 2 R 4
.
4
2
R4
(5.17)
4
8

9.

Выражения через диаметр круга:
Ip
d 2
4
2
d
4
32
; I y Iz
d 2
4
4
d4
64
.
(5.18)
Радиус инерции:
iy iz
R4
R d
.
2
A
4 R
2 4
Iy
(5.19)
Моменты сопротивления:
Wp
Ip
R
R3
2
d3
16
; Wy Wz
R3
4
d3
32
.
(5.20)
9

10.

3.2.3. Кольцо
Ip
D4
32
I y Iz
D4
64
d4
32
d4
64
32
4
4
D
d
64
D4
32
4
4
D
d
4
1
.
D4
64
4
1
.
(5.21)
(5.22)
Через радиус:
R4
4
1
.
(5.23)
R
2
i y iz
1
.
2
2
4 R 1 2
(5.24)
Ip
2
4
1
; I y Iz
R4
4
Радиусы инерции:
R 4 1 4
10

11.

Моменты сопротивления:
Wp
R3
2
Wy Wz
4
1
R3
4
D3
16
4
1
4
1
;
D3
32
4
1
.
(5.25)
(5.26)
11

12.

3.2.4. Прямоугольный треугольник
z
b z b 1 .
h
z
dA b z dz b 1 dz .
h
z
dI y z dA bz 1 dz .
h
2
2
3 h
4 h
b 3
bz
bz
z
2
I y z dA bz 1 dz b z dz z dz
h0
3 0 h 4 0
h
A
0
0
3
3
3
3
hb
bh bh
bh
(5.27)
Iz
.
.
12
3
4
12
12
h
2
h
2
h

13.

h
2 b 1 z h
y z
y
dz
I yz yzdA yzdydz z ydy dz z
0
2 0
A
0 0
0
0
h y z
h
h
b
b
z
z
b z
2z
z
z
z 1 dz z 2 2 dz
2
2 0 h
2 0
h h
2 2 3h 4h 0
2 h
2
2 h
2
3
b 2 h 2 2h 2 h 2 b 2 h 2 b 2 h 2
.
2 2
3
4 2 12
24
2
2
3
4
(5.28)
13

14.

3.3. Моменты инерции при параллельном переносе осей
I y1 z dA z b dA z 2 dA 2b zdA b 2 dA .
2
2
1
A
2
z
dA I y .
A
A
A
A
A
dA A .
A
14

15.

I z1 I z a 2 A .
I y1 I y b2 A .
(5.27)
Центробежный момент инерции:
I y1z1 y1 z1dA y a z b dA yz az by ab dA
A
A
A
yzda a zdA b ydA ab dA .
A
A
A
A
yzdA I . zdA S 0. ydA S 0. dA A.
y
yz
A
I y1z1 I yz abA.
A
z
A
A
(5.28)
15

16.

Теорема Штайнера-Гюйгенса
I y1 I y b 2 A.
I z1 I z a 2 A.
(5.29)
I y1z1 I yz abA.
b2h2
bh3
hb3
I y1
; I z1
; I y1 z1
.
12
12
24
2
3
3
3
3
bh
h
bh
bh
bh
bh
.
I y I y1 b 2 A
12 3 2
12 18
36
2
(5.30)
3
3
3
hb
b
bh
hb
hb
hb
.
I z I z1 a 2 A
12 3 2
12 18
36
3
16

17.

b 2 h 2 b h bh b 2 h 2 b 2 h 2
b2h2
I yz I y1z1 abA
.
24 3 3 2
24
18
72
(5.31)
Правило для определения знака центробежного момента инерции треугольника:
Если гипотенуза треугольника в принятой системе осей следует вдоль
графика убывающей линейной функции, то центробежный момент
инерции отрицателен, и наоборот.
17

18.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
[email protected]
18