Похожие презентации:
Тепломассообмен в энергетическом оборудовании. Краткий конспект лекций
1.
ТЕПЛОМАССООБМЕН В ЭНЕРГЕТИЧЕСКОМОБОРУДОВАНИИ
КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ
к.т.н. Клушин Е.А.
klushin_ea@mail.ru
Список литературы
1. Исаченко В.П., Осипова В.А. Сукомел А.С. Теплопередача : Учеб.для
вузов, 2014. -М.:Арис, - 416 с.,ил.
2. Цветков Ф.Ф., Григорьев Б.А. Тепломассобмен : Учеб. пособие для вузов,
2006. -М.: Издательский дом МЭИ, - 550 с.,ил.
3. Кириллов П.Л., Богословская Г.П. Тепломассобмен в ядерных
энергетических установках: Учеб. Пособие для вузов, 2008 г. –М: ИздАт.,
-256 с.
4. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчётам (ядерные реактор, теплообменники,
парогенераторы) – М.: Энергоатомиздат, 1990. - 359с.
2.
Содержание1. ВВЕДЕНИЕ
2. ТЕМПЕРАТУРНОЕ ПОЛЕ. ТЕМПЕРАТУРНЫЙ ГРАДИЕНТ.
3. ЗАКОН ФУРЬЕ
4. КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИ
5. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
6. УСЛОВИЯ ОДНОЗНАЧНОСТИ ДЛЯ ПРОЦЕССОВ ТЕПЛОПРОВОДНОСТИ
7. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
8. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
9. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПРОВОДНОСТИ
3.
ВведениеВместе с термодинамикой теория теплообмена является теоретическим фундаментом
теплотехники.
Теория теплообмена позволяет определять интенсивность и скорость переноса тепла.
Если в среде возникла разность температур, то энергия переносится из области
высокой температуры в область низкой. Такой процесс называется теплообменом
(теплопередачей).
Этим термином объединяются три различных процесса, результатом которых является
перенос тепла из одной части пространства в другую:
теплопроводность - перенос тепла посредством передачи энергии теплового
движения частиц в среде;
конвекция — перенос тепла при перемещении макроскопических элементов среды;
тепловое излучение — распространение энергии электромагнитными волнами.
Теплообмен это самопроизвольный процесс и как любой реальный самопроизвольный
процесс является необратимым.
Основными понятиями теории теплообмена являются: температурное поле,
температурный градиент, тепловой поток.
Явление теплопроводности представляет собой процесс распространения тепловой
энергии при непосредственном соприкосновении отдельных частиц тела или отдельных
тел, имеющих различные температуры. Теплопроводность обусловлена движением
микрочастиц вещества.
4.
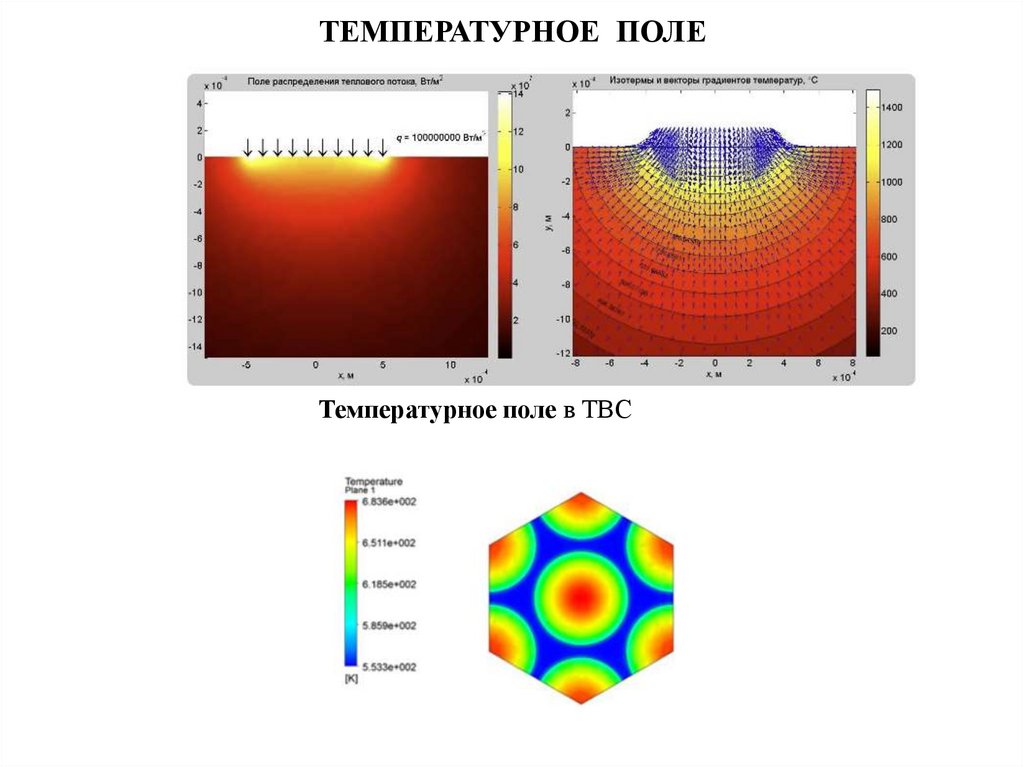
ТЕМПЕРАТУРНОЕ ПОЛЕТемпературное поле это совокупность значений температуры во всех точках
изучаемого пространства для каждого момента времени.
Аналитическое исследование теплопроводности сводится к изучению
пространственно-временного изменения температуры, т. е. к нахождению
уравнения:
t=f(x, у, z, τ).
Это уравнение представляет математическое выражение температурного
поля. Температурное поле можно рассматривать в пространстве как
одномерном, так и в 2-х и 3-х мерном прближении.
Различают стационарное и нестационарное температурные поля.
Пример: распределение температуры твэла и теплоносителя.
5.
ТЕМПЕРАТУРНОЕ ПОЛЕТемпературное поле в ТВС
6.
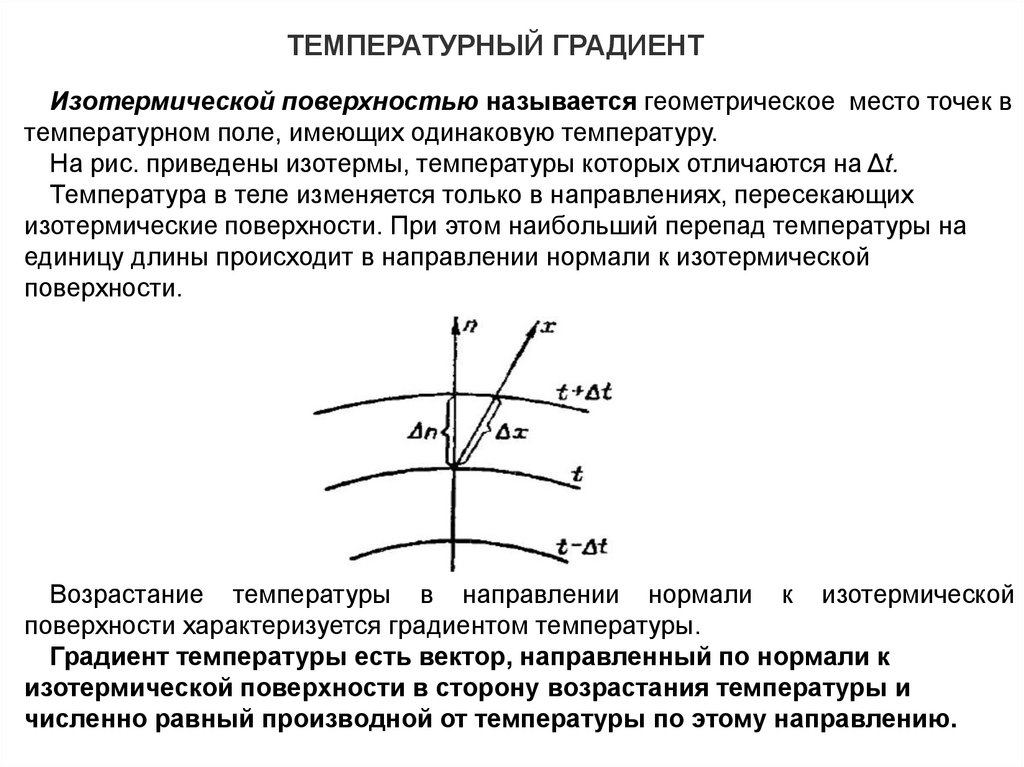
ТЕМПЕРАТУРНЫЙ ГРАДИЕНТИзотермической поверхностью называется геометрическое место точек в
температурном поле, имеющих одинаковую температуру.
На рис. приведены изотермы, температуры которых отличаются на Δt.
Температура в теле изменяется только в направлениях, пересекающих
изотермические поверхности. При этом наибольший перепад температуры на
единицу длины происходит в направлении нормали к изотермической
поверхности.
Возрастание температуры в направлении нормали к изотермической
поверхности характеризуется градиентом температуры.
Градиент температуры есть вектор, направленный по нормали к
изотермической поверхности в сторону возрастания температуры и
численно равный производной от температуры по этому направлению.
7.
ЗАКОН ФУРЬЕПлотностью теплового потока называется количество теплоты, проходящее
в единицу времени через единицу площади изотермической поверхности
q = Вт/м2.
В 1807 году французский ученый Жан-Батист Фурье доказал
экспериментально, что имеется однозначная линейная взаимосвязь
между тепловым потоком и градиентом температуры.
В соответствии с законом Фурье (основным законом теплопроводности)
плотность теплового потока равна:
где: λ - коэффициент теплопроводности (Вт/м*К), равный количеству тепла,
которая проходит в единицу времени через единицу поверхности, при разности
температур в 1К на толщине 1м;
n0 — единичный вектор, нормальный к изотермической поверхности и
направленный в сторону возрастания температуры;
δt/δn — производная температуры по нормали n.
Знак минус отражает очевидный факт, что тепловой поток направлен в сторону
уменьшения температуры.
Для определения количества тепла проходящего через плоскую стенку можно
использовать формулу в интегральном виде:
Q = (tc1- tc2) λ F / δ
8.
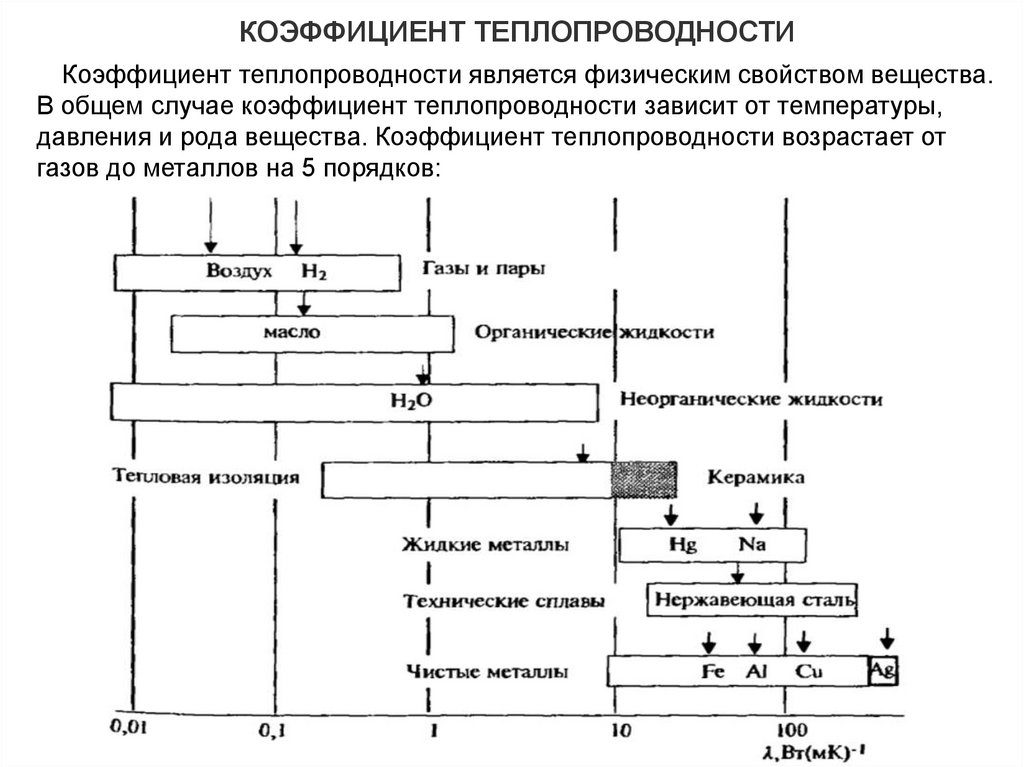
КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИКоэффициент теплопроводности является физическим свойством вещества.
В общем случае коэффициент теплопроводности зависит от температуры,
давления и рода вещества. Коэффициент теплопроводности возрастает от
газов до металлов на 5 порядков:
9.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИДля решения задач, связанных с нахождением температурного поля,
универсальным инструментом является дифференциальное уравнение
теплопроводности.
В основу вывода диф. уравнения теплопроводности положен закон сохранения
энергии, который в рассматриваемом случае может быть сформулирован
следующим образом: количество теплоты, введенное в элементарный объем
извне за время dτ вследствие теплопроводности, а также от внутренних
источников, равно изменению внутренней энергии вещества содержащегося в
элементарном объеме:
dQ1+dQ2=dQ,
где dQ1 — количество теплоты, Дж, введенное в элементарный объем путем
теплопроводности за время d τ;
dQ2—количество теплоты, которое за время d τ выделилось в элементарном
объеме dv за счет внутренних источников;
dQ — изменение внутренней энергии, содержащейся в элементарном объеме
dv, за время dτ.
10.
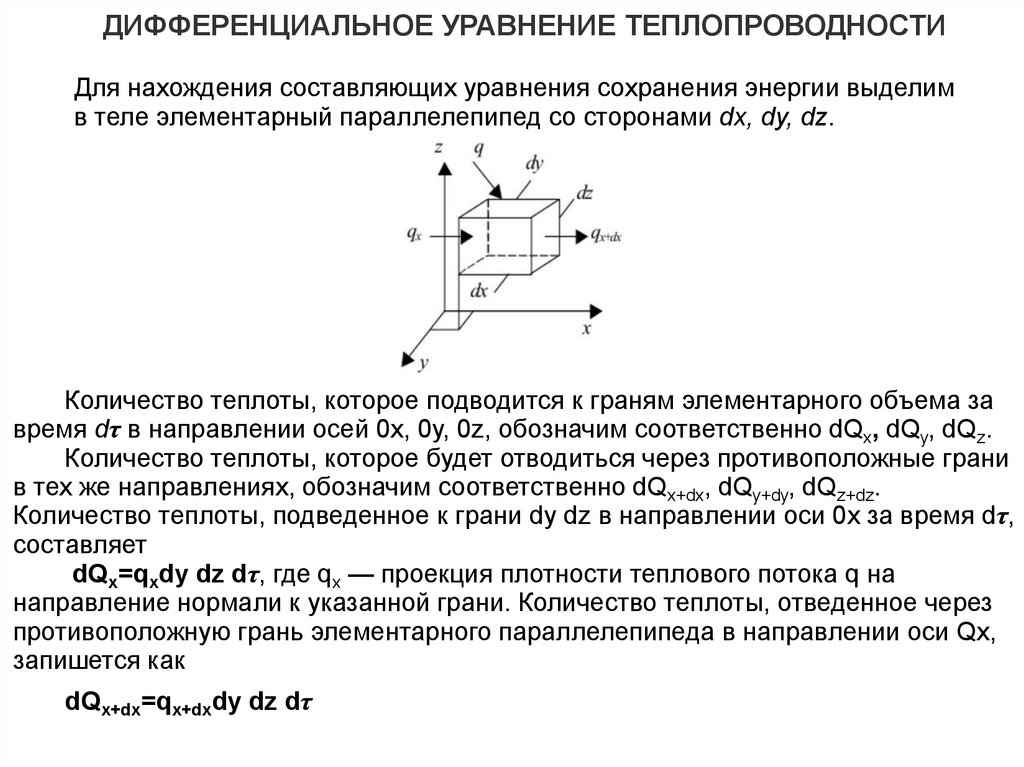
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИДля нахождения составляющих уравнения сохранения энергии выделим
в теле элементарный параллелепипед со сторонами dx, dy, dz.
Количество теплоты, которое подводится к граням элементарного объема за
время dτ в направлении осей 0x, 0у, 0z, обозначим соответственно dQx, dQy, dQz.
Количество теплоты, которое будет отводиться через противоположные грани
в тех же направлениях, обозначим соответственно dQx+dx, dQy+dy, dQz+dz.
Количество теплоты, подведенное к грани dy dz в направлении оси 0х за время dτ,
составляет
dQx=qxdy dz dτ, где qx — проекция плотности теплового потока q на
направление нормали к указанной грани. Количество теплоты, отведенное через
противоположную грань элементарного параллелепипеда в направлении оси Qх,
запишется как
dQx+dx=qx+dxdy dz dτ
11.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИРазница количеств теплоты, подведенного к элементарному параллелепипеду и
отведенного от него за время dτ в направлении оси Qx , представляет собой
количество теплоты:
dQx1=qxdy dz dτ - qx+dxdy dz dτ
Функция qx+dx является непрерывной в рассматриваемом интервале dx и может
быть разложена в ряд Тейлора:
Если ограничиться двумя первыми членами ряда, то уравнение для количества
теплоты, подводимого к элементарному объему в направлении оси 0x запишется
в виде:
dQx1 = - (δqx/δx) dx dy dz dτ
Аналогичным образом можно найти количество теплоты, подводимое к
элементарному объему и в направлениях двух других координатных осей Qу и Qz.
Количество теплоты dQ1, подведенное теплопроводностью к рассматриваемому
объему, будет равно:
12.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИВторая составляющая уравнения сохранения энергии является теплотой,
выделяемой внутренними источниками:
dQ2=qvdv dτ
Третья составляющая уравнения сохранения энергии зависит от характера
термодинамического процесса. В изохорическом процессе вся теплота уходит
на изменение внутренней энергии (dQ= dU). Из термодинамики известно:
Подставляя полученные выражения в уравнение сохранения энергии, получим
дифференциальное уравнение изохорического процесса переноса теплоты (в
частности для твёрдых тел):
или используя принятые в математике обозначения:
13.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИС учётом того, что в твёрдых телах перенос теплоты осуществляется по
закону Фурье, можно записать:
Поскольку принято, что теплофизические свойства постоянные, то уравнение
принимает вид:
Обозначим:
и
тогда, в общем виде дифференциальное уравнение теплопроводности
запишется так:
а=λ/сρ, м2/с, называется коэффициентом температуропроводности,
который характеризует скорость изменения температуры.
14.
УСЛОВИЯ ОДНОЗНАЧНОСТИ ДЛЯ ПРОЦЕССОВТЕПЛОПРОВОДНОСТИ
Дифференциальное уравнение теплопроводности описывает целый класс
явлений теплопроводности. Чтобы выделить конкретный процесс и дать его
полное математическое описание, к диф. уравнению необходимо присоединить
математическое описание всех особенностей рассматриваемого процесса,
которые называются условиями однозначности или краевыми условиями.
Условия однозначности включают в себя:
геометрические условия, характеризующие форму и размеры тел, в которых
протекает процесс;
физические условия, характеризующие физические свойства среды и тела;
начальные условия, характеризующие распределение температур в
изучаемом теле в начальный момент времени;
граничные условия, характеризующие взаимодействие рассматриваемого
тела с окружающей средой.
Граничные условия могут быть заданы несколькими способами:
а) Граничные условия первого рода. При этом задается распределение
температуры на поверхности тела для каждого момента времени:
б) Граничные условия второго рода. При этом задаются значения теплового
потока для каждой точки поверхности тела и любого момента времени.
в) Граничные условия третьего рода. При этом задаются температура
окружающей среды tж и закон теплообмена между поверхностью тела и
окружающей средой.
15.
Граничные условия третьего родаГраничные условия третьего рода требуют знание закона теплообмена между
поверхностью и окружающей средой в процессе охлаждения и нагревания тела.
Процесс теплообмена между поверхностью тела и средой относится к очень
сложным процессам и зависит от большого количества параметров. Далее эти
вопросы будут подробно рассмотрены.
Для описания процесса теплообмена между поверхностью тела и средой
используется закон Ньютона—Рихмана согласно которому количество теплоты,
отдаваемое единицей поверхности тела в единицу времени, пропорционально
разности температур поверхности тела tс и окружающей среды tж
q=α(tc— tж),
где α — коэффициент пропорциональности, называемый коэффициентом
теплоотдачи, Вт/(м2К).
Коэффициент теплоотдачи характеризует интенсивность теплообмена между
поверхностью тела и окружающей средой. Численно он равен количеству
теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу
времени при разности температур между поверхностью тела и окружающей
средой, равной одному градусу.
Определение коэффициента теплоотдачи является наиболее сложной и
важной задачей теории теплообмена.
16.
ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕПри установившемся, или стационарном, тепловом режиме температура тела во
времени остается постоянной:
Рассмотрим теплопроводность в телах простейшей геометрической формы при
отсутствии внутренних тепловыделений.
Граничные условия первого рода
Рассмотрим однородную и изотропную стенку толщиной δ с постоянным
коэффициентом теплопроводности λ. На наружных поверхностях
стенки поддерживают постоянными температуры tc1 и tC2.
При заданных условиях температура будет изменяться только
в направлении, перпендикулярном плоскости стенки. Если ось Ох
направить, как показано на рис., то температура в направлении
осей 0у и 0z будет оставаться постоянной поэтому:
Граничные условия в рассматриваемой задаче зададим
следующим образом:
при х=0 t = tc1 ,
при х=δ t = tc2 .
В результате двойного интегрирования получим: t=C1 х + C2.
Постоянные C1 и C2 определяются из граничных условий:
при х=0 t = tc1 и C2=tc1
при х=δ t = tc2 и C1= - (tc1- tc2)/δ.
Итак получен линейный закон распределения температуры в рассматриваемой плоской
стенке:
t = tc1 - x(tc1- tc2)/δ. При этом q = (tc1- tc2) λ/δ.
17.
Граничные условия третьего родаЭто наиболее важная и часто встречающаяся на практике задача.
Передача тепла из одной подвижной среды (жидкости или газа) к другой через
разделяющую их однородную или многослойную твердую стенку любой формы
называется теплопередачей.
Рассмотрим теплопередачу через однородную и многослойную плоскую стенку. Пусть
плоская однородная стенка имеет толщину δ. Заданы коэффициенты теплопроводности
стенки λ температуры окружающей среды tж1 и tж2, а также коэффициенты теплоотдачи α1
и α2; будем считать, что величины tж1 , tж2 , α1 и α2 постоянны.
Решение задачи при этих условиях даёт уравнение
для плотности теплового потока:
где
Величина k имеет ту же размерность, что и α , Вт/(м2К), и
называется коэффициентом теплопередачи.
Величина, обратная коэффициенту теплопередачи (знаменатель формулы для k),
называется полным термическим сопротивлением теплопередачи.
Подобные аналитические решения получены для тел различных конфигураций и
граничных условий, включая стенки с внутренним тепловыделением, а также для
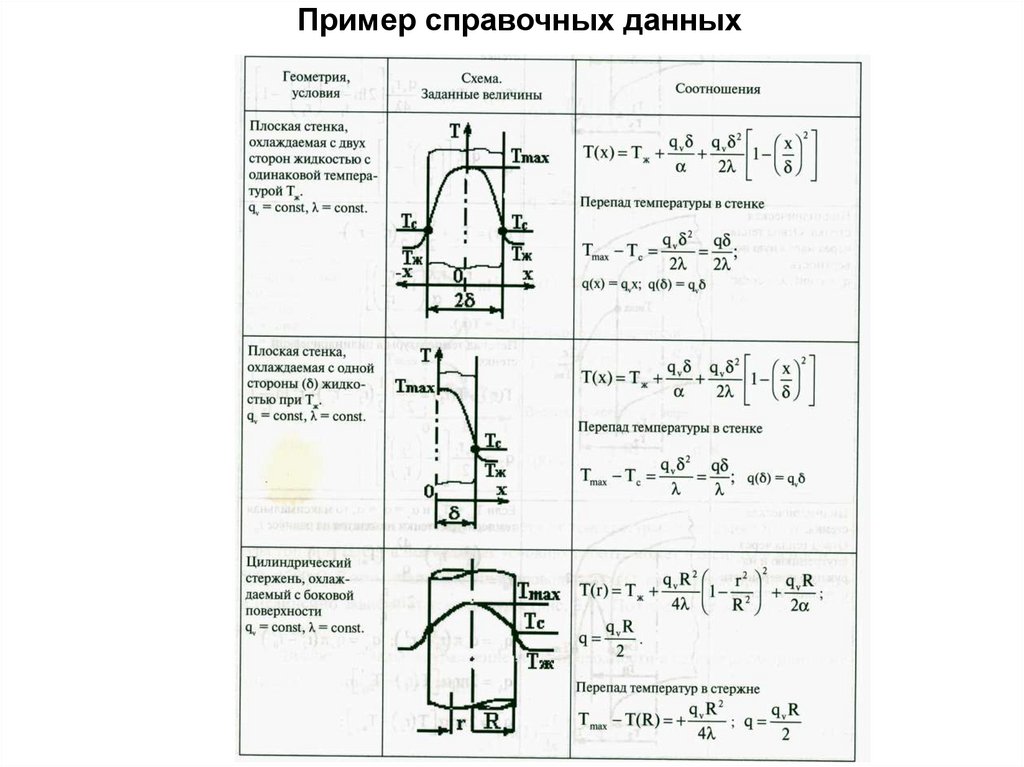
оребрённых поверхностей. Результаты содержатся в справочниках.
18.
Пример справочных данных19.
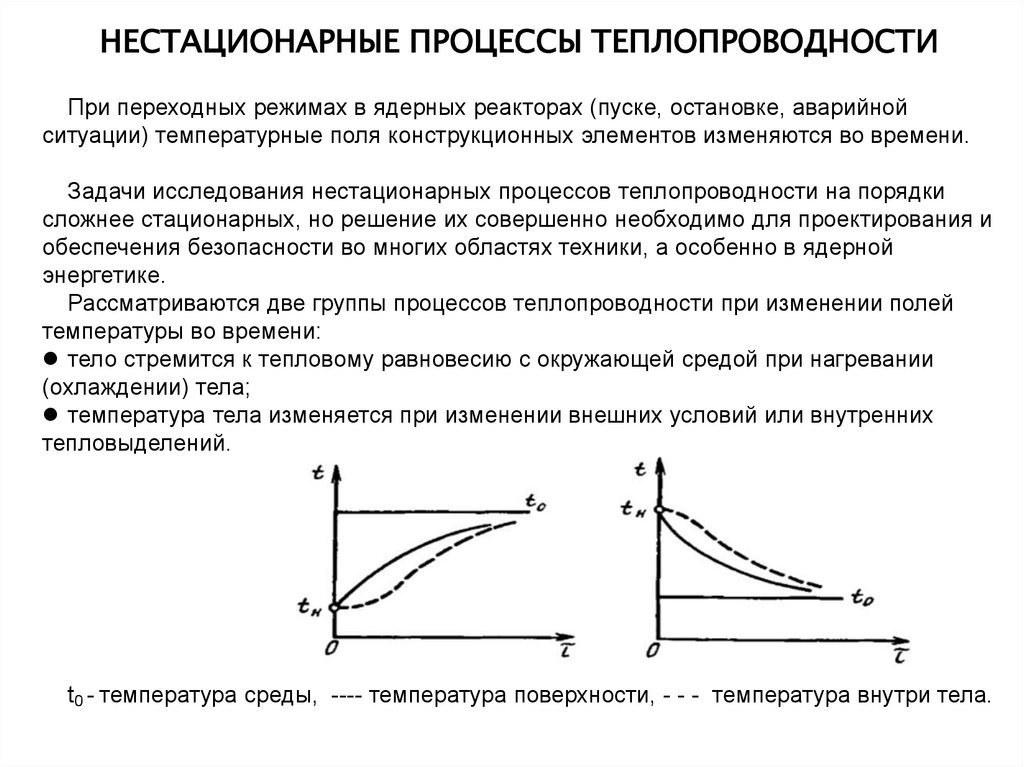
НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПРОВОДНОСТИПри переходных режимах в ядерных реакторах (пуске, остановке, аварийной
ситуации) температурные поля конструкционных элементов изменяются во времени.
Задачи исследования нестационарных процессов теплопроводности на порядки
сложнее стационарных, но решение их совершенно необходимо для проектирования и
обеспечения безопасности во многих областях техники, а особенно в ядерной
энергетике.
Рассматриваются две группы процессов теплопроводности при изменении полей
температуры во времени:
тело стремится к тепловому равновесию с окружающей средой при нагревании
(охлаждении) тела;
температура тела изменяется при изменении внешних условий или внутренних
тепловыделений.
t0 - температура среды, ---- температура поверхности, - - - температура внутри тела.
20.
НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПРОВОДНОСТИДля примера рассмотрим простейший случай передачи теплоты через стенку при
внезапном изменении температуры одного из теплоносителей. В нестационарных
процессах теплопроводности не вся теплота передаётся через стенку: часть ее уйдет на
изменение внутренней энергии самой стенки (ее температуры), и только при наступлении
стационарного процесса вся теплота будет передаваться через стенку от одной жидкости к
другой. Нестационарные тепловые процессы всегда связаны с изменением внутренней
энергии или энтальпии вещества.
Дифференциальное одномерное уравнение нестационарной теплопроводности имеет
вид:
Здесь:
;
- температура окружающей среды;
- коэффициент температуропроводности;
Температура тела изменяется во времени, но одинакова во всех точках тела, т.е.
внутреннее термическое сопротивление тела пренебрежимо мало. Обозначим t - t0=ϑ.
Решение уравнения имеет вид :
Это простейший случай. Реальные задачи сложны и аналитическое решение во многих
случаях получить практически невозможно, поэтому при решении задач нестационарной
теплопроводности часто используются численные методы.
21.
Численное решение задач теплопроводностиАналитическое решение задач теплопроводности возможно лишь для тел простой
геометрической формы и при простейших граничных условиях.
На практике же возникает необходимость определить температурное поле в телах
более сложной формы или при таких условиях однозначности, когда температура или
условия теплообмена на поверхности тела непостоянны, когда величина λ существенно и
нелинейно зависит от температуры, когда тело неоднородно и величина λ различна в
разных точках тела и по разным направлениям. Такие задачи можно решать только
численными методами при этом непрерывный процесс теплопроводности заменяется
дискретным процессом.
Исследуемое тело мысленно разделяют на небольшие объемы простой формы, в
результате образуется пространственная сетка. При этом считают, что в пределах
каждого такого объема свойства вещества, мощность внутренних источников и
температура остаются постоянными.
Центральные точки выделенных объемов (узлов) образуют внутри тела
пространственную сетку. Для любого узла такой сетки путем замены дифференциального
уравнения теплопроводности его конечно - разностным аналогом (от бесконечно малых
приращений переходят к малым конечным приращениям) можно получить
алгебраические соотношения, составляющие замкнутую систему уравнений, для
решения которой используются численные методы. Этот подход называют методом
конечных разностей.
22.
Численное решение задач теплопроводностиНапример, в выражении производной δt2/δх2 заменим бесконечно малые приращения
dt и dx малыми конечными величинами Δt и Δх для точки с координатой m:
Для определения производных по оси х рассмотрим трёхточечную схему:
dt tm 1 tm
dx
x
d 2t (tm 1 tm ) (tm tm 1 )
2
dx
x 2
23.
Численное решение уравнения теплопроводностиВ результате получаем нелинейную систему алгебраических уравнений, которая
решается каким-либо численным методом. Но это тоже очень непростая задача. Система
уравнений чаще всего бывает существенно нелинейной и огромной размерности. При
решении возникает много проблем, среди которых основные проблемы устойчивости и
сходимости.
Однако, в конечном счёте, удаётся получить решение с необходимой точностью
практически для любой задачи.
С развитием вычислительных возможностей компьютеров и математических методов
численные методы стали основными для решения сложных практических задач. Но это не
значит, что аналитические методы умерли. Для разных задач используются наиболее
подходящие методы, просто арсенал у инженеров и учёных вырос.

















 Физика
Физика








