Prezentatsia_po_matematike_po_teme_Chetnye_i_nechetnye_funktsii

1.

Четность и нечетность
функции
21.10.24

2.

Цель урока :
Формирование понятий « четность
нечетность функции»; исследование
функций на четность; определение по
графику четных и нечетных функций;
построение графиков функций, содержащих
модуль, используя при этом свойство
четности и нечетности функций.

3.

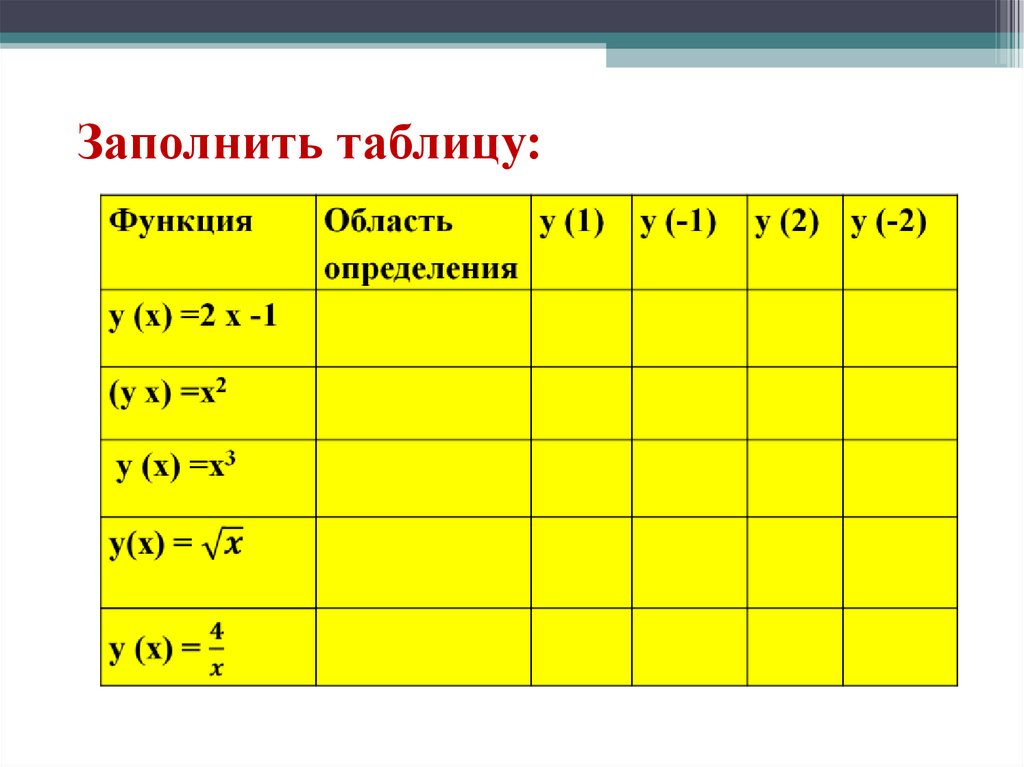
Заполнить таблицу:

4.

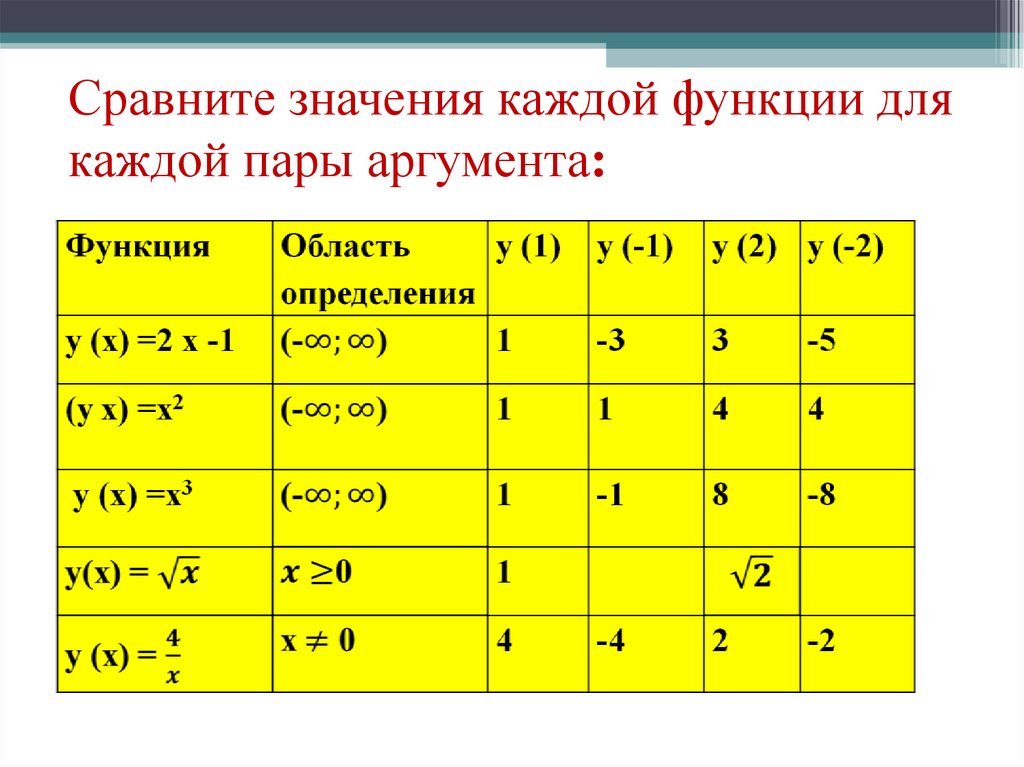
Сравните значения каждой функции для
каждой пары аргумента:

5.

3
а=1
Вершина(2;-4)
4

6.

1

7.

Понятие симметричности
Если числовое множество Х вместе с каждым
своим элементом х содержит и противоположный
элемент – х, то Х называют симметричным
множеством

8.

Определите симметричное множество
или нет:
1. (-6; 6),
2. [ -7; 7],
3. [0;+ ∞ ),
4. (-∞;+∞ ),
5. (-5; 3),
6. [-5; 5)
7. (-∞;-2),(2;+∞ )
8. (-∞;-8),[8;+∞ )

9.

Свойства функций
1) Область определения функций .
2) Монотонность функции.
3) Ограниченность функции .
4) Наибольшее и наименьшее значения
функции .
5) Непрерывность .
6) Область значений .
7) Выпуклость
8) Четность, нечетность.

10.

Запомнить:
Определение: Функция y(x) называется четной, если
область определения её симметрична относительно
начала координат и выполняется
y(-x) = y(x)
для любого x из области определения этой функции.
График четной функции симметричен относительно оси х.
Определение: Функция y(x) называется четной, если
область определения её симметрична относительно
начала координат и выполняется
y(-x) = - y(x)
График нечетной функции симметричен относительно начала
координат.

11.

Геометрический смысл свойств чётной и
нечётной функций.

12.

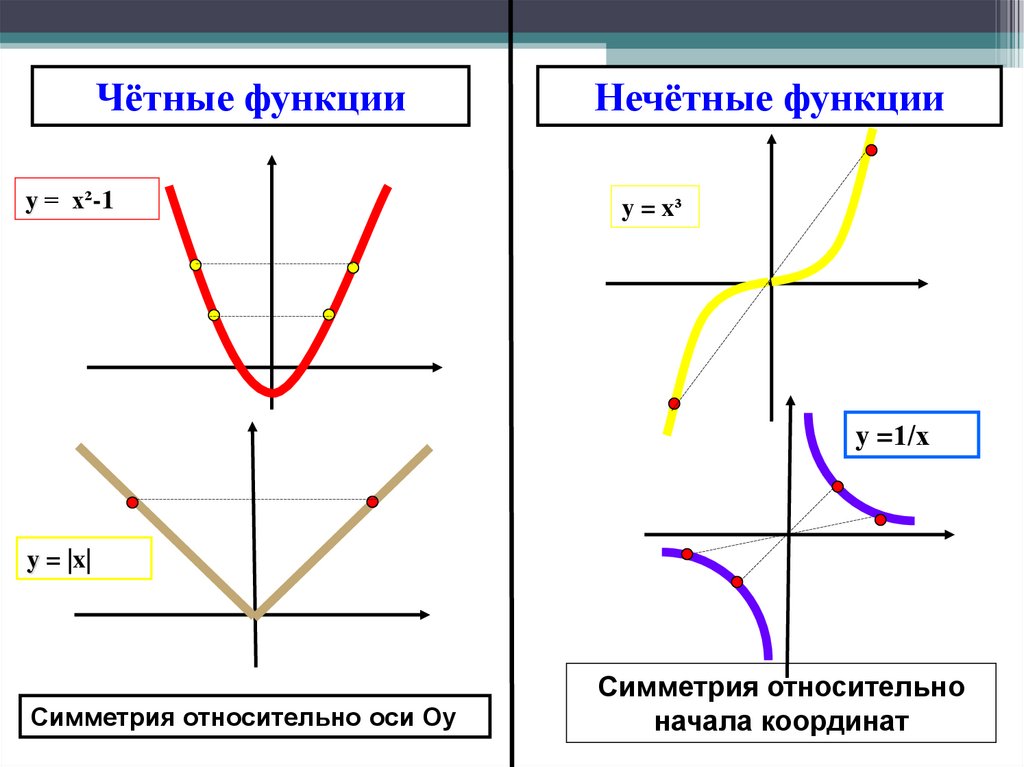
Чётные функции
y = x²-1
Нечётные функции
y = x³
y =1/х
y = |x|
Симметрия относительно оси Оy
Симметрия относительно
начала координат

13.

Алгоритм исследования функции на
чётность или нечетность
1)Установить , симметрична ли область
определения функции
2) Найти f(-x)
3) Сравнить f(-x) и f(x)

14.

Определение
Чётные функции
Нечётные функции
y (- x) = y (x)
y (- x) = - y (x)
Выяснить является ли функция чётной или нечётной.
y = 5 x²- |X|
Решение:
y (- x)=5 •(- x)² - |- x| =
= 5x² - |x|=
= y (x) - четная
y = 7x +x³
Решение:
y (- x)= 7(- x) +(- x)³=
= - 7 x - x³ =- (7x +x³)=
= - y (x)

15.

Примеры: Определите, является ли функция
четной или нечетной
1. f(x) =3 x2+x4
2. f(x) = х(5 – x2)
3 . f(x) =4 x6–x2
4.
f(x) = x7+2x3

16.

Чётные функции
Функция f(х) называется четной, если область её
определения симметрична относительно начала координат
и f(-x) = f(x) для любого х из области определения функции.
Графики чётных функций симметричны относительно оси
ординат.

17.

График четной функции симметричен
относительно оси ординат

18.

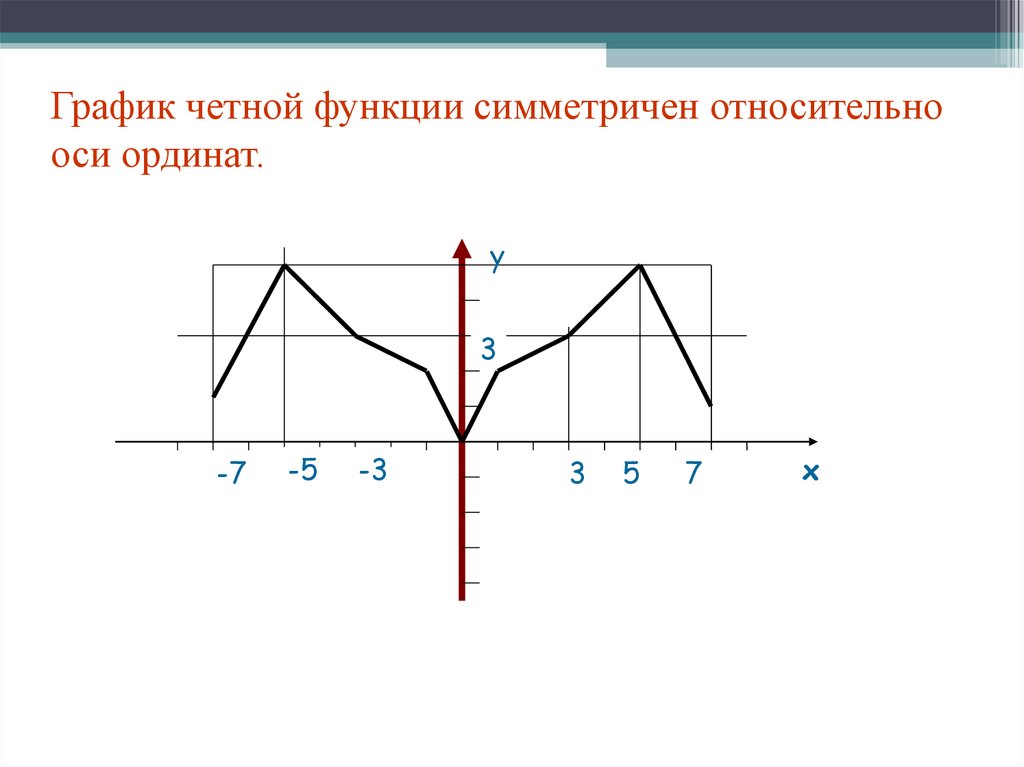
График четной функции симметричен относительно
оси ординат.
у
3
-7
-5
-3
3
5
7
х

19.

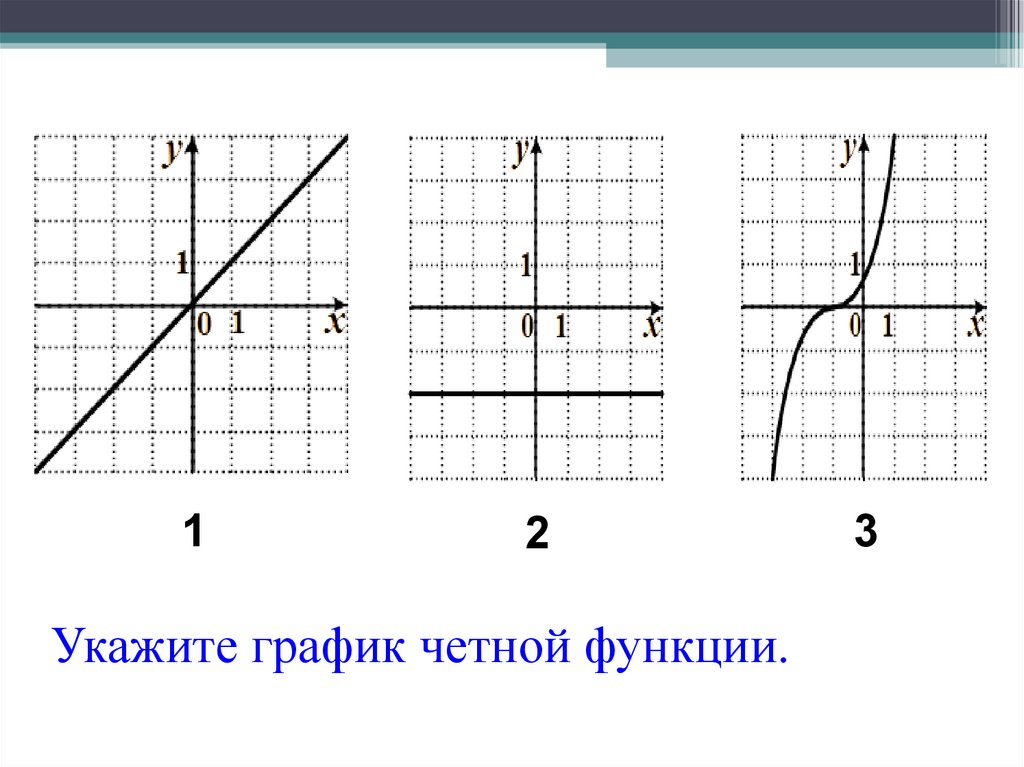
1
2
Укажите график четной функции.
3

20.

1
2
Укажите график четной функции.
3

21.

Нечётные функции
Функция f(х) называется нечетной, если область её
определения симметрична относительно начала координат
и f(-x) = -f(x) для любого х из области определения функции.
Графики нечётных функций симметричны относительно
начала координат.

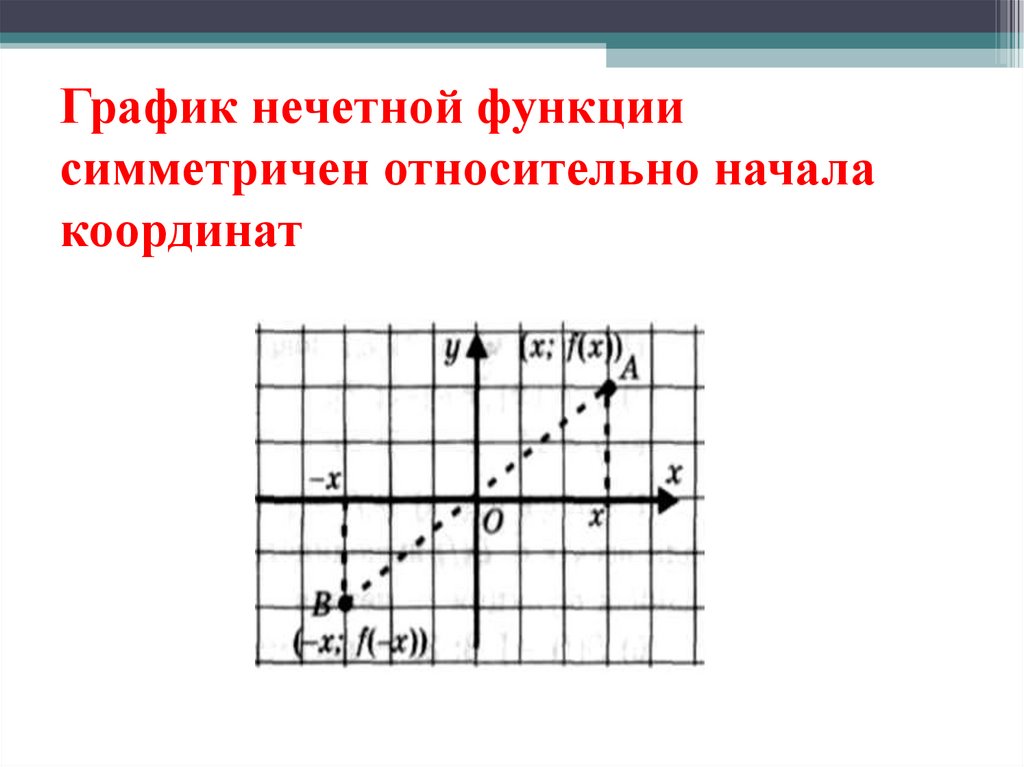
22.

График нечетной функции
симметричен относительно начала
координат

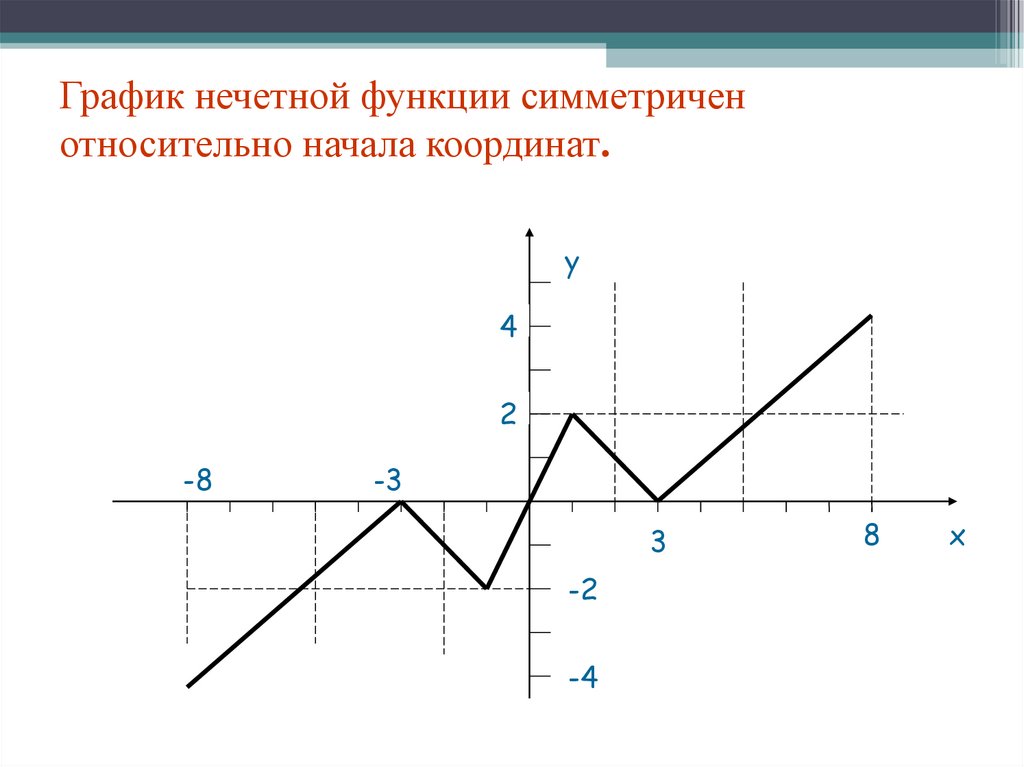
23.

График нечетной функции симметричен
относительно начала координат.
у
4
2
-8
-3
3
-2
-4
8
х

24.

1
3
2
Укажите график нечетной функции.

25.

y
1
0 1
x
1
3
2
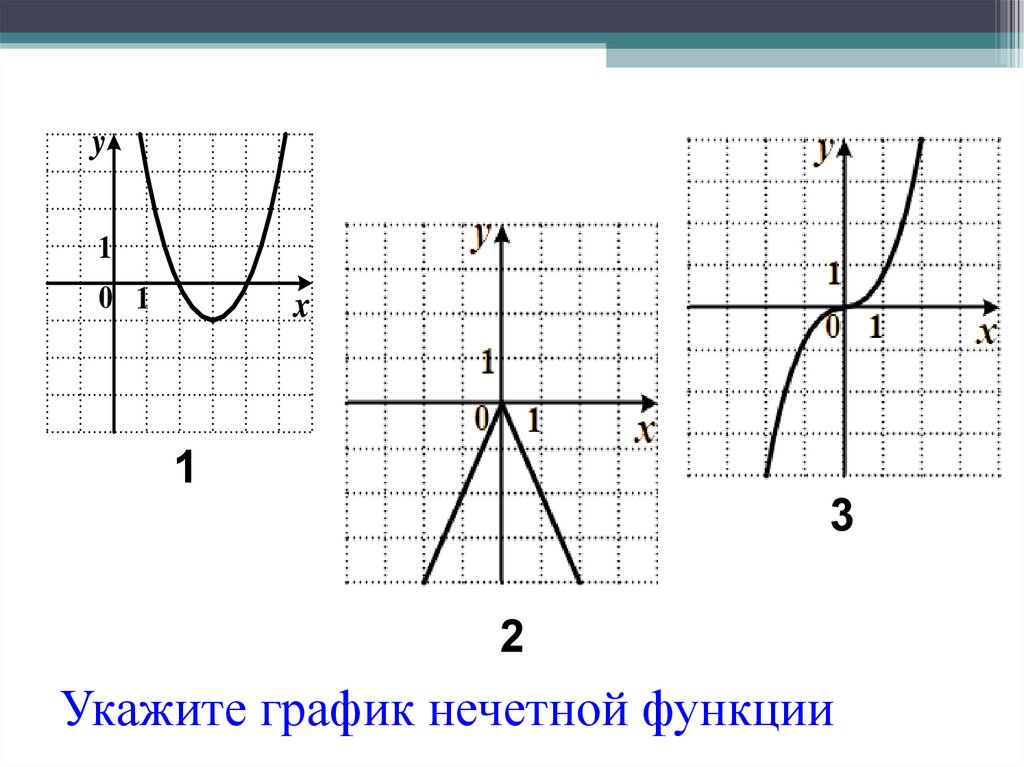
Укажите график нечетной функции

26.

1
3
2
Укажите график нечетной функции.

27.

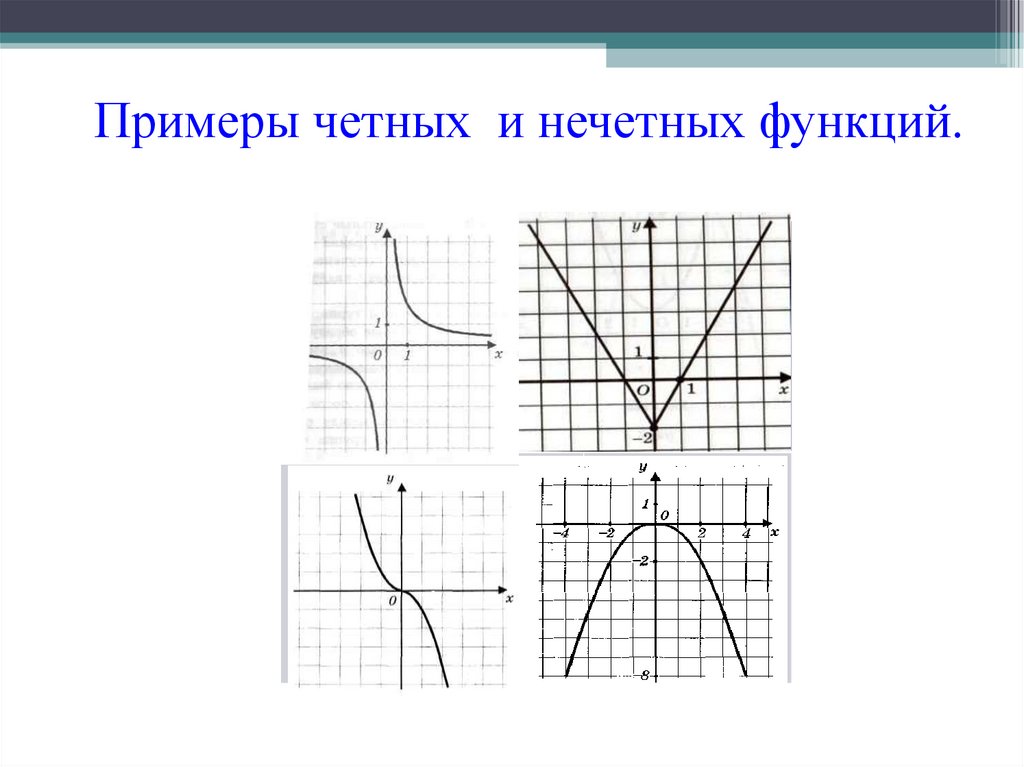
Примеры четных и нечетных функций.

28.

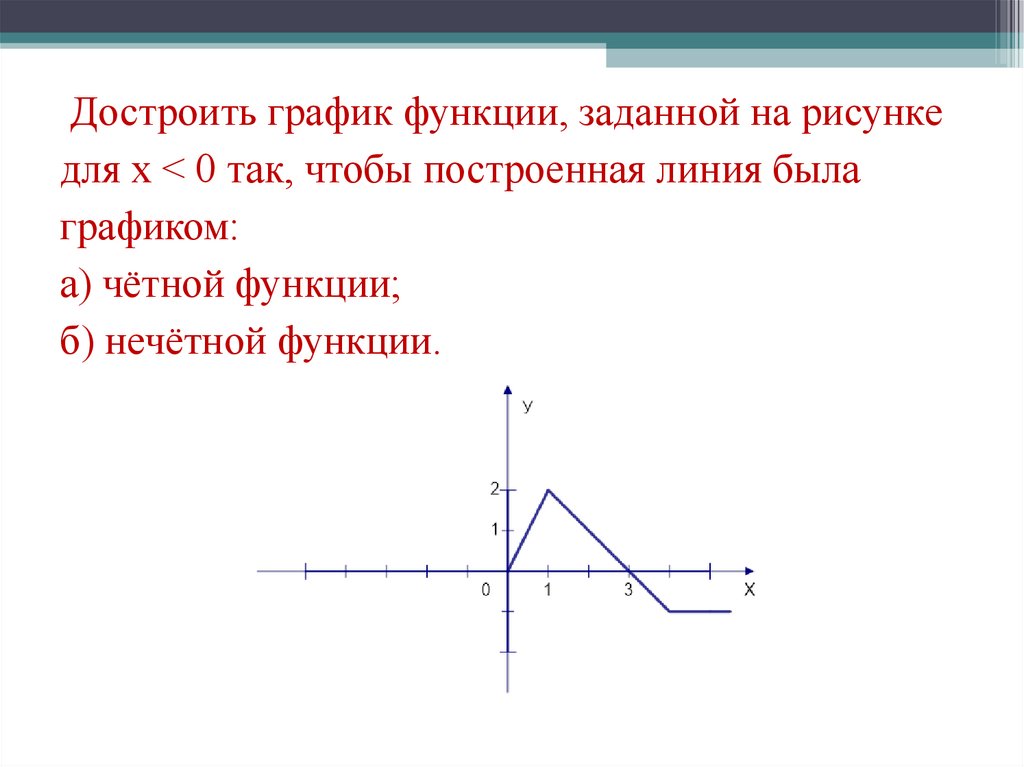
Достроить график функции, заданной на рисунке
для х < 0 так, чтобы построенная линия была
графиком:
а) чётной функции;
б) нечётной функции.

29.

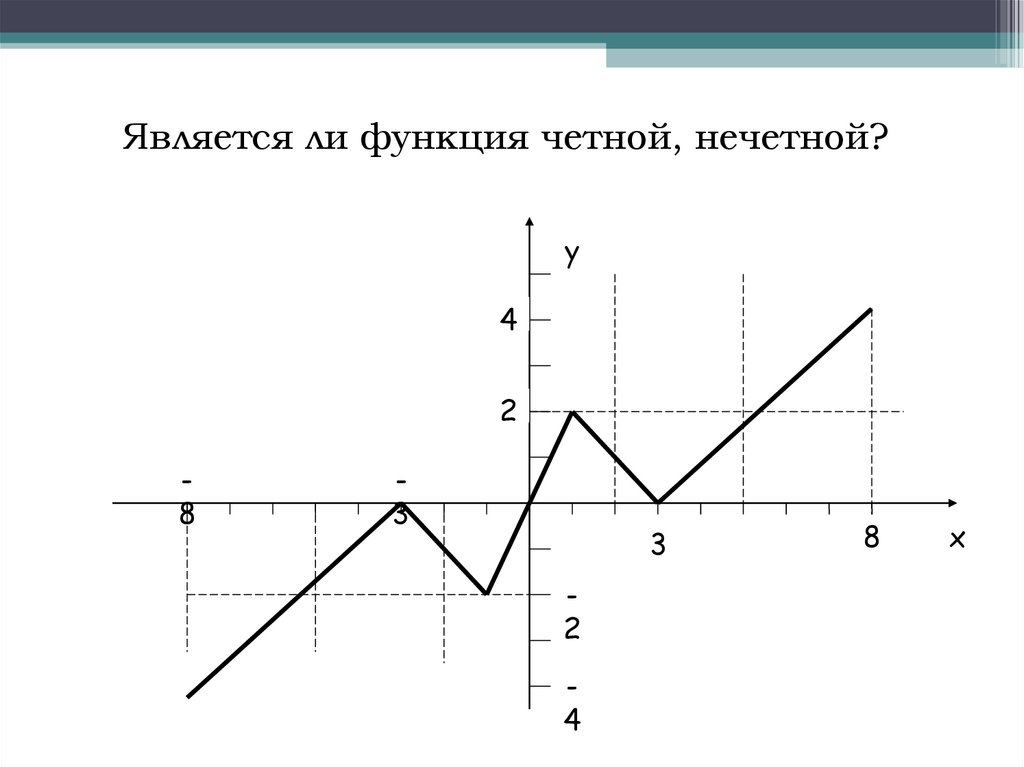
Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х

30.

Является ли функция четной, нечетной?
у
3
7
5
3
3
5
7
х

31.

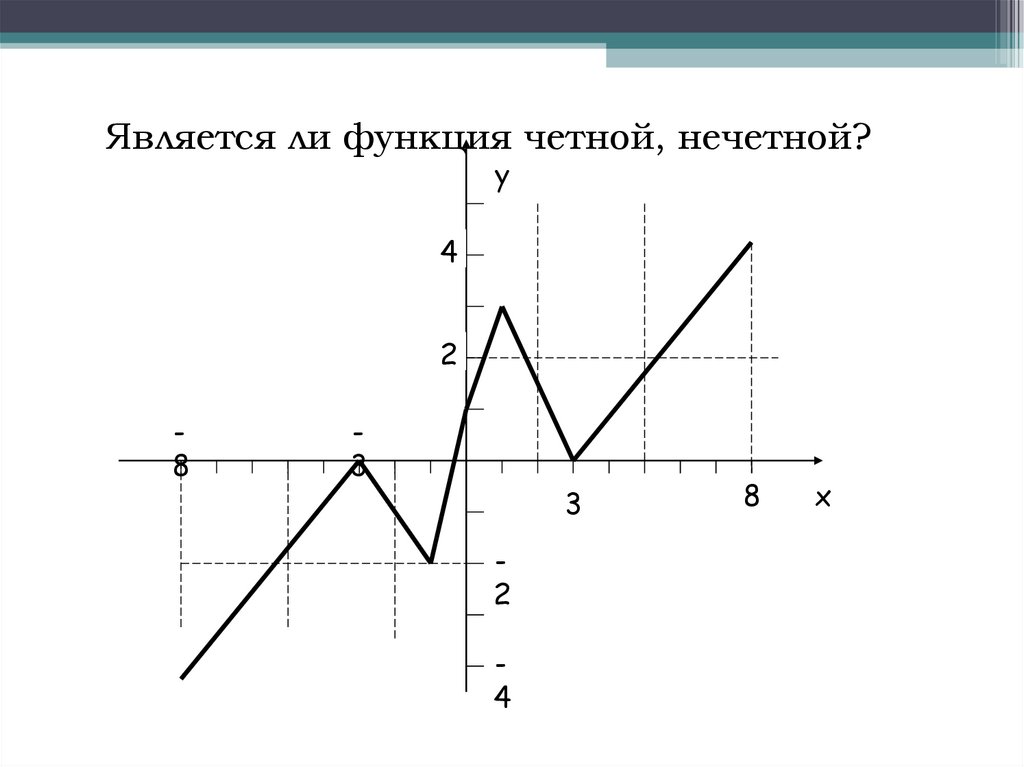
Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х

32.

Повторение
•Найдите область определения, область значений функций.
•Является ли функция четной или нечетной?
у
4
у
2
1
3
5
х
х
4
4
2
2
4
4
4
-

33.

Задание на дом:
• 1.11, 1.19, 1.20