Четность и нечетность функции. (Алгебра 9 класс)

1. Четность и нечетность функции (Алгебра 9 класс)

07.04.2020

2. Цель урока :

Формирование понятий « четность
нечетность функции»; исследование
функций на четность; определение по
графику четных и нечетных функций;
построение графиков функций, содержащих
модуль, используя при этом свойство
четности и нечетности функций.

3. Понятие симметричности

Если числовое множество Х вместе с каждым
своим элементом х содержит и противоположный
элемент – х, то Х называют симметричным
множеством

4. Определите симметричное множество или нет:

1.
2.
3.
4.
5.
6.
7.
8.
(-6; 6),
[ -7; 7],
[0;+ ∞ ),
(-∞;+∞ ),
(-5; 3),
[-5; 5)
(-∞;-2),(2;+∞ )
(-∞;-8),[8;+∞ )

5. Свойства функций

1) Область определения функций .
2) Монотонность функции.
3) Ограниченность функции .
4) Наибольшее и наименьшее значения
функции .
5) Непрерывность .
6) Область значений .
7) Выпуклость
8) Четность, нечетность.

6. Запомнить:

Определение: Функция y(x) называется четной, если
область определения её симметрична относительно
начала координат и выполняется
y(-x) = y(x)
для любого x из области определения этой функции.
График четной функции симметричен относительно оси у.
Определение: Функция y(x) называется нечетной, если
область определения её симметрична относительно
начала координат и выполняется
y(-x) = - y(x)
График нечетной функции симметричен относительно начала
координат.

7. Геометрический смысл свойств чётной и нечётной функций.

8.

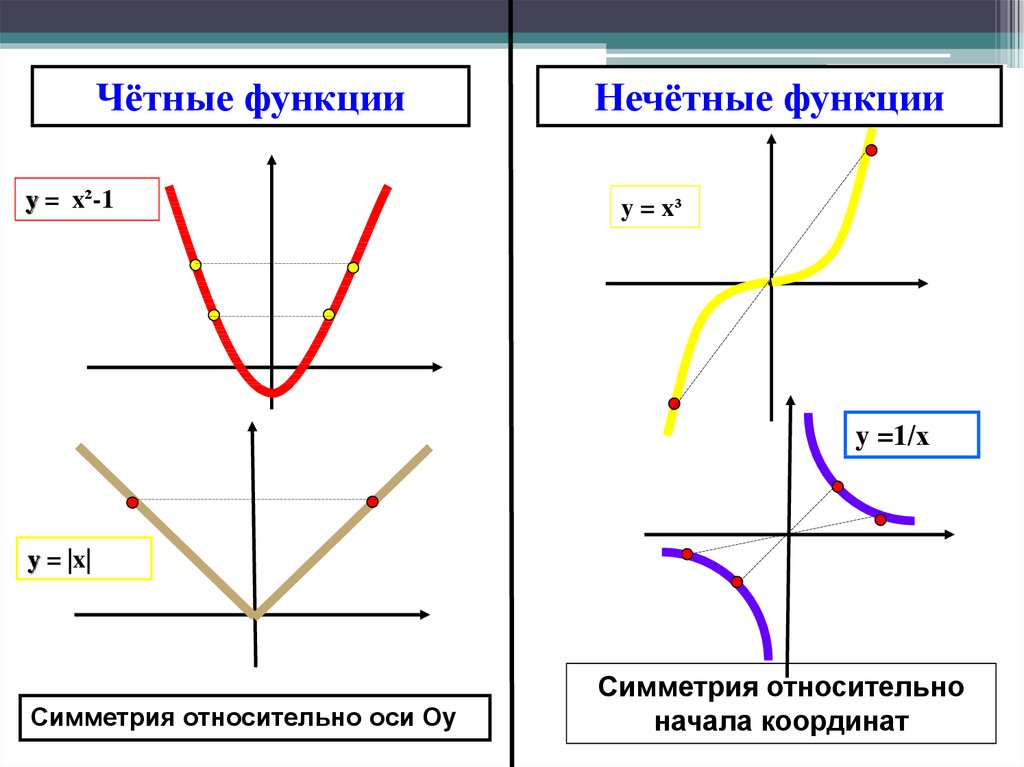
Чётные функции
y = x²-1
Нечётные функции
y = x³
y =1/х
y = |x|
Симметрия относительно оси Оy
Симметрия относительно
начала координат

9. Алгоритм исследования функции на чётность или нечетность

1)Установить , симметрична ли область
определения функции
2) Найти f(-x)
3) Сравнить f(-x) и f(x)

10.

Определение
Чётные функции
Нечётные функции
y (- x) = y (x)
y (- x) = - y (x)
Выяснить является ли функция чётной или нечётной.
y = 5 x²- |X|
Решение:
y (- x)=5 •(- x)² - |- x| =
= 5x² - |x|=
= y (x) - четная
y = 7x +x³
Решение:
y (- x)= 7(- x) +(- x)³=
= - 7 x - x³ =- (7x +x³)=
= - y (x)

11. Примеры: Определите, является ли функция четной или нечетной

1. f(x) =3 x2+x4
2. f(x) = х(5 – x2)
3 . f(x) =4 x6–x2
4.
f(x) = x7+2x3

12. Чётные функции

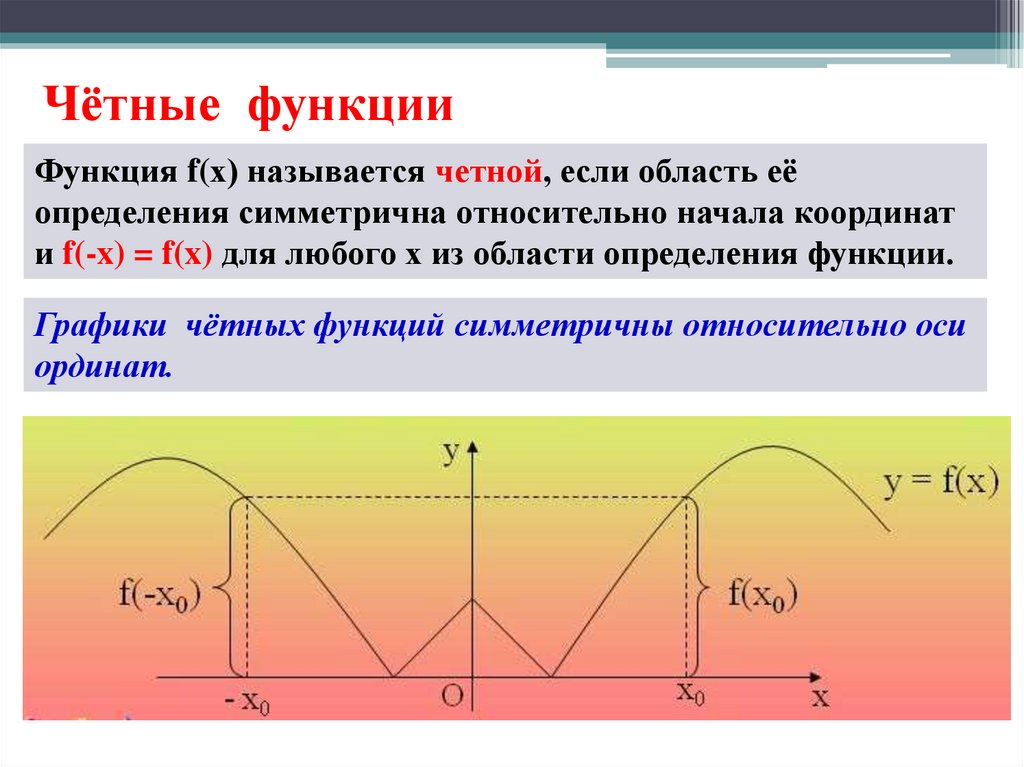
Функция f(х) называется четной, если область её
определения симметрична относительно начала координат
и f(-x) = f(x) для любого х из области определения функции.
Графики чётных функций симметричны относительно оси
ординат.

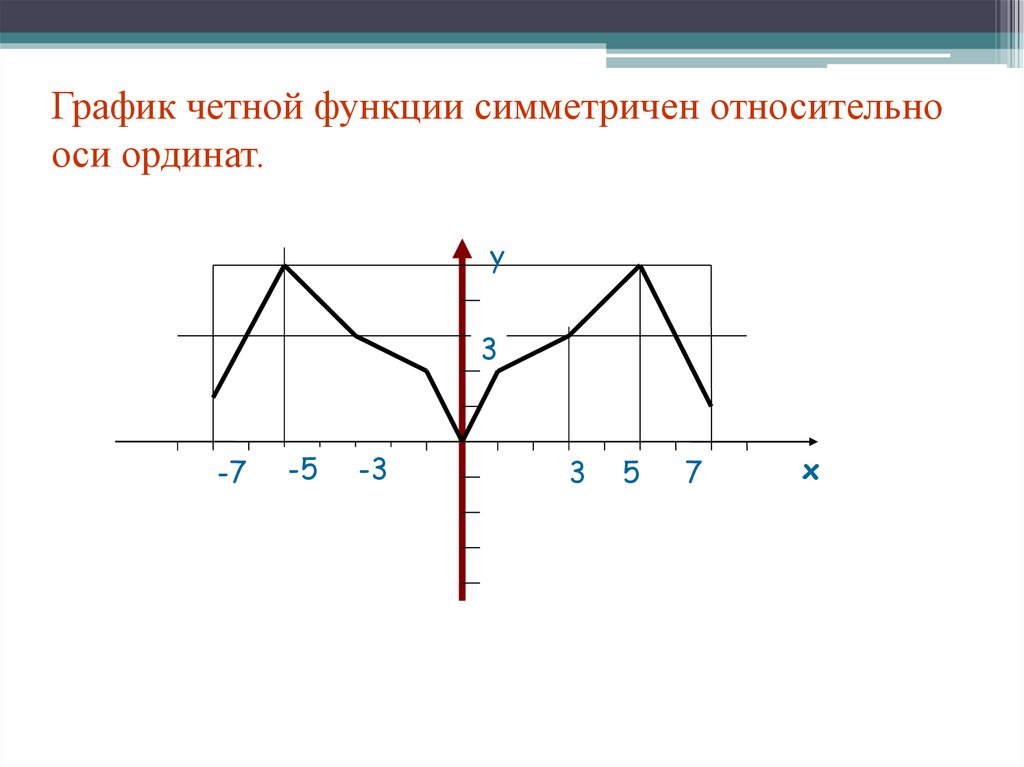
13. График четной функции симметричен отно­сительно оси ординат

График четной функции симметричен
относительно оси ординат

14. График четной функции симметричен относительно оси ординат.

у
3
-7
-5
-3
3
5
7
х

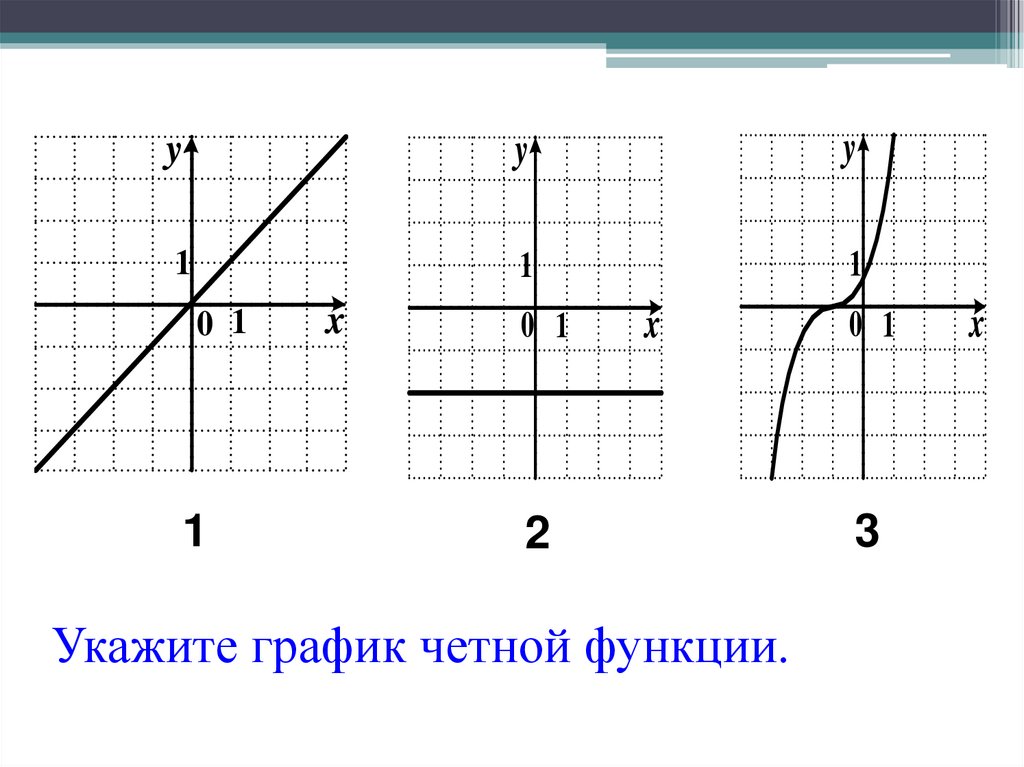
15. Укажите график четной функции.

y
y
y
1
1
1
0 1
1
x
0 1
x
2
Укажите график четной функции.
0 1
3
x

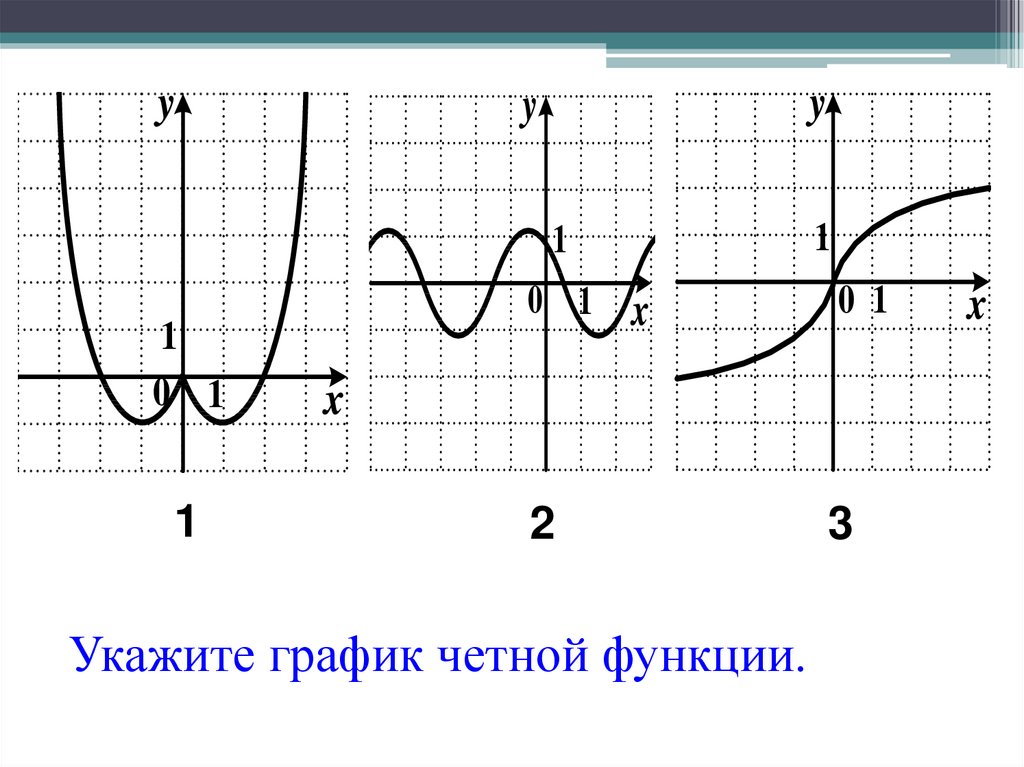
16. Укажите график четной функции.

y
y
y
1
1
0 1
1
1
0 1 x
0 1
2
3
x
Укажите график четной функции.
x

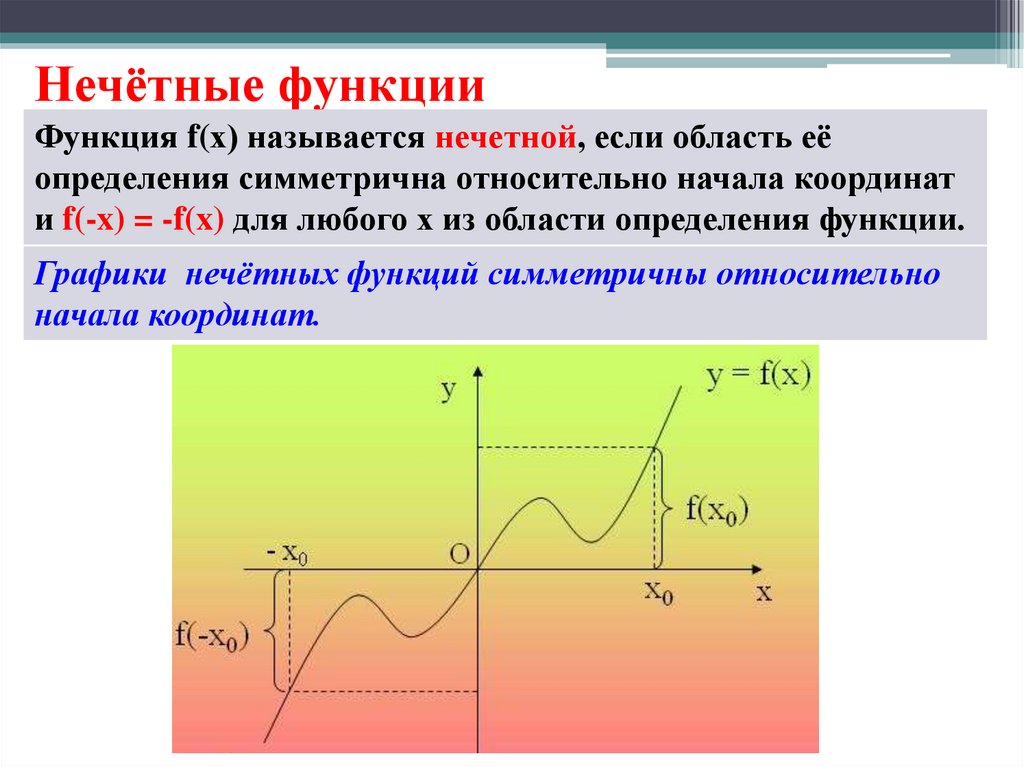
17. Нечётные функции

Функция f(х) называется нечетной, если область её
определения симметрична относительно начала координат
и f(-x) = -f(x) для любого х из области определения функции.
Графики нечётных функций симметричны относительно
начала координат.

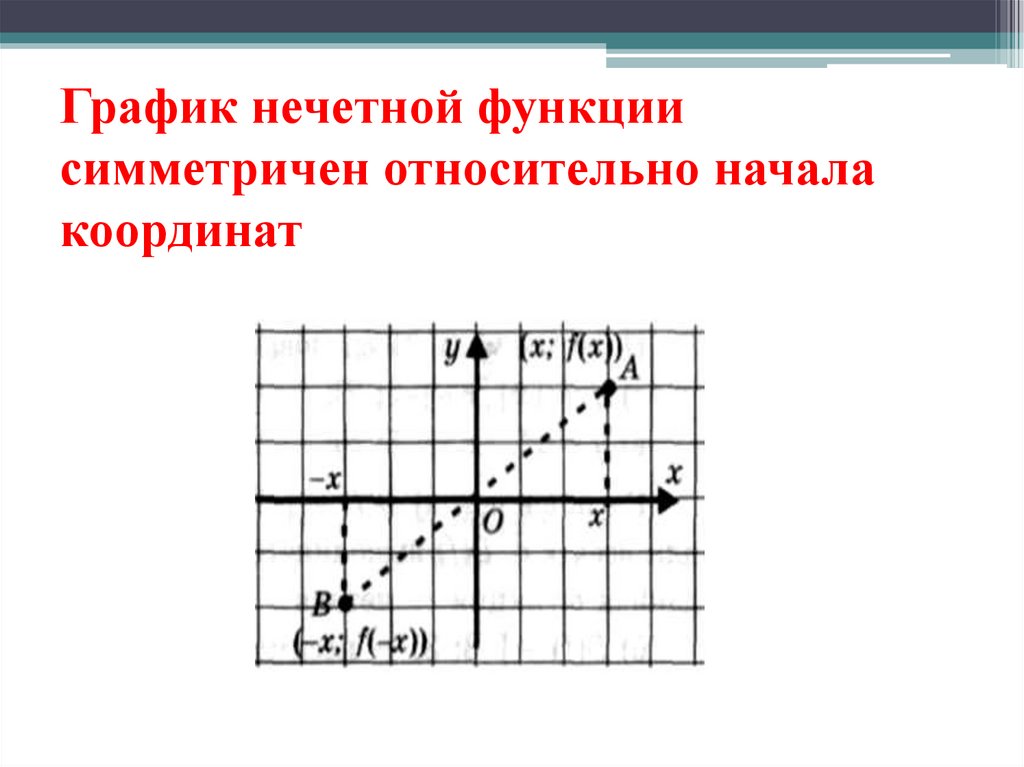
18. График нечетной функции симметричен относительно начала координат

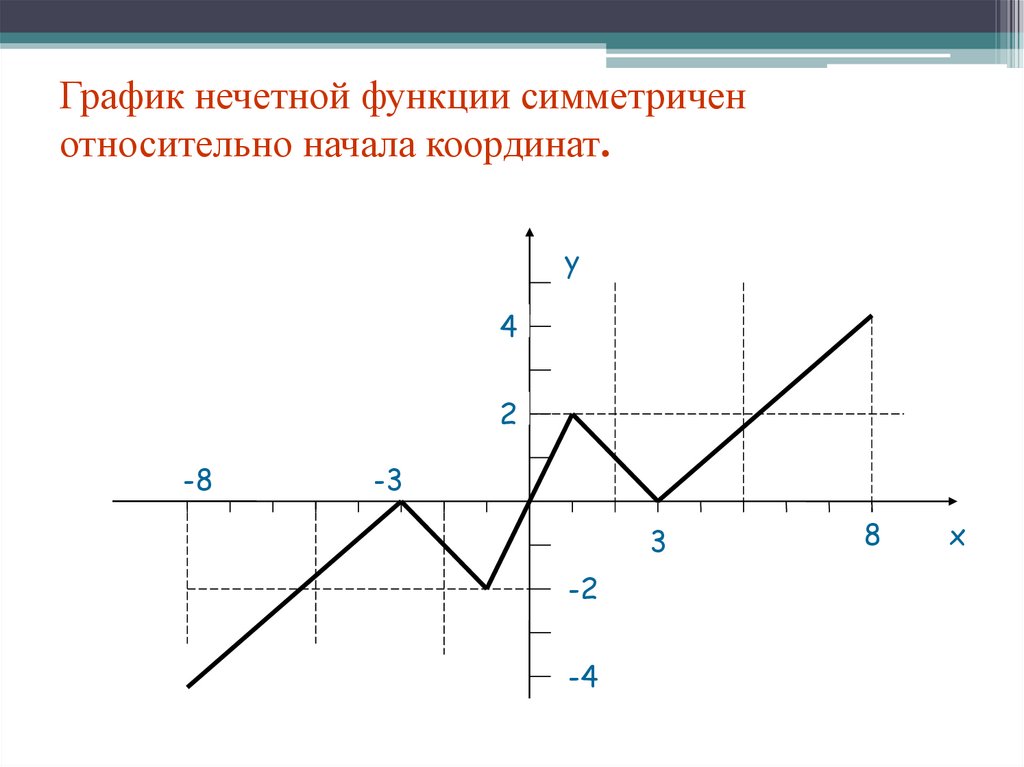
19. График нечетной функции симметричен относительно начала координат.

у
4
2
-8
-3
3
-2
-4
8
х

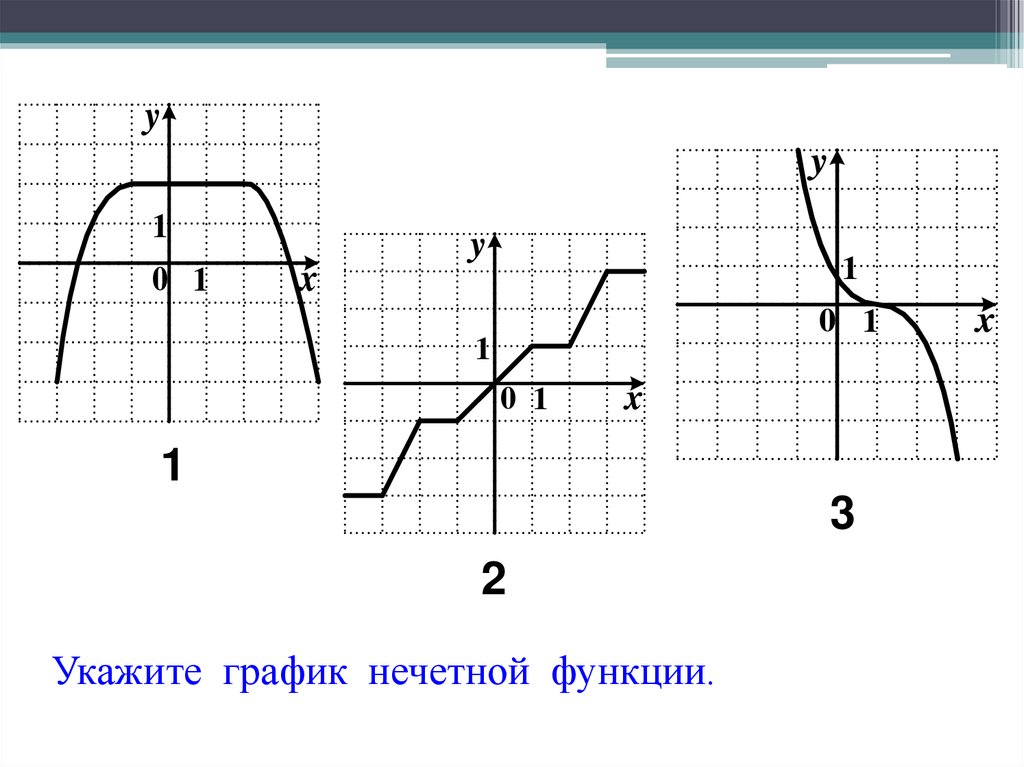
20. Укажите график нечетной функции.

y
y
1
0 1
y
1
x
0 1
1
0 1
x
1
3
2
Укажите график нечетной функции.
x

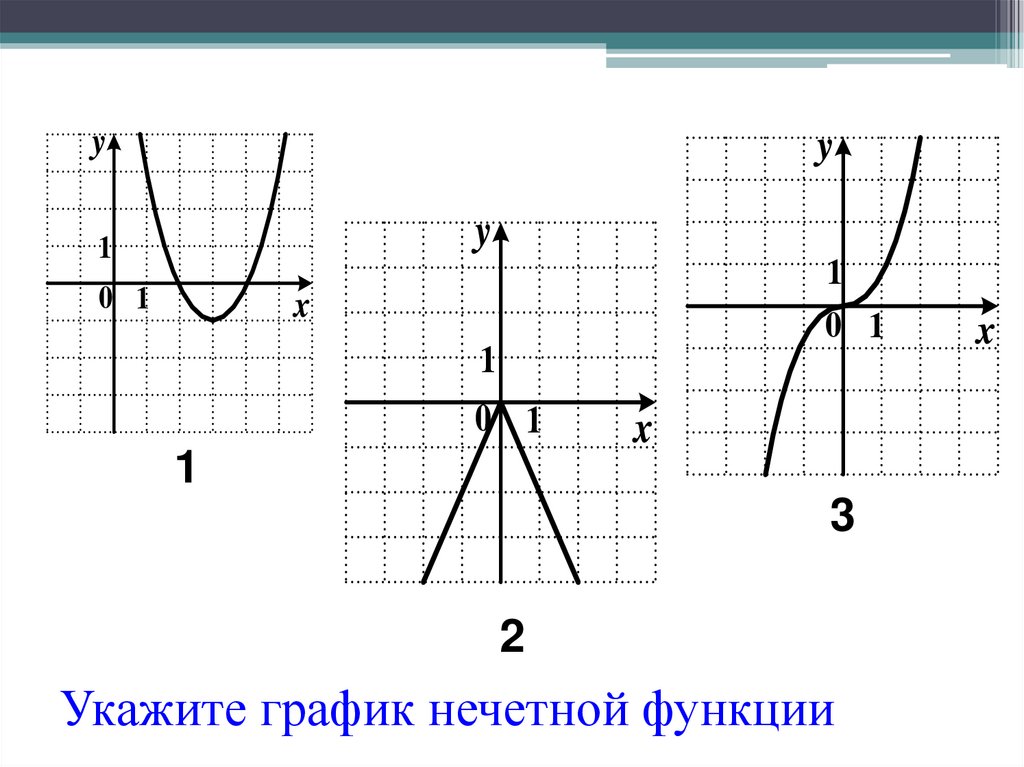
21. Укажите график нечетной функции

y
y
y
1
0 1
1
0 1
x
1
0 1
1
x
3
2
Укажите график нечетной функции
x

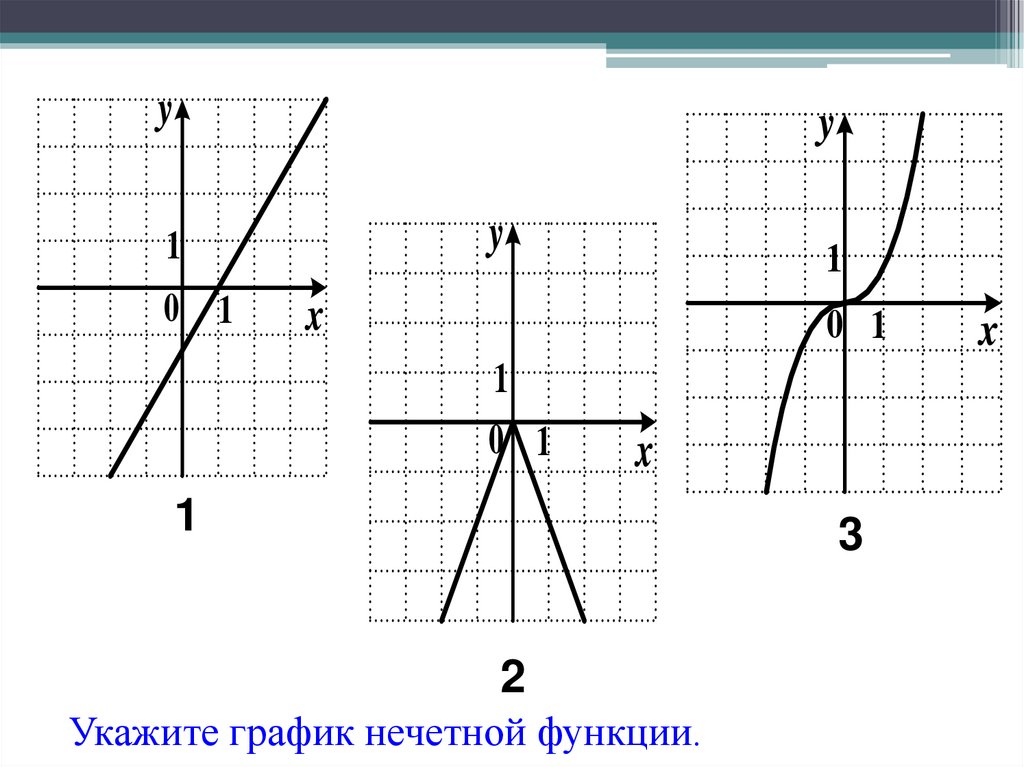
22. Укажите график нечетной функции.

y
y
y
1
0 1
1
x
0 1
1
0 1
x
1
3
2
Укажите график нечетной функции.
x

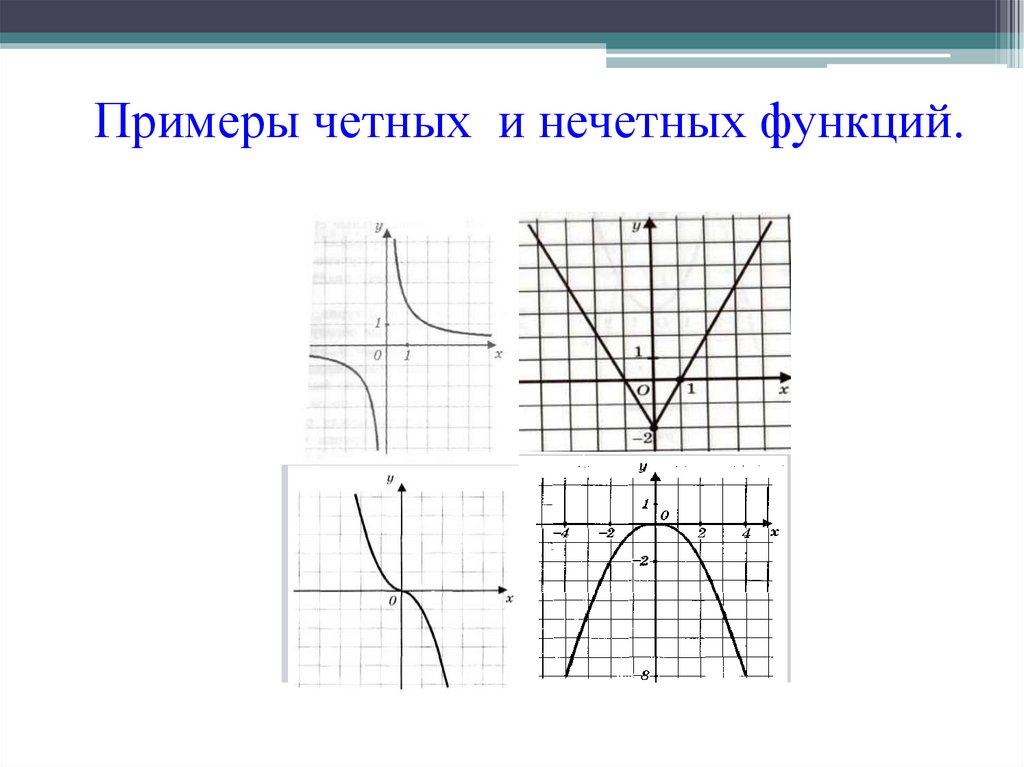
23. Примеры четных и нечетных функций.

24. Достроить график функции, заданной на рисунке для х < 0 так, чтобы построенная линия была графиком: а) чётной функции; б)

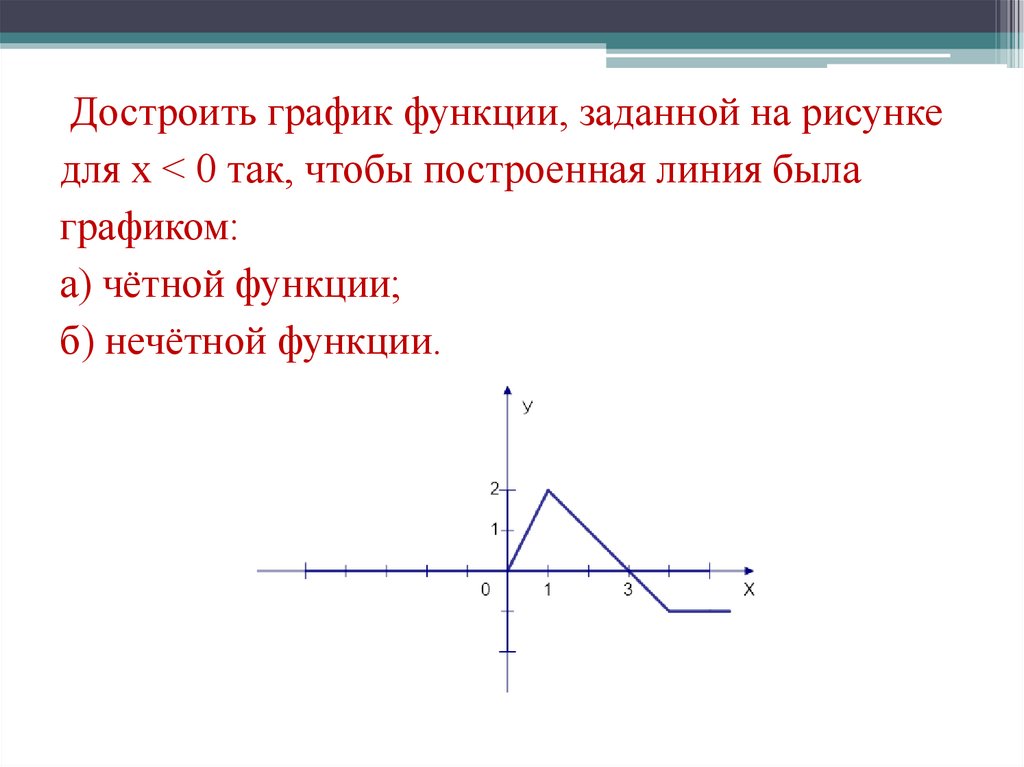
Достроить график функции, заданной на рисунке
для х < 0 так, чтобы построенная линия была
графиком:
а) чётной функции;
б) нечётной функции.

25.

Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х

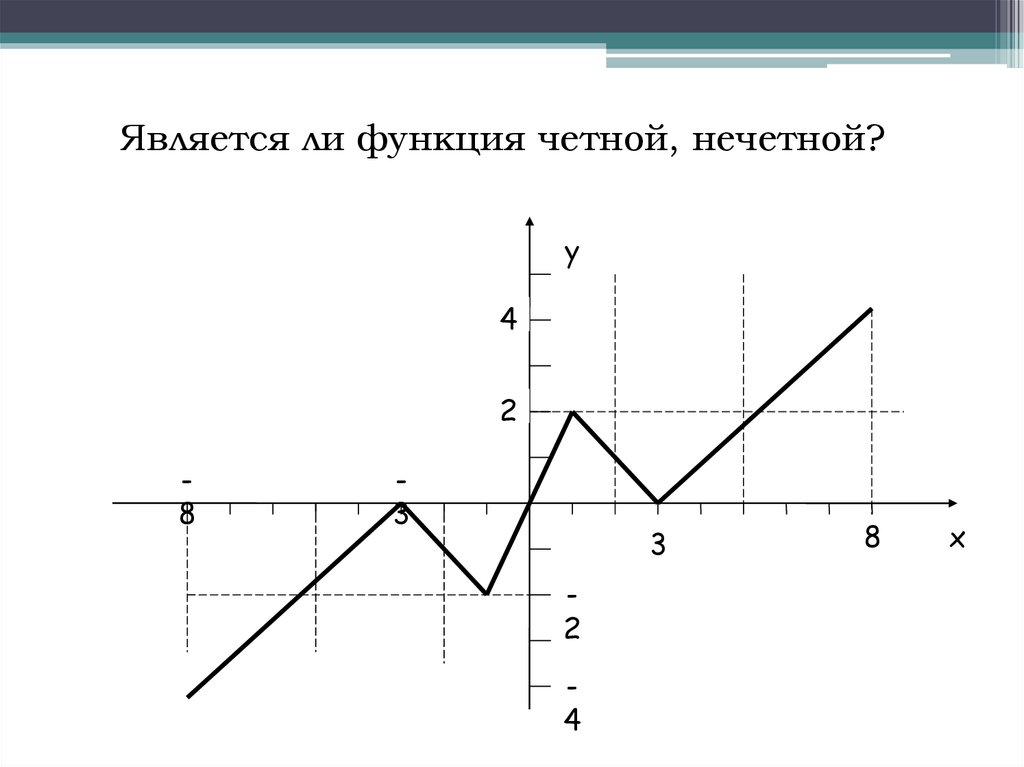
26.

Является ли функция четной, нечетной?
у
3
7
5
3
3
5
7
х

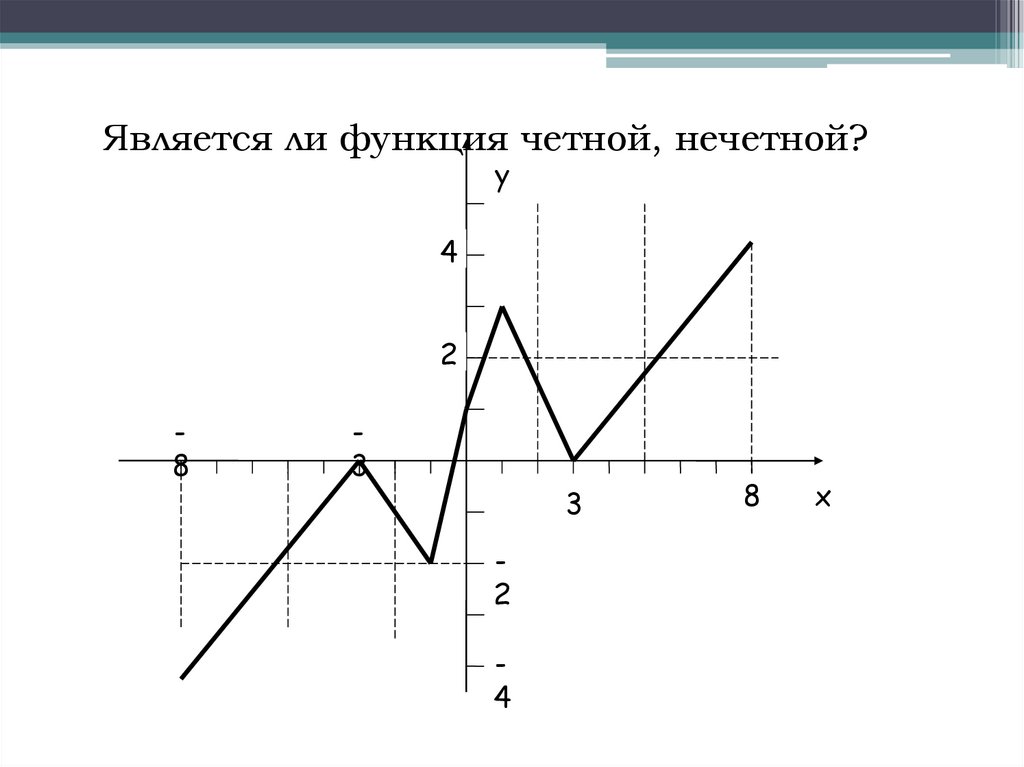
27.

Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х

28.

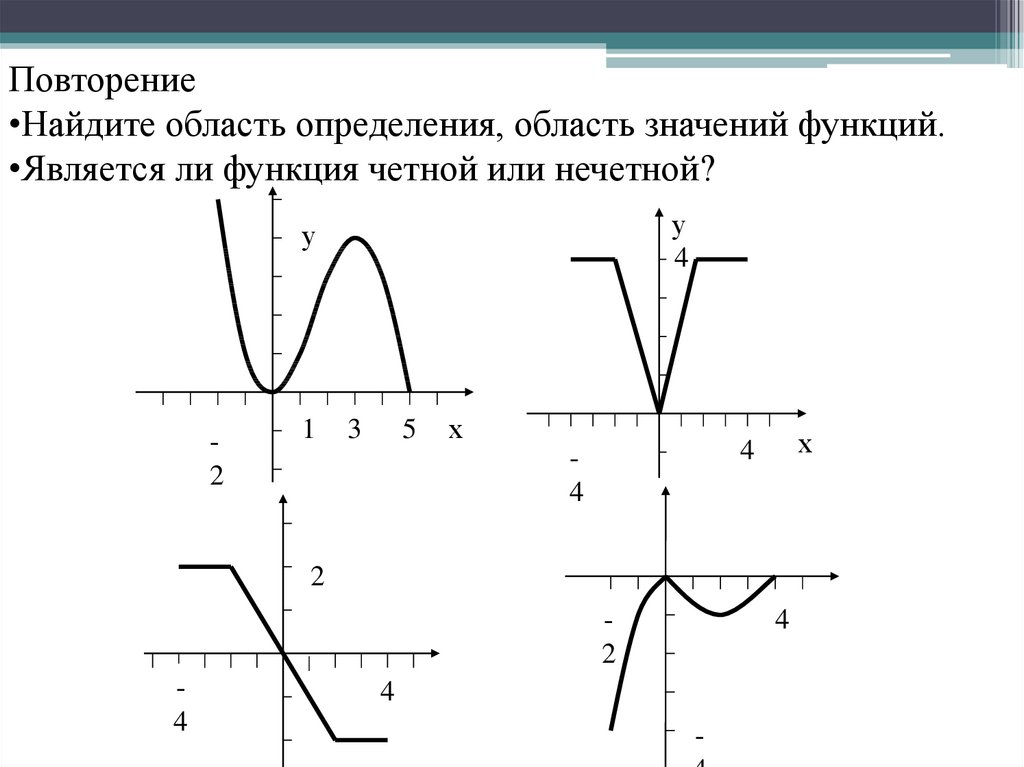
Повторение
•Найдите область определения, область значений функций.
•Является ли функция четной или нечетной?
у
4
у
2
1
3
5
х
х
4
4
2
2
4
4
4
-