Лекция 7. Сплайны

1. Сплайны. Кривые и поверхности

Компьютерная графика

2. Представление кривых на плоскости

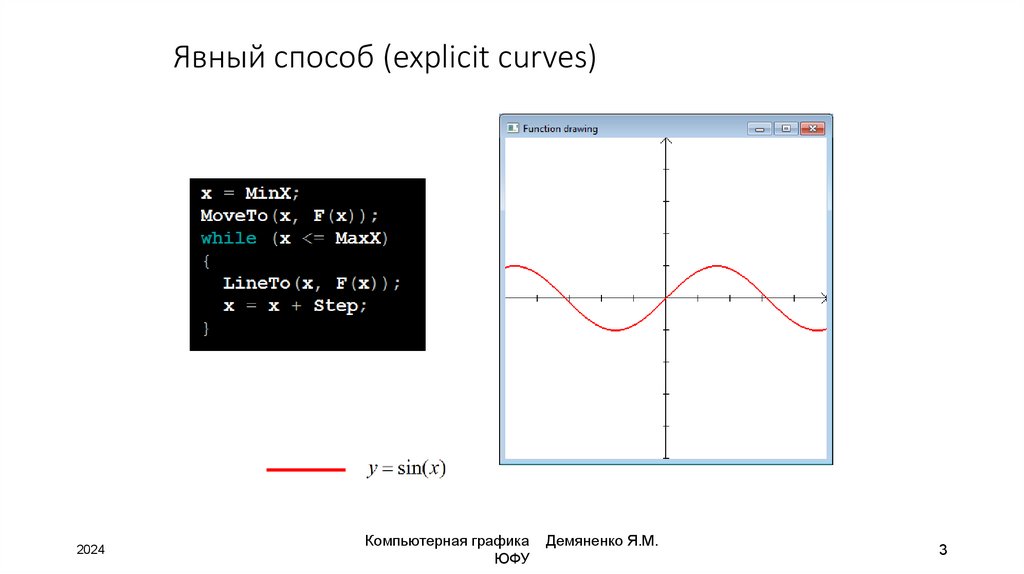
• явный способ (explicit curves)
• неявный способ (implicit)
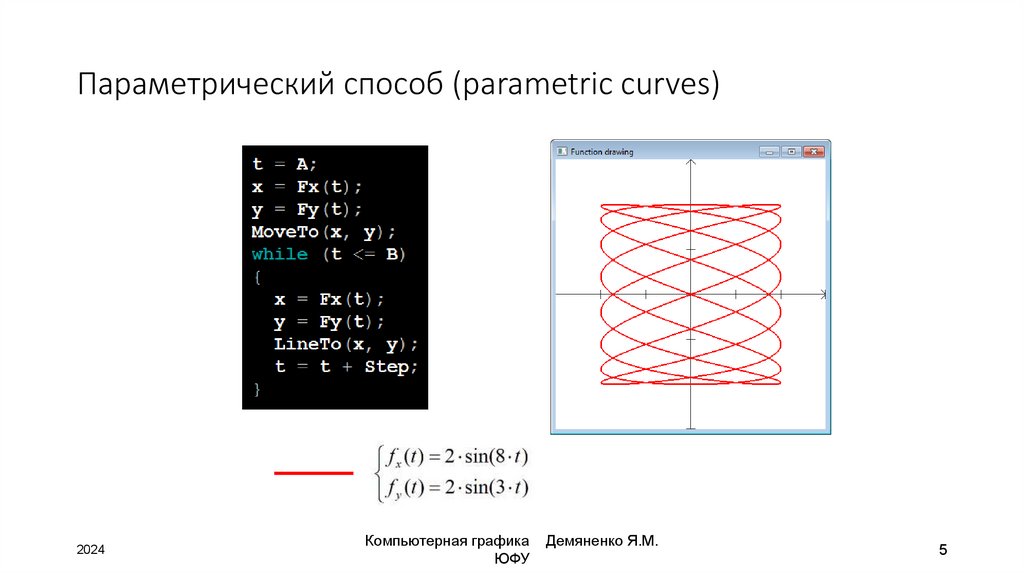
• параметрический способ (parametric curves)
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
2

3. Явный способ (explicit curves)

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
3

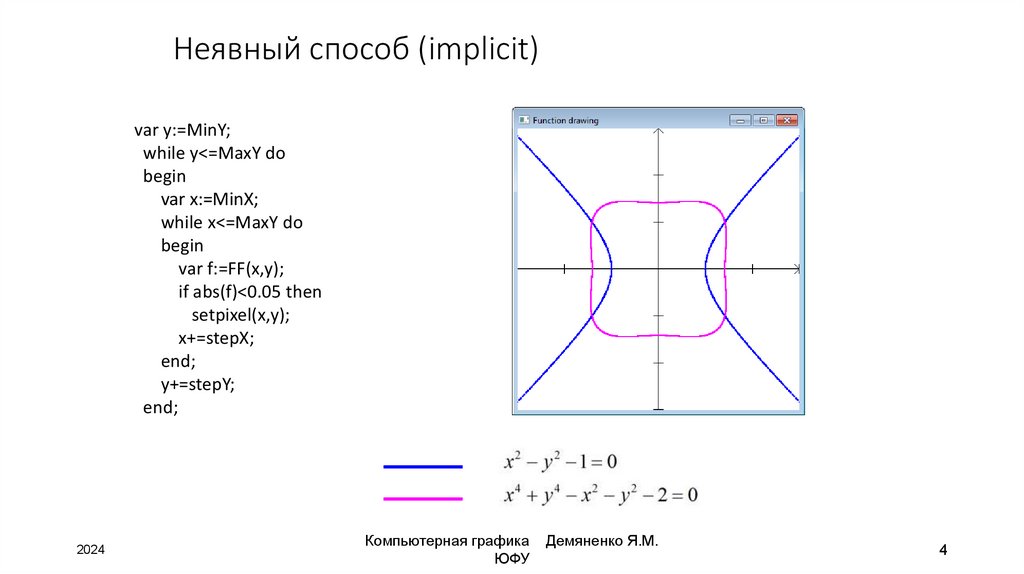
4. Неявный способ (implicit)

var y:=MinY;
while y<=MaxY do
begin
var x:=MinX;
while x<=MaxY do
begin
var f:=FF(x,y);
if abs(f)<0.05 then
setpixel(x,y);
x+=stepX;
end;
y+=stepY;
end;
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
4

5. Параметрический способ (parametric curves)

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
5

6. А если вид функции неизвестен?

2024
Компьютерная графика Демяненко Я.М. ЮФУ
6

7. А если вид функции неизвестен?

А что известно?
2024
Компьютерная графика Демяненко Я.М. ЮФУ
7

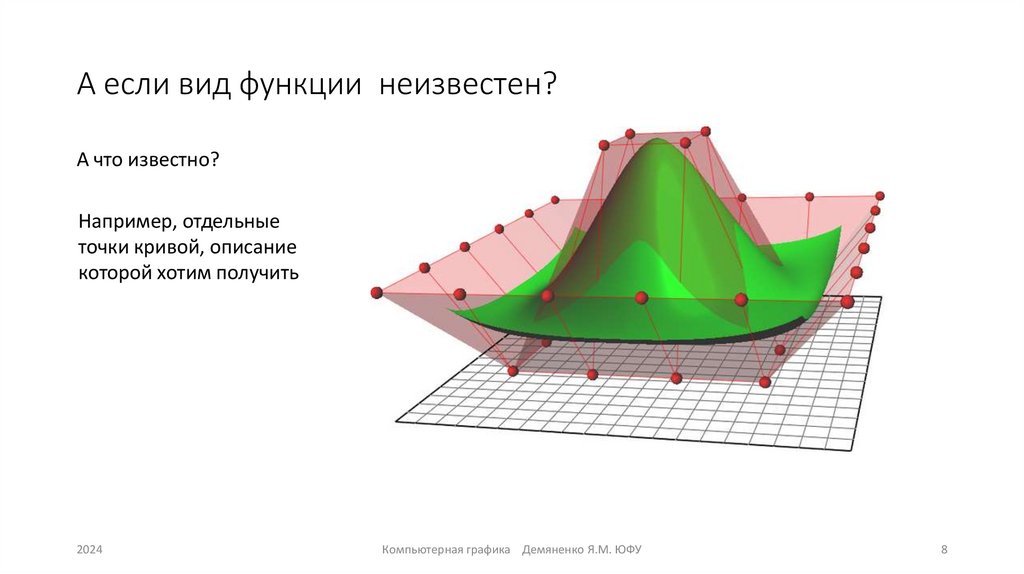
8. А если вид функции неизвестен?

А что известно?
Например, отдельные
точки кривой, описание
которой хотим получить
2024
Компьютерная графика Демяненко Я.М. ЮФУ
8

9. Кривые Безье или Кривые Бернштейна-Безье

60-е годы XX века
• Пьер Безье (Pierre Bézier) из автомобилестроительной компании «Рено»
• Поль де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен»
• Сергей Натанович Бернштейн
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
9

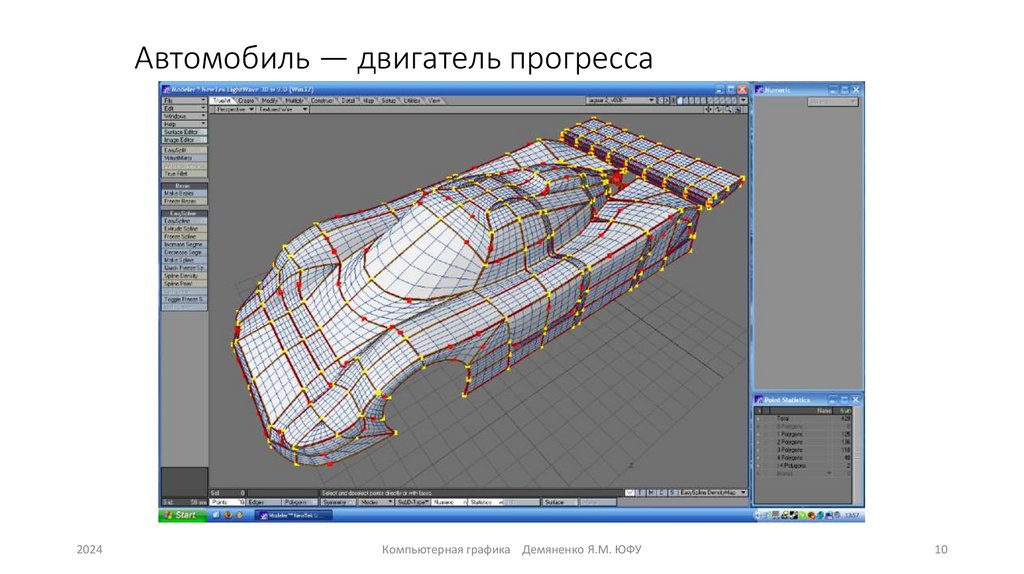
10. Автомобиль — двигатель прогресса

2024
Компьютерная графика Демяненко Я.М. ЮФУ
10

11. Пьер Безье (Pierre Bézier)

Французский инженер и
патентообладатель кривых Безье и поверхностей Безье
1962 год
В компании Рено (1933 - 1975 )
разработал компьютерную систему
проектирования UNISURF,
предназначенную для
проектирования кузовов
автомобилей.
В 1985 году получил награду от
ACM SIGGRAPH за
пожизненный вклад в
компьютерную графику и
интерактивную технику.
1 сентября 1910 г - 25 ноября 1999 г.
(89 лет)
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
11

12. Поль де Кастельжо

1959
Производственная тайна до
конца 1960-х
Компания Citroen
Рекурсивный способ определения
кривых (алгоритм де Кастельжо)
19 ноября 1930 - 24 марта 2022
(91 год)
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
12

13. Бернштейн, Сергей Натанович

советский математик
Кривые Безье – частный
случай многочленов
Бернштейна,
описанных Сергеем
Натановичем Бернштейном в
1912 году
При доказательстве аппроксимационной
теоремы Вейерштрасса Бернштейном были
построены полиномы, оказавшиеся полезными
в самых разных областях математики.
Теперь их называют полиномами Бернштейна.
5 марта 1880 — 26 октября 1968
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
13

14. Кривые Безье (Pierre Bézier): линейные

• Линейная интерполяция между концевыми точками
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
14

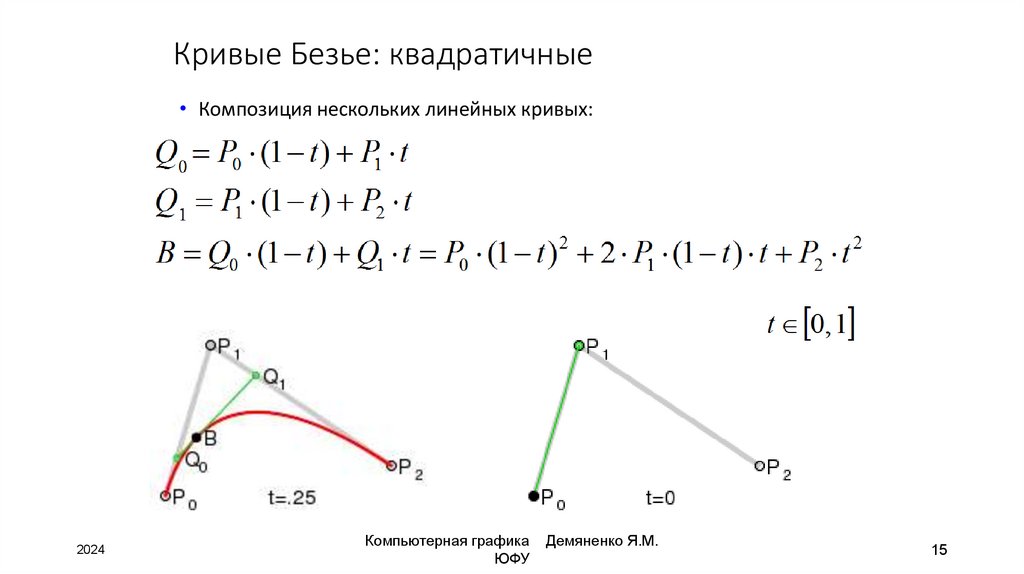
15. Кривые Безье: квадратичные

• Композиция нескольких линейных кривых:
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
15

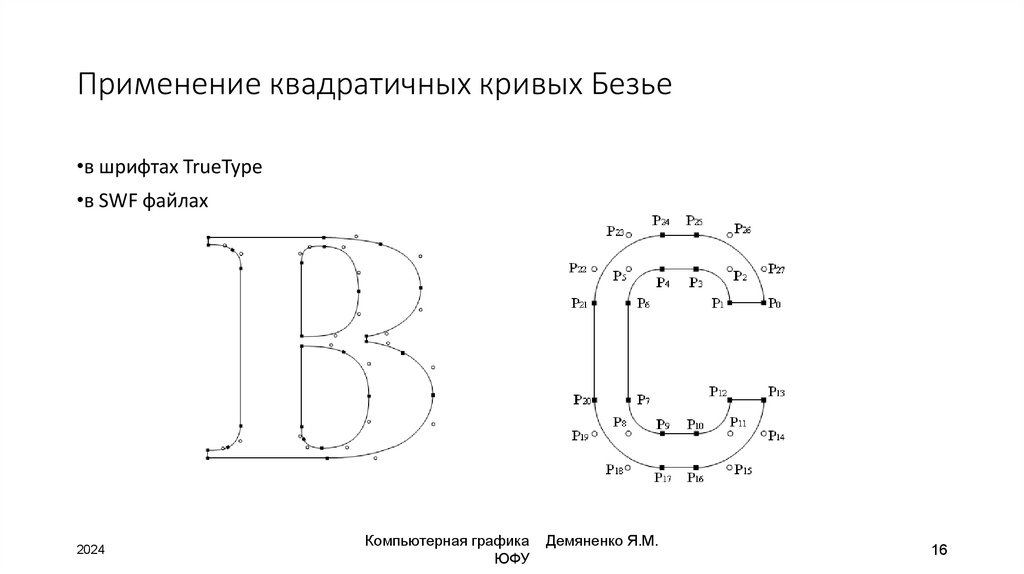
16. Применение квадратичных кривых Безье

•в шрифтах TrueType
•в SWF файлах
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
16

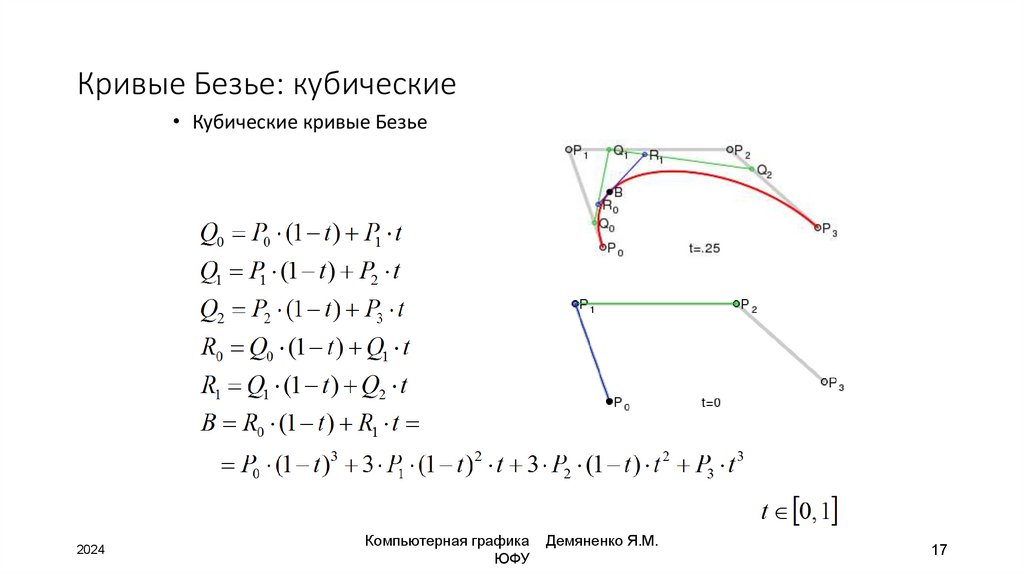
17. Кривые Безье: кубические

• Кубические кривые Безье
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
17

18. Применение кривых Безье

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
18

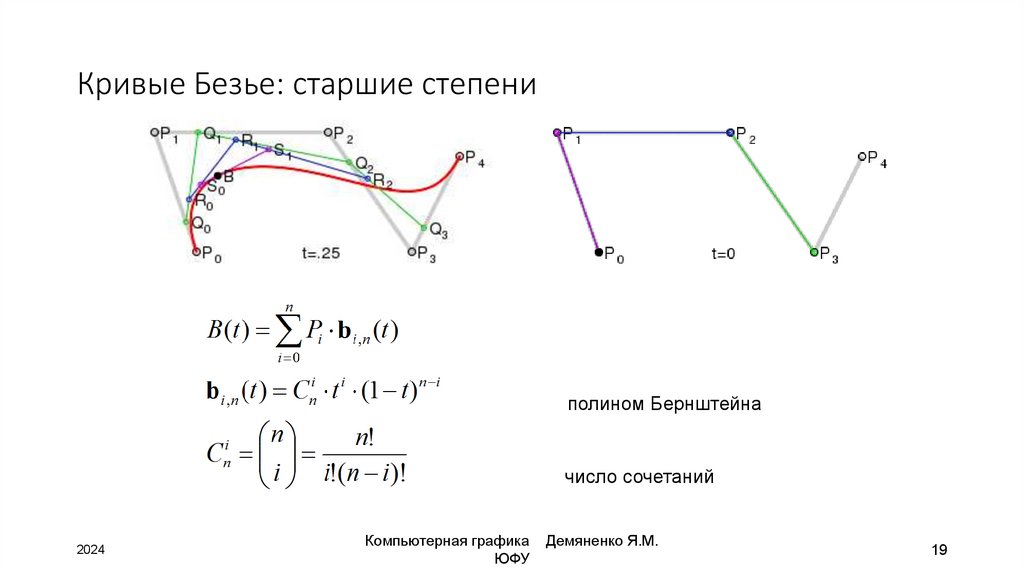
19. Кривые Безье: старшие степени

полином Бернштейна
число сочетаний
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
19

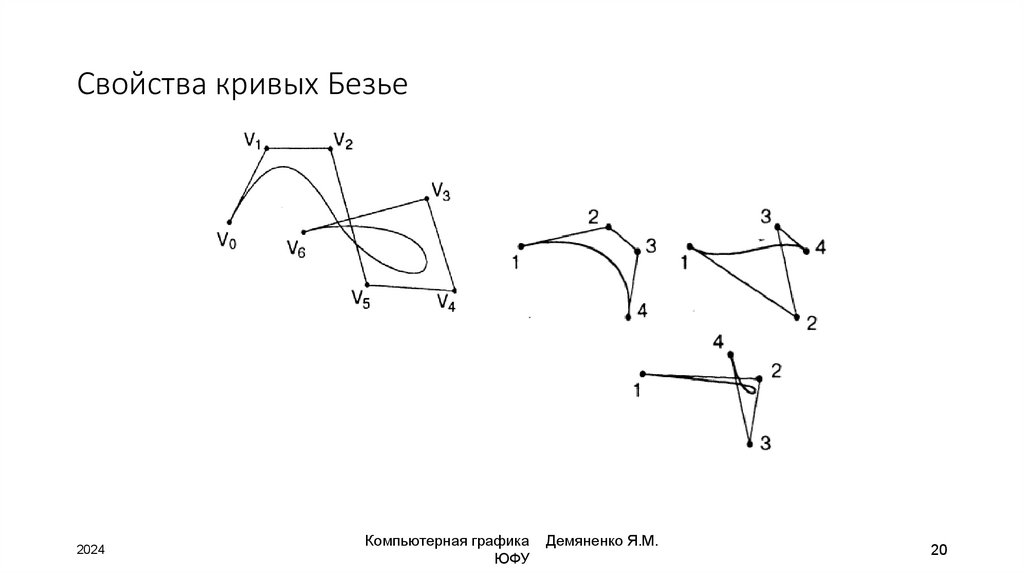
20. Свойства кривых Безье

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
20

21. Кубические кривые Безье: матричная запись

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
21

22. Кубические сплайны Эрмита

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
22

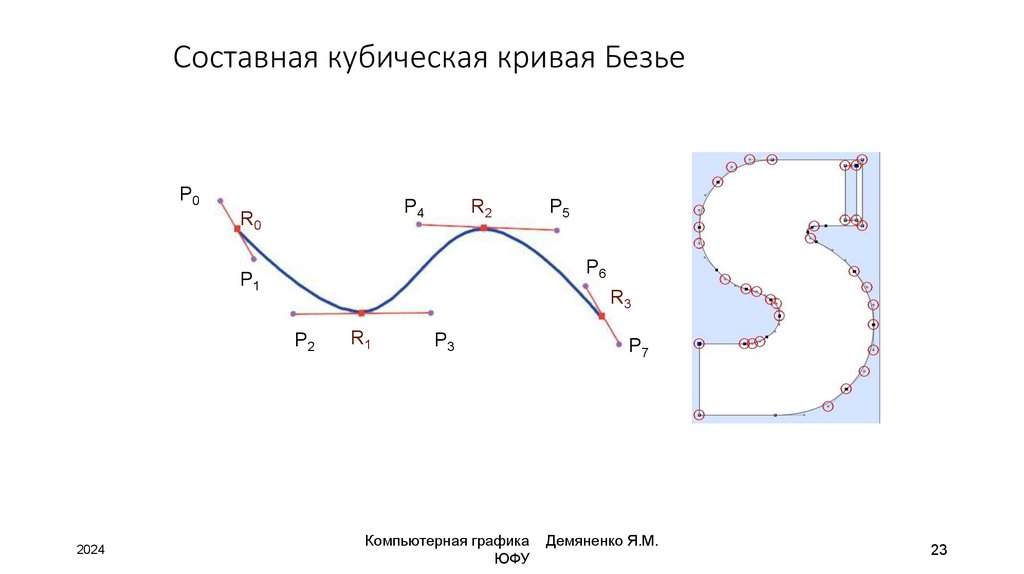
23. Составная кубическая кривая Безье

P0
P4
R0
R2
P6
P1
R3
P2
2024
P5
R1
P3
Компьютерная графика
ЮФУ
P7
Демяненко Я.М.
23

24. Составная кубическая кривая Безье

V0 ,V1 ,...,Vm 1 ,Vm
V3i 1 ,V3i ,V3i 1
Точки составной кривой Безье
Каждые 3 точки лежат на одной прямой
V2i 1 , V3i 1 V0i , V1i
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
24

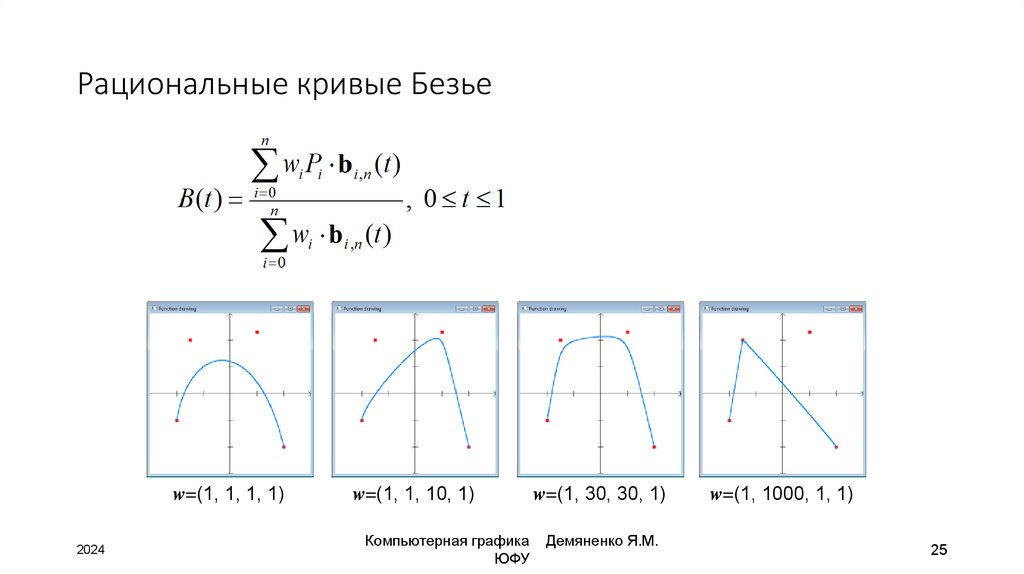
25. Рациональные кривые Безье

w=(1, 1, 1, 1)
2024
w=(1, 1, 10, 1)
Компьютерная графика
ЮФУ
w=(1, 30, 30, 1)
Демяненко Я.М.
w=(1, 1000, 1, 1)
25

26. B-сплайны

• B-сплайны обладают двумя преимуществами по сравнению со сплайнами Безье:
• во-первых, степень полинома B-сплайна можно задать независимо от числа
контрольных точек (с определенными ограничениями);
• во-вторых, B-сплайны допускают локальный контроль над формой кривой.
• Платой за это является бОльшая сложность B-сплайнов по сравнению со сплайнами Безье.
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
26

27. B-сплайны

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
27

28. Неоднородный рациональный B-сплайн, NURBS

• В 1960-х было установлено, что неравномерные рациональные B-сплайны являются
обобщением сплайнов Безье, которые могут быть определены как равномерные
рациональные B-сплайны.
• Первой работой с упоминанием NURBS стала диссертация Кена Версприла (Ken Versprille),
аспиранта Сиракузского университета в Нью-Йорке [Versprille 1975].
• Интерактивная отрисовка кривых и поверхностей NURBS в реальном времени стала
впервые доступна на рабочих станциях Silicon Graphics в 1989 году
Maya, 3ds Max, Blender
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
28

29. Представление поверхностей

• явный способ (explicit curves)
• неявный способ (implicit)
• параметрический способ (parametric curves)
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
29

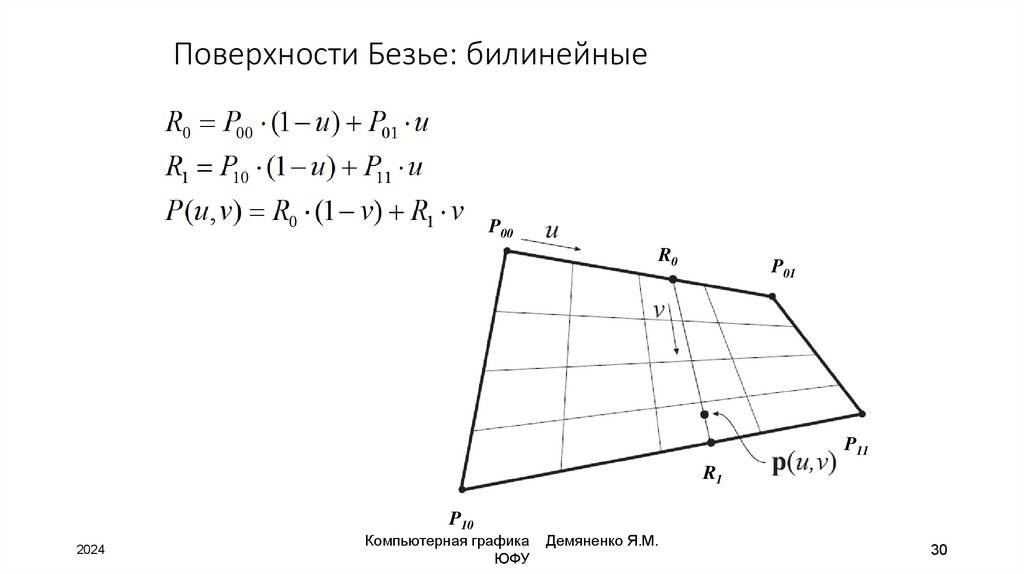
30. Поверхности Безье: билинейные

P00
R0
P01
P11
R1
P10
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
30

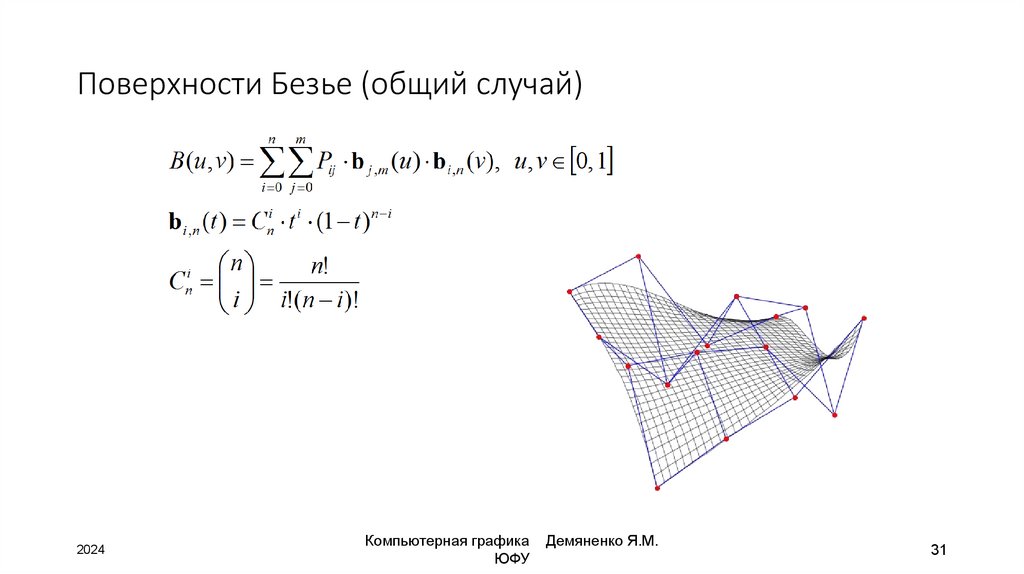
31. Поверхности Безье (общий случай)

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
31

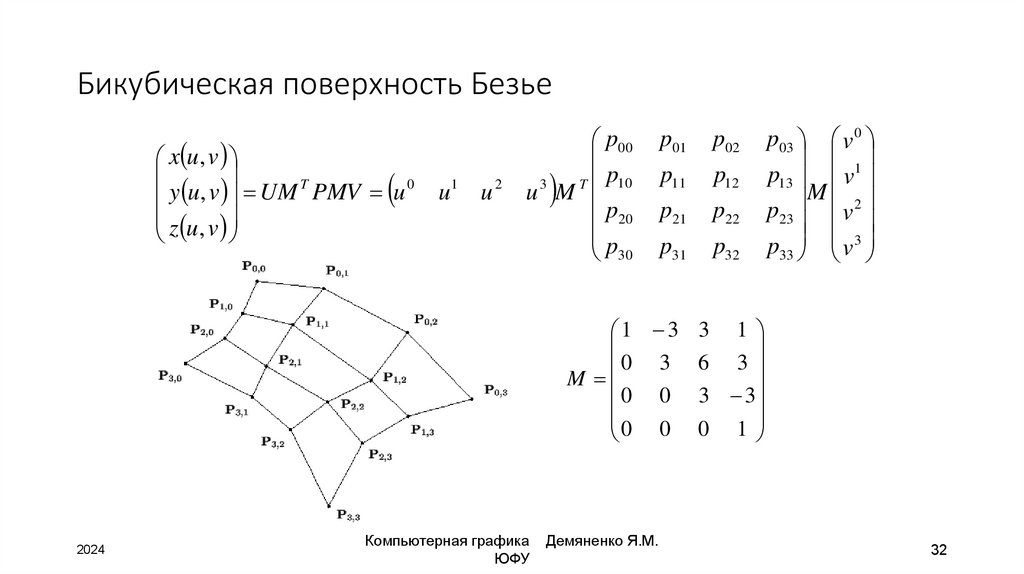
32. Бикубическая поверхность Безье

x u, v
T
0
y
u
,
v
UM
PMV
u
z u, v
u1 u 2
p00
p
3
T 10
u M
p
20
p
30
p01
p11
p21
p31
1 3
0 3
M
0 0
0 0
2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
p02
p12
p22
p32
p03 v 0
1
p13 v
M 2
p23
v
p33 v 3
3 1
6 3
3 3
0 1
32

33. Бикубическая поверхность Безье: сопряжение

Pij1 , i 0,1,2,3; j 0,1,2,3
Pij2 , i 0,1,2,3; j 0,1,2,3
P31j P02j , j 0,1,2,3
P21j , P31j P02j , P12j , j 0,1,2,3
P21j P31j
2 2
0 j 1j
P P
2024
, j 0,1,2,3
Компьютерная графика
ЮФУ
Демяненко Я.М.
33

34. Бикубическая поверхность Безье: пример

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
34

35. NURBS – поверхности

2024
Компьютерная графика
ЮФУ
Демяненко Я.М.
35