Интерактивная компьютерная графика

1. (Сплайны)

Часть 8-2
(Сплайны)

2. Определения (нестрогое определение)

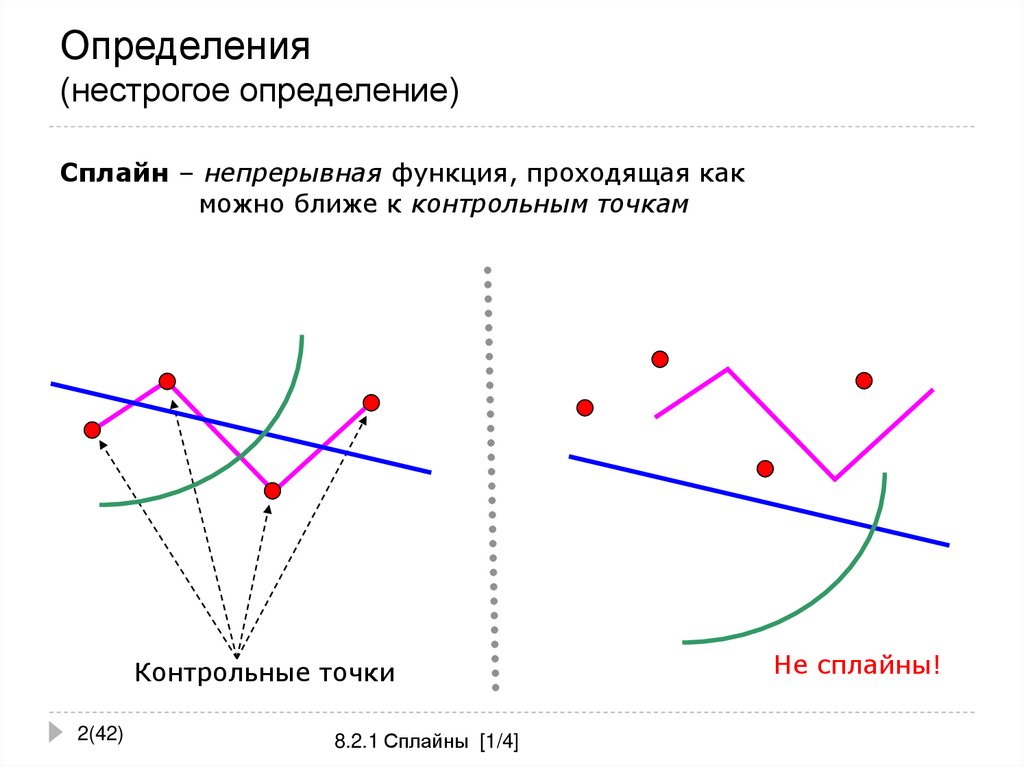
Сплайн – непрерывная функция, проходящая как
можно ближе к контрольным точкам
Контрольные точки
2(42)
8.2.1 Сплайны [1/4]
Не сплайны!

3. Определения (математические определения)

Сплайн – функция,
область определения которой разбита на подобласти,
на каждой из которых сплайн совпадает
с некоторым алгебраическим многочленом (полиномом)
Степень сплайна – максимальная степень использованных полиномов
Гладкость сплайна – максимальный порядок непрерывной
производной
Дефект сплайна – разность между степенью сплайна
и его гладкостью
Пример сплайна: ломаная (кусочно-линейная функция)
Производная сплайна: кусочно-постоянная функция
Степень сплайна:
1
Гладкость сплайна:
0
Дефект сплайна:
1
3(42)
8.2.1 Сплайны [2/4]

4. Виды сплайнов

По близости к контрольным точкам (КТ):
• Интерполяционные (обязаны проходить через КТ)
• Сглаживающие (не обязаны проходить через КТ)
По учету КТ при расчете коэффициентов сплайна:
• Локальные (коэффициенты рассчитываются через соседние КТ)
• Глобальные (коэффициенты рассчитываются через все КТ)
По типу производной:
• Рациональные (с разрывной производной)
• Нерациональные (с непрерывной 1ой, 2ой,... производной)
По типу используемых базисных функций:
• Полиномиальные (лагранжевые, эрмитовые,…)
• Неполиномиальные (логарифмические, тригонометрические,…)
По мерности пространства:
• Одномерные (кривые)
• Двумерные (поверхности)
4(42)
8.2.1 Сплайны [3/4]

5. Виды сплайнов

Контрольные точки:
( f – неизвестная функция)
f xi fi , i 1, n
hi xi 1 xi ,
i 1, n 1
Общий вид сплайна: P x
m
q ( x )
i 1
i
i
P xi fi
Условие для интерполяционного сплайна:
n
Условие для сглаживающего сплайна:
(методом Наименьших квадратов)
P x f
i 1
i
i
Задача сглаживания – построение достаточно гладкой функции,
значения которой в КТ максимально близки к
5(42)
8.2.1 Сплайны [4/4]
2
min
fi

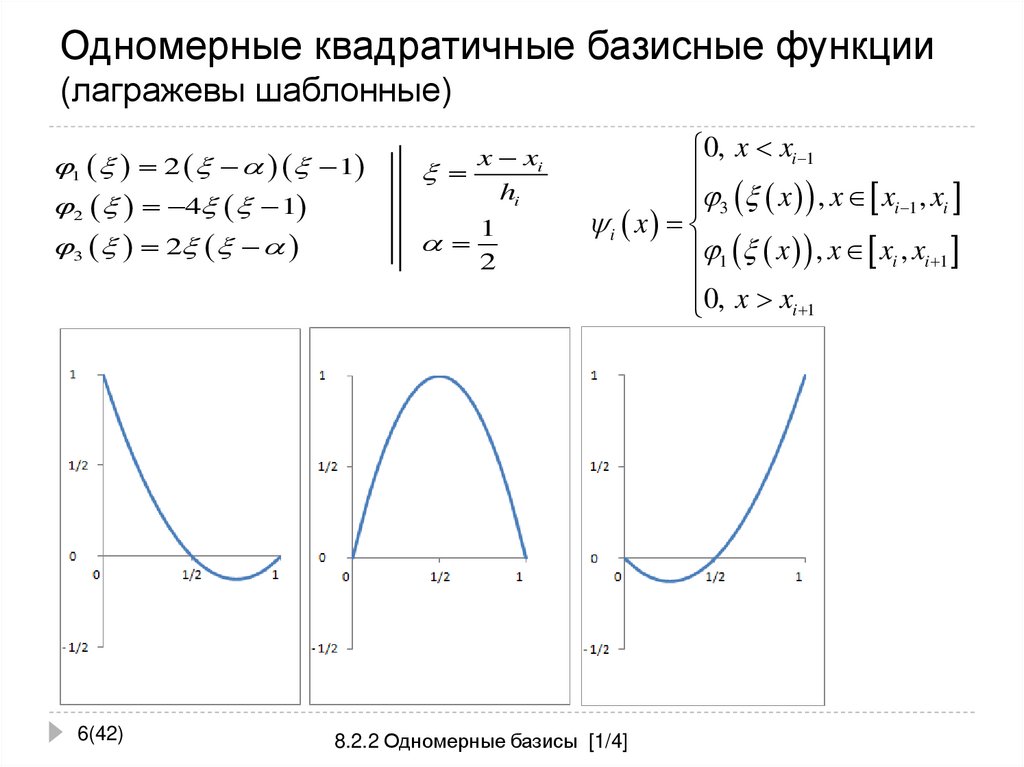
6. Одномерные квадратичные базисные функции (лагражевы шаблонные)

1 2 1
2 4 1
x xi
hi
3 2
6(42)
1
2
0, x xi 1
3 x , x xi 1 , xi
i x
1 x , x xi , xi 1
0, x xi 1
8.2.2 Одномерные базисы [1/4]

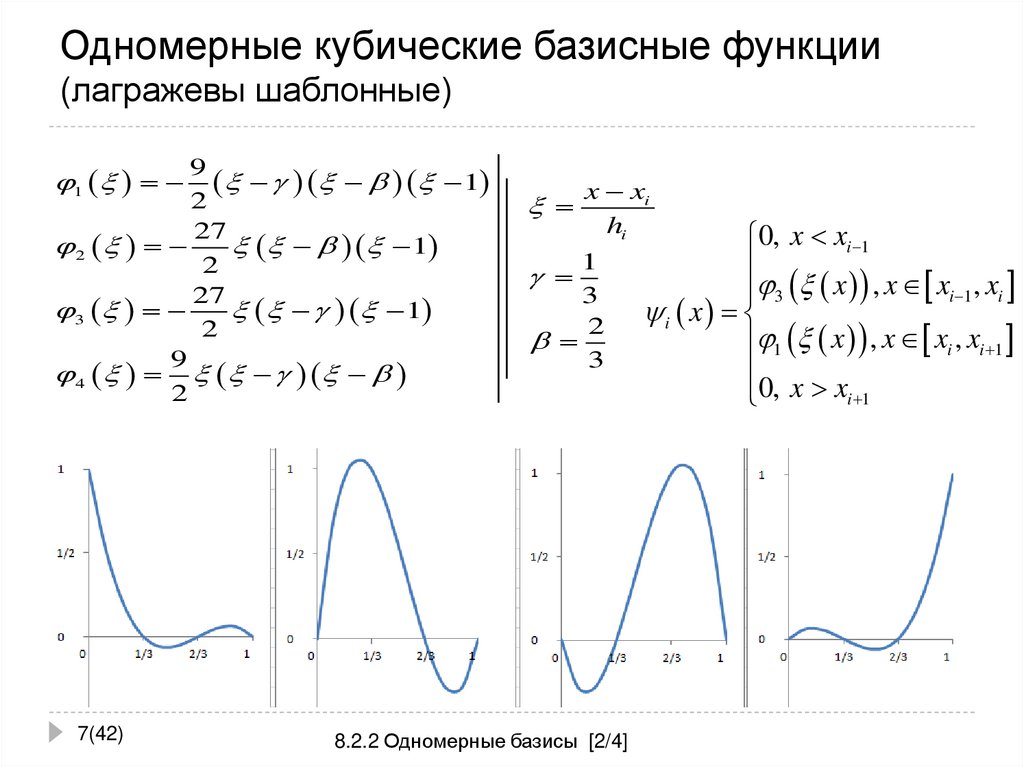
7. Одномерные кубические базисные функции (лагражевы шаблонные)

9
1
2
27
2
1
2
27
3
1
2
9
4
2
1
7(42)
x xi
hi
1
3
2
3
8.2.2 Одномерные базисы [2/4]
0, x xi 1
3 x , x xi 1 , xi
i x
1 x , x xi , xi 1
0, x xi 1

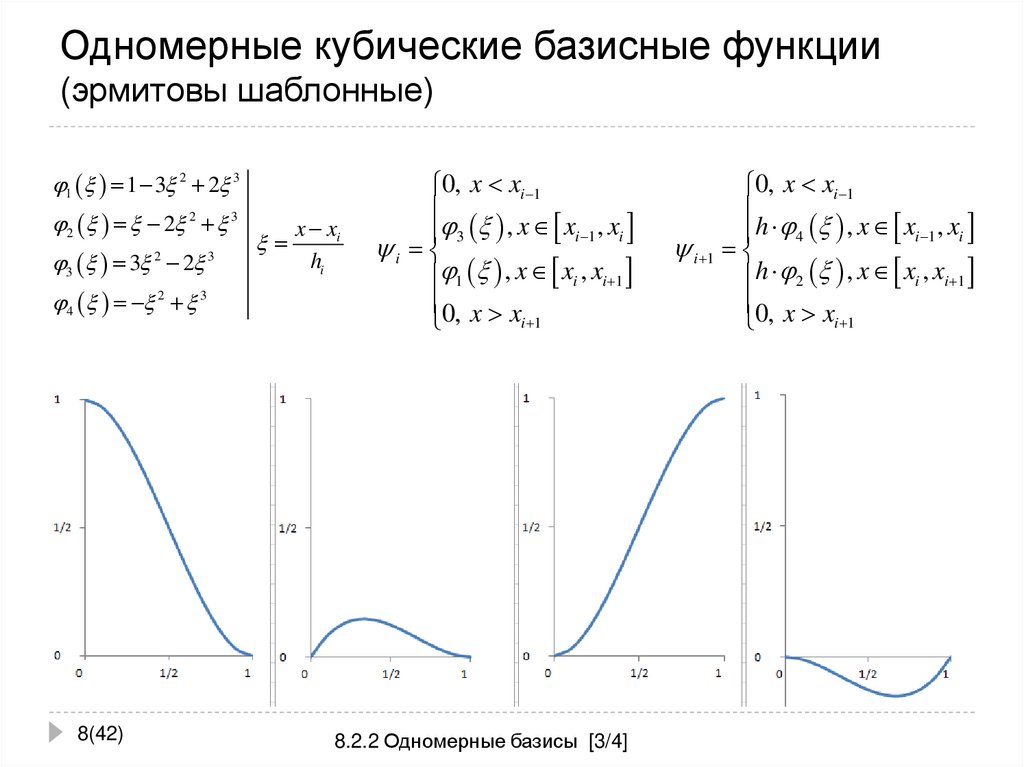
8. Одномерные кубические базисные функции (эрмитовы шаблонные)

1 1 3 2 2 3
2 2 2 3
3 3 2 2 3
4 2 3
8(42)
x xi
hi
0, x xi 1
3 , x xi 1 , xi
i
1 , x xi , xi 1
0, x x
i 1
8.2.2 Одномерные базисы [3/4]
0, x xi 1
h 4 , x xi 1 , xi
i 1
h 2 , x xi , xi 1
0, x x
i 1

9. Интерполяционный полином Лагранжа

Степени n:
x xj
L x fi
i 1
j i xi x j
Степени 1:
L x Pi1 x ,
n
n
n 1
1
i 1
Степени 2:
n 1
L x Pi x ,
2
2
i 1
Степени 3:
n 1
L x Pi x ,
3
3
i 1
9(42)
a x bi , x xi , xi 1
Pi1 x i
0, иначе
2
ai x bi x ci , x xi , xi 1
Pi x
0, иначе
2
3
2
ai x bi x ci x di , x xi , xi 1
Pi x
0, иначе
3
8.2.2 Одномерные базисы [4/4]

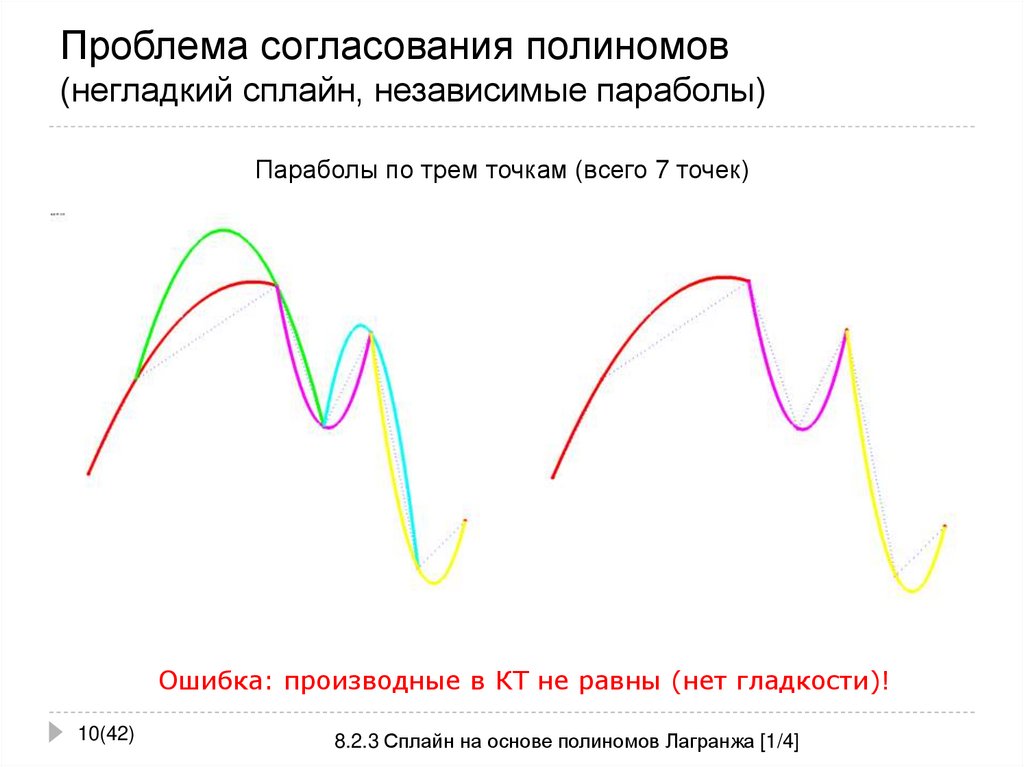
10. Проблема согласования полиномов (негладкий сплайн, независимые параболы)

Параболы по трем точкам (всего 7 точек)
Ошибка: производные в КТ не равны (нет гладкости)!
10(42)
8.2.3 Сплайн на основе полиномов Лагранжа [1/4]

11. Линейный сплайн с полиномами Лагранжа (формулы)

P x
n 1
Pi1 x , где Pi1 x ai x bi , x xi , xi 1
i 1
Pi x
xi
hi
xi 1
Система для определения
коэффициентов сплайна
ai
1
fi 1 fi
hi
bi fi ai xi
Pi xi fi
Pi xi 1 fi 1
11(42)
8.2.3 Сплайн на основе полиномов Лагранжа [2/4]

12. Квадратичный сплайн с полиномами Лагранжа (формулы)

P x
n 1
Pi 2 x , где Pi 2 x ai x 2 bi x ci , x xi , xi 1
i 1
a1
Pi x
xi
hi
1
1 '
f
f
f1
2
1
h12
h1
b1 f1' 2a1 x1
xi 1
c1 f1 f1' x1 a1 x12
f1'
f f
f
x1 2 1
x
h1
Система для определения
коэффициентов сплайна
Pi 2 xi fi
2
Pi xi 1 fi 1
2
Pi 21
Pi
x xi x xi
12(42)
ai
1
1
f
f
i
i 1
i
hi2
hi
bi i 2ai xi
i 2ai 1 xi bi 1
ci fi i xi ai xi2
8.2.3 Сплайн на основе полиномов Лагранжа [3/4]

13. Кубический сплайн с полиномами Лагранжа (формулы)

P x
n 1
Pi 3 x , где Pi 3 x ai x3 bi x 2 ci x di , x xi , xi 1
i 1
a1
Pi x
xi
hi
xi 1
Система для определения
коэффициентов сплайна
Pi 3 xi f i
3
Pi xi 1 f i 1
3
3
Pi x Pi 1 x
i
x i
x
2 3
2 3
P
Pi 1
i
x
x
2 i
x 2 i
x
13(42)
1
1 ' 1 ''
f
f
f
f1
2
1
3
2 1
h1
h1
2h1
1 ''
f1 3a1 x1
2
c1 f1' 2b1 x1 3a1 x12
b1
f1'
f f
f
x1 2 1
x
h1
2 f
f 2 x1 0
x
''
1
d1 f1 c1 x1 b1 x12 a1 x13
ai
1
1
1
f
f
i
i 1
i
i
hi3
hi2
hi
bi i 3ai xi
ci i 2bi xi 3ai xi2
i 3ai 1 xi2 2bi 1 xi ci 1
i 3ai 1 xi bi 1
di fi ci xi bi xi2 ai xi3
8.2.3 Сплайн на основе полиномов Лагранжа [4/4]

14. Кубический сплайн с полиномами Эрмита (интерполяционный сплайн)

n
n
i 1
i 1
P x fi 2i -1 ( x) fi ' 2i ( x)
f i ' – значения производных квадратичного полинома Лагранжа для xi 1 , xi , xi 1
dL2i x f i 1
x xi x xi 1 f x xi 1 x xi 1 f x xi x xi 1
xi 1 xi xi 1 xi 1 i xi xi 1 xi xi 1 i 1 xi 1 xi xi 1 xi 1
fi ' x
14(42)
f
xi dL2i xi
x
f
x1 dL22 x1
x
f
f n' x xn dL2n 1 xn
x
f1' x
8.2.4 Сплайн на основе полиномов Эрмита [1/3]

15. Кубический сплайн с полиномами Эрмита (сглаживающий сплайн)

x1 , xn
k
i
i 1
область подразбивается на конечные элементы
с эрмитовыми базисными функциями
n
P x f
Условие для сглаживающего сплайна:
i 1
i
i
2
min
Функционал минимизации для расчета коэффициентов:
A j x j
n
T
j 1
2
T
T
2k
F q = j qi i x j f j q Aq 2q b c
j=1
i 1
n
b j x j f j
n
j 1
n
c j f j2
j 1
Функционал в случае неединственности:
F p = j P( x j ) f j
k
j=1
15(42)
2
2
n
d 2 P( x)
dP( x)
( x)
dx
dx ( x)
2
dx
dx
x1
x1
xn
2
x
8.2.4 Сплайн на основе полиномов Эрмита [2/3]
x
j

16. Кубический сплайн с полиномами Эрмита (сглаживающий сплайн)

Эквивалентное матричное уравнение:
Aq b
Матрица A и вектор b собираются
i
i
из стандартных локальных матриц Aˆ и векторов bˆ
конечного элемента i :
d ˆ d ˆ m
aˆlm j ˆ l x j ˆ m x j x l
dx
dx dx
j 1
xi
xi 1
n
xi 1
xi
d 2 ˆ l d 2 ˆ m
x 2
dx
2
dx dx
bˆl j ˆ l x j f j
n
j 1
Расчет значения сплайна в любой точке:
2k
P x qi i x
i 1
16(42)
8.2.4 Сплайн на основе полиномов Эрмита [3/3]
l , m 1, 4

17. Кривая Безье (Bezier Curve)

Кривая Безье – это параметрическая кривая вида:
n 1
B t Pi bi ,n 1 t , t 0,1
i 0
Pi xi , fi – вектор i-й контрольной точки
bi , j – базисные функции кривой Безье (полиномы Бернштейна):
bi , j t C ij t i 1 t
C ij
j i
j!
– число сочетаний из j по i
i ! j i !
Расчет значения сплайна в точке (x,y) x t B t
x
для конкретного значения параметра t:
y t By t
17(42)
8.2.5 Кривая Безье [1/6]

18. Кривая Безье (2 Контрольных Точки)

Кривая представляет собою отрезок P0 , P1
Q B ti – точка на отрезке P0 , P1
18(42)
8.2.5 Кривая Безье [2/6]

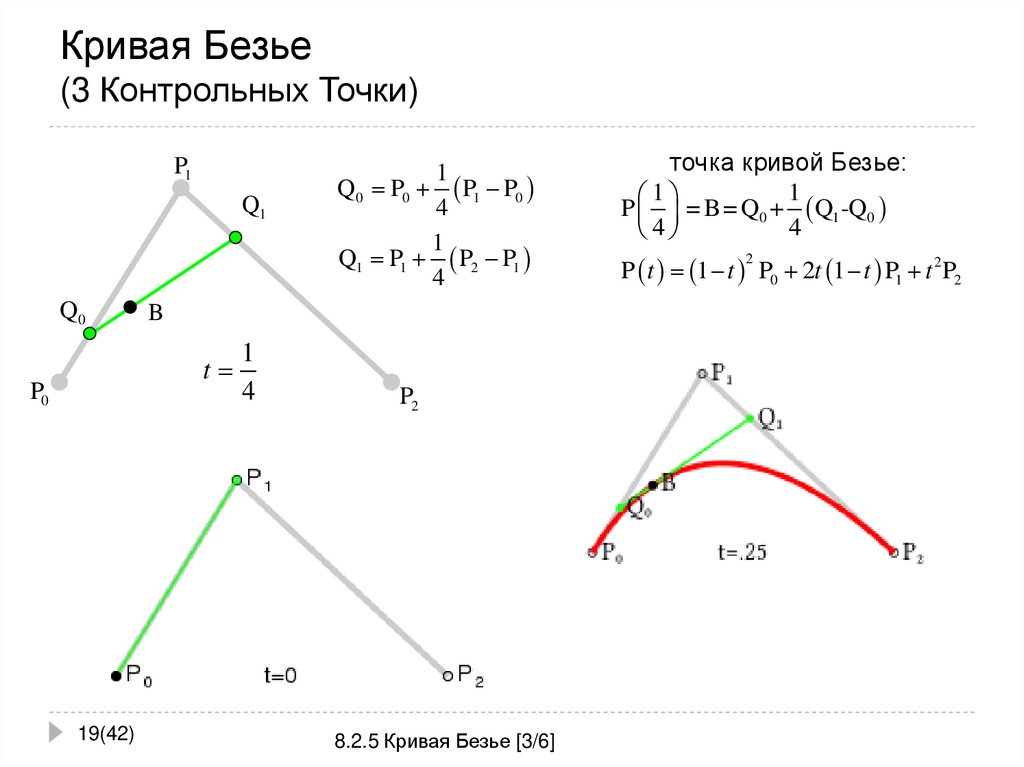
19. Кривая Безье (3 Контрольных Точки)

P1
Q1
Q0
B
t
P0
19(42)
1
Q0 P0 P1 P0
4
1
Q1 P1 P2 P1
4
1
4
P2
8.2.5 Кривая Безье [3/6]
точка кривой Безье:
1
1
P = B= Q0 + Q1 -Q0
4
4
P t 1 t P0 2t 1 t P1 t 2 P2
2

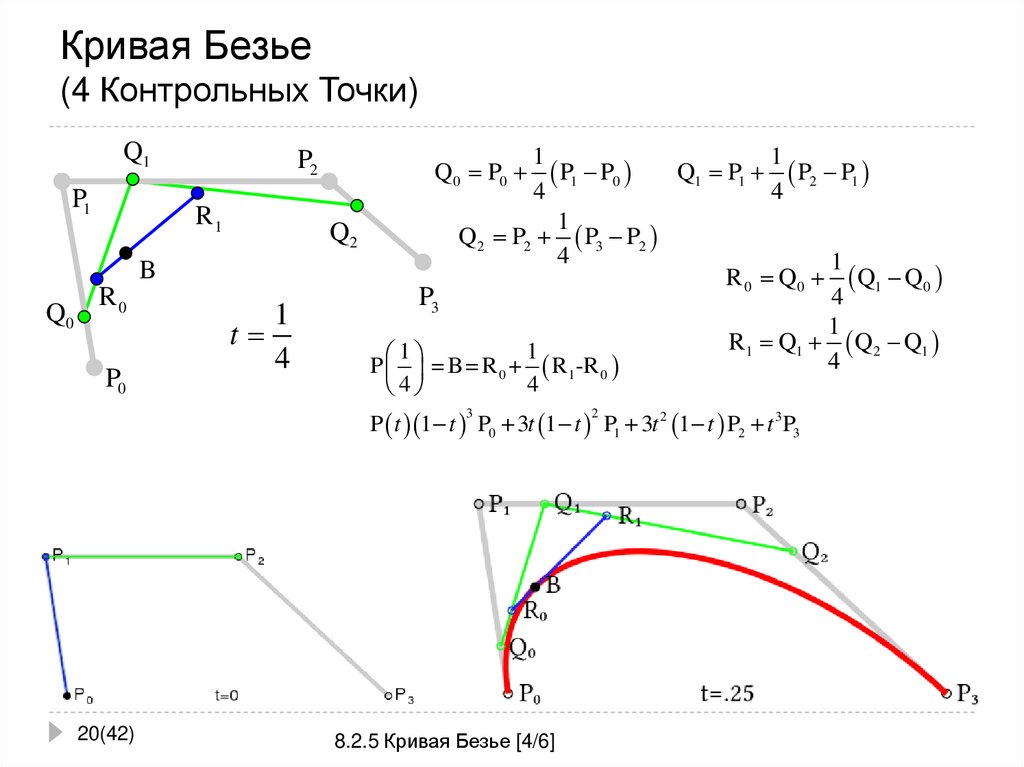
20. Кривая Безье (4 Контрольных Точки)

Q1
P1
P2
R1
B
Q0
R0
P0
t
1
4
1
1
P1 P0 Q1 P1 P2 P1
4
4
1
Q2
Q 2 P2 P3 P2
4
1
R 0 Q0 Q1 Q0
4
P3
1
R
Q
Q2 Q1
1
1
1
1
4
P = B= R 0 + R1 -R 0
Q0 P0
4
4
P t 1 t P0 3t 1 t P1 3t 2 1 t P2 t 3P3
3
20(42)
8.2.5 Кривая Безье [4/6]
2

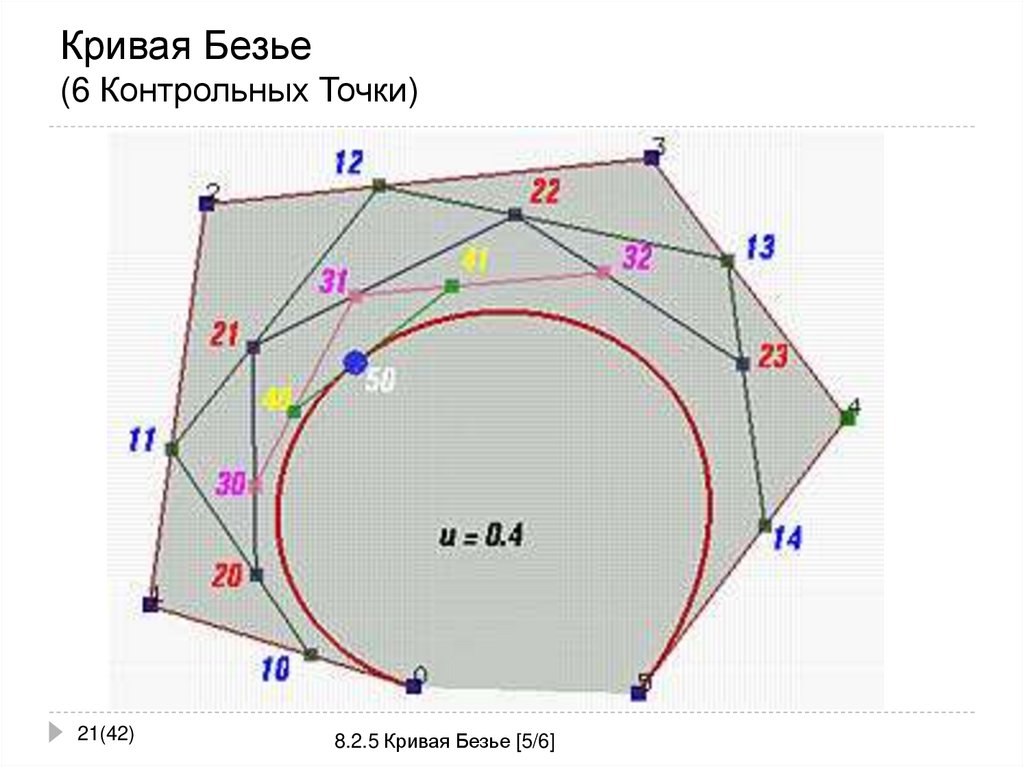
21. Кривая Безье (6 Контрольных Точки)

21(42)
8.2.5 Кривая Безье [5/6]

22. Кривая Безье (некоторые свойства)

соединяет начальную и конечную КТ,
но нельзя получить окружность
изменение координат хотя бы одной из точек
ведет к изменению формы всей кривой (глобальность)
всегда располагается внутри фигуры (выпуклой оболочки),
образованной линиями, соединяющими контрольные точки
симметрична, то есть обмен местами между начальной и конечной КТ
(изменение направления траектории) не влияет на форму кривой
степень кривой всегда на одну ступень ниже числа КТ
(например, при трех контрольных точках форма кривой – парабола)
22(42)
8.2.5 Кривая Безье [6/6]

23. B-сплайн (определение)

B-сплайн – это сплайн-функция,
имеющая наименьший носитель для заданных:
• степени
• гладкости
• разбиения области определения
B-сплайн – это «базисный сплайн»
Теорема: любой сплайн с заданной степенью, гладкостью и областью
может быть представлен как линейная комбинация B-сплайнов
той же степени и гладкости на той же области определения
23(42)
8.2.6 B-сплайн [1/4]

24. B-сплайн (определение)

B-сплайн – это параметрическая кривая, задаваемая выражением:
n 1
P t Pi Bi , p t ,
i 0
t T tmin , tmax специальный вектор узлов (не КТ !)
p 2, n 1 – степень сплайна степень полинома 1
Базисные функции рассчитываются
по рекуррентным формулам Кокса-де Бура:
1, t ti , ti 1
Bi ,0 t
0, иначе
Bi ,k t
24(42)
t ti Bi ,k 1 t ti k t Bi 1,k 1 t
ti k 1 ti
ti k ti 1
8.2.6 B-сплайн [2/4]

25. B-сплайн (задание вектора узлов)

Открытый B-сплайн:
T 0, 1, 2,..., n p 1
T T1 T 2 T 3
Закрытый B-сплайн:
T11 p 0, 0,..., 0
T1 2 n p 1, 2,..., n p
T1 3 p n p 1,..., n p 1
T 1, 2, 3,..., n 2 p 1
Замкнутый B-сплайн:
f f1 , f 2 ,..., f n f1 , f 2 ,..., f p 1
n 1
p 1
i 0
i 0
P t Pi Bi , p 1 t Pi Bi n , p 1 t
25(42)
8.2.6 B-сплайн [3/4]

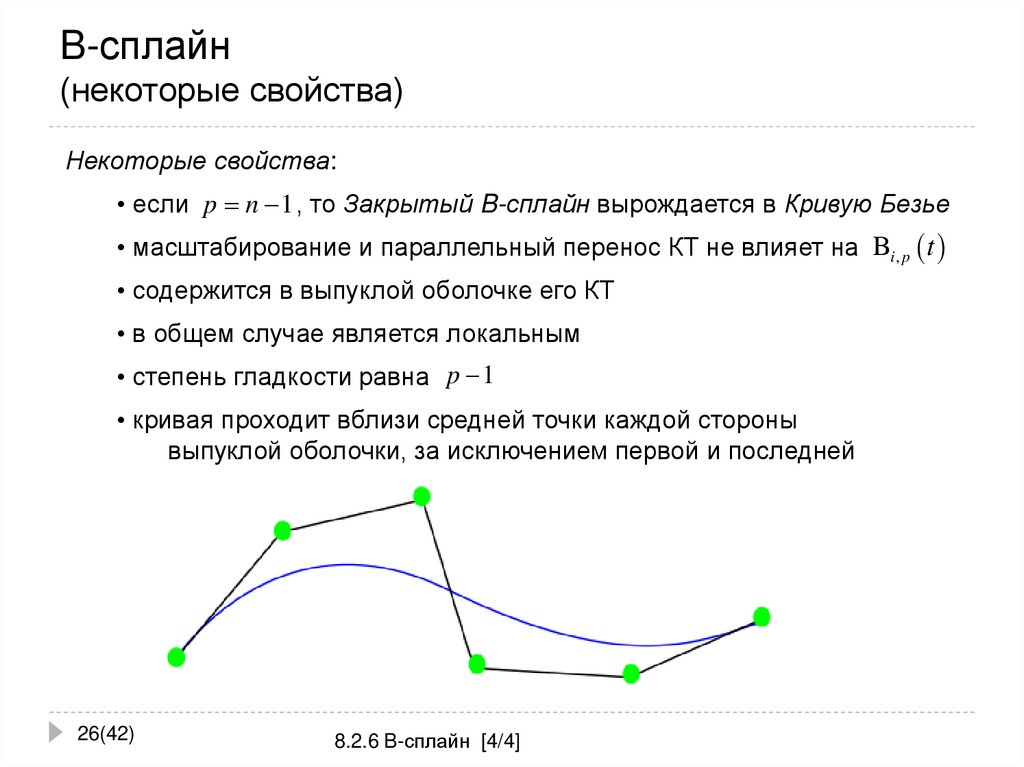
26. B-сплайн (некоторые свойства)

Некоторые свойства:
• если p n 1 , то Закрытый B-сплайн вырождается в Кривую Безье
• масштабирование и параллельный перенос КТ не влияет на Bi , p t
• содержится в выпуклой оболочке его КТ
• в общем случае является локальным
• степень гладкости равна p 1
• кривая проходит вблизи средней точки каждой стороны
выпуклой оболочки, за исключением первой и последней
26(42)
8.2.6 B-сплайн [4/4]

27. NURBS-сплайн (Non-Uniform Rational B-Spline)

NURBS – неоднородный рациональный B-сплайн
Рациональный В-сплайн – это проекция (обобщение)
нерационального (полиномиального) В-сплайна,
определенного в четырехмерном (4D)
однородном координатном пространстве,
на трехмерное (3D) физическое пространство
x y z
x
,
y
,
z
,
, , x ', y ', z '
Если узлы равноудалены друг от друга,
то B-сплайн является однородным,
в противном случае - неоднородный
27(42)
8.2.7 NURBS-сплайн [1/2]

28. NURBS-сплайн (Non-Uniform Rational B-Spline)

n -1
B t
'
P
i i Bi, p t
i =0
n -1
B t
i
i =0
i, p
n -1
Pi' R i , p t
i =0
Pi' – вершины полигона в 3D
R i , p t – базисные функции,
i – веса контрольных точек
28(42)
8.2.7 NURBS-сплайн [2/2]
n -1
R t 1
i, p
i =0

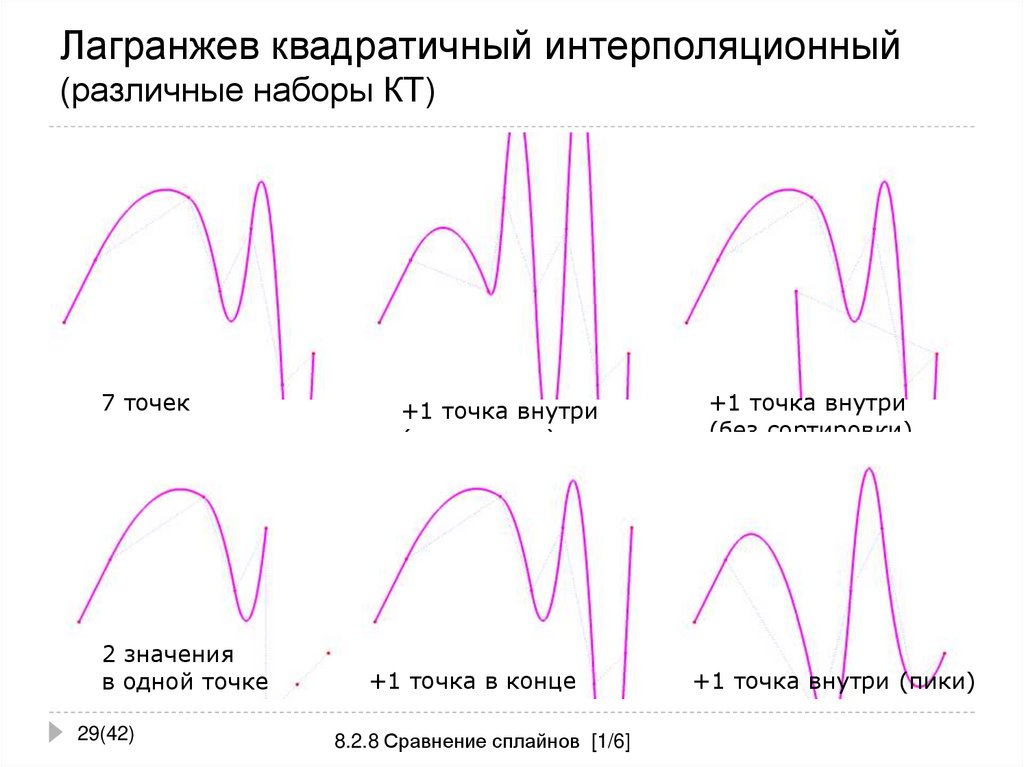
29. Лагранжев квадратичный интерполяционный (различные наборы КТ)

7 точек
2 значения
в одной точке
29(42)
+1 точка внутри
(сортировка)
+1 точка в конце
8.2.8 Сравнение сплайнов [1/6]
+1 точка внутри
(без сортировки)
+1 точка внутри (пики)

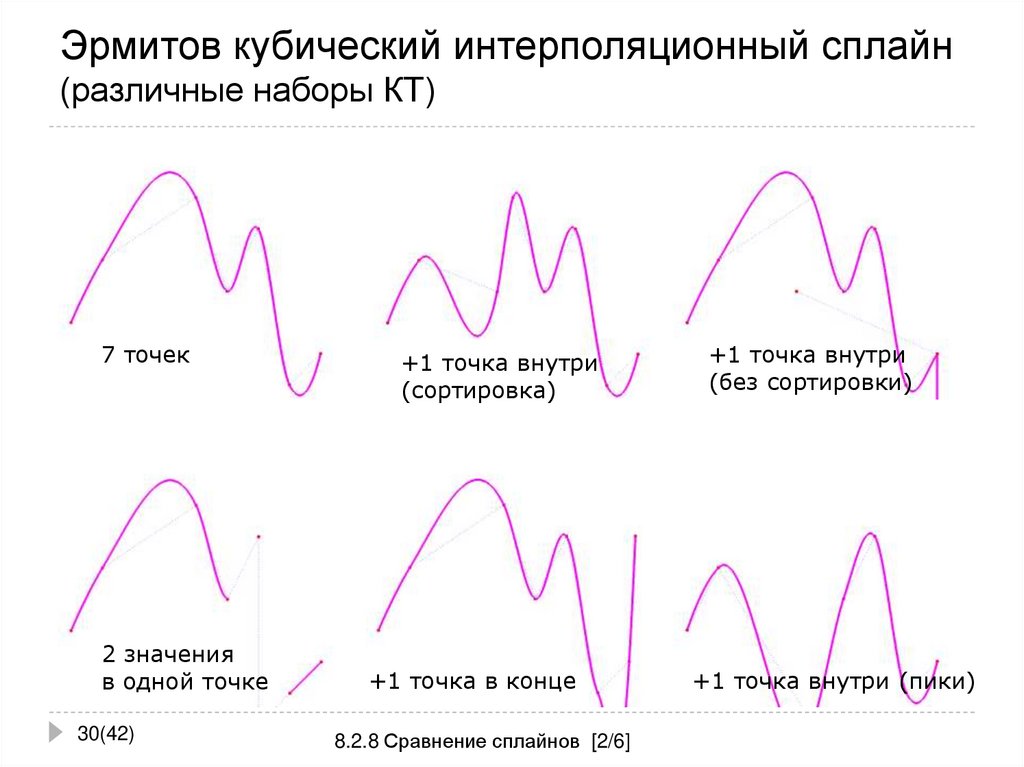
30. Эрмитов кубический интерполяционный сплайн (различные наборы КТ)

7 точек
2 значения
в одной точке
30(42)
+1 точка внутри
(сортировка)
+1 точка в конце
8.2.8 Сравнение сплайнов [2/6]
+1 точка внутри
(без сортировки)
+1 точка внутри (пики)

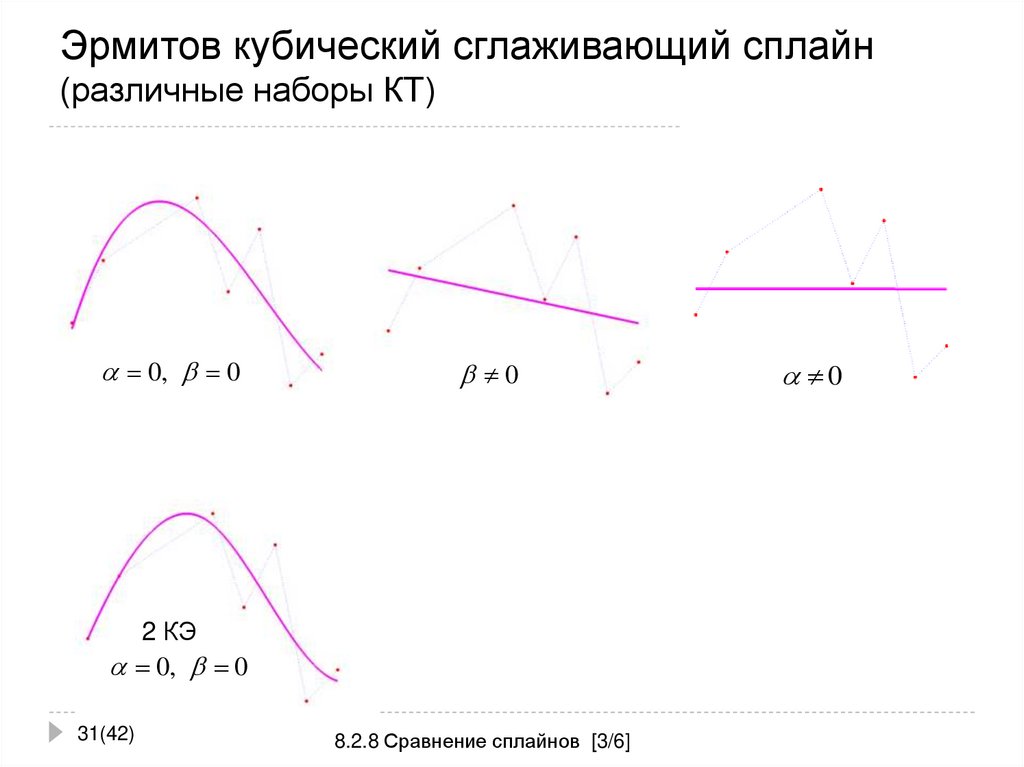
31. Эрмитов кубический сглаживающий сплайн (различные наборы КТ)

0, 0
0
2 КЭ
0, 0
31(42)
8.2.8 Сравнение сплайнов [3/6]
0

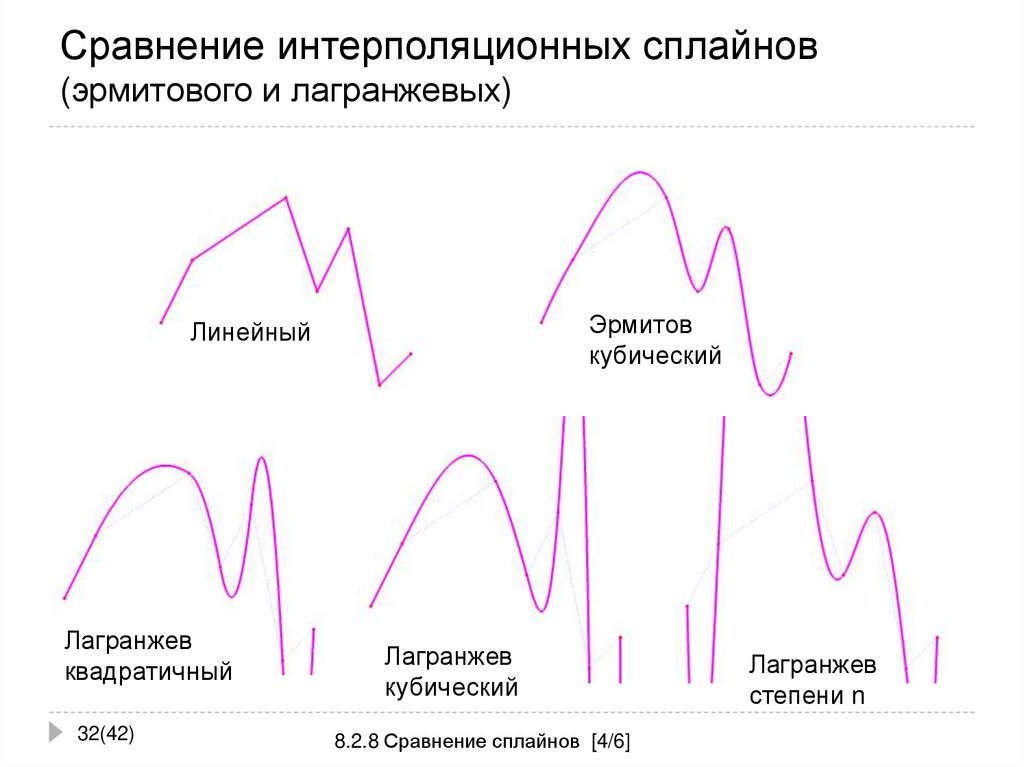
32. Сравнение интерполяционных сплайнов (эрмитового и лагранжевых)

Эрмитов
кубический
Линейный
Лагранжев
квадратичный
32(42)
Лагранжев
кубический
8.2.8 Сравнение сплайнов [4/6]
Лагранжев
степени n

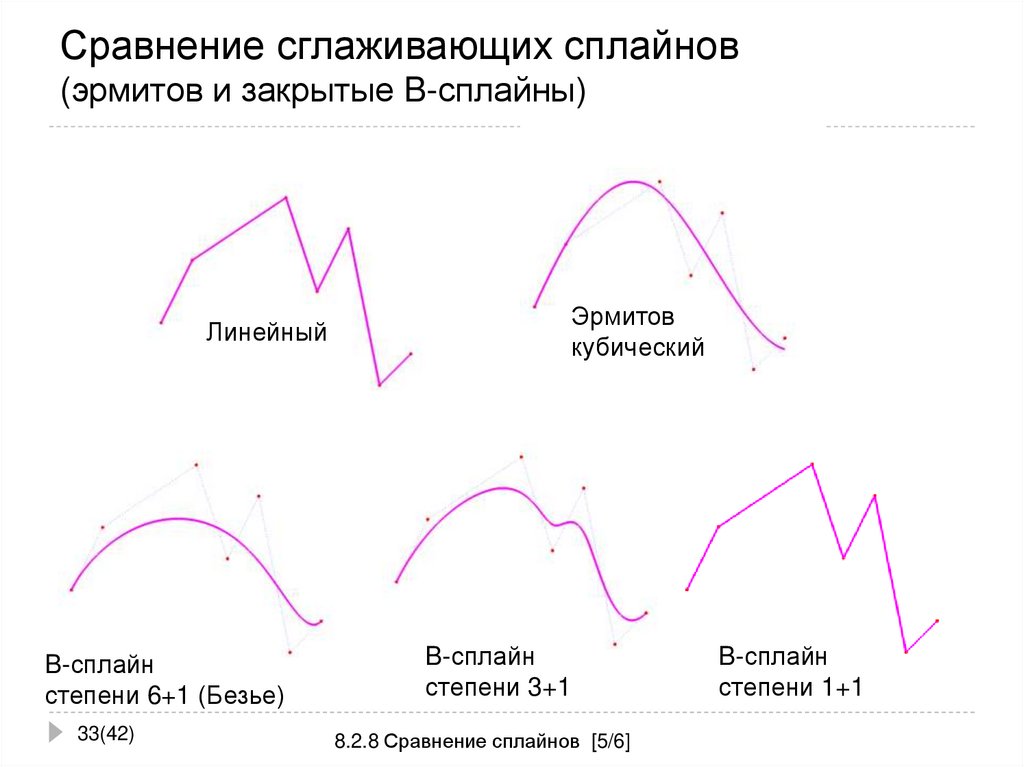
33. Сравнение сглаживающих сплайнов (эрмитов и закрытые B-сплайны)

Линейный
B-сплайн
степени 6+1 (Безье)
33(42)
Эрмитов
кубический
B-сплайн
степени 3+1
8.2.8 Сравнение сплайнов [5/6]
B-сплайн
степени 1+1

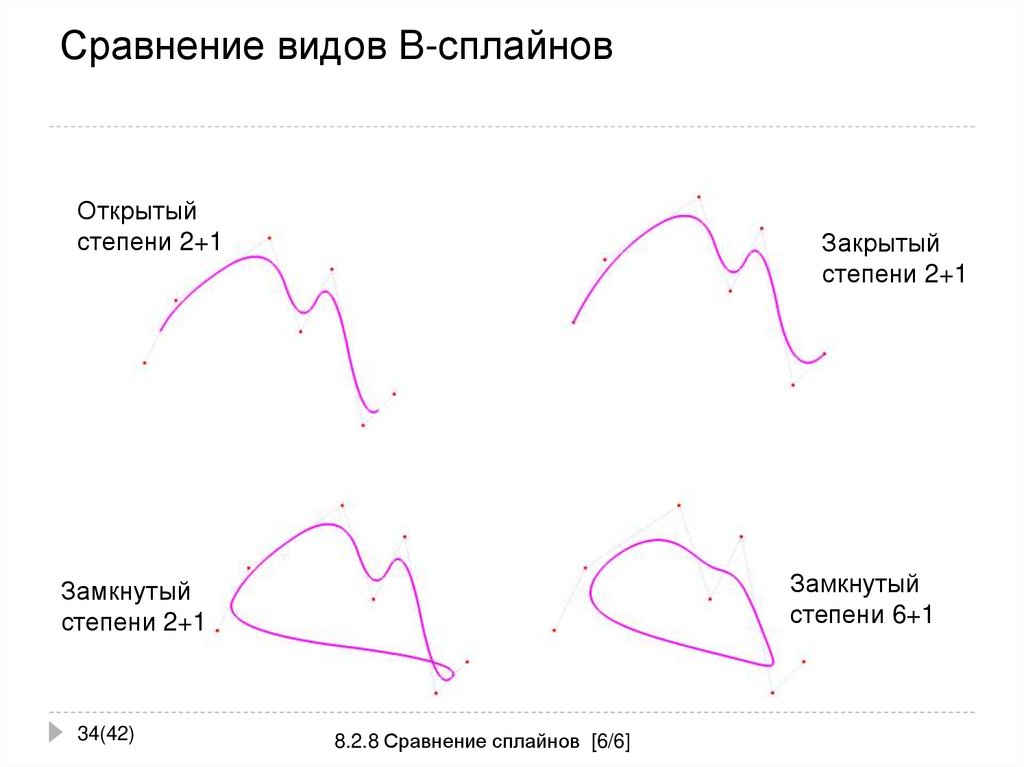
34. Сравнение видов B-сплайнов

Открытый
степени 2+1
Закрытый
степени 2+1
Замкнутый
степени 6+1
Замкнутый
степени 2+1
34(42)
8.2.8 Сравнение сплайнов [6/6]

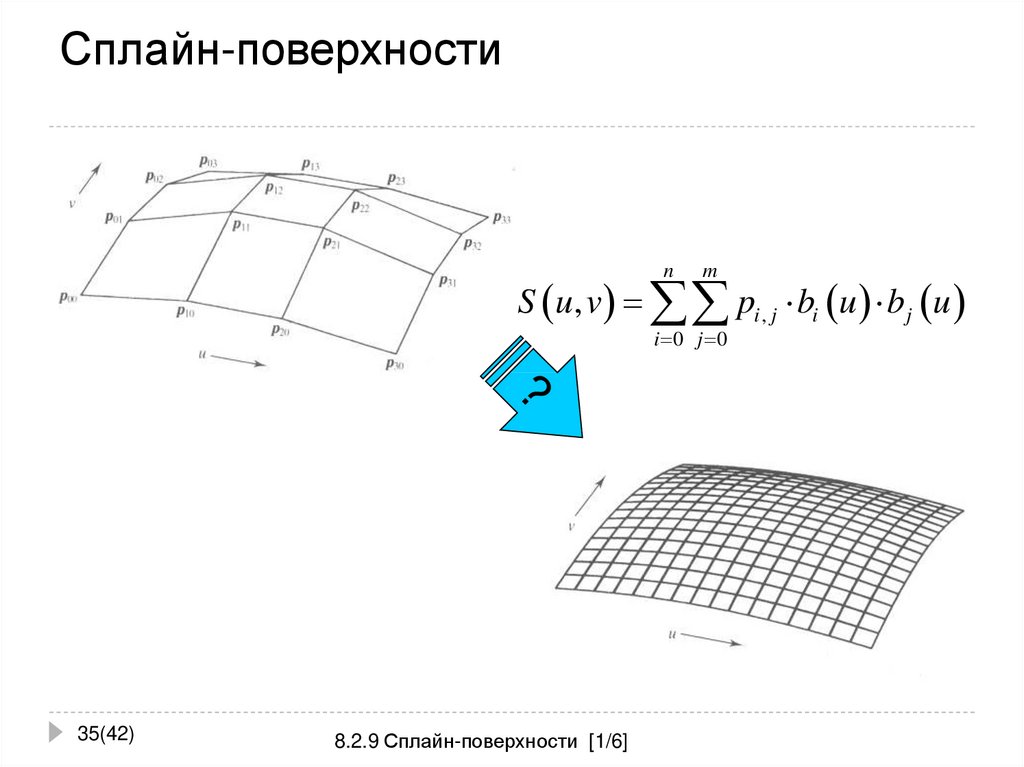
35. Сплайн-поверхности

n
m
S u, v pi , j bi u b j u
i 0 j 0
35(42)
8.2.9 Сплайн-поверхности [1/6]

36. Сплайн-поверхности (Безье и B-сплайн)

Pi , j (n m) контрольных точек (вершин сетки)
Поверхность Безье
порядка (n-1,m-1)
n 1 m 1
P u, v Pi , j Bi ,n 1 u B j ,m 1 v
i =0 j 0
Поверхность B-сплайна
порядка (p,q):
n 1 m 1
P u, v Pi , j Bi , p u B j ,q v
i =0 j 0
n 1 m 1
Поверхность NURBS
порядка (p,q):
P u, v
w
i =0 j 0
n 1 m 1
w
i =0 j 0
36(42)
P Bi , p u B j ,q v
i, j i, j
8.2.9 Сплайн-поверхности [2/6]
i, j
Bi , p u B j ,q v

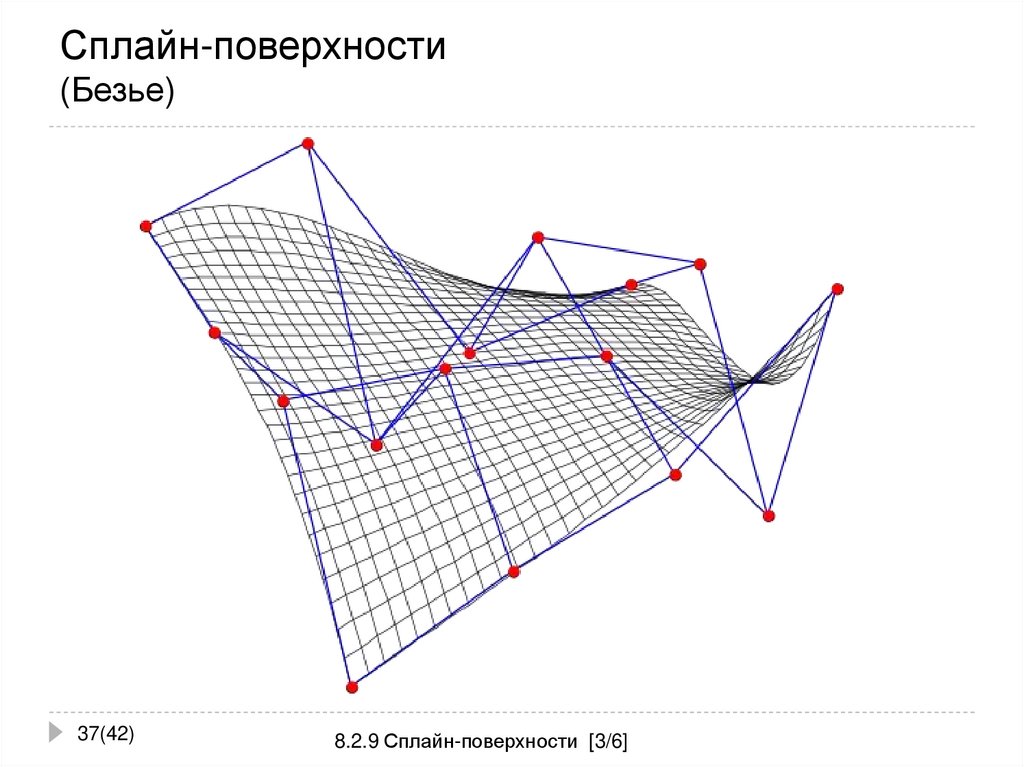
37. Сплайн-поверхности (Безье)

37(42)
8.2.9 Сплайн-поверхности [3/6]

38. Сплайн-поверхности (Безье)

38(42)
8.2.9 Сплайн-поверхности [4/6]

39. Сплайн-поверхности (сплайн Безье, чайник Юта)

39(42)
8.2.9 Сплайн-поверхности [5/6]

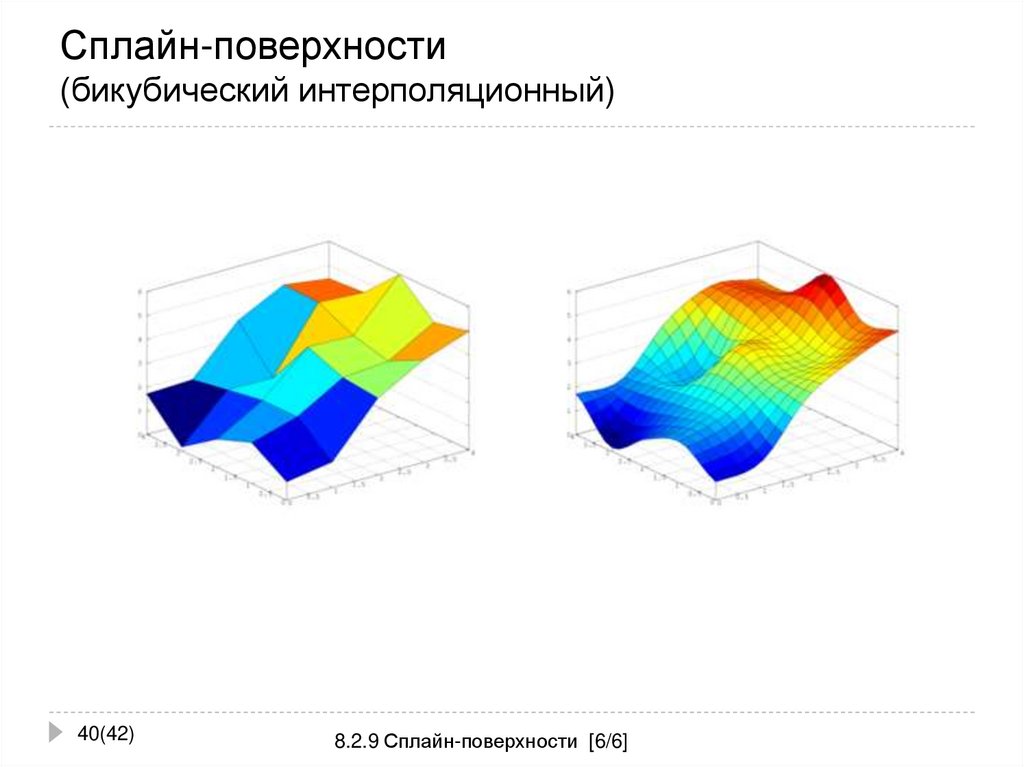
40. Сплайн-поверхности (бикубический интерполяционный)

40(42)
8.2.9 Сплайн-поверхности [6/6]

41. Поддержка в OpenGL (библиотека GLU)

gluNewNurbsRenderer ()
// создание объекта типа NURBS
gluDeleteNurbsRenderer (*) // создание объекта типа NURBS
gluNurbsProperty (*) // задание свойств
gluNurbsCallback() // проверка на ошибки и возврат значений
gluBeginSurface (*) // начало рисование поверхности
gluNurbsSurface (*) // передача контрольных точек, нормалей,….
gluEndSurface (*) // завершение рисования поверхности
gluBeginCurve (*) // начало рисование кривой
gluNurbsCurve (*) // передача контрольных точек, нормалей,….
gluEndCurve (*) // завершение рисования кривой
41(42)
8.2.10 Поддержка в OpenGL [1/2]

42. Поддержка в OpenGL (пример построения Безье с равномерным шагом)

parts = 20 * n;
gl.Map1(OpenGL.GL_MAP1_VERTEX_3, 0f, 1f, 3, n, ver3);
gl.Enable(OpenGL.GL_MAP1_VERTEX_3);
gl.MapGrid1(parts, 0f, 1f);
gl.EvalMesh1(OpenGL.GL_LINE, 0, parts);
gl.Disable(OpenGL.GL_MAP1_VERTEX_3);
42(42)
8.2.10 Поддержка в OpenGL [2/2]