Похожие презентации:
Теорема Менелая. 10 класс
1.
Теорема Менелая10 класс
2.
• Менела́й Александри́йскийдревнегреческий математик иастроном (ок. 100 г. н. э.). Автор
работ по сферической
тригонометрии: 6 книг о
вычислении хорд и 3 книги
«Сферики» (сохранились в
арабском переводе).
Тригонометрия у Менелая
отделена от геометрии и
астрономии. Арабские авторы
упоминают также о книге
Менелая по гидростатике.
3.
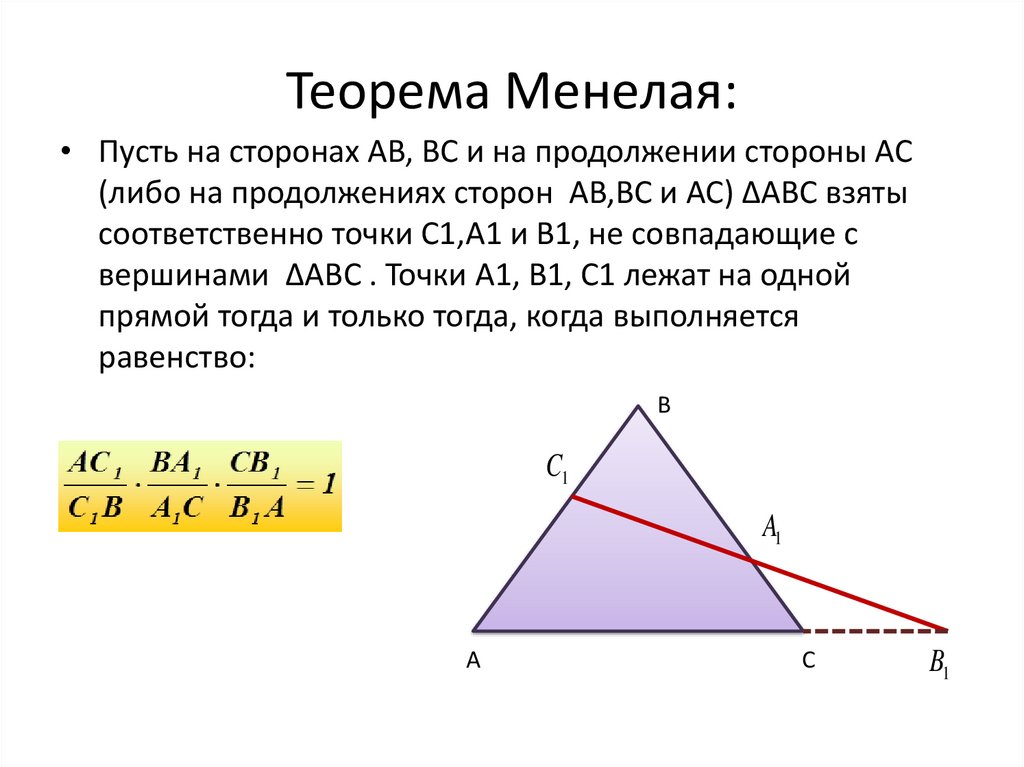
Теорема Менелая:• Пусть на сторонах AB, BC и на продолжении стороны AC
(либо на продолжениях сторон AB,BC и AC) ∆ABC взяты
соответственно точки C1,A1 и B1, не совпадающие с
вершинами ∆ABC . Точки A1, B1, C1 лежат на одной
прямой тогда и только тогда, когда выполняется
равенство:
В
C1
A1
А
С
B1
4.
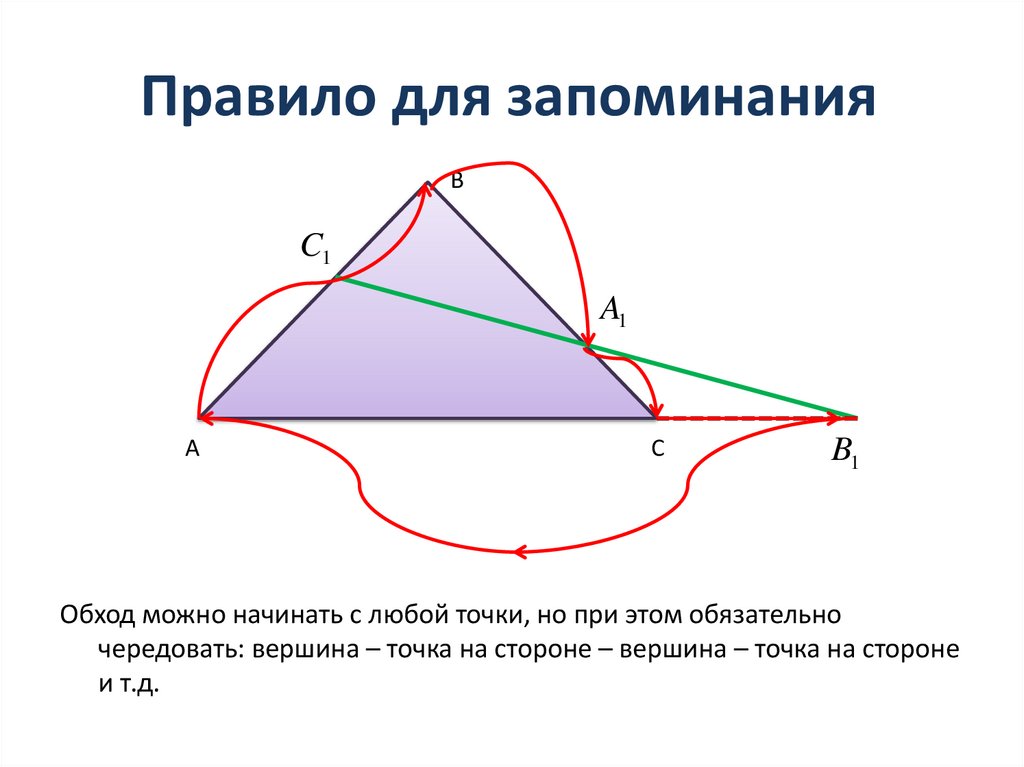
Правило для запоминанияВ
C1
A1
А
С
B1
Обход можно начинать с любой точки, но при этом обязательно
чередовать: вершина – точка на стороне – вершина – точка на стороне
и т.д.
5.
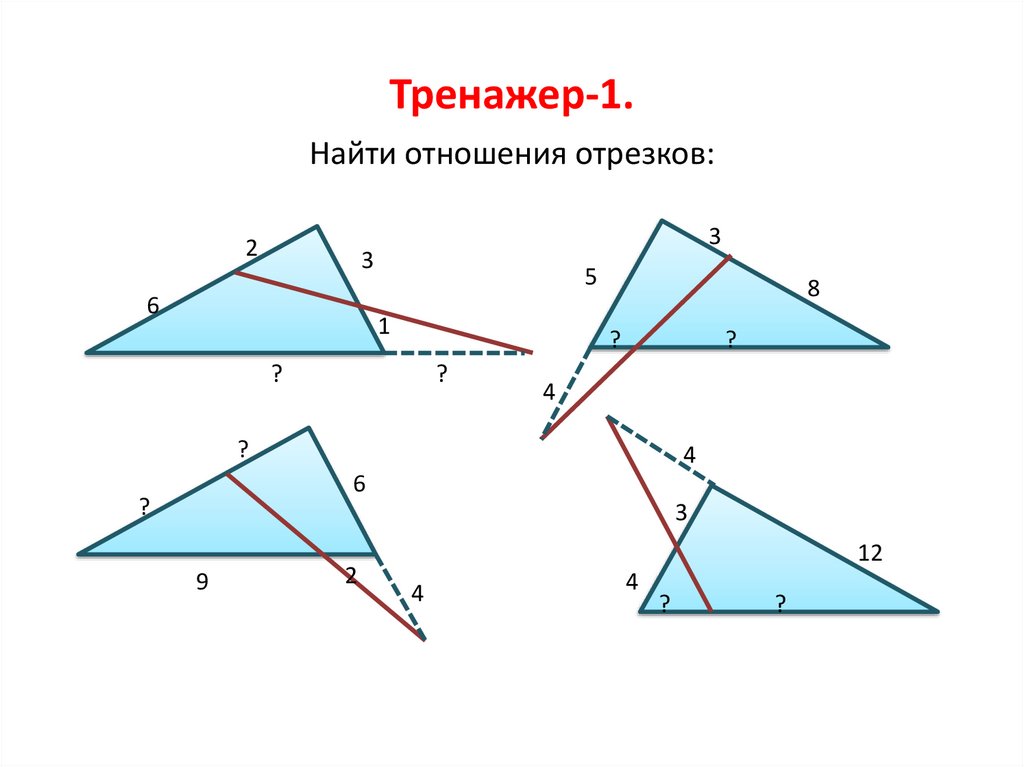
Тренажер-1.Найти отношения отрезков:
2
3
3
6
5
1
8
?
?
?
?
4
?
4
6
?
3
9
2
12
4
4
?
?
6.
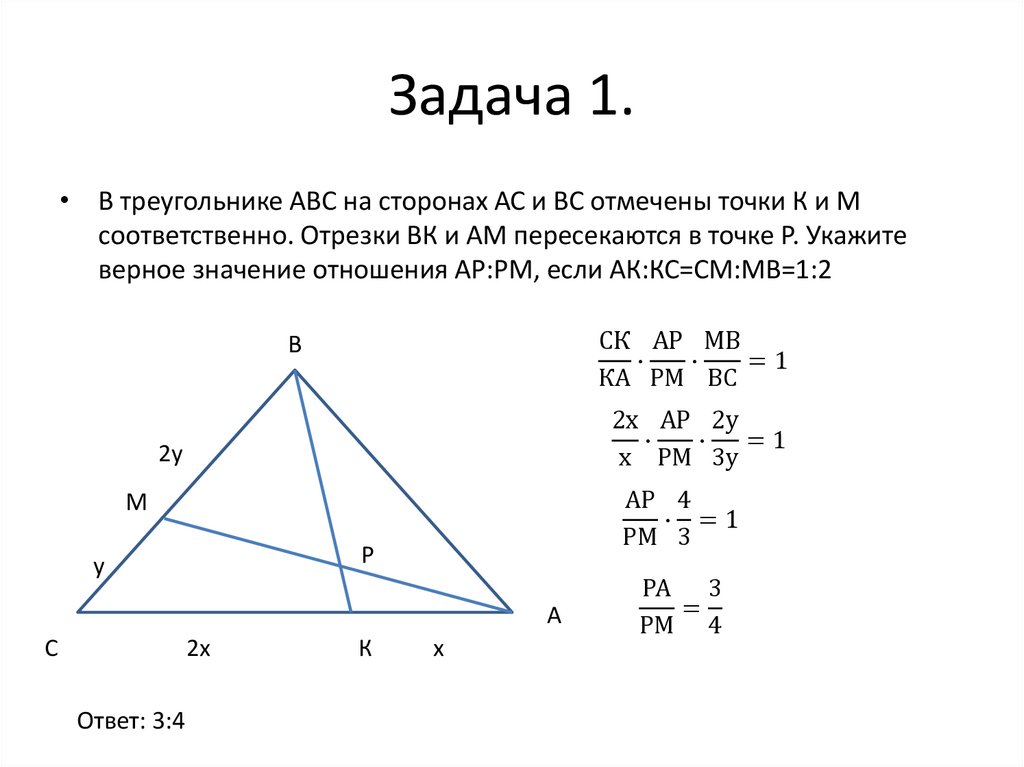
Задача 1.• В треугольнике АВС на сторонах АС и ВС отмечены точки К и М
соответственно. Отрезки ВК и АМ пересекаются в точке Р. Укажите
верное значение отношения АР:РМ, если АК:КС=СМ:МВ=1:2
СК АР МВ
∙
∙
=1
КА РМ ВС
В
2х АР 2у
∙
∙
=1
х РМ 3у
2у
АР 4
∙ =1
РМ 3
М
Р
у
А
С
2х
Ответ: 3:4
К
х
РА 3
=
РМ 4
7.
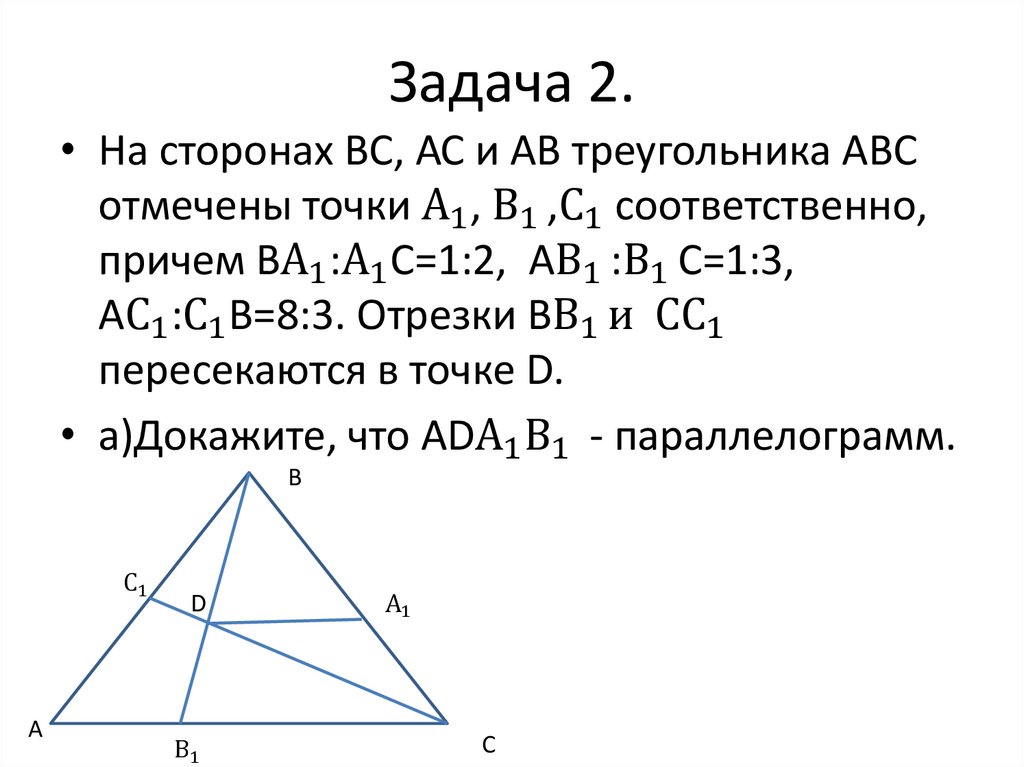
Задача 2.• На сторонах ВС, АС и АВ треугольника АВС
отмечены точки А1 , В1 ,С1 соответственно,
причем ВА1 :А1 С=1:2, АВ1 :В1 С=1:3,
АС1 :С1 В=8:3. Отрезки ВВ1 и СС1
пересекаются в точке D.
• а)Докажите, что АDА1 В1 - параллелограмм.
В
С1
А
D
В1
А1
С
8.
Использование теоремы Менелая встереометрических задачах.
M
F
B
K
O
A
D
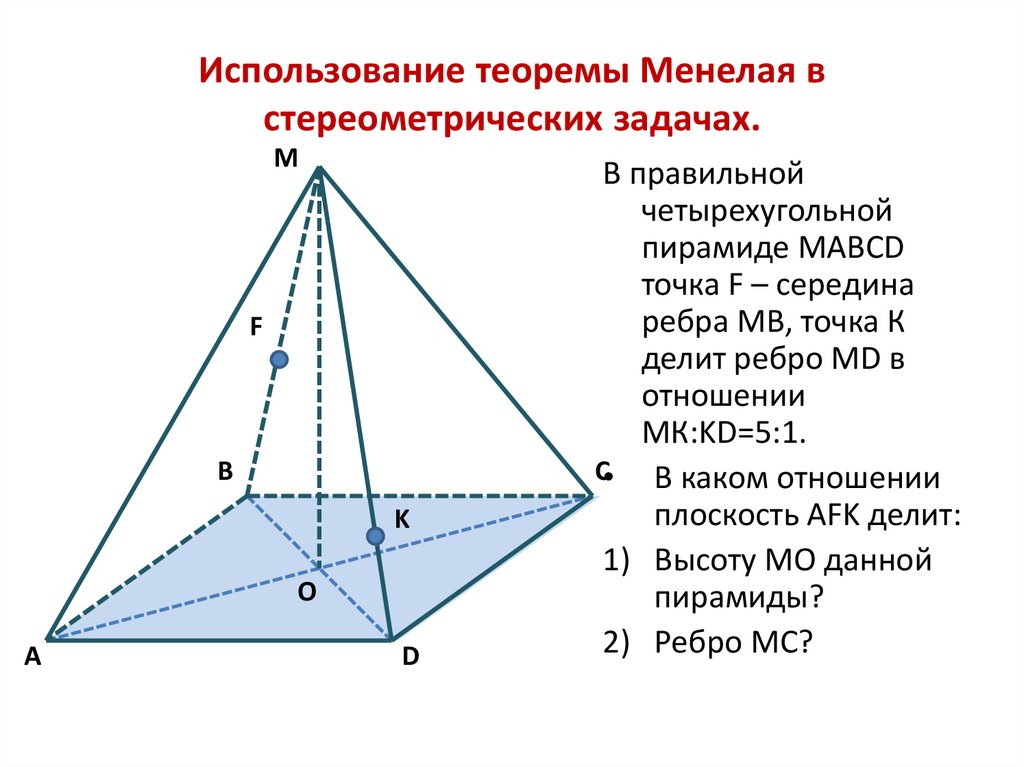
В правильной
четырехугольной
пирамиде MABCD
точка F – середина
ребра МВ, точка К
делит ребро МD в
отношении
МК:KD=5:1.
C• В каком отношении
плоскость АFK делит:
1) Высоту МО данной
пирамиды?
2) Ребро МС?
9.
Использование теоремы Менелая встереометрических задачах.
M
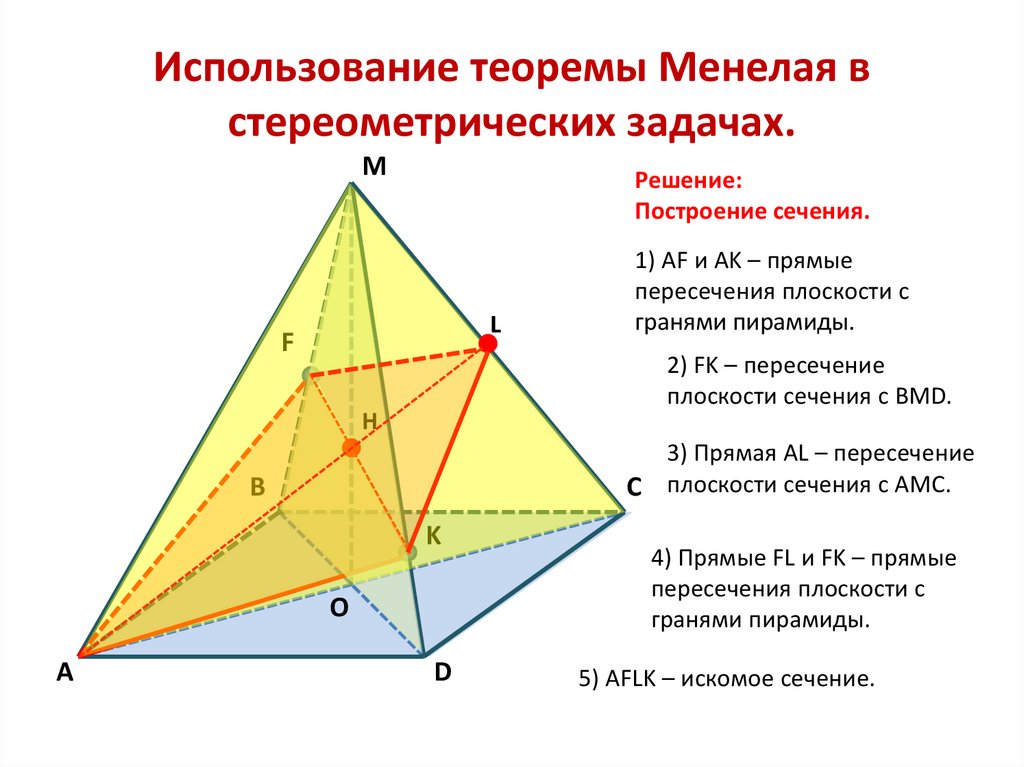
Решение:
Построение сечения.
L
F
2) FK – пересечение
плоскости сечения с BMD.
Н
3) Прямая AL – пересечение
C плоскости сечения с АМС.
B
K
O
A
1) AF и AK – прямые
пересечения плоскости с
гранями пирамиды.
D
4) Прямые FL и FK – прямые
пересечения плоскости с
гранями пирамиды.
5) AFLK – искомое сечение.
10.
Использование теоремы Менелая встереометрических задачах.
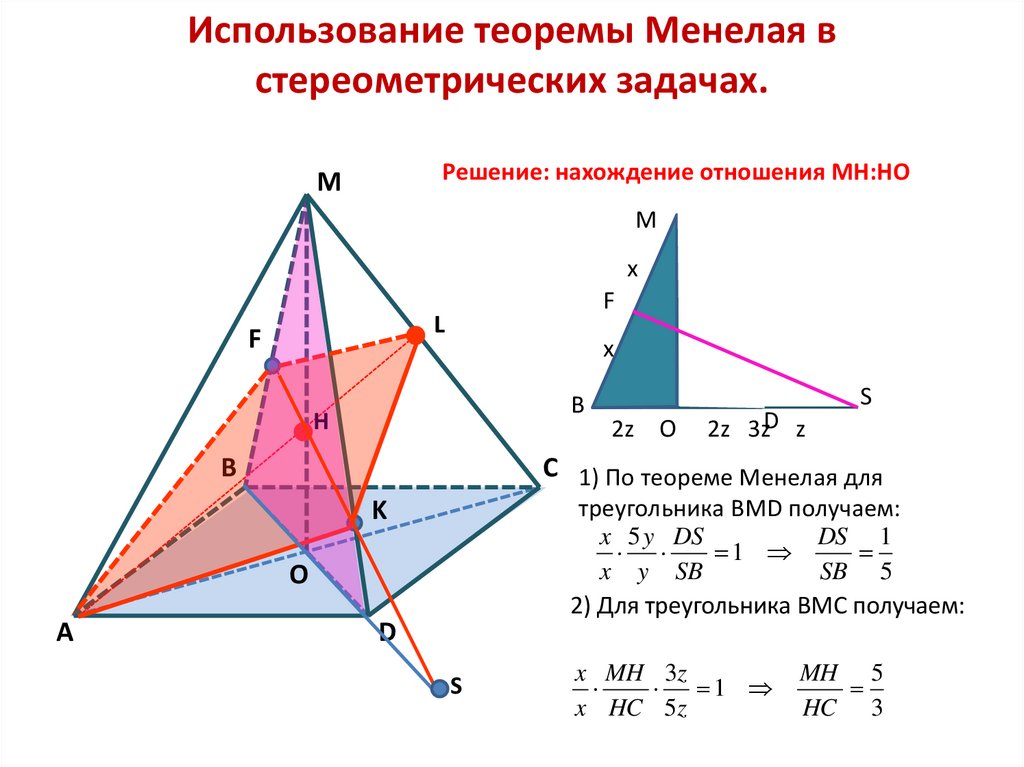
Решение: нахождение отношения МН:НО
M
M
x
F
L
F
x
B
Н
B
Н
K
y
2z О
2z 3zD z
S
C 1) По теореме Менелая для
треугольника ВMD получаем:
x 5 y DS
DS 1
1
x y SB
SB 5
2) Для треугольника ВМС получаем:
K
O
A
5y
D
S
x MH 3z
1
x HC 5z
MH 5
HC 3
11.
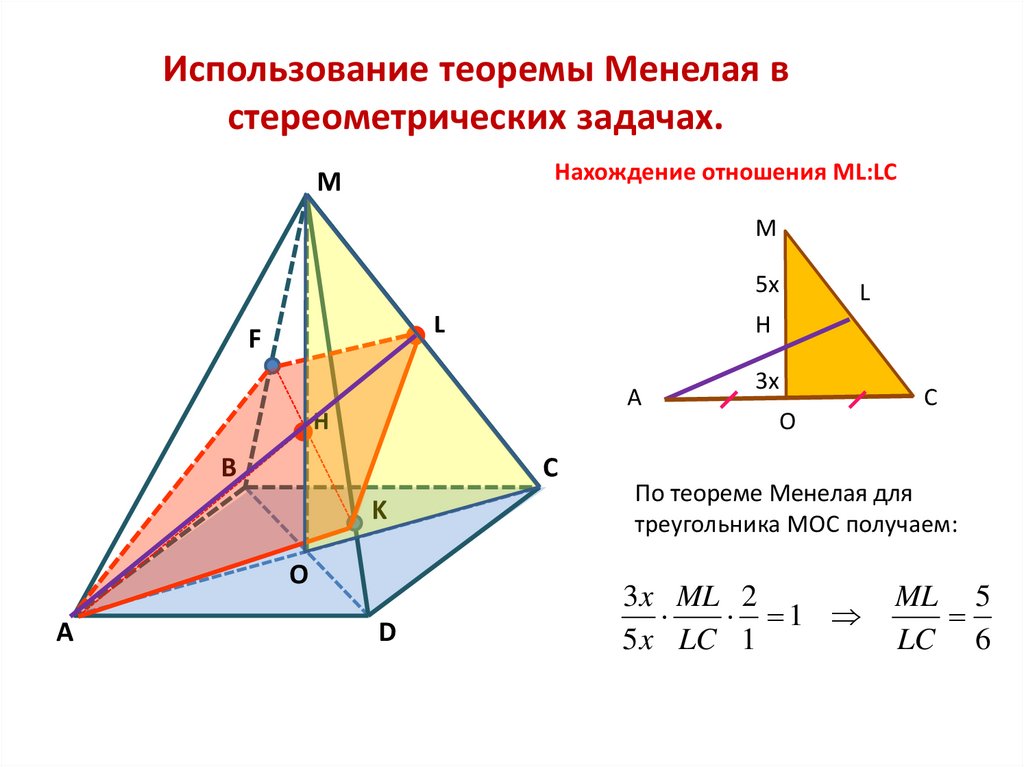
Использование теоремы Менелая встереометрических задачах.
Нахождение отношения ML:LC
M
М
5x
L
F
Н
А
Н
B
C
3x
О
C
K
По теореме Менелая для
треугольника МОС получаем:
D
3x ML 2
1
5 x LC 1
O
A
L
ML 5
LC 6


 Математика
Математика








