Похожие презентации:
Взаимное расположение прямых, метод прямоугольного треугольника, точка и прямая (лекция 2)
1.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХМЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ТОЧКА И ПРЯМАЯ.
ПЛОСКОСТЬ. СПОСОБЫ ЗАДАНИЯ
Лекция 2
2.
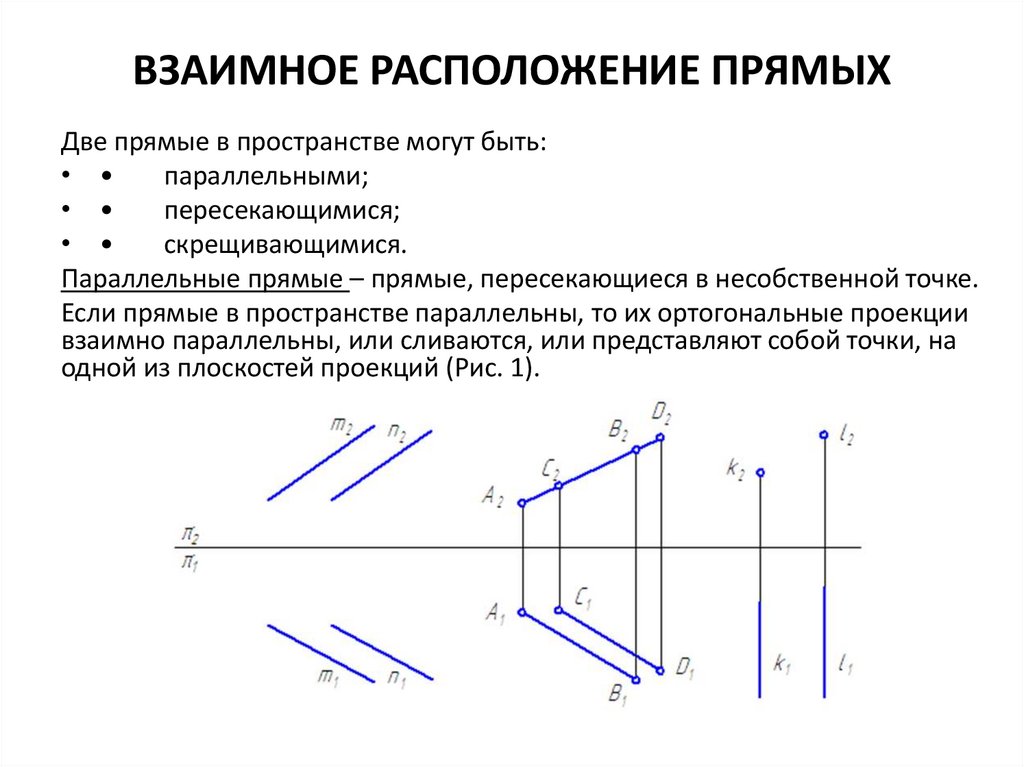
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХДве прямые в пространстве могут быть:
•
параллельными;
•
пересекающимися;
•
скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
Если прямые в пространстве параллельны, то их ортогональные проекции
взаимно параллельны, или сливаются, или представляют собой точки, на
одной из плоскостей проекций (Рис. 1).
3.
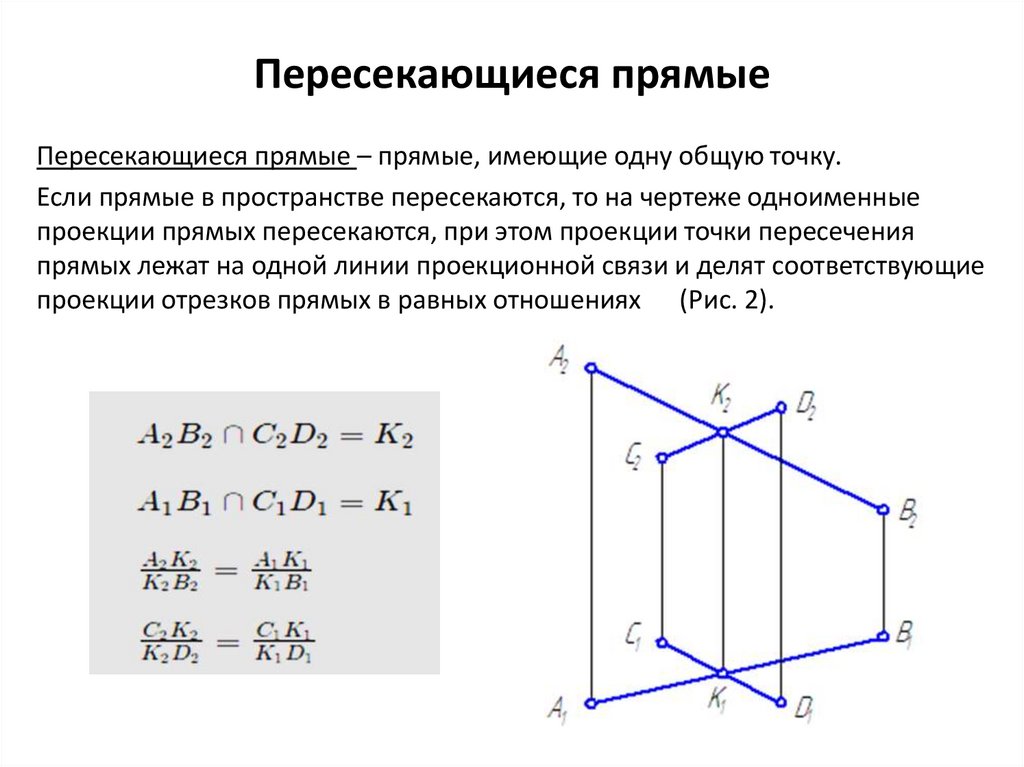
Пересекающиеся прямыеПересекающиеся прямые – прямые, имеющие одну общую точку.
Если прямые в пространстве пересекаются, то на чертеже одноименные
проекции прямых пересекаются, при этом проекции точки пересечения
прямых лежат на одной линии проекционной связи и делят соответствующие
проекции отрезков прямых в равных отношениях (Рис. 2).
4.
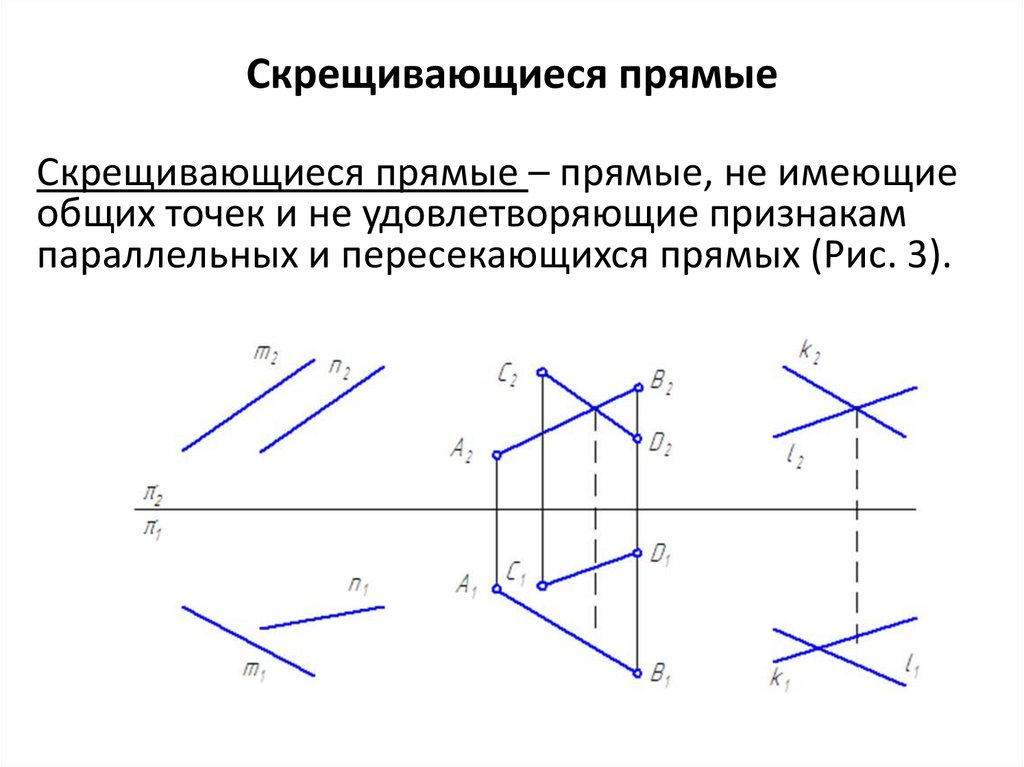
Скрещивающиеся прямыеСкрещивающиеся прямые – прямые, не имеющие
общих точек и не удовлетворяющие признакам
параллельных и пересекающихся прямых (Рис. 3).
5.
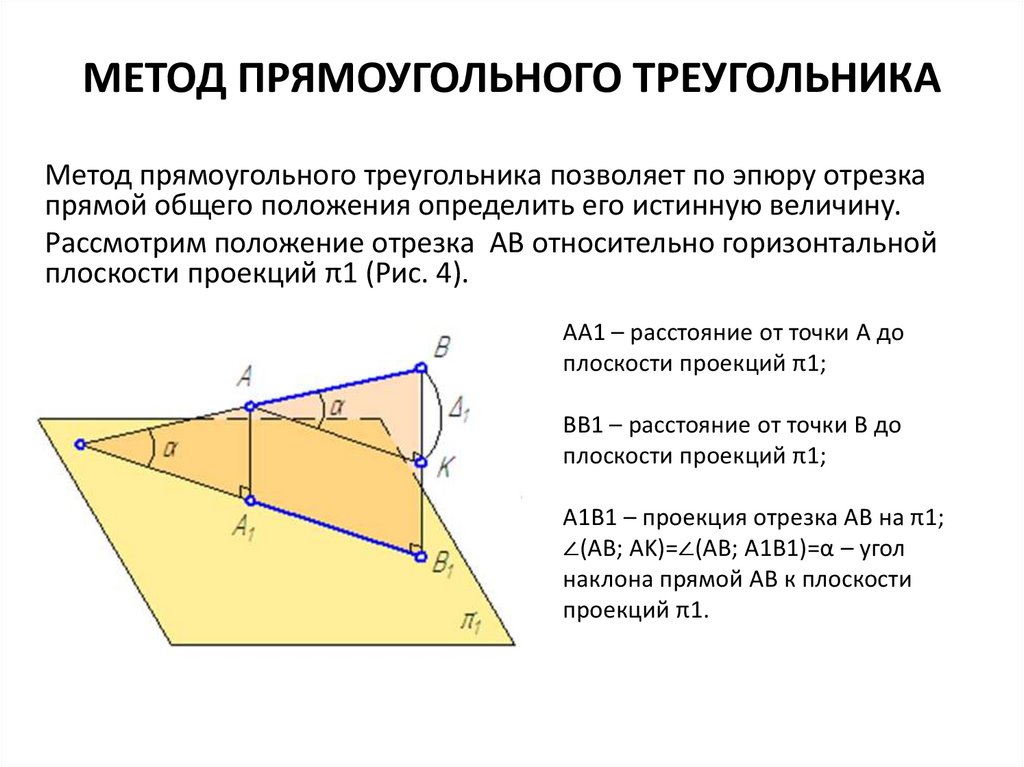
МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАМетод прямоугольного треугольника позволяет по эпюру отрезка
прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной
плоскости проекций π1 (Рис. 4).
АА1 – расстояние от точки А до
плоскости проекций π1;
ВВ1 – расстояние от точки В до
плоскости проекций π1;
А1В1 – проекция отрезка АВ на π1;
∠(AB; AK)=∠(AB; A1B1)=α – угол
наклона прямой АВ к плоскости
проекций π1.
6.
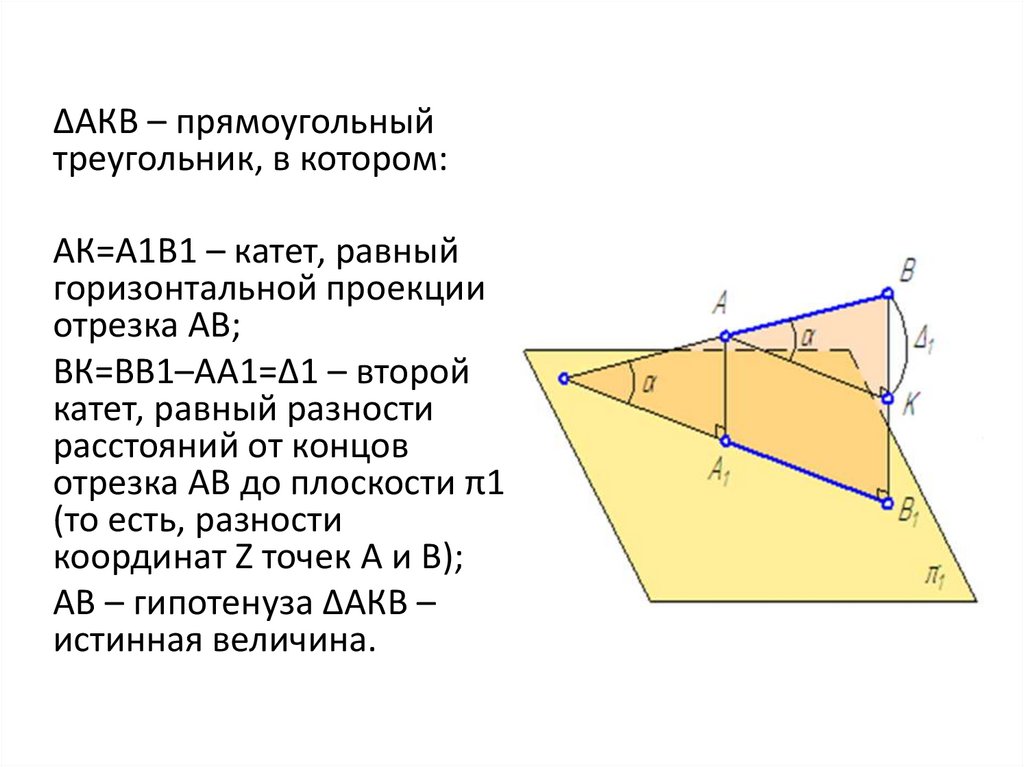
ΔАКВ – прямоугольныйтреугольник, в котором:
АК=А1В1 – катет, равный
горизонтальной проекции
отрезка АВ;
ВК=ВВ1–АА1=Δ1 – второй
катет, равный разности
расстояний от концов
отрезка АВ до плоскости π1
(то есть, разности
координат Z точек А и В);
АВ – гипотенуза ΔАКВ –
истинная величина.
7.
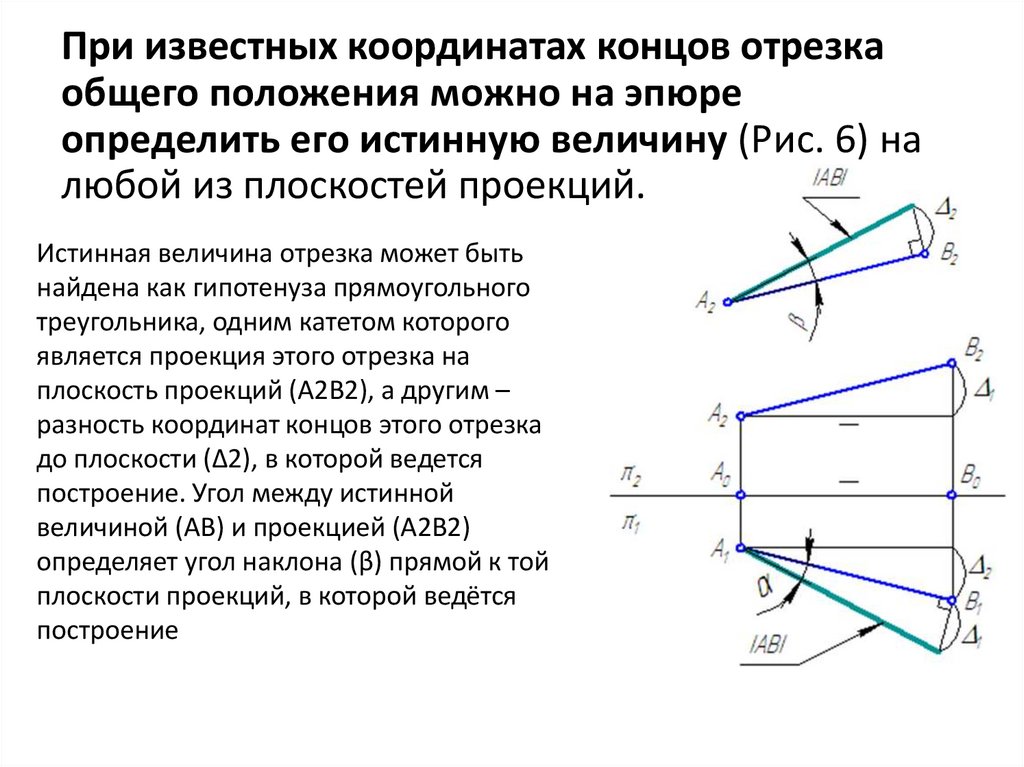
При известных координатах концов отрезкаобщего положения можно на эпюре
определить его истинную величину (Рис. 6) на
любой из плоскостей проекций.
Истинная величина отрезка может быть
найдена как гипотенуза прямоугольного
треугольника, одним катетом которого
является проекция этого отрезка на
плоскость проекций (А2В2), а другим –
разность координат концов этого отрезка
до плоскости (Δ2), в которой ведется
построение. Угол между истинной
величиной (АВ) и проекцией (А2В2)
определяет угол наклона (β) прямой к той
плоскости проекций, в которой ведётся
построение
8.
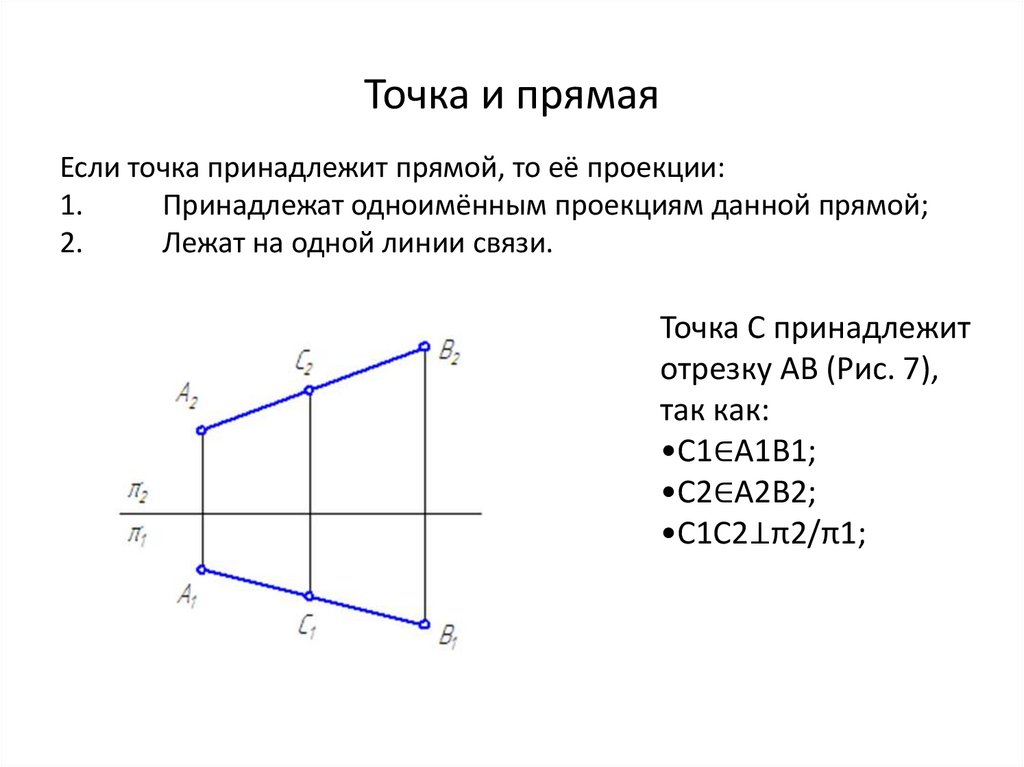
Точка и прямаяЕсли точка принадлежит прямой, то её проекции:
1.
Принадлежат одноимённым проекциям данной прямой;
2.
Лежат на одной линии связи.
Точка С принадлежит
отрезку АВ (Рис. 7),
так как:
•С1∈А1В1;
•С2∈А2В2;
•С1С2⊥π2/π1;
9.
Если точка делит отрезок в каком-либоотношении, то проекции этой точки делят
одноименные проекции данного отрезка в
том же отношении:
• C2B2A2C2=C1B1A1C1
Справедливо и обратное утверждение.
10.
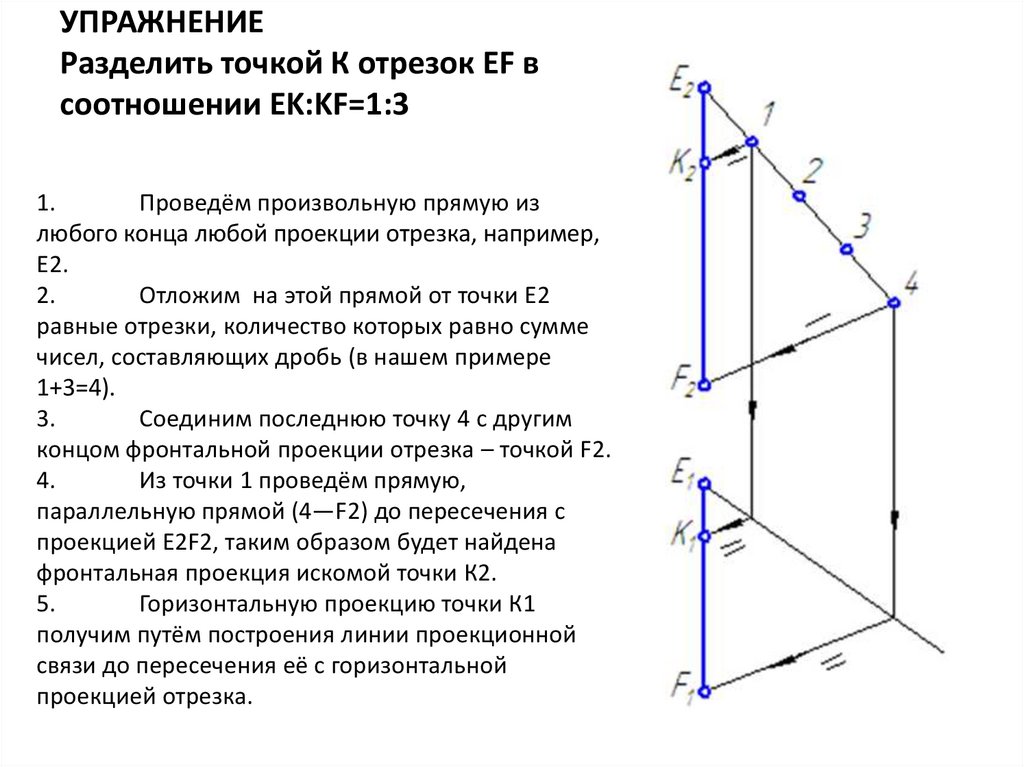
УПРАЖНЕНИЕРазделить точкой К отрезок EF в
соотношении EK:KF=1:3
1.
Проведём произвольную прямую из
любого конца любой проекции отрезка, например,
Е2.
2.
Отложим на этой прямой от точки Е2
равные отрезки, количество которых равно сумме
чисел, составляющих дробь (в нашем примере
1+3=4).
3.
Соединим последнюю точку 4 с другим
концом фронтальной проекции отрезка – точкой F2.
4.
Из точки 1 проведём прямую,
параллельную прямой (4—F2) до пересечения с
проекцией E2F2, таким образом будет найдена
фронтальная проекция искомой точки К2.
5.
Горизонтальную проекцию точки К1
получим путём построения линии проекционной
связи до пересечения её с горизонтальной
проекцией отрезка.
11.
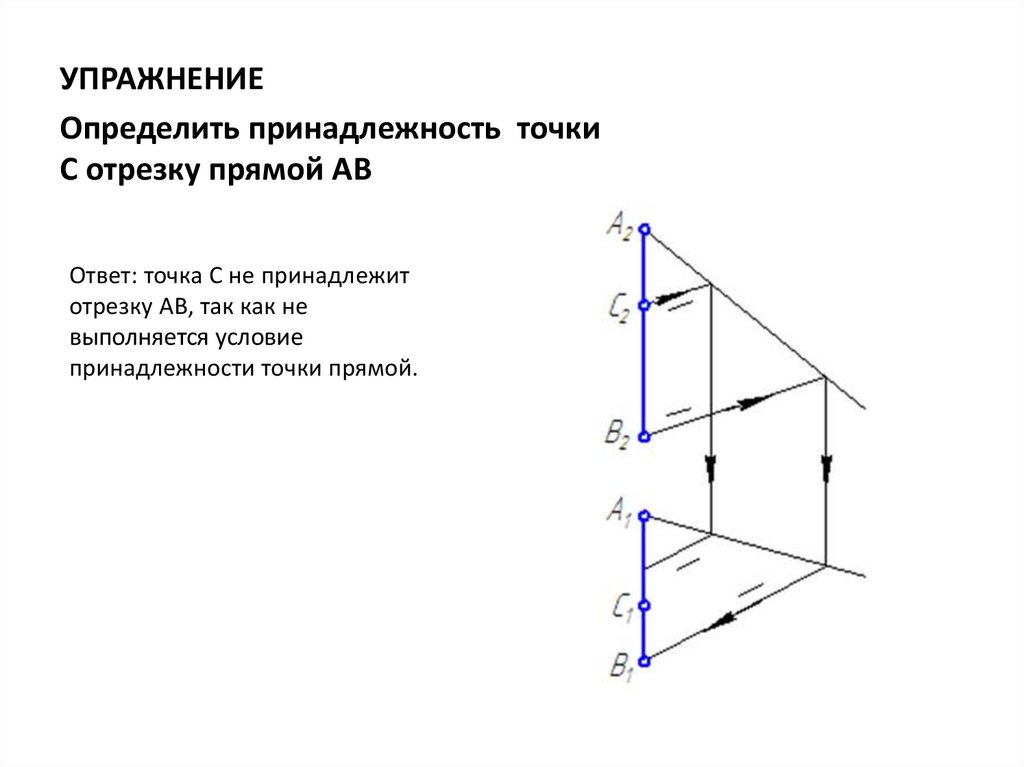
УПРАЖНЕНИЕОпределить принадлежность точки
С отрезку прямой АВ
Ответ: точка С не принадлежит
отрезку АВ, так как не
выполняется условие
принадлежности точки прямой.
12.
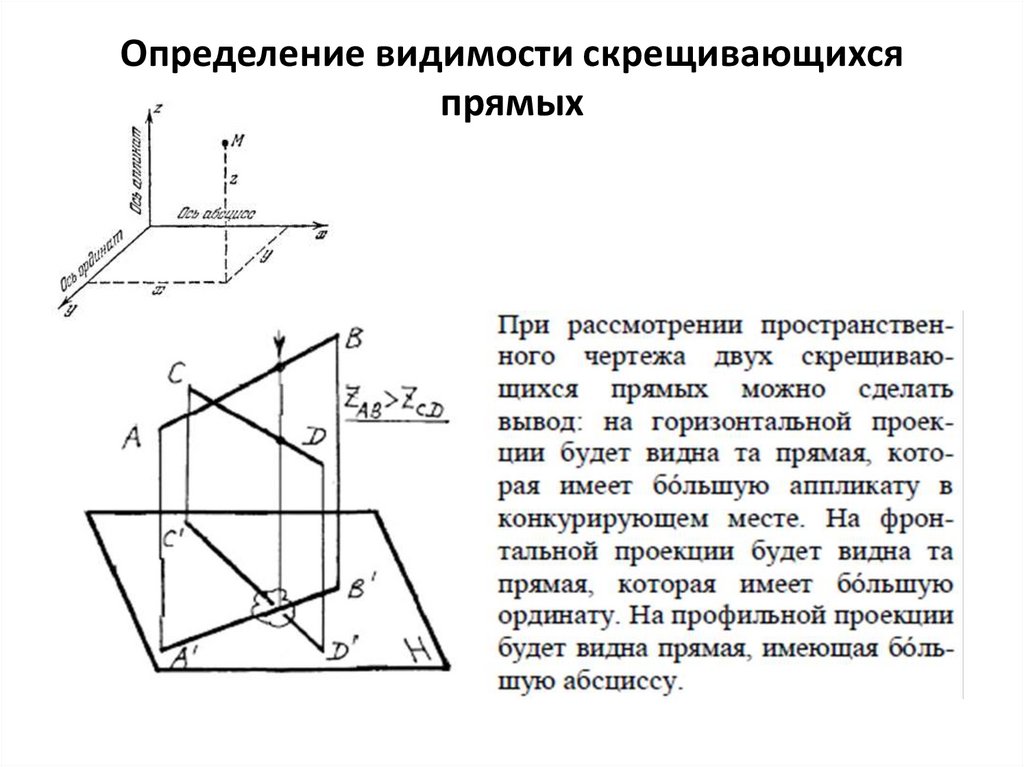
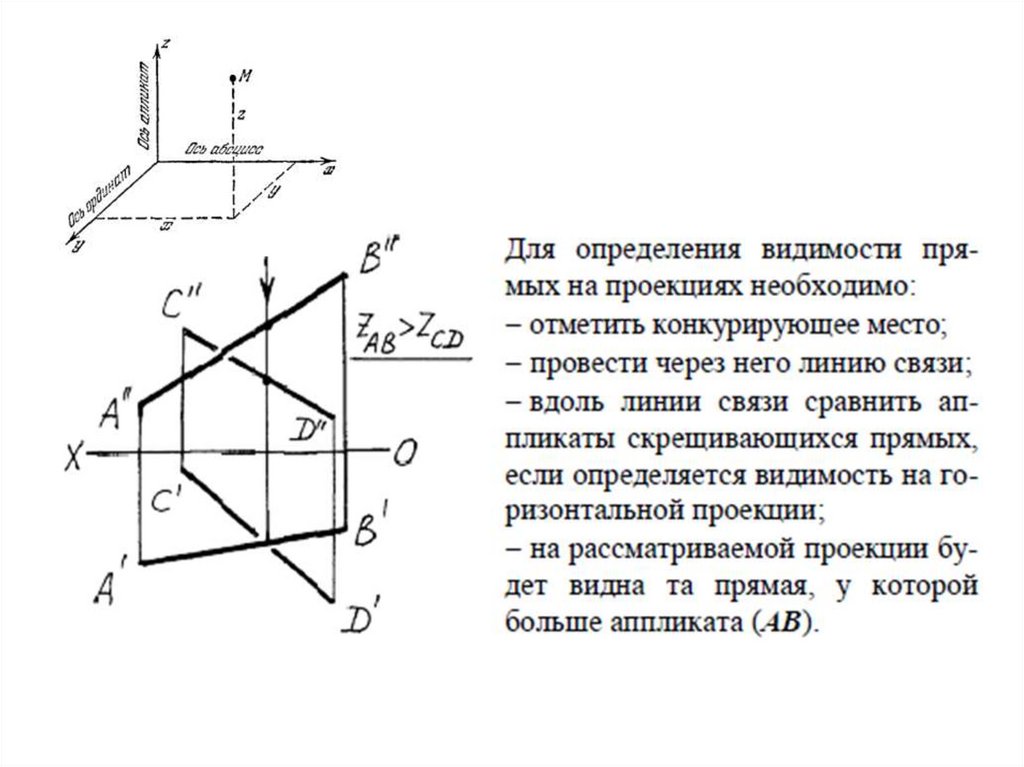
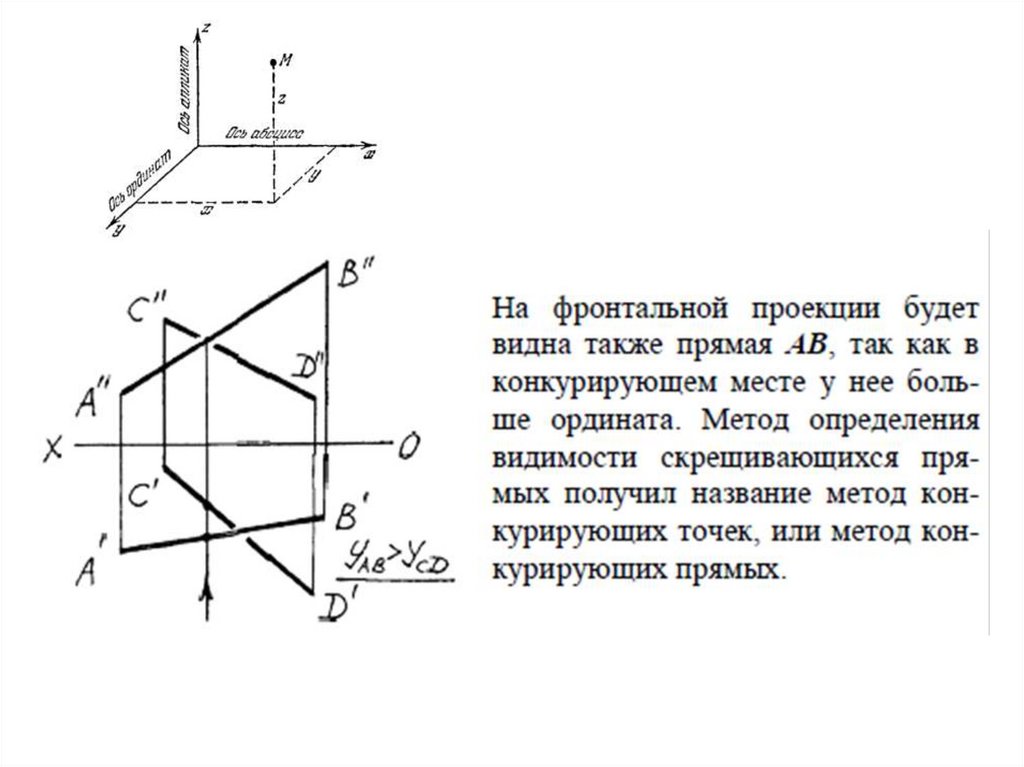
Определение видимости скрещивающихсяпрямых
13.
14.
15.
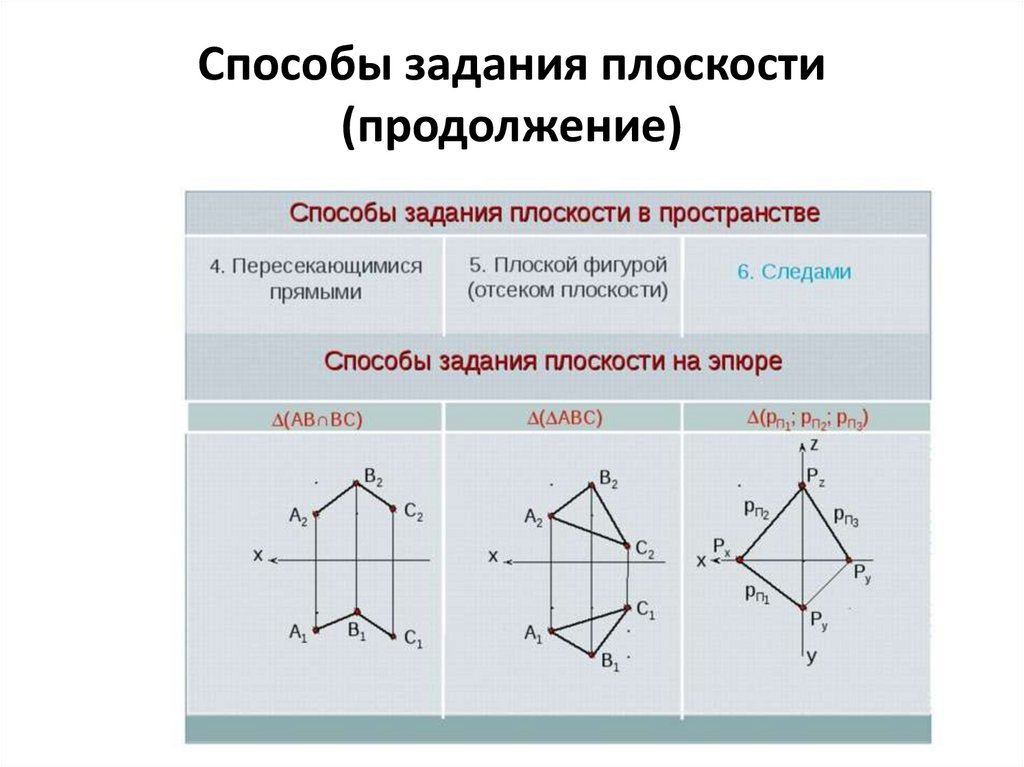
Способы задания плоскости16.
Способы задания плоскости(продолжение)
17.
Плоскости общего и частного положенияПлоскость общего положения
• Плоскостью общего положения называется
плоскость, не перпендикулярная и не
параллельная ни одной из плоскостей проекций,
а значит, расположенная под произвольным
углом к каждой из них.
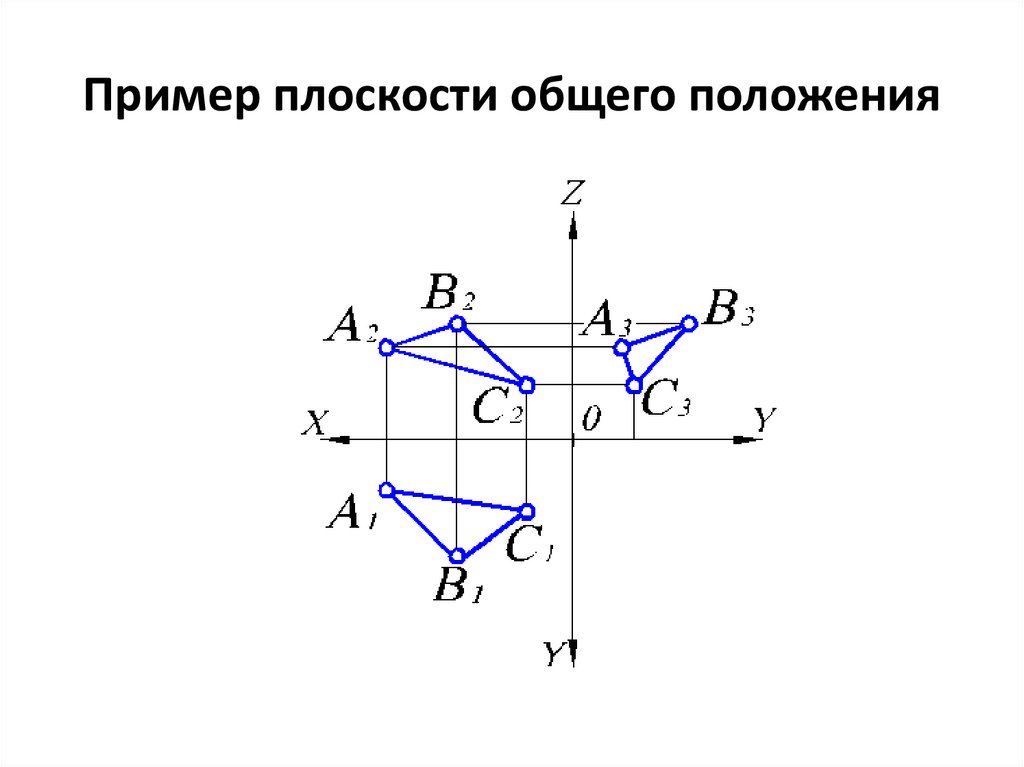
• У такой плоскости все проекции будут
невырожденные. Например, если плоскость
общего положения задана плоской фигурой
(треугольником), то все три проекции ее будут
треугольниками
18.
Пример плоскости общего положения19.
Плоскости частного положения плоскости уровня• Плоскостью частного положения называется плоскость,
занимающая частное положение в пространстве, т.е.
параллельная или перпендикулярная одной из плоскостей
проекций.
• Плоскостью уровня называется плоскость, параллельная
одной из плоскостей проекций, а следовательно,
перпендикулярная двум другим. Тогда проекциями
плоскости уровня будут прямые, параллельные
соответствующим осям, вне зависимости от того, чем
задана плоскость. От способа задания плоскости зависит
лишь ее проекция на ту плоскость проекций, которой
заданная плоскость параллельна.
20.
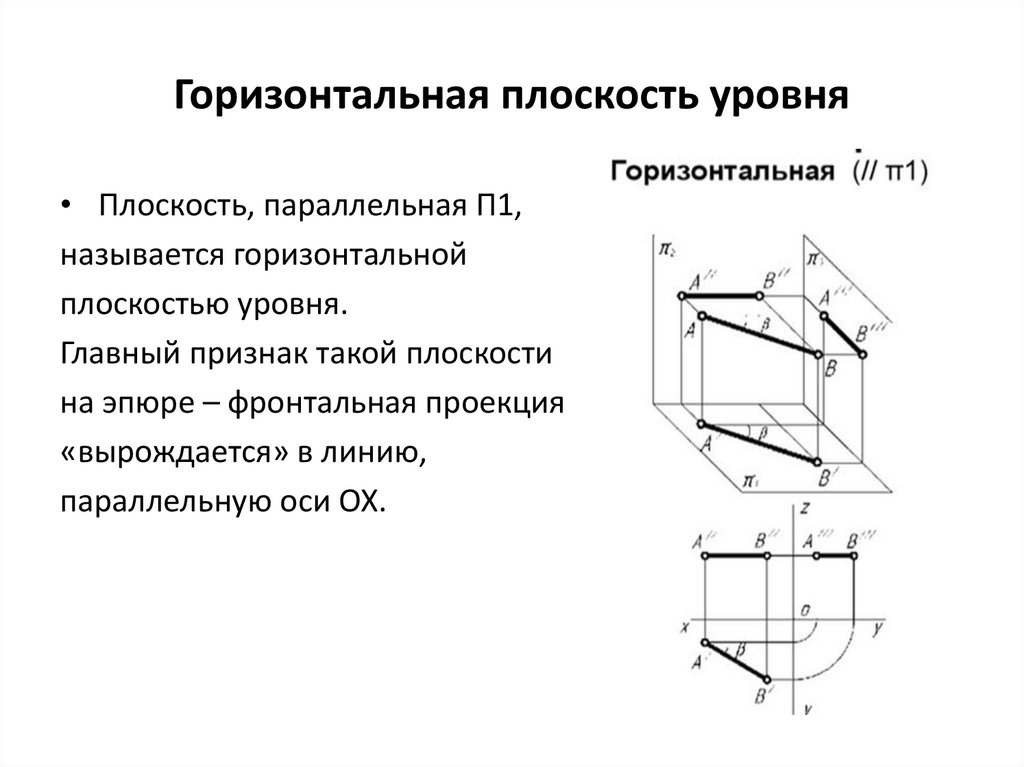
Горизонтальная плоскость уровня• Плоскость, параллельная П1,
называется горизонтальной
плоскостью уровня.
Главный признак такой плоскости
на эпюре – фронтальная проекция
«вырождается» в линию,
параллельную оси ОХ.
21.
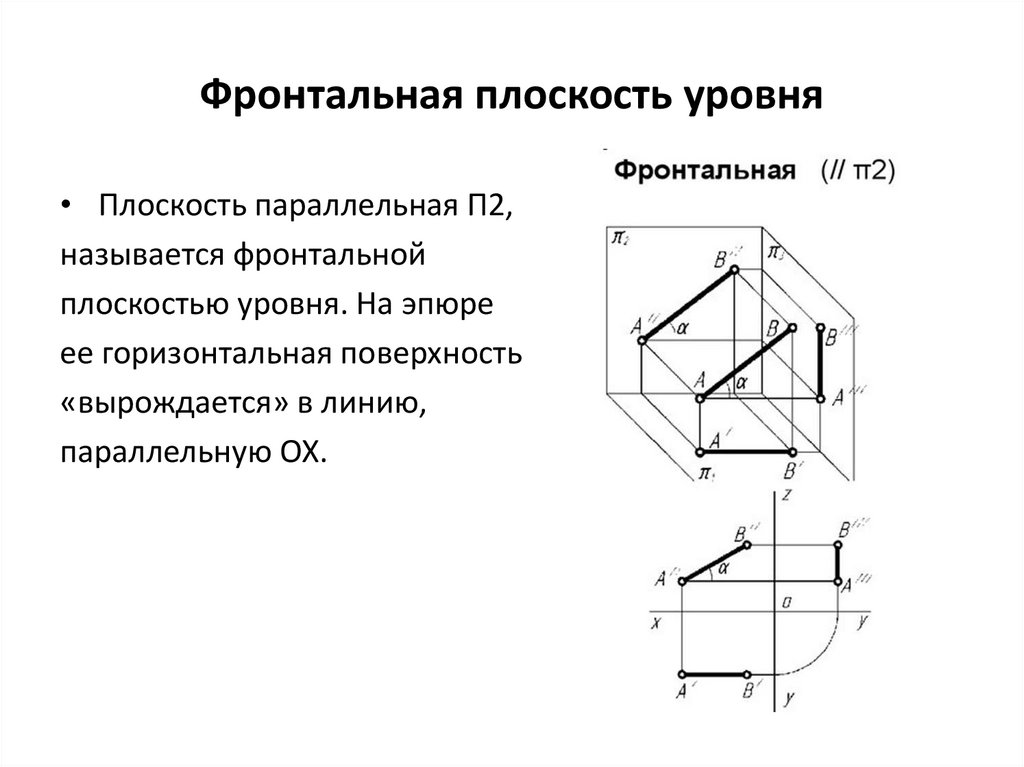
Фронтальная плоскость уровня• Плоскость параллельная П2,
называется фронтальной
плоскостью уровня. На эпюре
ее горизонтальная поверхность
«вырождается» в линию,
параллельную ОХ.
22.
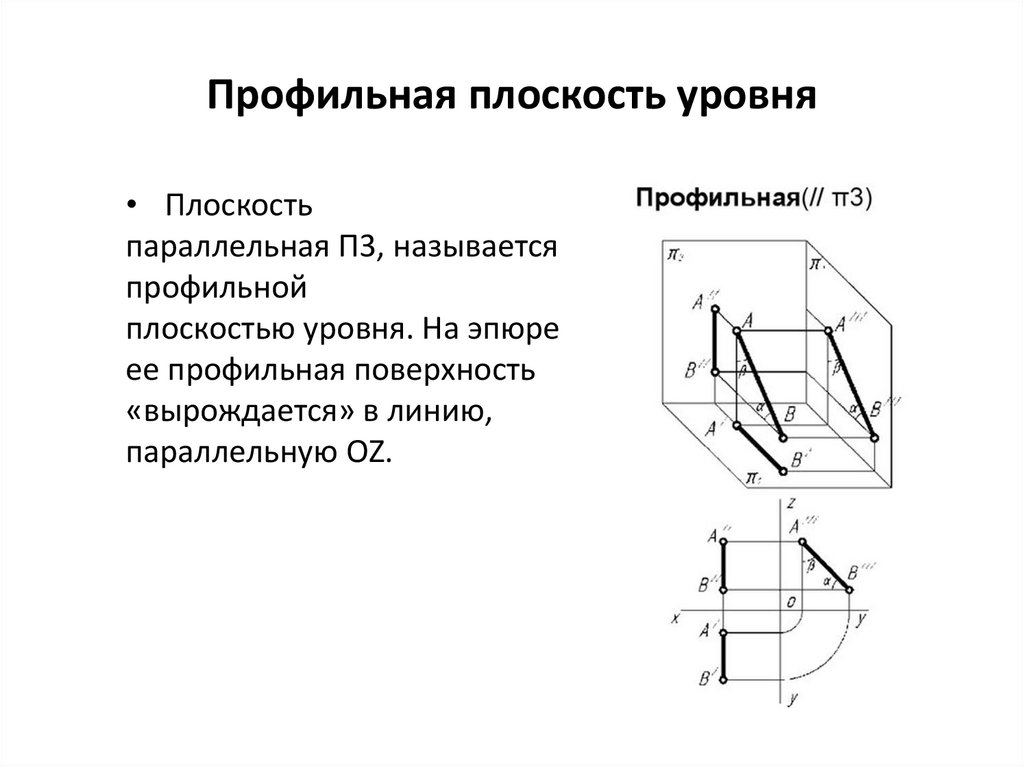
Профильная плоскость уровня• Плоскость
параллельная П3, называется
профильной
плоскостью уровня. На эпюре
ее профильная поверхность
«вырождается» в линию,
параллельную ОZ.
23.
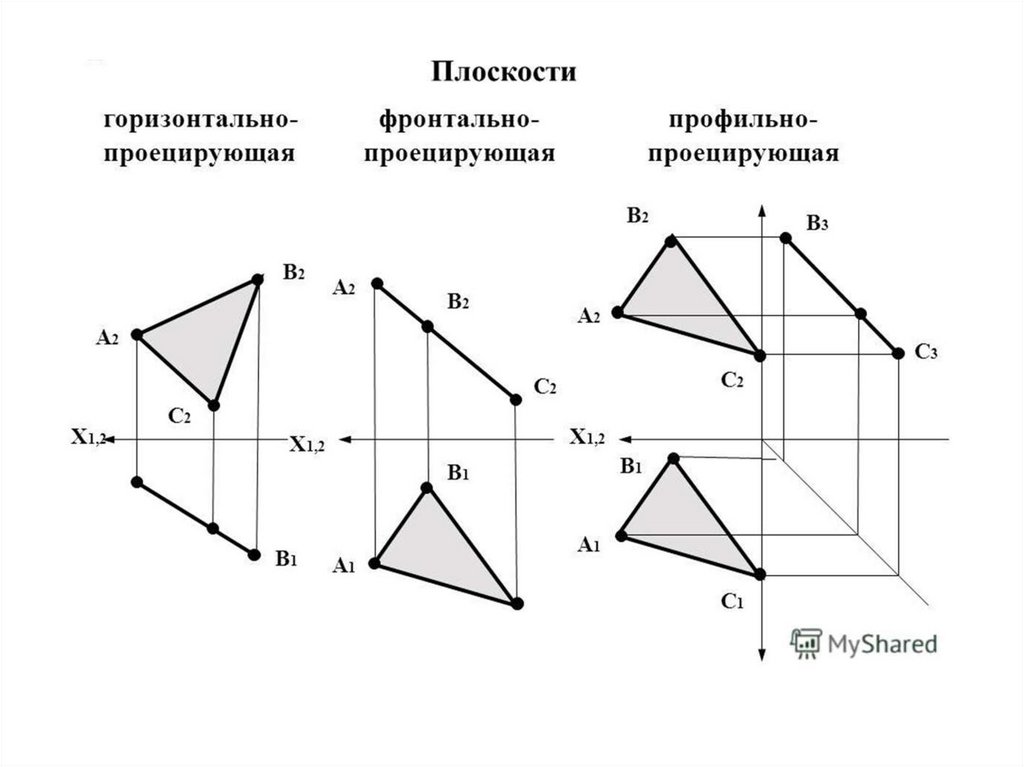
Проецирующие плоскости• Плоскости, перпендикулярные плоскостям
проекций, называются проецирующими. По
аналогии с прямой различают горизонтально-,
фронтально-, и профильно-проецирующие
плоскости. Главный признак проецирующих
плоскостей на эпюре – на одной из проекций
плоскость «вырождается» в линию.
Проецирующие следы перпендикулярны
соответствующим осям.
24.
25.
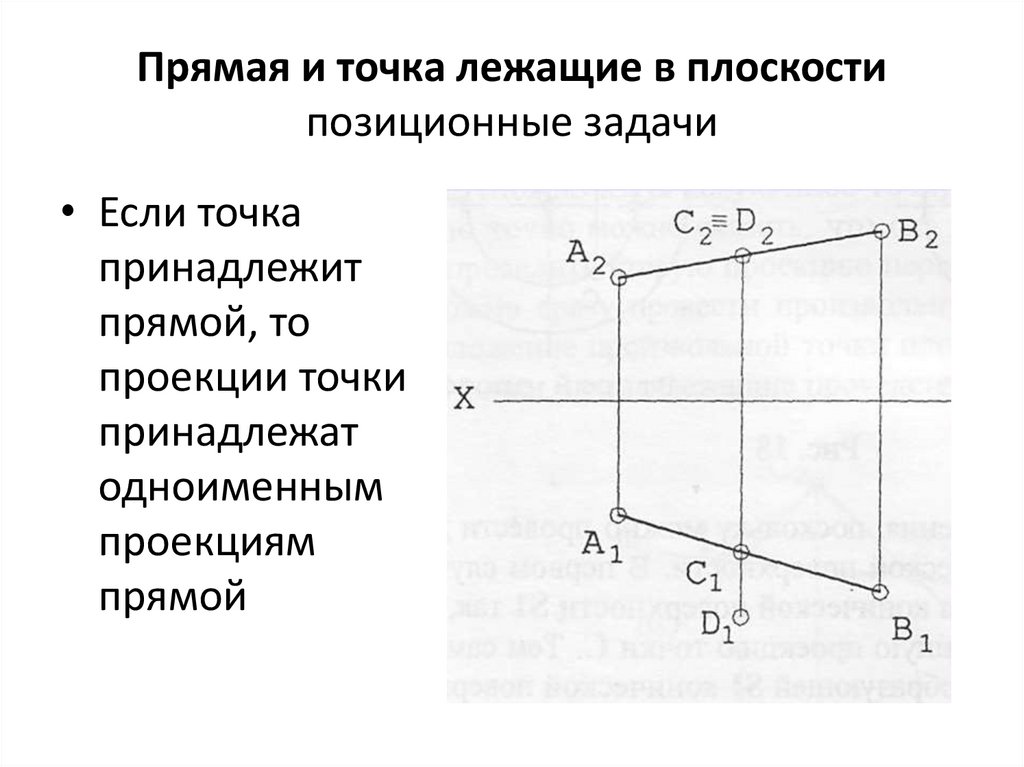
Прямая и точка лежащие в плоскостипозиционные задачи
• Если точка
принадлежит
прямой, то
проекции точки
принадлежат
одноименным
проекциям
прямой
26.
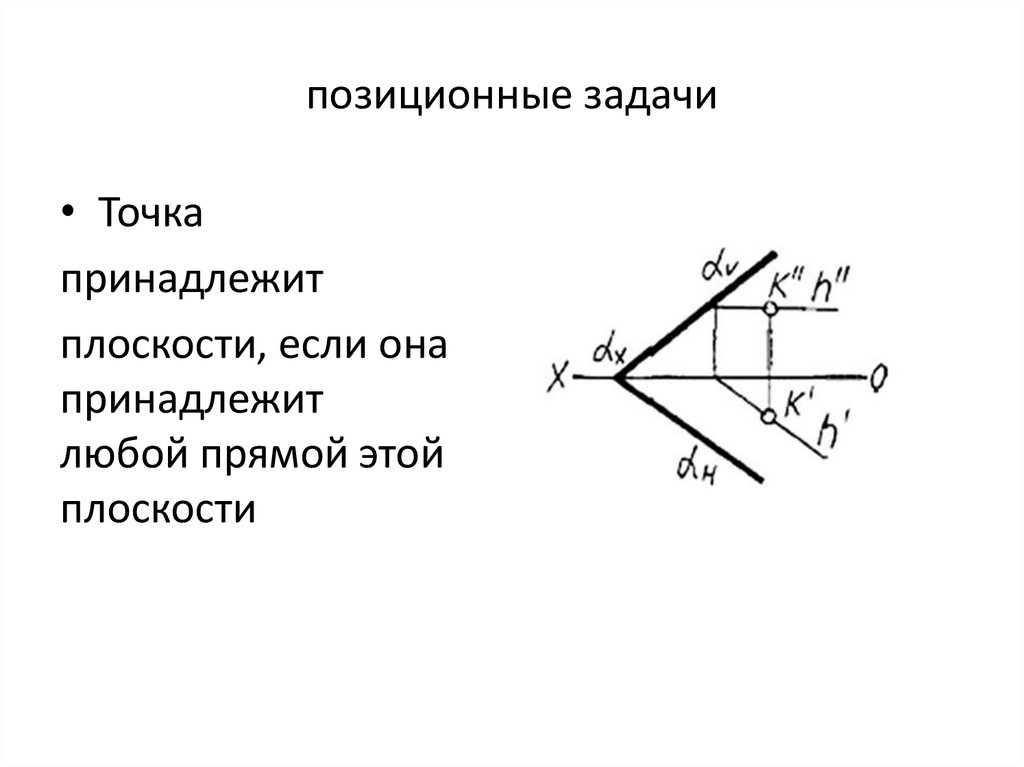
позиционные задачи• Точка
принадлежит
плоскости, если она
принадлежит
любой прямой этой
плоскости
27.
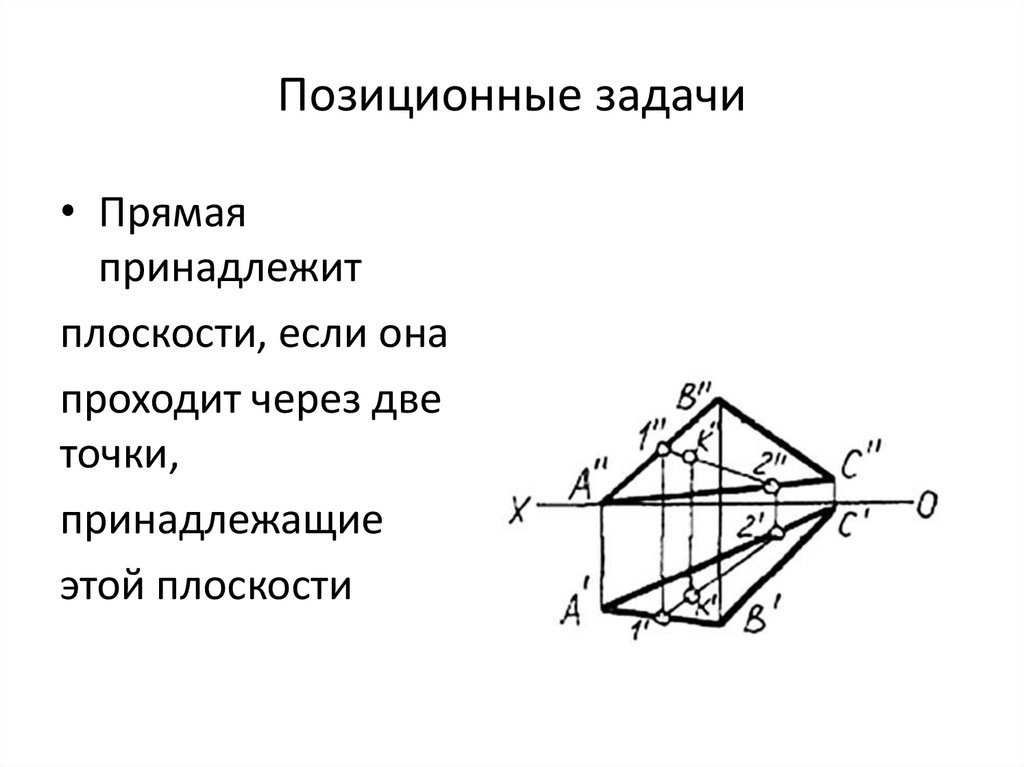
Позиционные задачи• Прямая
принадлежит
плоскости, если она
проходит через две
точки,
принадлежащие
этой плоскости
28.
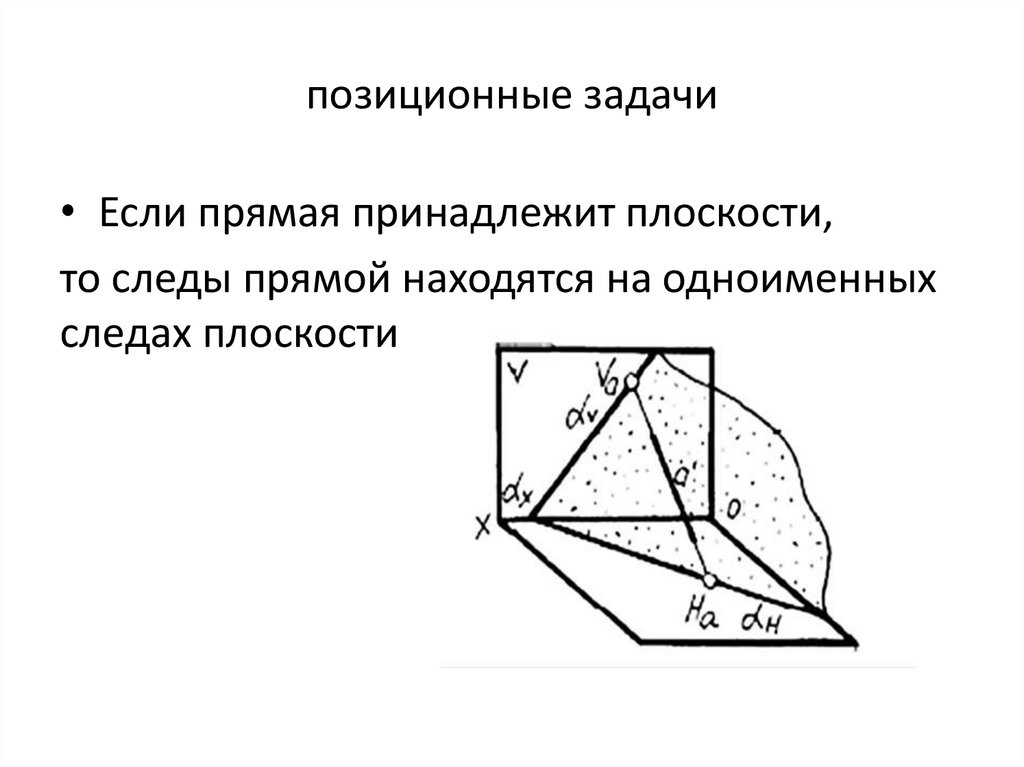
позиционные задачи• Если прямая принадлежит плоскости,
то следы прямой находятся на одноименных
следах плоскости
29.
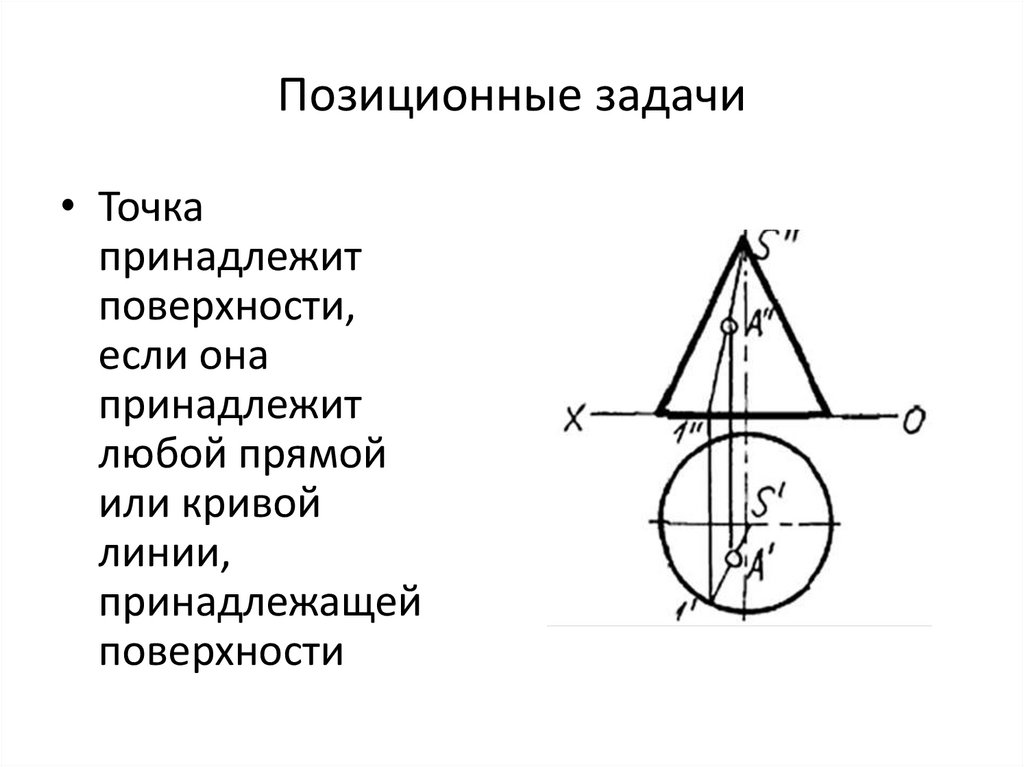
Позиционные задачи• Точка
принадлежит
поверхности,
если она
принадлежит
любой прямой
или кривой
линии,
принадлежащей
поверхности
30.
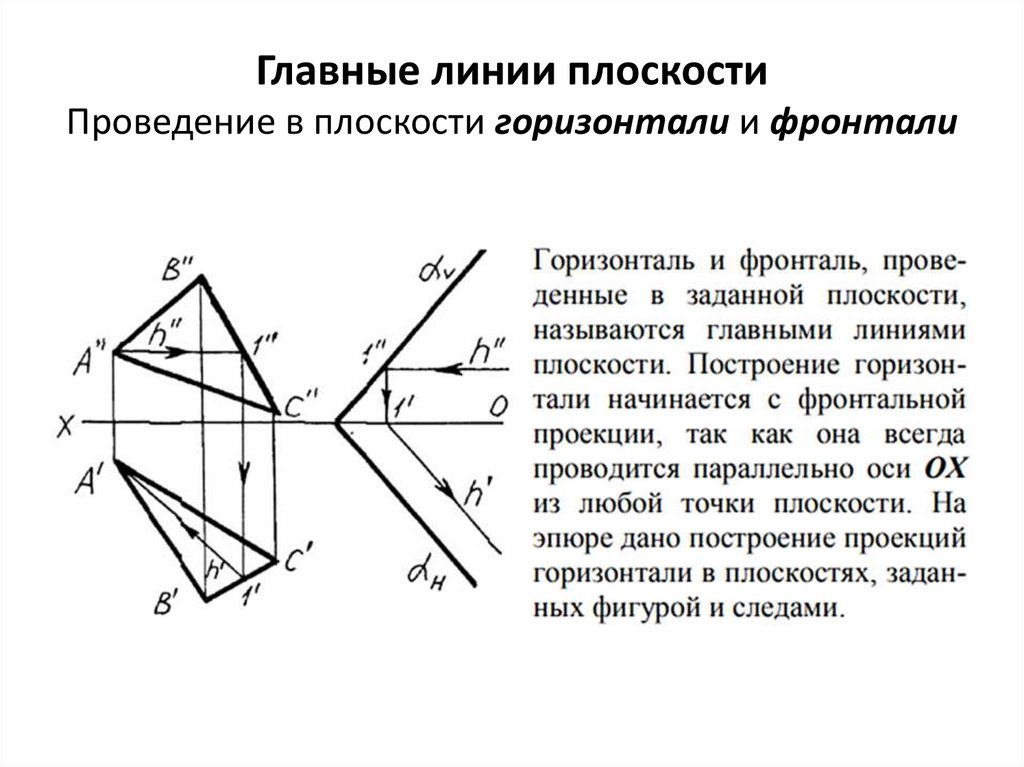
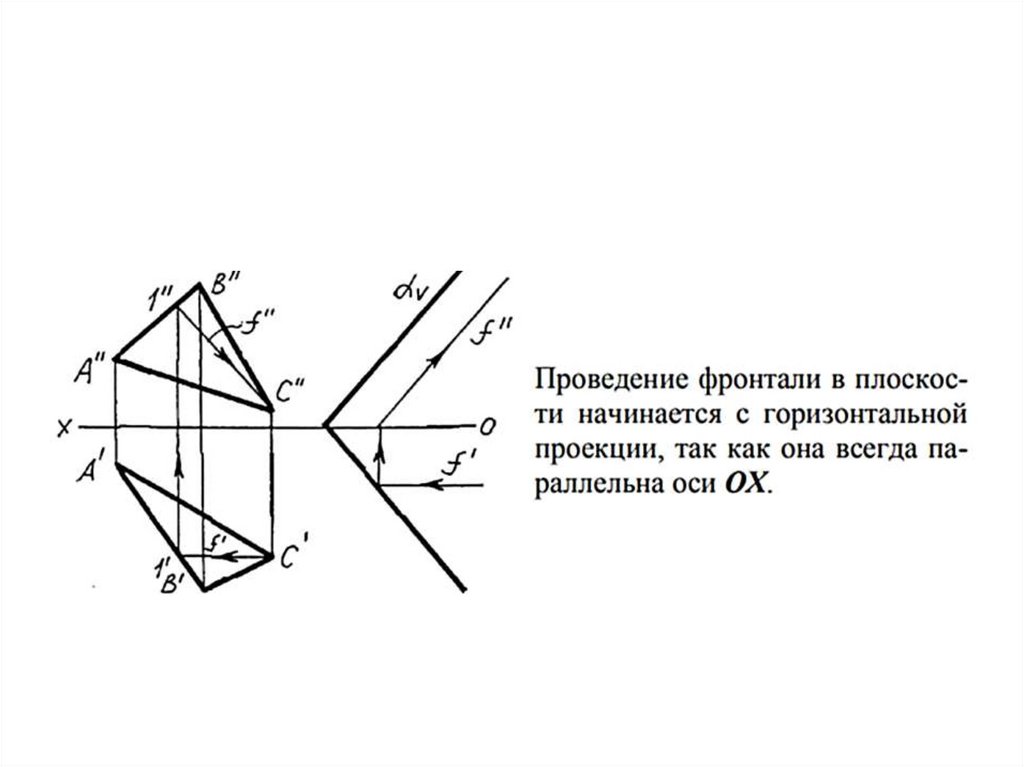
Главные линии плоскостиПроведение в плоскости горизонтали и фронтали
31.
32.
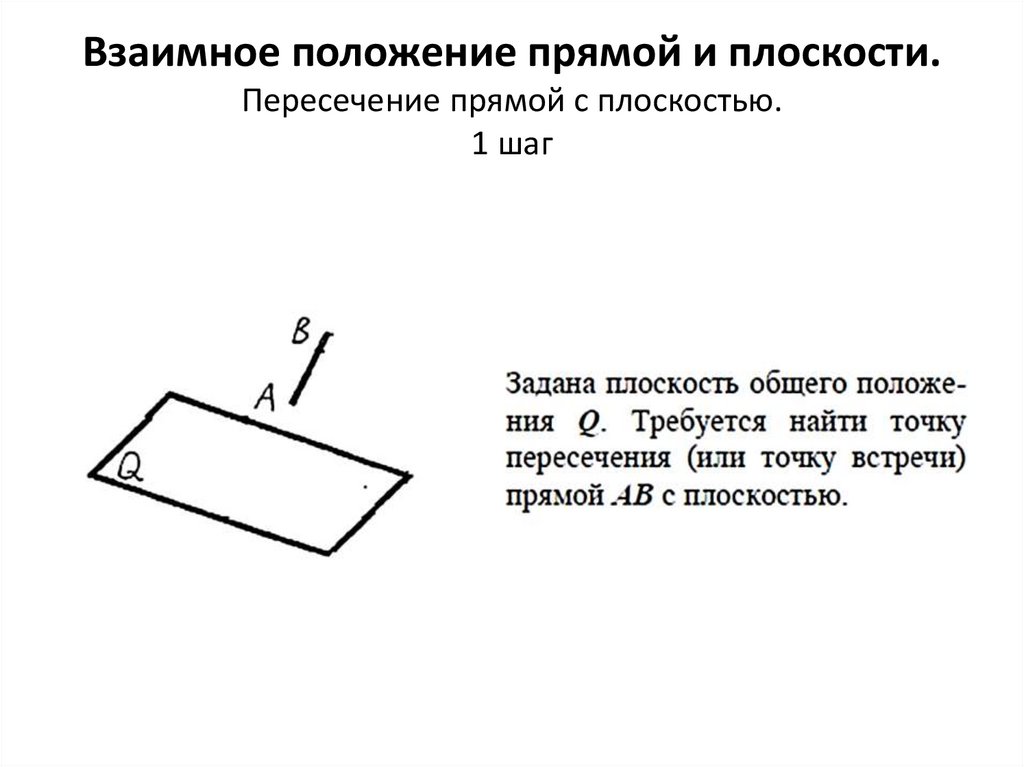
Взаимное положение прямой и плоскости.Пересечение прямой с плоскостью.
1 шаг
33.
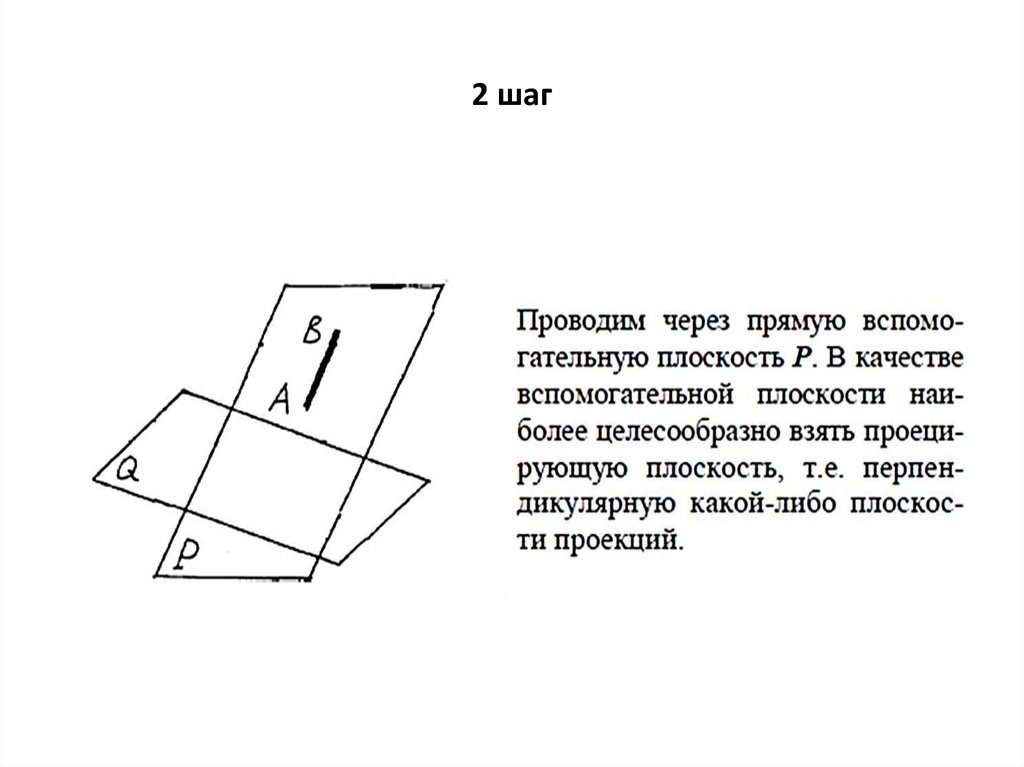
2 шаг34.
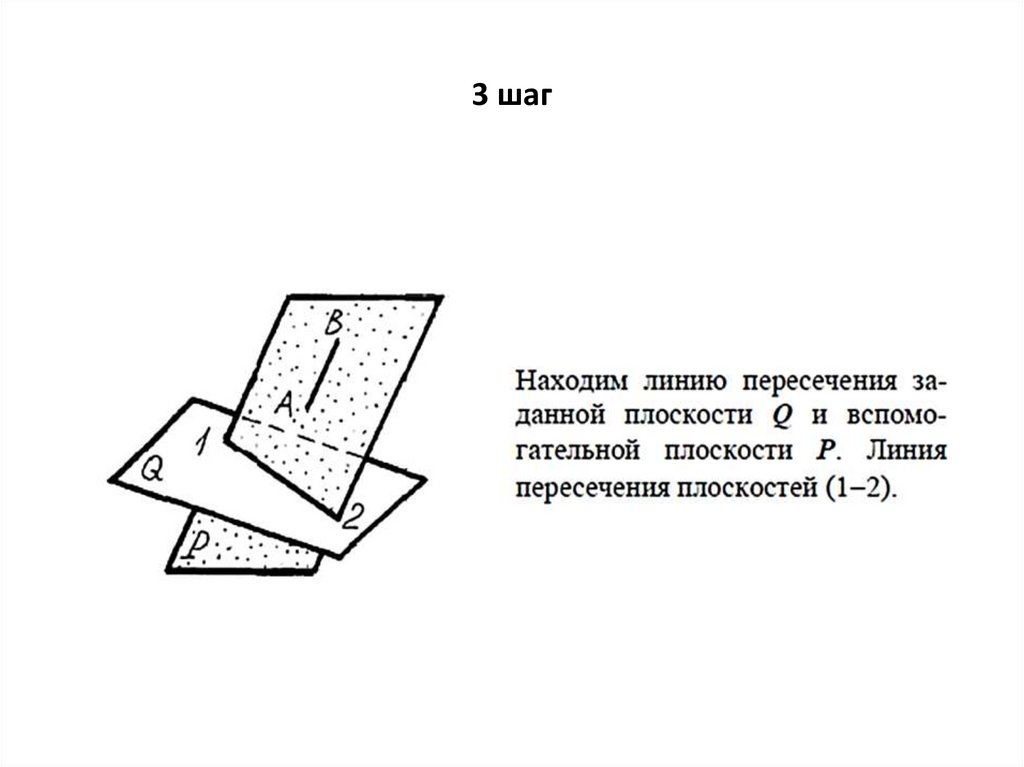
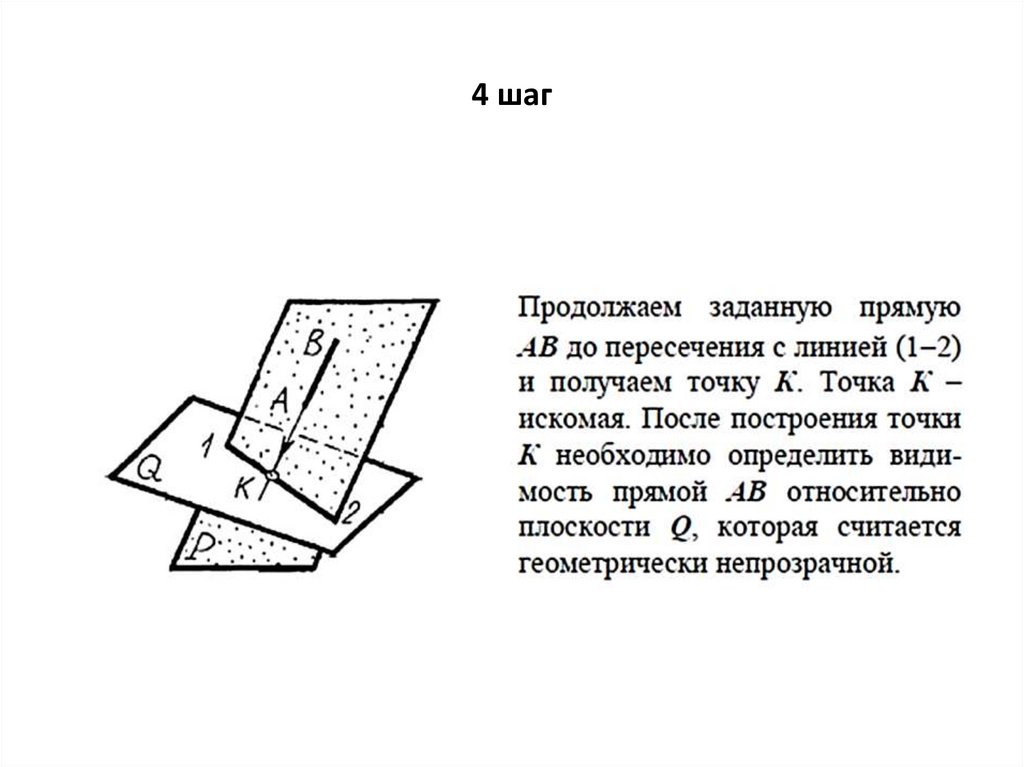
3 шаг35.
4 шаг36.
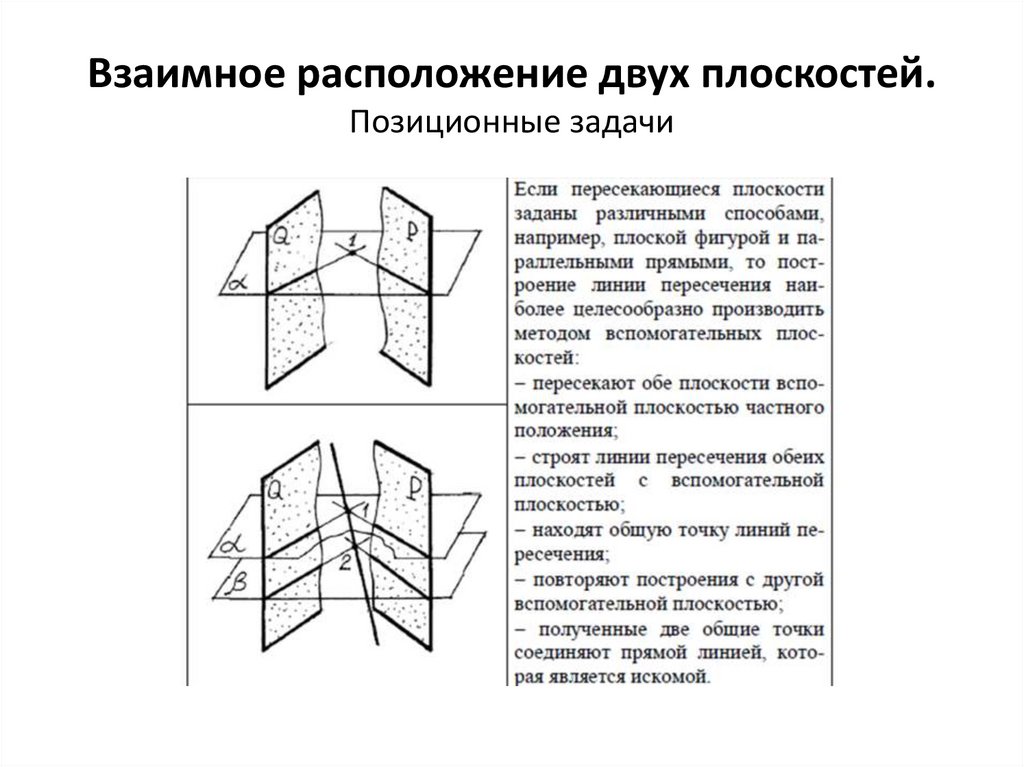
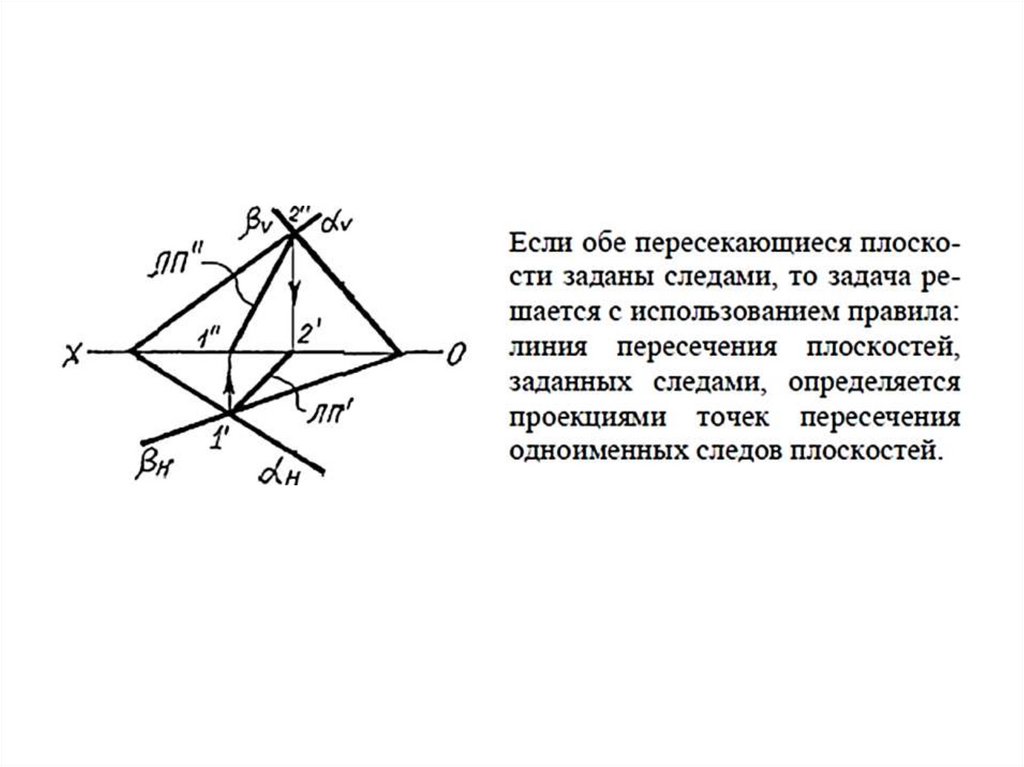
Взаимное расположение двух плоскостей.Позиционные задачи
37.
38.
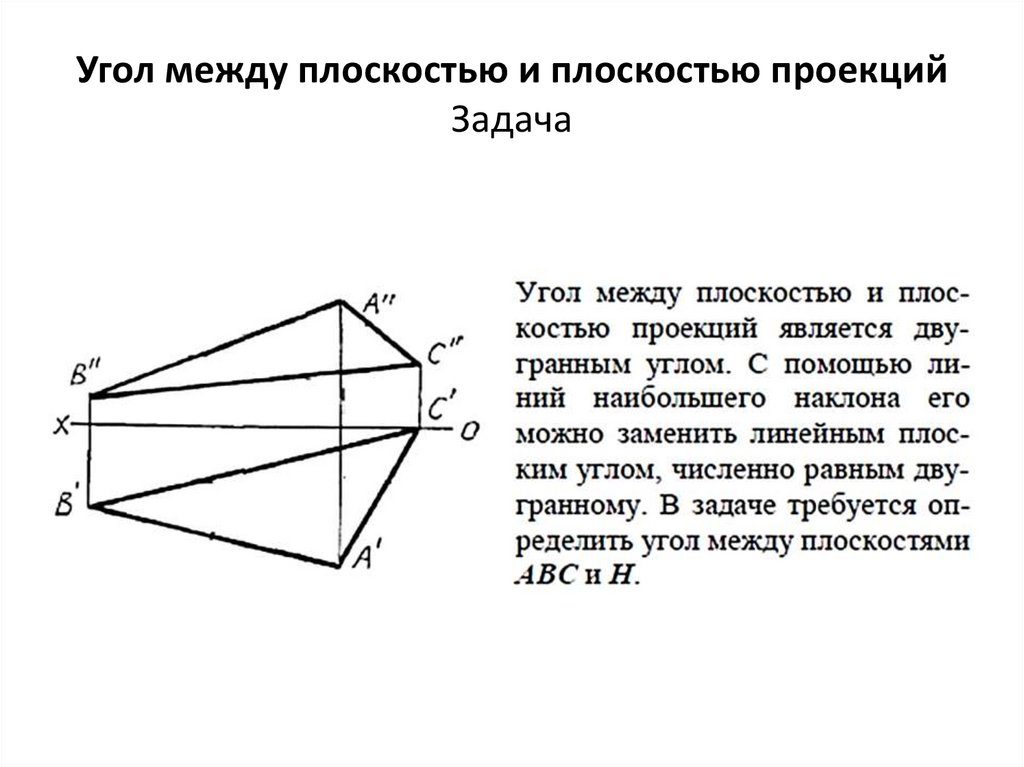
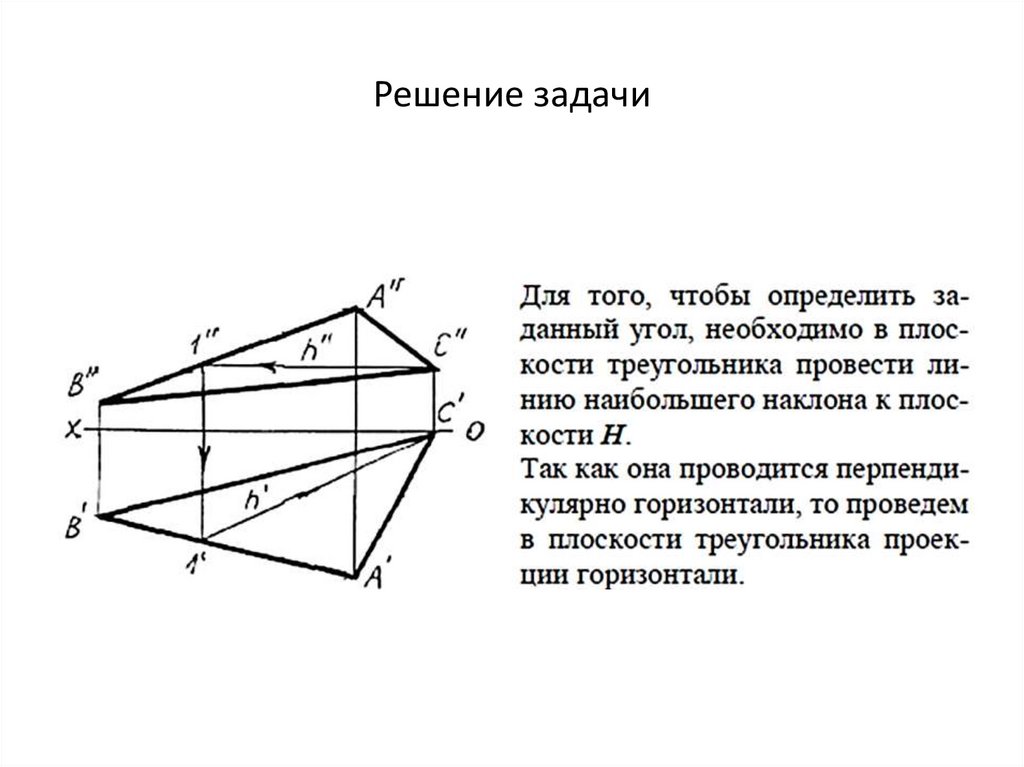
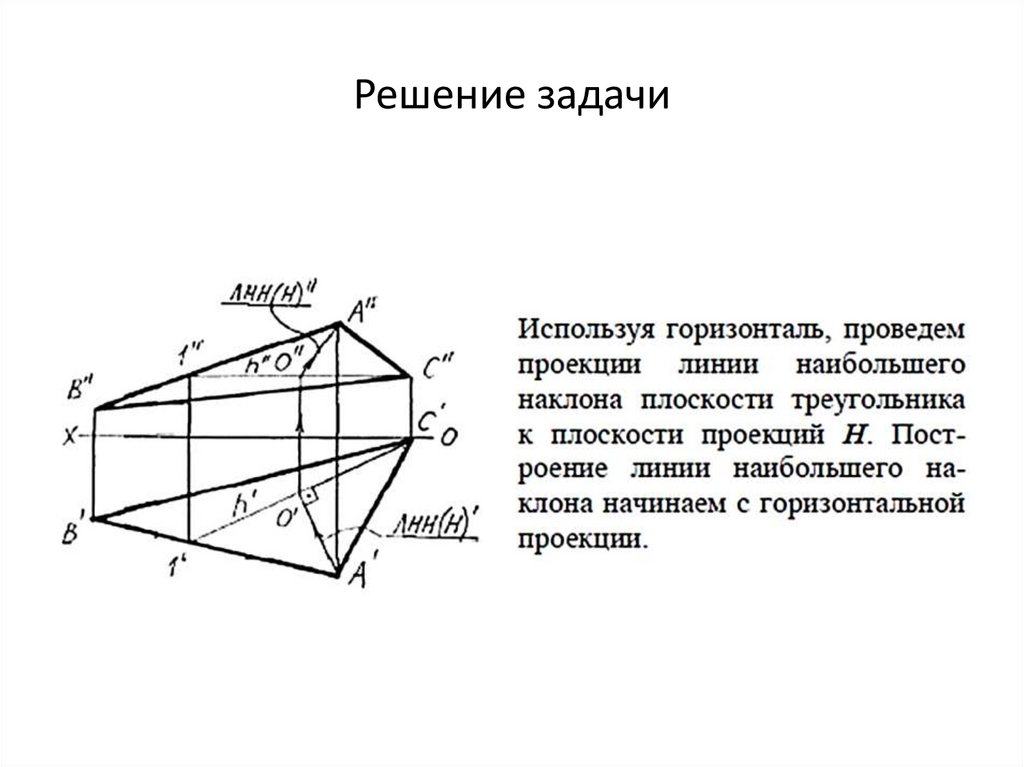
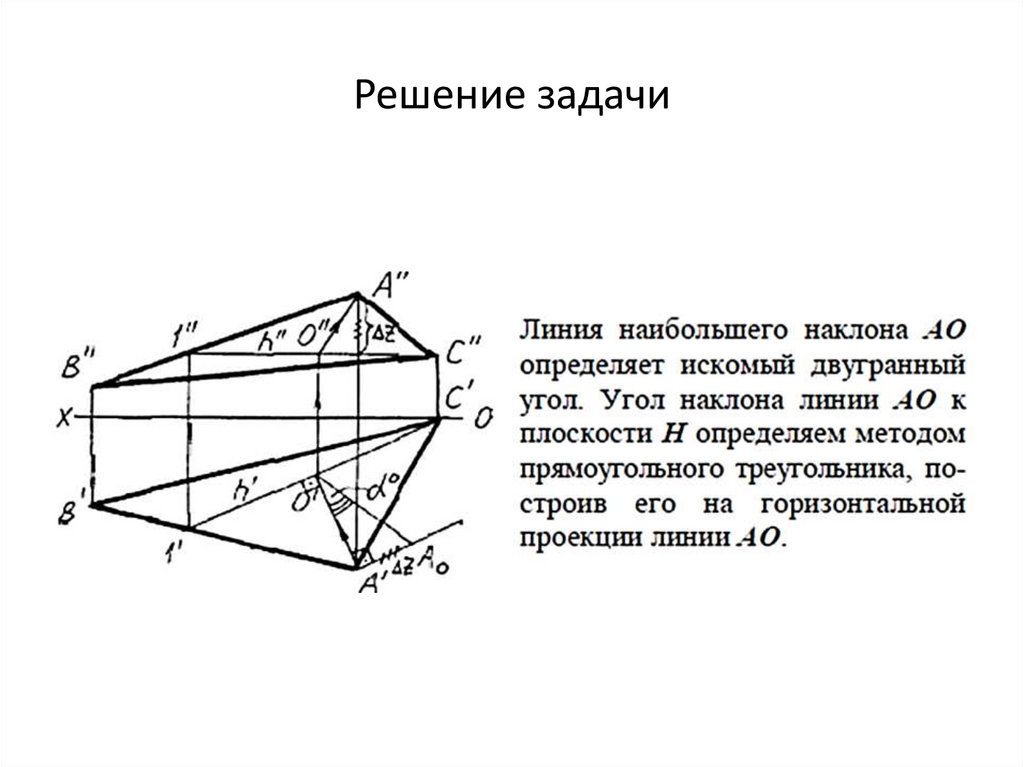
Угол между плоскостью и плоскостью проекцийЗадача






 Инженерная графика
Инженерная графика








