Похожие презентации:
Решение обыкновенных дифференциальных уравнений (тема 8)
1. Тема 8 Решение обыкновенных дифференциальных уравнений
«Вычислительная математика»Тема 8
Решение обыкновенных
дифференциальных
уравнений
1. Метод Эйлера (метод Рунге-Кутта 1-го порядка).
2. Модифицированный метод Эйлера (метод Рунге-Кутта 2-го порядка).
3. Исправленный метод Эйлера.
4. Метод Рунге-Кутта 4 порядка
5. Решение обыкновенных дифференциальных уравнений высших порядков.
2.
Общий вид дифференциального уравнения:F(x, y, y , y ,..., y(n) ) 0
Общее решение ОДУ:
y y(x, C1, C2 ,..., Cn )
Задача решения ОДУ 1-го порядка (задача Коши):
Найти y = y(x), удовлетворяющую уравнению
y’ = f(x,y)
для x0 [a,b] при заданном начальном условии y(x0) = y0.
2
3.
1. Метод Эйлера (метод Рунге-Кутта 1-го порядка).y i
y i y i 1 y i y i 1 y i
x i x i 1 x i
h
y i 1 y i
f(x i , y i )
h
Формула Эйлера:
yi 1 yi h f(x i , yi )
xi a i h
i 0,1,..., n - 1– номер узла
3
4.
y (x 0 ) f(x 0 , y 0 ) tg 0y
y1 = y0 + BC =
y0 + h*tg 0 =
y0 + h*f(x0,y0)
y2
B
y1
D
А
y0
0
h
y=y(x)
C
0
x
0
a=x0
x1
x2
b=xn
M O(h 2 )
max | y in y i2 n |
i 1, n
4
5.
2. Модифицированный метод Эйлера (метод Рунге-Кутта 2-го порядка).L1
y
_
y1
y1
y0
B
L3
А
у=у(х)
h/2
0
L2
h/2
x
x0
А- начальная точка.
L1- касательная к y(x) в точке А.
L2- касательная к у(х) в середине элементарного отрезка
L3 параллельно L2 через т. А
5
6.
Расчётные формулы:y1 y 0
h
f(x 0 , y 0-)значение функции в середине отрезка [x0,x1].
2
h
y1 y 0 h f(x 0 , y1 ) - значение функции в конце отрезка [x0,x1].
2
Формула модифицированного метода Эйлера:
y i 1 y i h f(x i
h
h
, y i f(x i , y i ))
2
2
где
i = 0, 1, …., n-1 - номер узла;
xi = a + i h - координата узла;
у0 = у(х0) - начальное условие.
О(h3).
6
7.
3. Исправленный метод Эйлера.y i 1 y i h
y i y i 1
h
y i [f(x i , y i ) f(x i 1 , y i 1 )]
2
2
y i 1 y i h f(x i , y i )
,
y i 1 y i
h
f(x i , y i ) f(x i 1 , y i h f(x i , y i ))
2
i 0, n 1
где i = 0, 1, …., n-1 - номер узла;
xi = a + i h - координата узла;
у0 = у(х0) - начальное условие.
М = О(h3).
7
8.
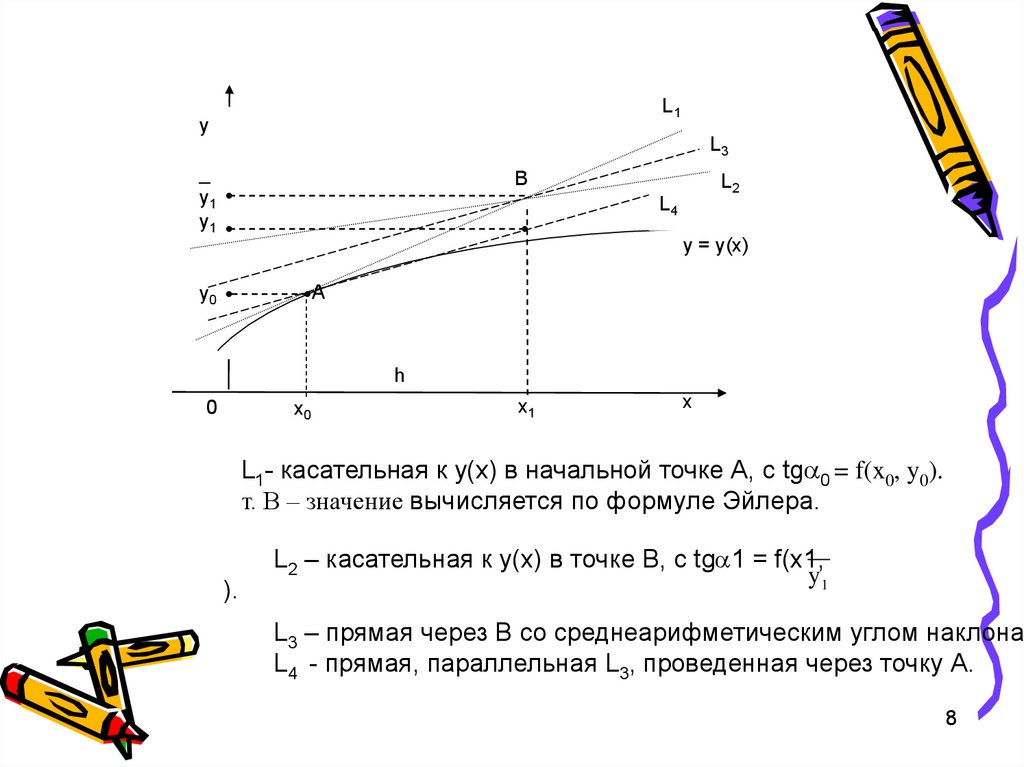
L1y
L3
_
y1
y1
B
L2
L4
y = y(x)
А
y0
h
0
x0
x1
x
L1- касательная к у(х) в начальной точке А, с tg 0 = f(x0, y0).
т. В – значение вычисляется по формуле Эйлера.
).
L2 – касательная к у(х) в точке В, с tg 1 = f(x1,
y1
L3 – прямая через В со среднеарифметическим углом наклона.
L4 - прямая, параллельная L3, проведенная через точку А.
8
9.
4. Метод Рунге-Кутта 4 порядкаРасчетные формулы метода для дифференциального уравнения имеют вид:
y i 1 y i
h
(c 0 2с1 2с 2 с 3 )
6
где i = 0, 1, …., n-1 - номер узла;
xi = a + i h - координата узла;
у0 = у(х0) - начальное условие.
с 0 f(x i , y i )
с
h
с1 f(x i , y i h 0 )
2
2
с
h
с 2 f(x i , y i h 1 )
2
2
с 3 f(x i h, y i h с 2 )
Погрешность метода М = О(h5).
9
10.
5. Решение обыкновенных дифференциальных уравнений высших порядков.Задача Коши для ОДУ n-го порядка:
y (n) f(x, y, y , y ,..., y (n 1) )
с начальными условиями:
y(x0) = y0, y (x0) = y 0, y (x0) = y 0,…, y(n-1)(x0) = y0(n-1).
Обозначим:
y y1
y y 2
,…,
y (n 1) y n 1
y y1
y1 y.2
...
y n 2 y n 1
y n 1 f(x, y, y1 , y 2 ,..., y n 1 )
С начальными условиями:y(x 0 ) y 0
y 2 (x 0 ) y 0
y1 (x 0 ) y 0
,…,
y n -1 (x 0 ) y (n0 -1) 10









 Математика
Математика








