Системы обыкновенных дифференциальных уравнений

1. Решение систем обыкновенных дифференциальных уравнений

Рассмотрим систему из двух дифференциальных
уравнений 1-го порядка:
F1 ( x, y, z, y ' , z ' ) 0
F2 ( x, y, z, y ' , z ' ) 0
Оба уравнения необходимо разрешить относительно
старшей производной:
y ' f1 ( x, y, z )
z ' f 2 ( x, y , z )
Пусть заданы начальные условия: x0, y0, z0.

2.

Данную систему можно решить любым методом,
применимым для решения единичных ОДУ.
Метод Эйлера:
yi 1 yi h f1 ( xi , yi , zi )
zi 1 zi h f 2 ( xi , yi , zi )
xi 1 xi h
Метод Эйлера-Коши:
~
yi 1 yi h f1 ( xi , yi , zi )
~
z z h f (x , y , z )
i 1
i
2
i
i
i
xi 1 xi h
h
yi 1 yi f1 ( xi , yi , zi ) f1 ( xi 1 , ~
yi 1 , ~
zi 1 )
2
h
zi 1 zi f 2 ( xi , yi , zi ) f 2 ( xi 1 , ~
yi 1 , ~
zi 1 )
2

3.

Метод Рунге-Кутта 4-го порядка:
k1 h f1 ( xi , yi , zi )
l1 h f 2 ( xi , yi , zi )
h
k
l
k 2 h f1 ( xi , yi 1 , zi 1 )
2
2
2
h
k
l
l2 h f 2 ( xi , yi 1 , zi 1 )
2
2
2
h
k
l
k3 h f1 ( xi , yi 2 , zi 2 )
2
2
2
h
k
l
l3 h f 2 ( xi , yi 2 , zi 2 )
2
2
2
k 4 h f1 ( xi h, yi k3 , zi l3 )
l4 h f 2 ( xi h, yi k3 , zi l3 )
1
yi 1 yi (k1 2k 2 2k3 k 4 )
6
1
zi 1 zi (l1 2l2 2l3 l4 )
6

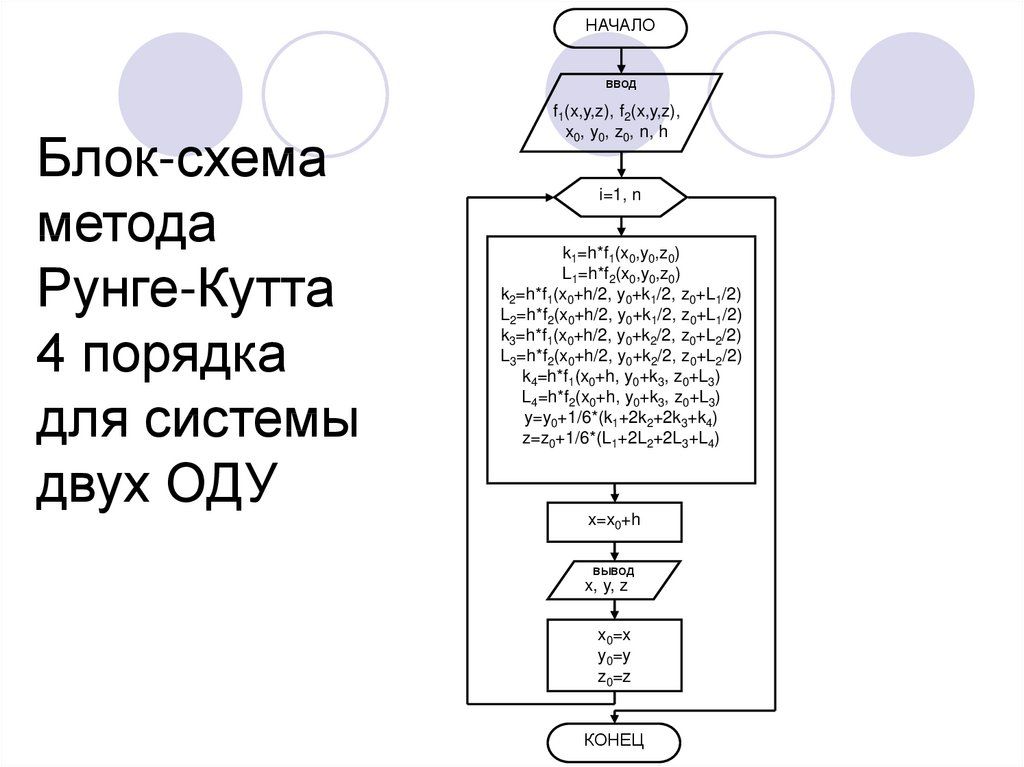
4. Блок-схема метода Рунге-Кутта 4 порядка для системы двух ОДУ

НАЧАЛО
ввод
Блок-схема
метода
Рунге-Кутта
4 порядка
для системы
двух ОДУ
f1(x,y,z), f2(x,y,z),
x0, y0, z0, n, h
i=1, n
k1=h*f1(x0,y0,z0)
L1=h*f2(x0,y0,z0)
k2=h*f1(x0+h/2, y0+k1/2, z0+L1/2)
L2=h*f2(x0+h/2, y0+k1/2, z0+L1/2)
k3=h*f1(x0+h/2, y0+k2/2, z0+L2/2)
L3=h*f2(x0+h/2, y0+k2/2, z0+L2/2)
k4=h*f1(x0+h, y0+k3, z0+L3)
L4=h*f2(x0+h, y0+k3, z0+L3)
y=y0+1/6*(k1+2k2+2k3+k4)
z=z0+1/6*(L1+2L2+2L3+L4)
x=x0+h
вывод
x, y, z
x0=x
y0=y
z0=z
КОНЕЦ

5. Решение обыкновенных дифференциальных уравнений высших порядков

Любое дифференциальное уравнение высшего порядка можно привести
к системе дифференциальных уравнений 1-го порядка путем замены
переменных.
Рассмотрим дифференциальное уравнение 2-го порядка:
F ( x, y, y' , y' ' ) 0
Заданы начальные условия: x0, y0, y’0
Разрешим уравнение относительно старшей производной:
y' ' f ( x, y, y' )
Заменим первую производную y’ функцией z. Тогда y’’=z’, а y’0= z0
Получим систему:
y' z
z ' f ( x, y , z )
Решаем полученную систему известными методами.

6. Пример решения ОДУ 2-го порядка:

2 x 4 y ' ' 3,5 y ' x y 0,
y (2) 4.5,
y ' (2) 3.2
Разрешим уравнение относительно старшей производной :
y'
y
y ' ' 1,75 3 4 . Произведем замену
x 2x
Получим систему :
y' z
z
y
z ' 1,75 x 3 2 x 4
x0 2,
y' z
y0 4.5, z0 3.2