Лекция 9 Поверхности 2го порядка

1.

Математика
Лекция 9

2.

§13 Поверхности второго порядка
Поверхности второго порядка описываются
уравнениями второго порядка относительно
переменных x, y, z.
Среди поверхностей второго порядка выделим
цилиндрические поверхности.

3.

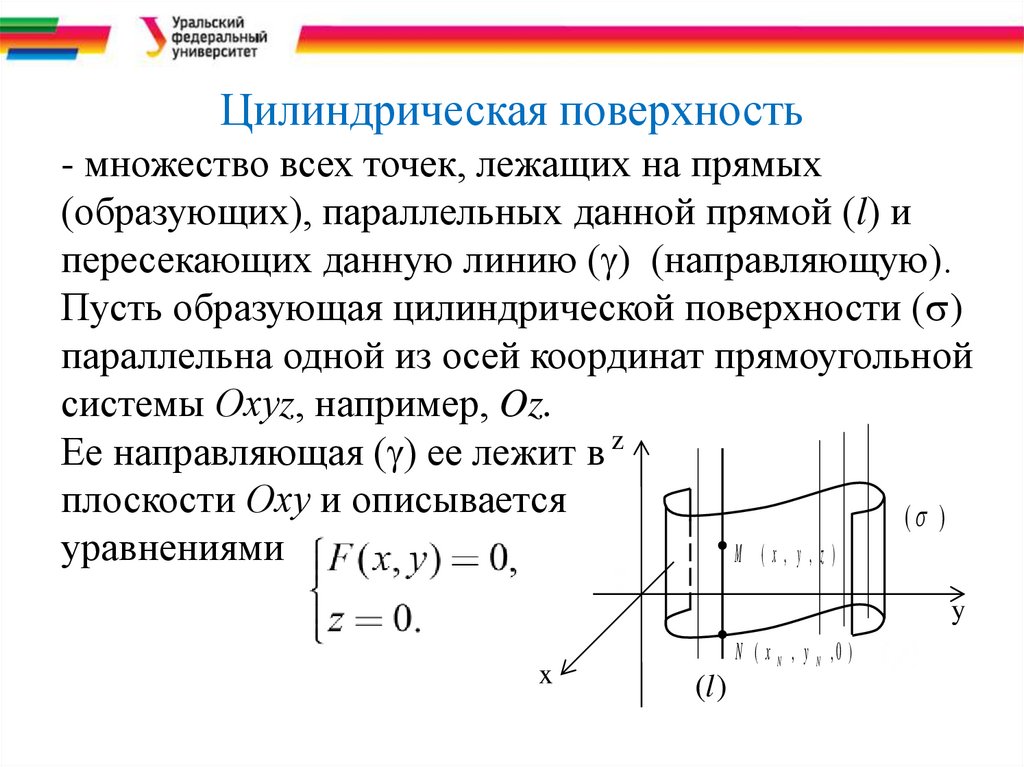
Цилиндрическая поверхность
- множество всех точек, лежащих на прямых
(образующих), параллельных данной прямой (l) и
пересекающих данную линию ( ) (направляющую).
Пусть образующая цилиндрической поверхности ( )
параллельна одной из осей координат прямоугольной
системы Охуz, например, Oz.
Ее направляющая ( ) ее лежит в z
плоскости Оху и описывается
( )
уравнениями
M (x, y,z)
y
x
N ( x N , y N ,0 )
(l )

4.

Аналогично определяются цилиндрические поверхности с
образующими, параллельными оси Ох или Оу.
Замечания
1.Уравнение цилиндрической поверхности, совпадает с
уравнением ее направляющей, расположенной в одной из
координатных плоскостей прямоугольной системы Охуz.
2. Уравнение не содержит одной переменной, одноименной
с осью, параллельной образующей цилиндрической
поверхности.

5.

Пример. y 2 2 px ( p 0)
уравнение цилиндрической поверхности с образующей,
параллельной оси Oz (в уравнении отсутствует
переменная z), с направляющей, расположенной в плоскости
Оху и представляющей параболу с тем же самым
уравнением.
z
y
x

6.

Классификация поверхностей второго порядка
Общее уравнение поверхности 2-го порядка имеет
вид:
где

7.

Теорема.
Общее уравнение поверхности 2-го порядка с
помощью симметрии относительно плоскости,
поворота оси и параллельного переноса
прямоугольной системы координат может быть
приведено к одному из следующих канонических
уравнений:

8.

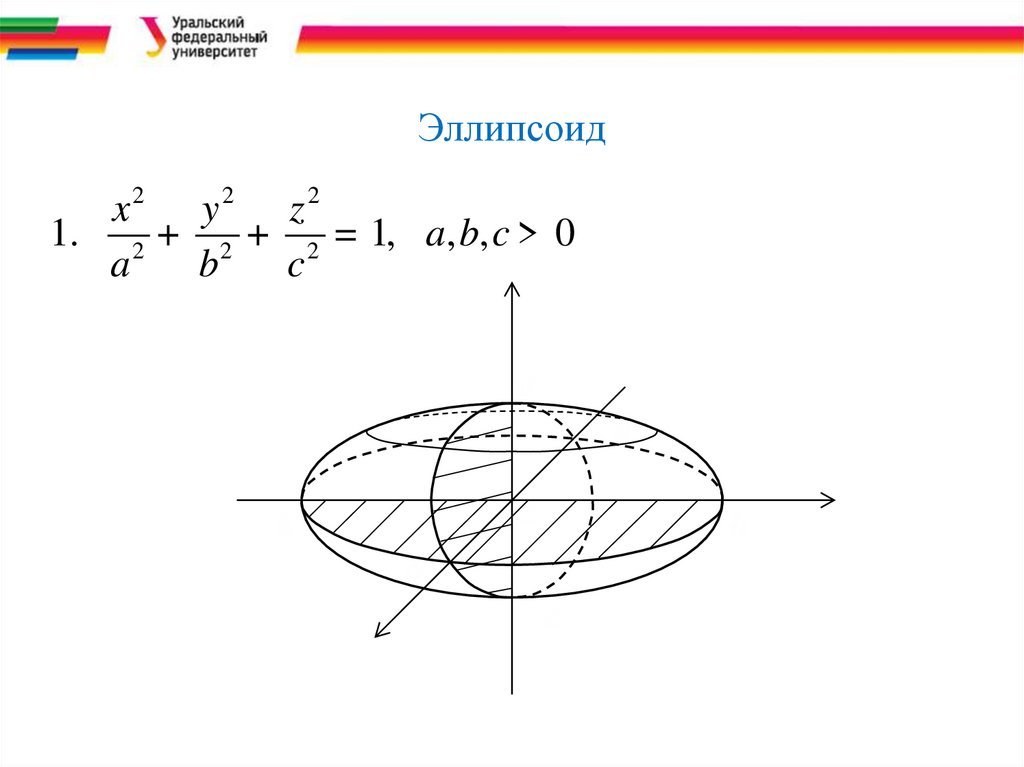
Эллипсоид
x2 y 2 z 2
1. 2 + 2 + 2 = 1, a, b, c > 0
a
b
c

9.

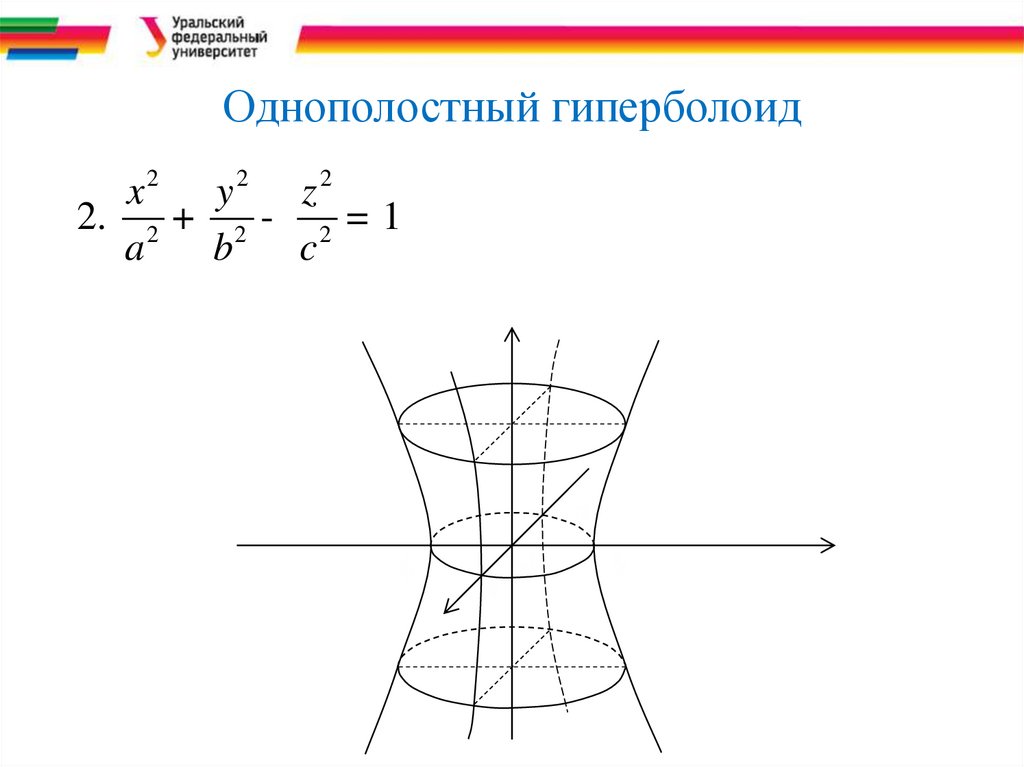
Однополостный гиперболоид
2
2
2
x
y
z
2. 2 + 2 - 2 = 1
a
b
c

10.

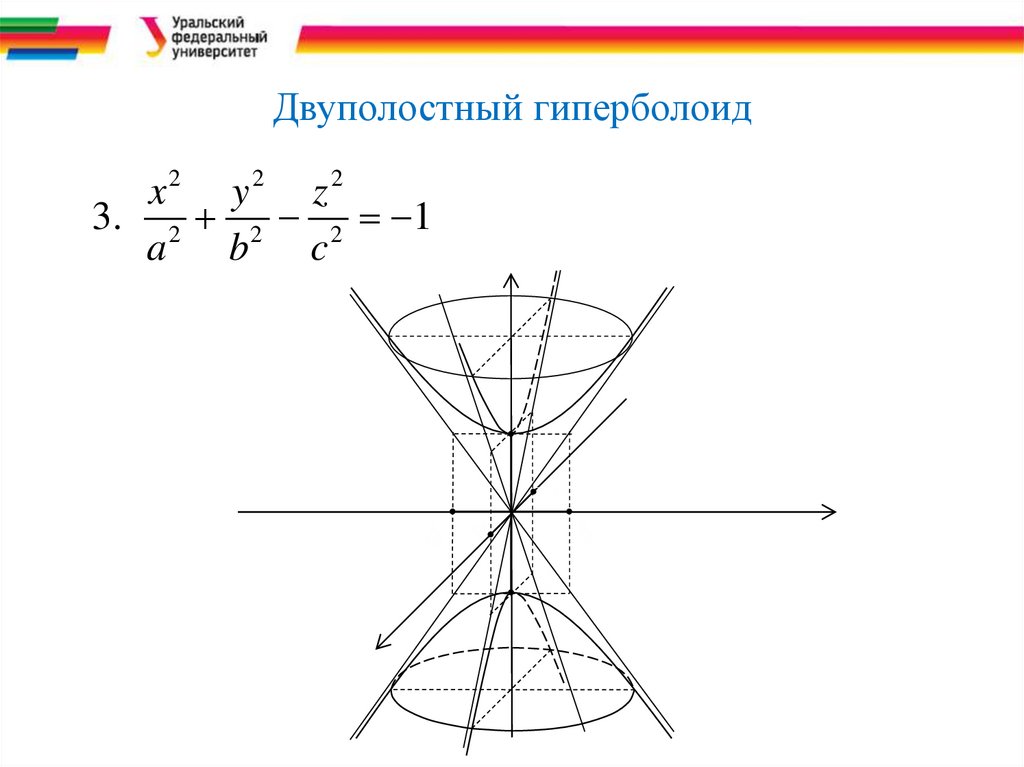
Двуполостный гиперболоид
2
2
2
x
y
z
3. 2 2 2 1
a
b
c

11.

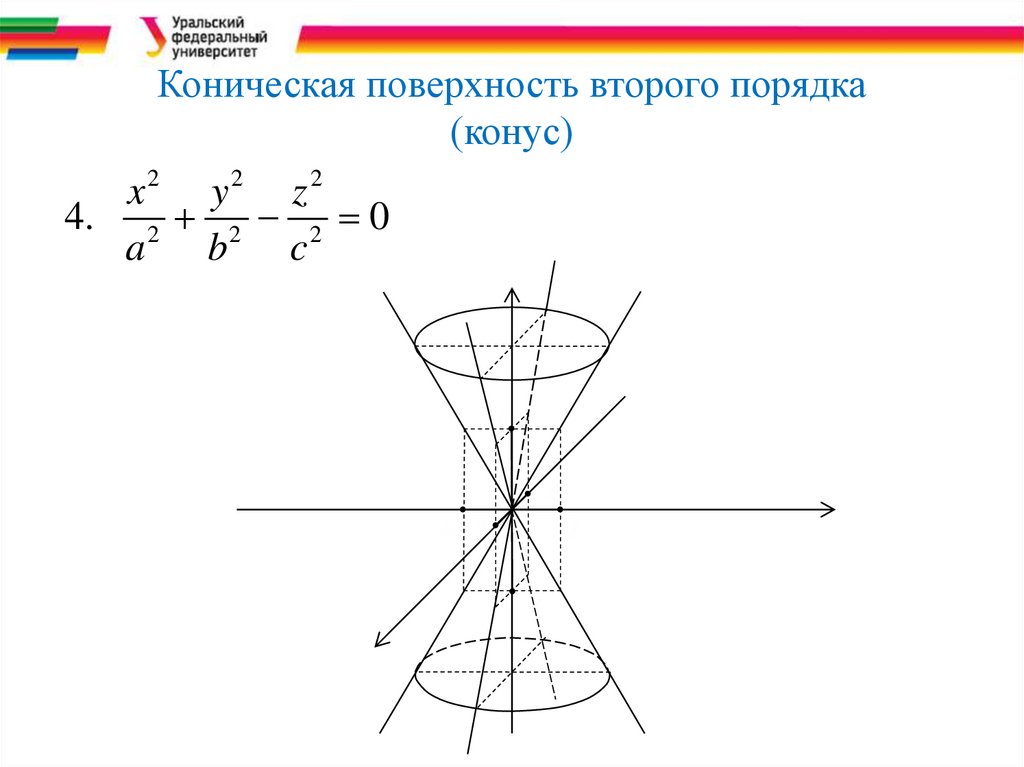
Коническая поверхность второго порядка
(конус)
2
2
2
x
y
z
4. 2 2 2 0
a
b
c

12.

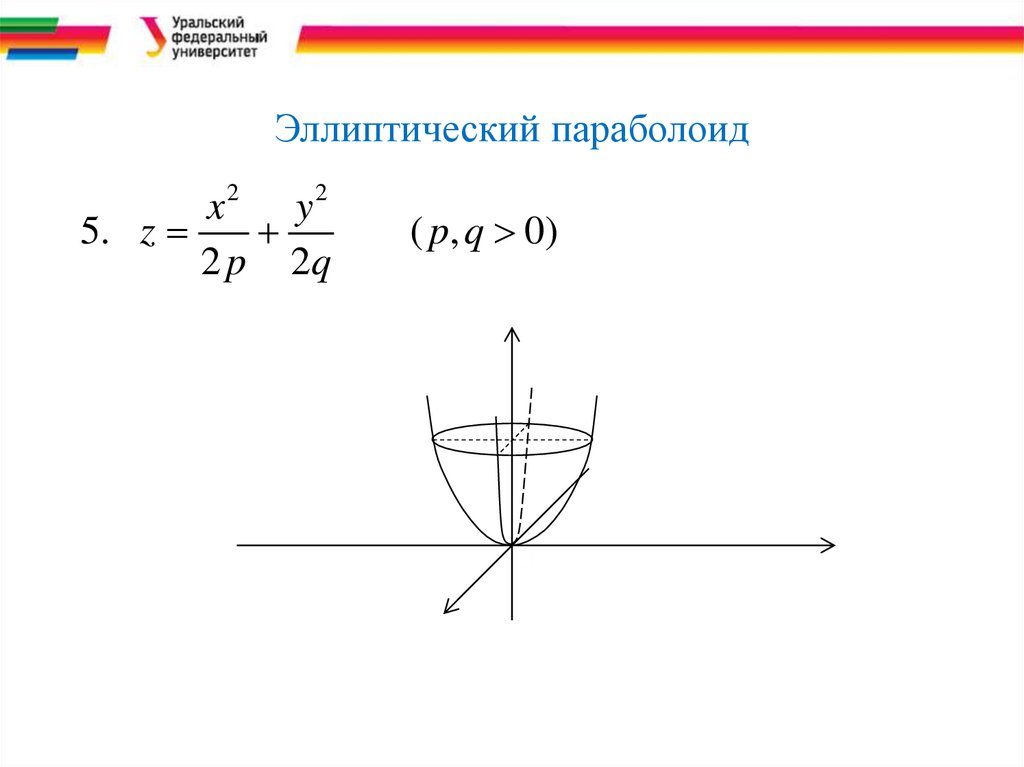
Эллиптический параболоид
x2 y 2
5. z
2 p 2q
( p, q 0)

13.

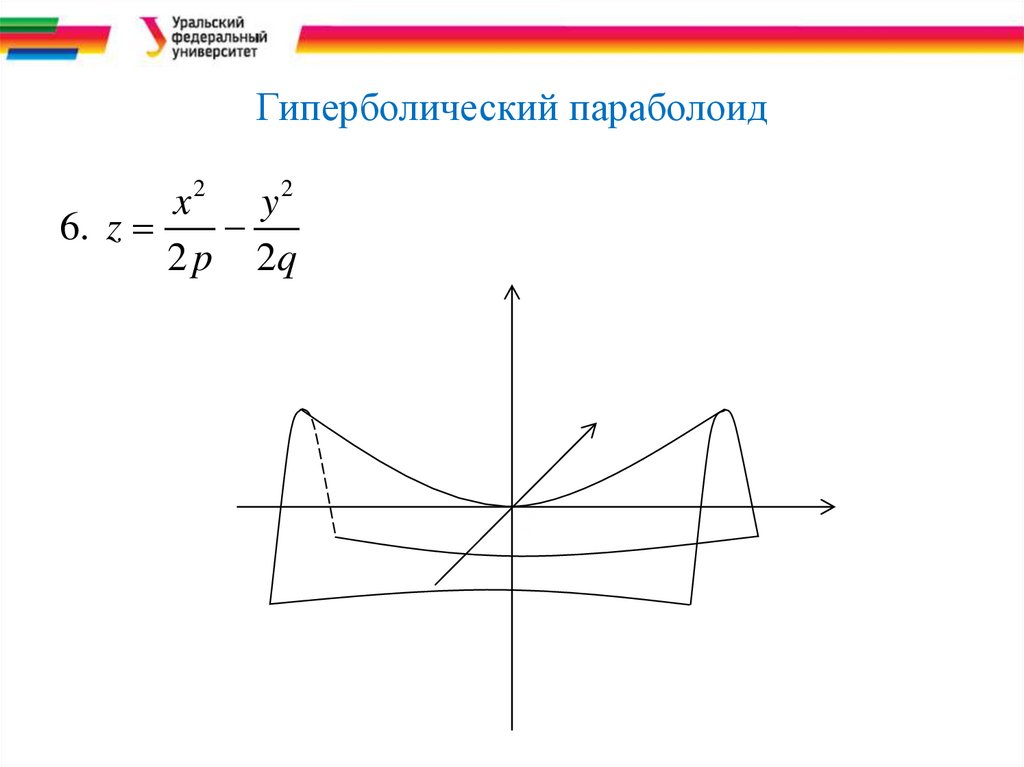
Гиперболический параболоид
x2 y 2
6. z
2 p 2q

14.

7.
x2 y2
2 1 (a,b>0) – эллиптический цилиндр
2
a
b
x2 y2
8. 2 2 1
a
b
- гиперболический цилиндр
9. y 2 2 px ( p 0)
- параболический цилиндр

15.

10.
x2 y2
2 0
2
a
b
- пара пересекающихся плоскостей,
11.
x2 a 2 0
- пара параллельных плоскостей,
12.
x2 0
- пара совпадающих плоскостей,
13.
x2 y2
2 0
2
a
b
- прямая х=у=0 (пара мнимых
пересекающихся плоскостей),

16.

2
2
2
x
y
z
14.
2 2 0 - точка (0, 0, 0) (мнимый конус),
2
a
b
c
x2 y2 z2
15. 2 2 2 1 - (мнимый эллипсоид),
a 2 b2 c
16. x 2 y 2 1 - (мнимый эллиптический цилиндр),
a
b
17. x 2 a 2 0 - (пара мнимых параллельных плоскостей).
Указанное в теореме преобразование системы координат
называется приведением к главным осям.

17.

Метод сечений
Для выяснения формы поверхности в пространстве по ее
уравнению F(x, y, z) = 0 используют метод сечений, который
состоит в анализе пересечений поверхности с плоскостями,
параллельными координатным плоскостям.
F ( x, y, z ) 0,
Например, система
z c,
где параметр с пробегает все действительные значения, задает
пересечение поверхности с плоскостями, параллельными Оху.
Зная эти пересечения, можно представить форму поверхности.

18.

Построение поверхностей второго порядка
Задача. Привести уравнение к каноническому виду и
построить соответствующую поверхность.
1. x2 + 2x + 2y2 − 4y − z2 = 1.
2. x2 − 2x + y2 + 4y + 2z + 5 = 0.