Похожие презентации:
Пластическое деформирование и пластические свойства горных пород. Тема 16
1. Тема 16. Пластическое деформирование и пластические свойства горных пород
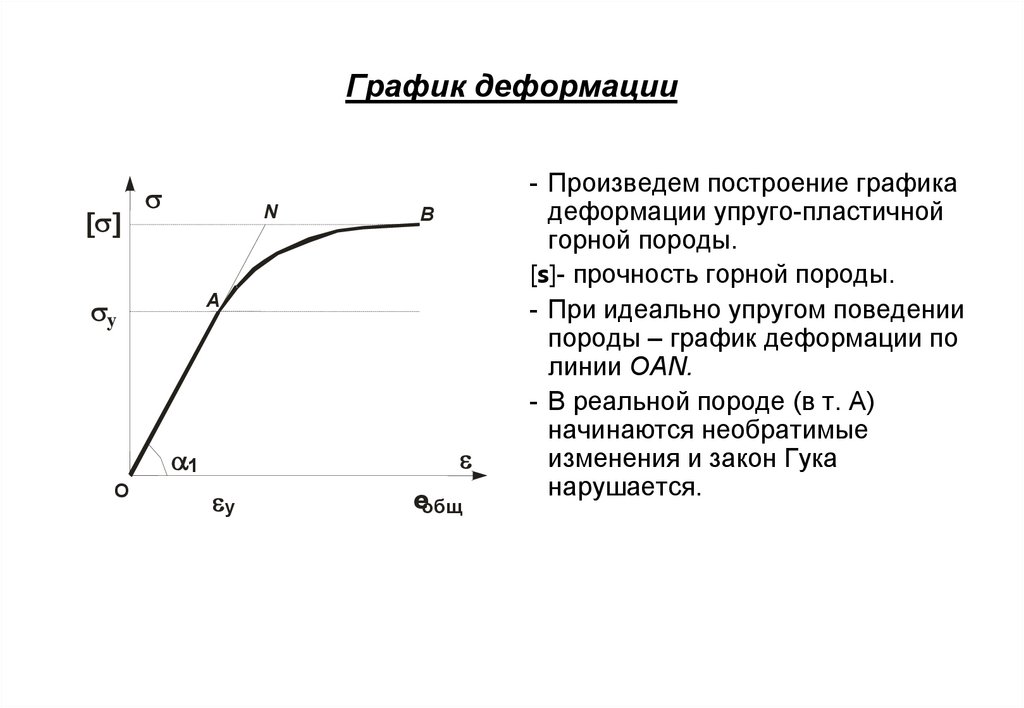
2. График деформации
[s]s
N
A
sy
e
a1
O
B
ey
eобщ
- Произведем построение графика
деформации упруго-пластичной
горной породы.
[s]- прочность горной породы.
- При идеально упругом поведении
породы – график деформации по
линии OAN.
- В реальной породе (в т. А)
начинаются необратимые
изменения и закон Гука
нарушается.
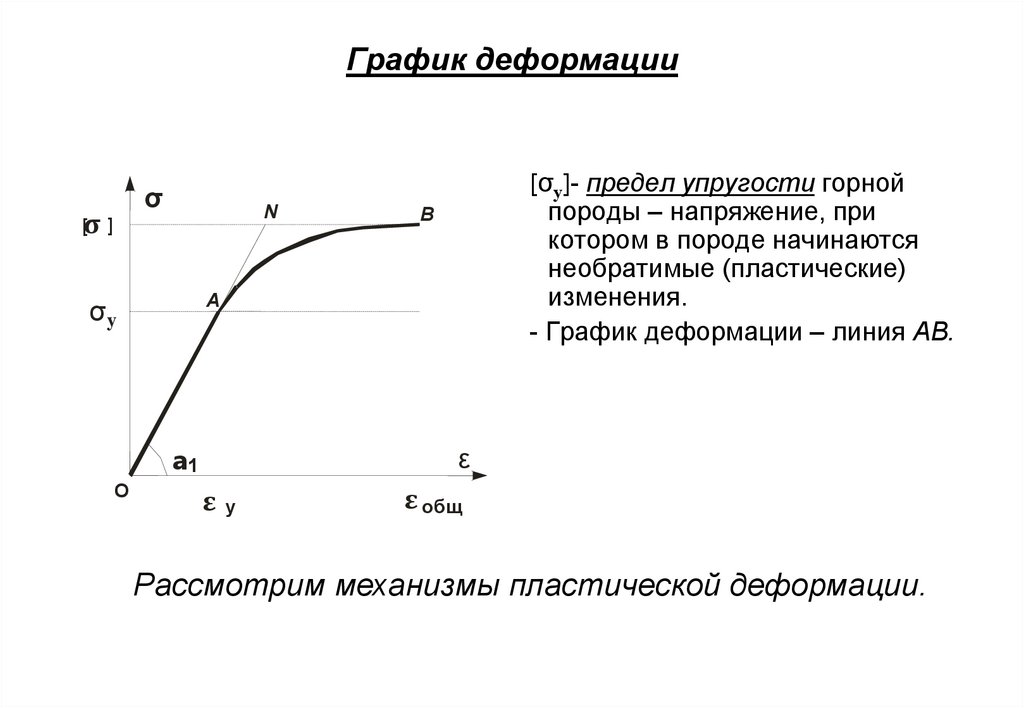
3. График деформации
σ[σ ]
N
B
A
σy
a1
O
[σу]- предел упругости горной
породы – напряжение, при
котором в породе начинаются
необратимые (пластические)
изменения.
- График деформации – линия АВ.
ε
εy
ε общ
Рассмотрим механизмы пластической деформации.
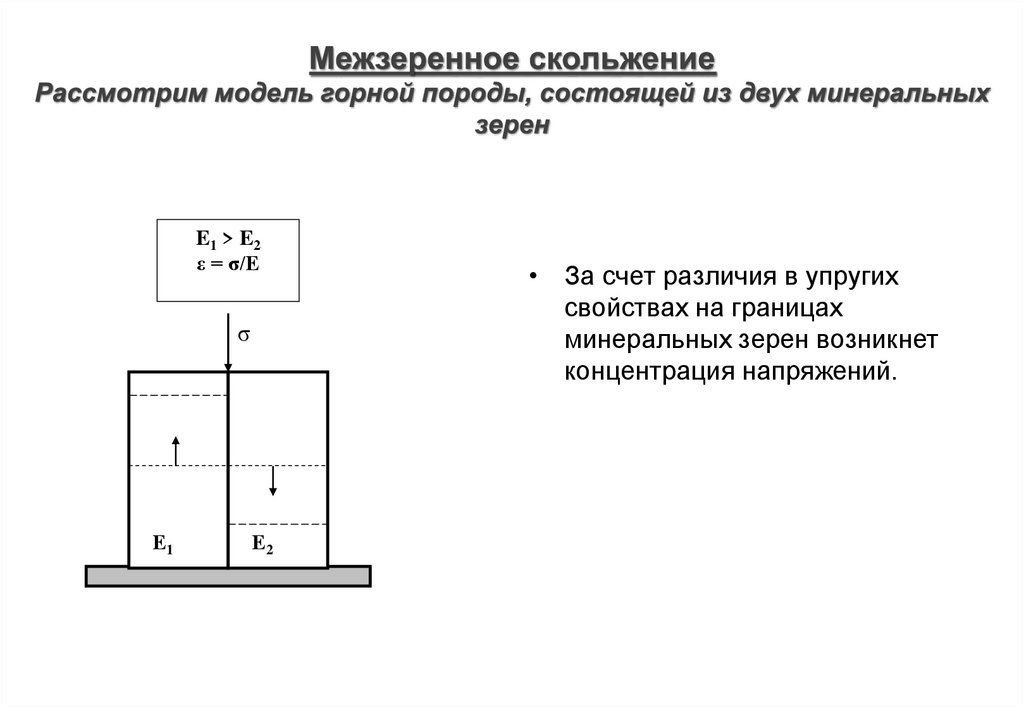
4. Межзеренное скольжение Рассмотрим модель горной породы, состоящей из двух минеральных зерен
E1 > E2ε = σ/E
σ
Е1
Е2
• За счет различия в упругих
свойствах на границах
минеральных зерен возникнет
концентрация напряжений.
5. 1. Межзеренное скольжение Рассмотрим модель горной породы, состоящей из двух минеральных зерен
Если эти напряжения превысят прочность контактапроизойдет его разрушение и необратимое проскальзывание зерен.
E1 > E2
ε = σ/E
σ
σ
Е1
Е2
Е1
Е2
6. Внутрикристаллическое скольжение
σεпл
Обусловлено сдвигом частей
кристалла по плоскостям
ослабления за счет
касательных напряжений.
t
Разрыв межатомных связей по всей плоскости
ослабления требует напряжений = G/30,
где G – модуль сдвига.
Это на несколько порядков выше, чем в реальности.
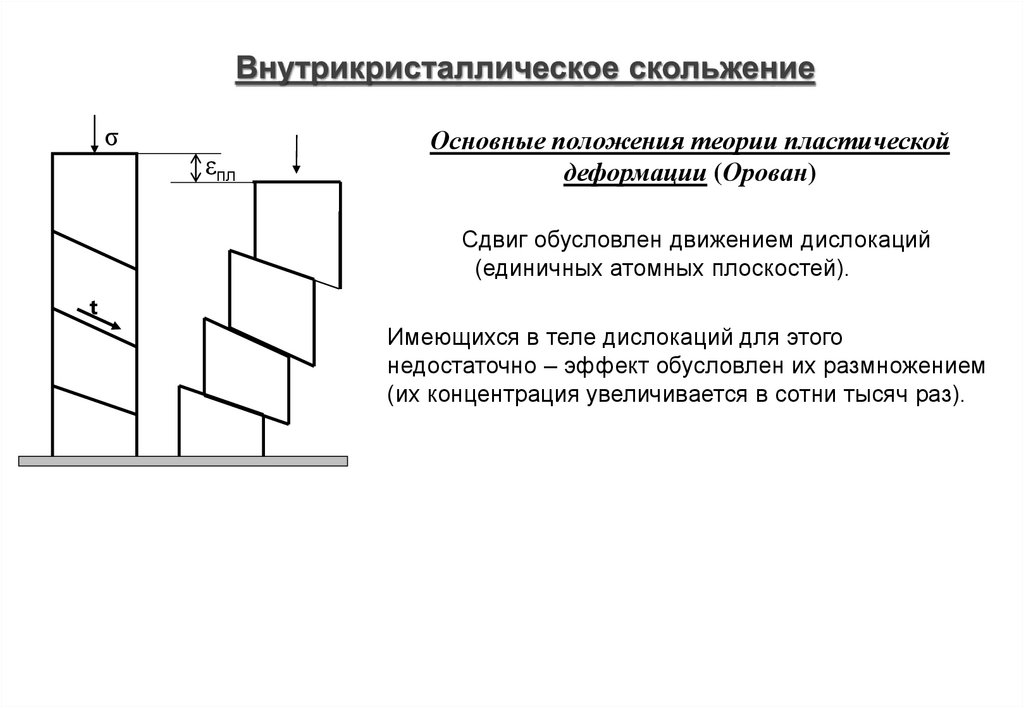
7. Внутрикристаллическое скольжение
σεпл
Основные положения теории пластической
деформации (Орован)
Сдвиг обусловлен движением дислокаций
(единичных атомных плоскостей).
t
Имеющихся в теле дислокаций для этого
недостаточно – эффект обусловлен их размножением
(их концентрация увеличивается в сотни тысяч раз).
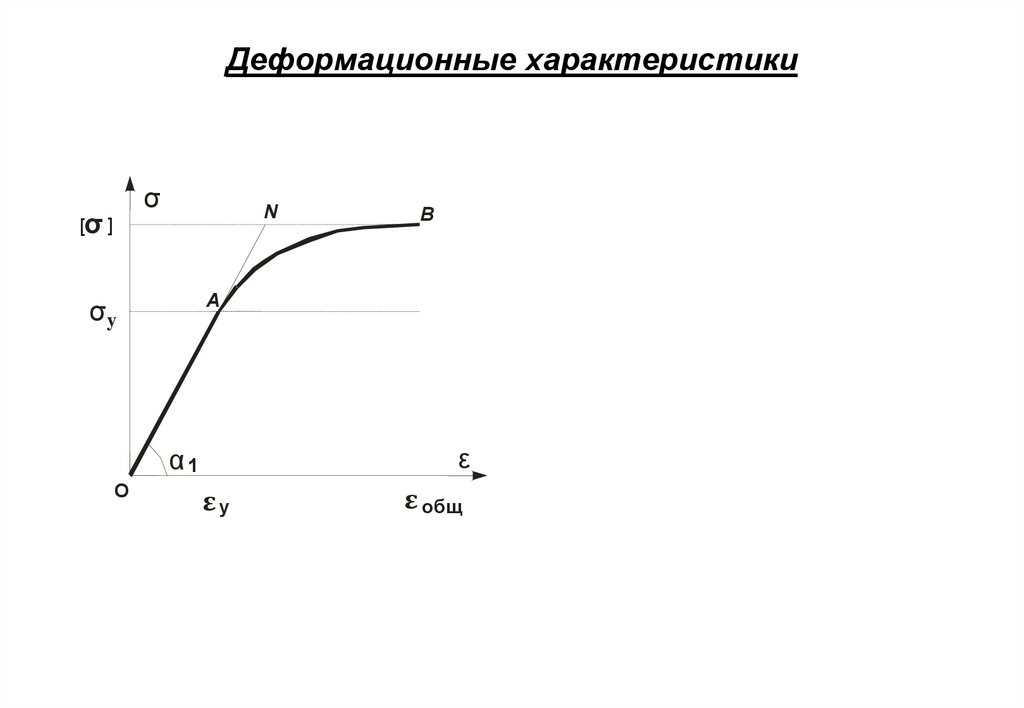
8. Деформационные характеристики
σ[σ ]
N
A
σy
ε
α1
O
B
εy
ε общ
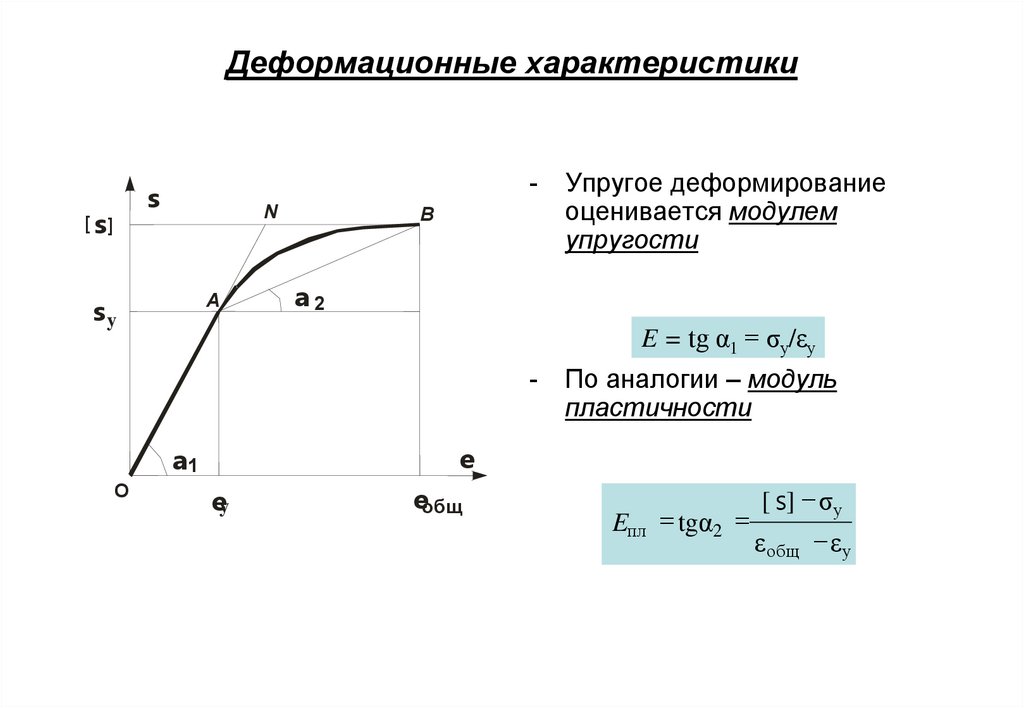
9. Деформационные характеристики
-s
[ s]
N
A
sy
B
a2
E = tg α1 = σу/εу
-
По аналогии – модуль
пластичности
e
a1
O
Упругое деформирование
оценивается модулем
упругости
ey
eобщ
[ s] - σ у
Eпл = tgα2 =
ε общ - ε у
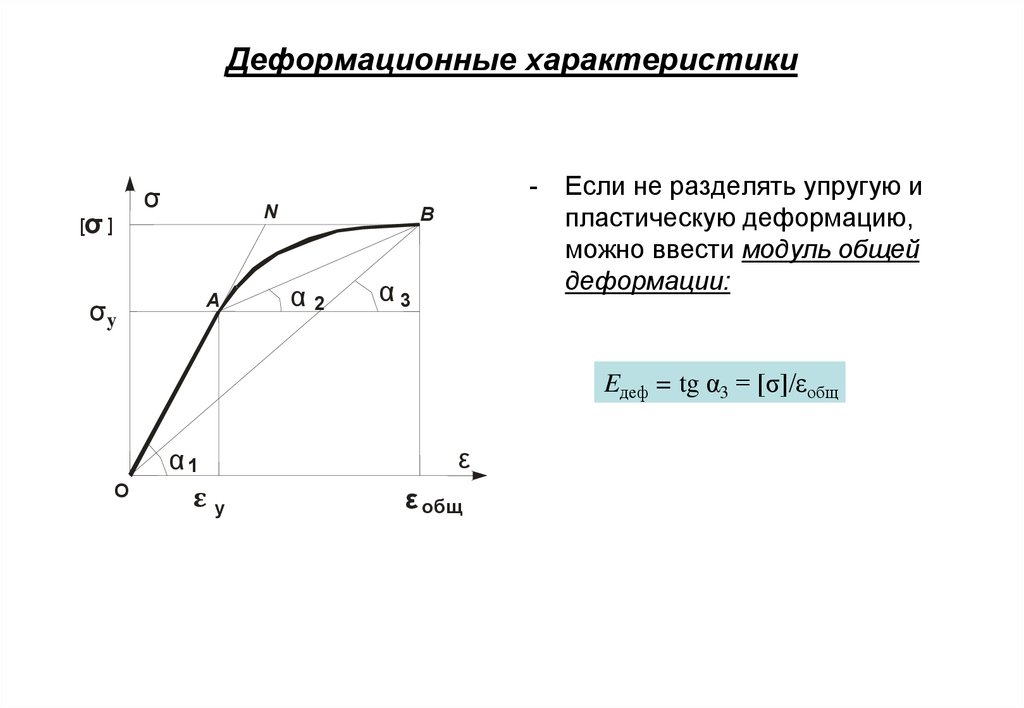
10. Деформационные характеристики
-σ
[σ ]
σy
N
A
B
α2
α3
Если не разделять упругую и
пластическую деформацию,
можно ввести модуль общей
деформации:
Eдеф = tg α3 = [σ]/εобщ
O
α1
εу
ε
ε общ
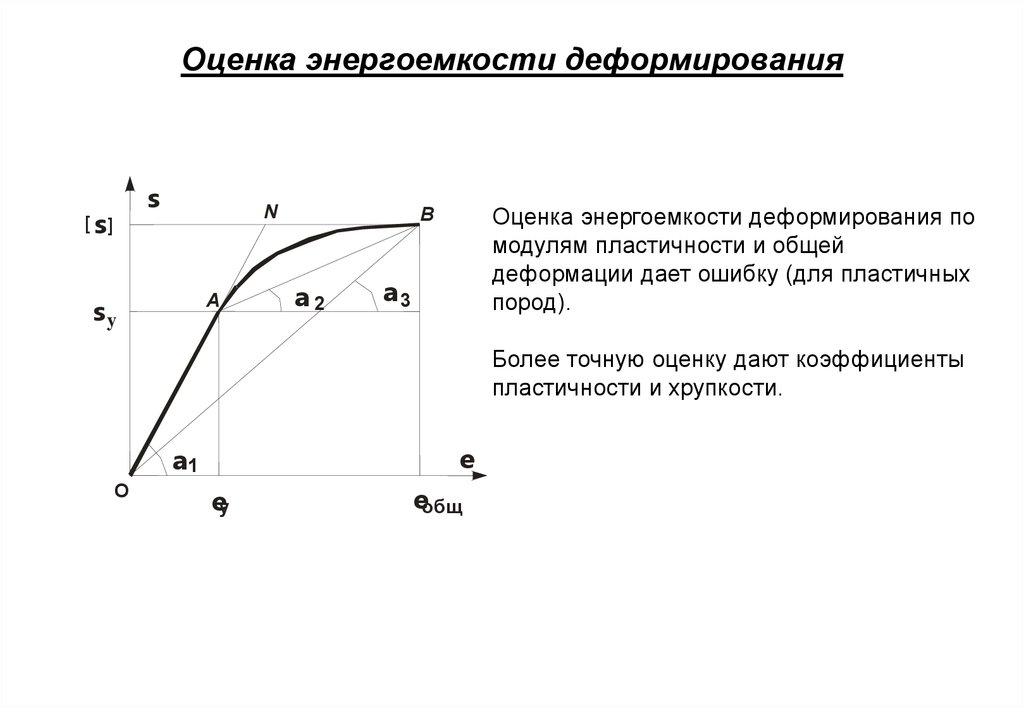
11. Оценка энергоемкости деформирования
s[ s]
N
A
sy
Оценка энергоемкости деформирования по
модулям пластичности и общей
деформации дает ошибку (для пластичных
пород).
B
a2
a3
Более точную оценку дают коэффициенты
пластичности и хрупкости.
e
a1
O
ey
eобщ
12. Коэффициент пластичности
σ[σ]
N
B
A
σy
α1
O
Aобщ Пл.
AOABC
k пл = * kпл= = общ
, 1,
*
ПлA
.ONM
Aу
у
D
εy
M
C
ε
ε общ
где Аобщ – общая работа
деформирования реальной
породы;
Ау* - работа
деформирования этой же
породы, если бы она была
идеально упругой.
kпл показывает проигрыш в
энергоемкости разрушения за
счет необходимости совершать
работу по пластическому
деформированию породы.
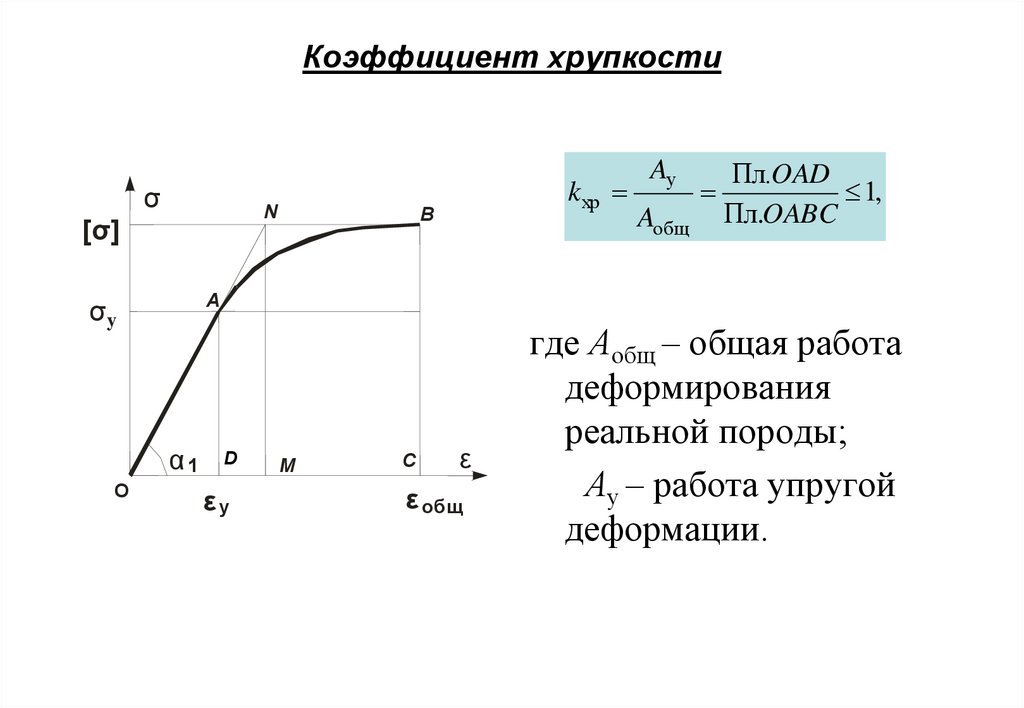
13. Коэффициент хрупкости
σN
[σ]
B
Aобщ
=
Пл.OAD
1,
Пл.OABC
A
σy
α1
O
k хр =
Aу
D
εy
M
C
ε
ε общ
где Аобщ – общая работа
деформирования
реальной породы;
Ау – работа упругой
деформации.





 География
География








