3_Урав_Прям на плоск

1.

Линейная алгебра и аналитическая геометрия
ВИДЫ УРАВНЕНИЙ
ПРЯМОЙ НА ПЛОСКОСТИ

2.

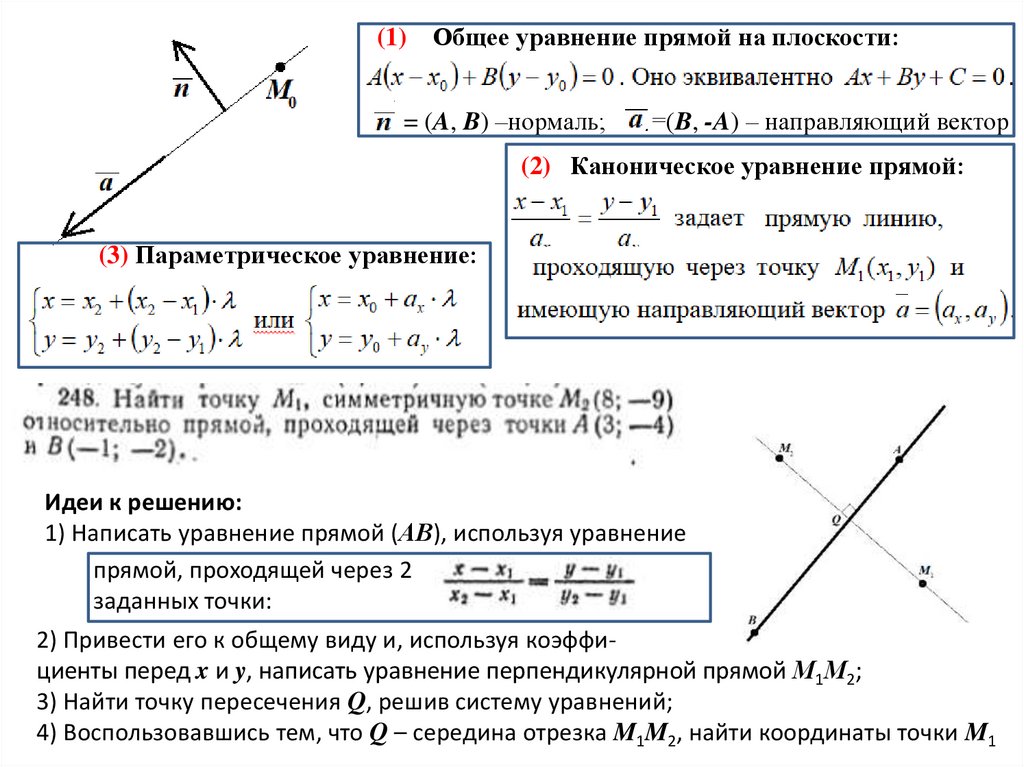
(1)
Общее уравнение прямой на плоскости:
= (A, B) –нормаль;
=(B, -A) – направляющий вектор
(2) Каноническое уравнение прямой:
(3) Параметрическое уравнение:
Идеи к решению:
1) Написать уравнение прямой (АВ), используя уравнение
прямой, проходящей через 2
заданных точки:
2) Привести его к общему виду и, используя коэффициенты перед x и y, написать уравнение перпендикулярной прямой М1М2;
3) Найти точку пересечения Q, решив систему уравнений;
4) Воспользовавшись тем, что Q – середина отрезка M1M2, найти координаты точки M1

3.

(A, B) –нормаль;
(B, -A) – направляющий вектор

4.

(4)
Уравнение прямой, проходящей через 2 точки:

5.

6.

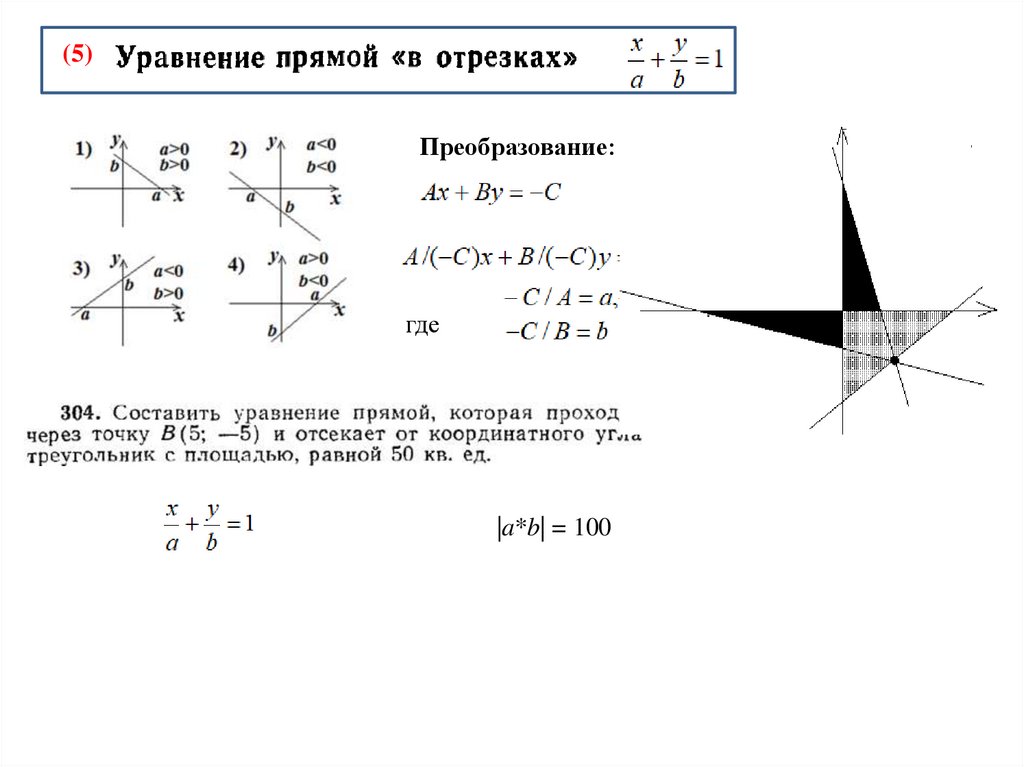
(5)
Преобразование:
где
|a*b| = 100

7.

(6 и 7)
(7)
(6)
уравнение в общем виде :
необходимо домножить на нормирующий множитель:

8.

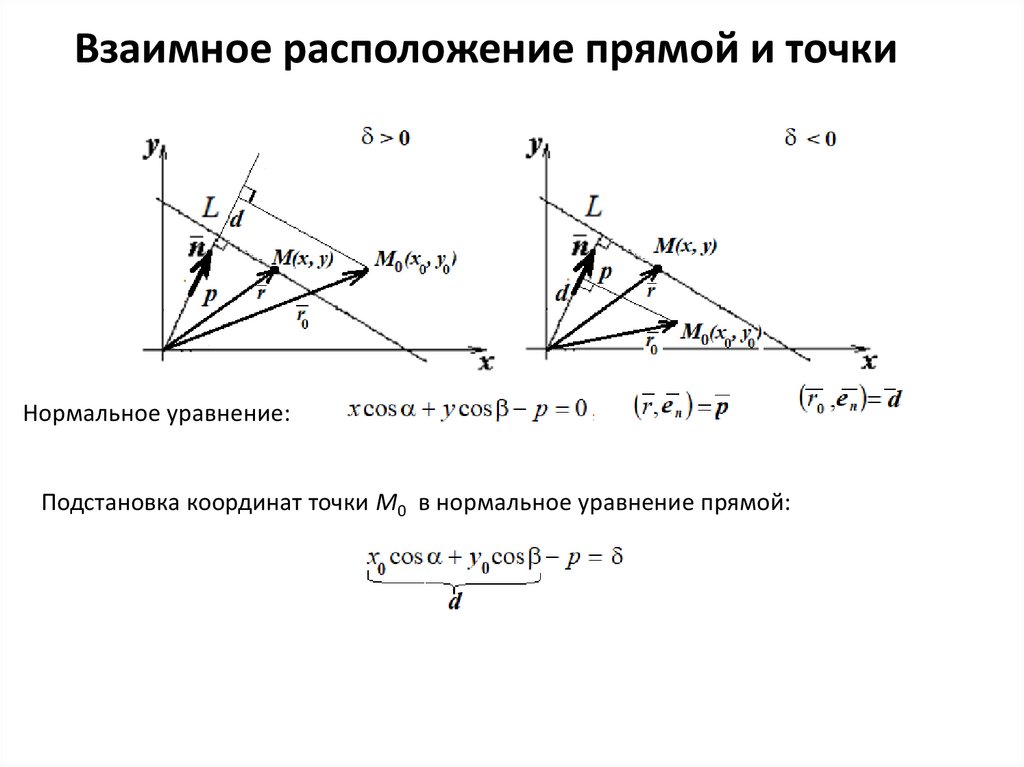
Взаимное расположение прямой и точки
Нормальное уравнение:
Подстановка координат точки М0 в нормальное уравнение прямой:

9.

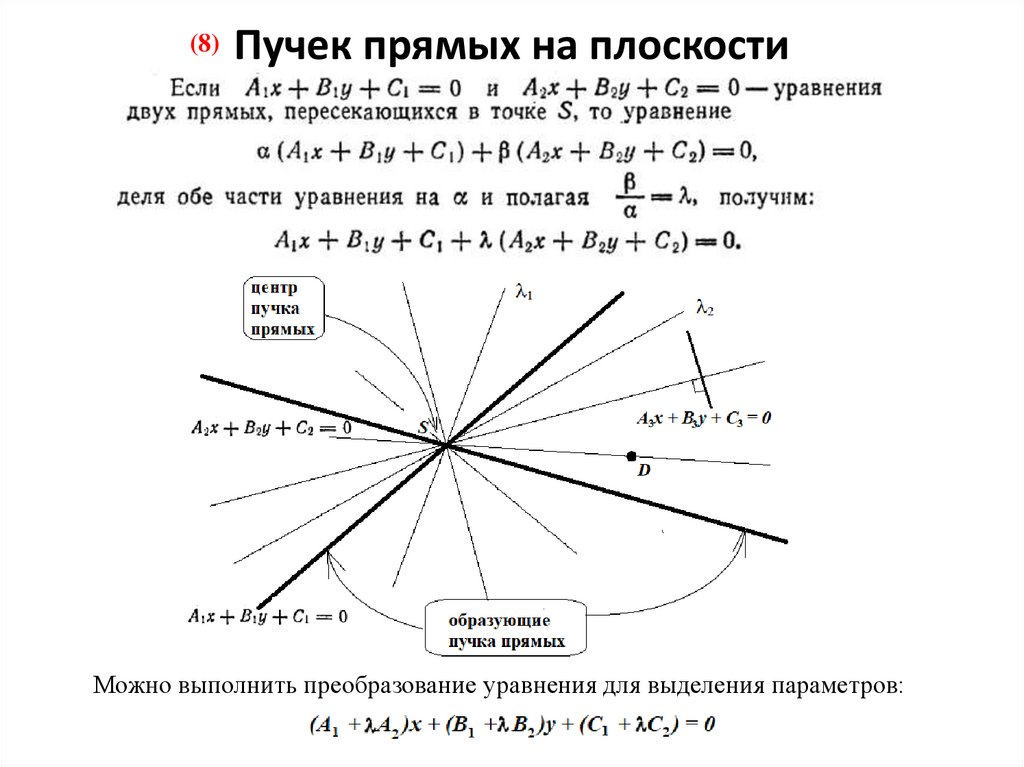
(8)
Пучек прямых на плоскости
Можно выполнить преобразование уравнения для выделения параметров:

10.

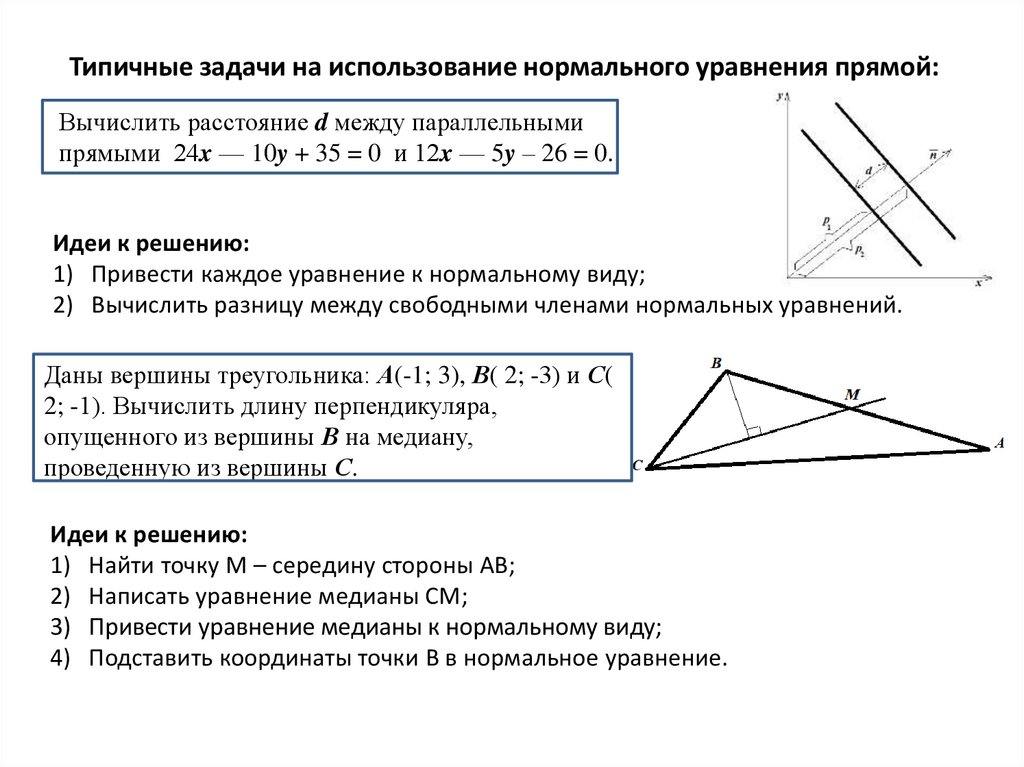
Типичные задачи на использование нормального уравнения прямой:
Вычислить расстояние d между параллельными
прямыми 24x — 10y + 35 = 0 и 12x — 5y – 26 = 0.
Идеи к решению:
1) Привести каждое уравнение к нормальному виду;
2) Вычислить разницу между свободными членами нормальных уравнений.
Даны вершины треугольника: А(-1; 3), В( 2; -3) и С(
2; -1). Вычислить длину перпендикуляра,
опущенного из вершины В на медиану,
проведенную из вершины С.
Идеи к решению:
1) Найти точку М – середину стороны АВ;
2) Написать уравнение медианы СМ;
3) Привести уравнение медианы к нормальному виду;
4) Подставить координаты точки B в нормальное уравнение.

11.

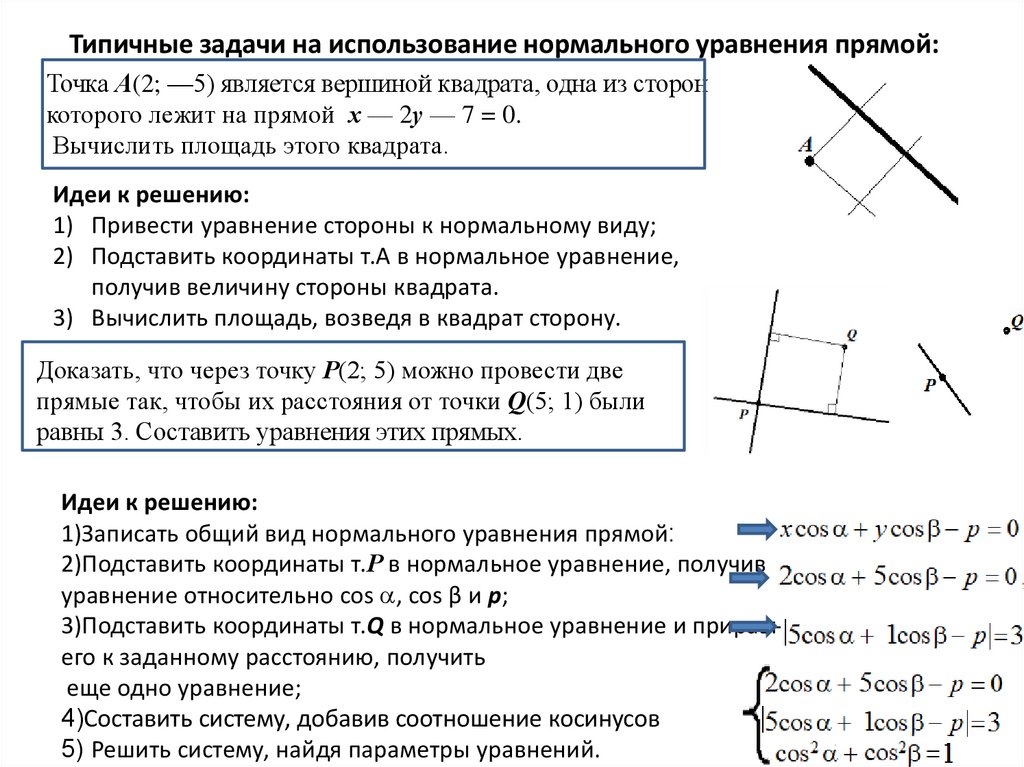
Типичные задачи на использование нормального уравнения прямой:
Точка А(2; —5) является вершиной квадрата, одна из сторон
которого лежит на прямой х — 2у — 7 = 0.
Вычислить площадь этого квадрата.
Идеи к решению:
1) Привести уравнение стороны к нормальному виду;
2) Подставить координаты т.А в нормальное уравнение,
получив величину стороны квадрата.
3) Вычислить площадь, возведя в квадрат сторону.
Доказать, что через точку Р(2; 5) можно провести две
прямые так, чтобы их расстояния от точки Q(5; 1) были
равны 3. Составить уравнения этих прямых.
Идеи к решению:
1)Записать общий вид нормального уравнения прямой:
2)Подставить координаты т.Р в нормальное уравнение, получив
уравнение относительно cos , cos β и p;
3)Подставить координаты т.Q в нормальное уравнение и приравняв
его к заданному расстоянию, получить
еще одно уравнение;
4)Составить систему, добавив соотношение косинусов
5) Решить систему, найдя параметры уравнений.

12.

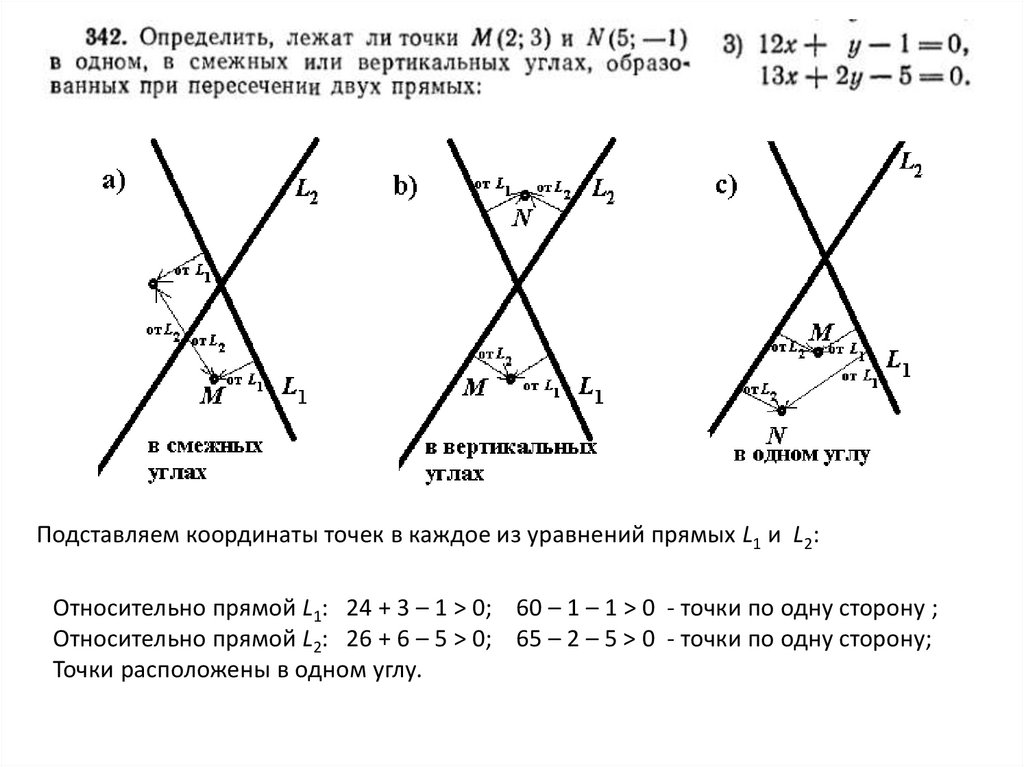
Подставляем координаты точек в каждое из уравнений прямых L1 и L2:
Относительно прямой L1: 24 + 3 – 1 > 0; 60 – 1 – 1 > 0 - точки по одну сторону ;
Относительно прямой L2: 26 + 6 – 5 > 0; 65 – 2 – 5 > 0 - точки по одну сторону;
Точки расположены в одном углу.

13.

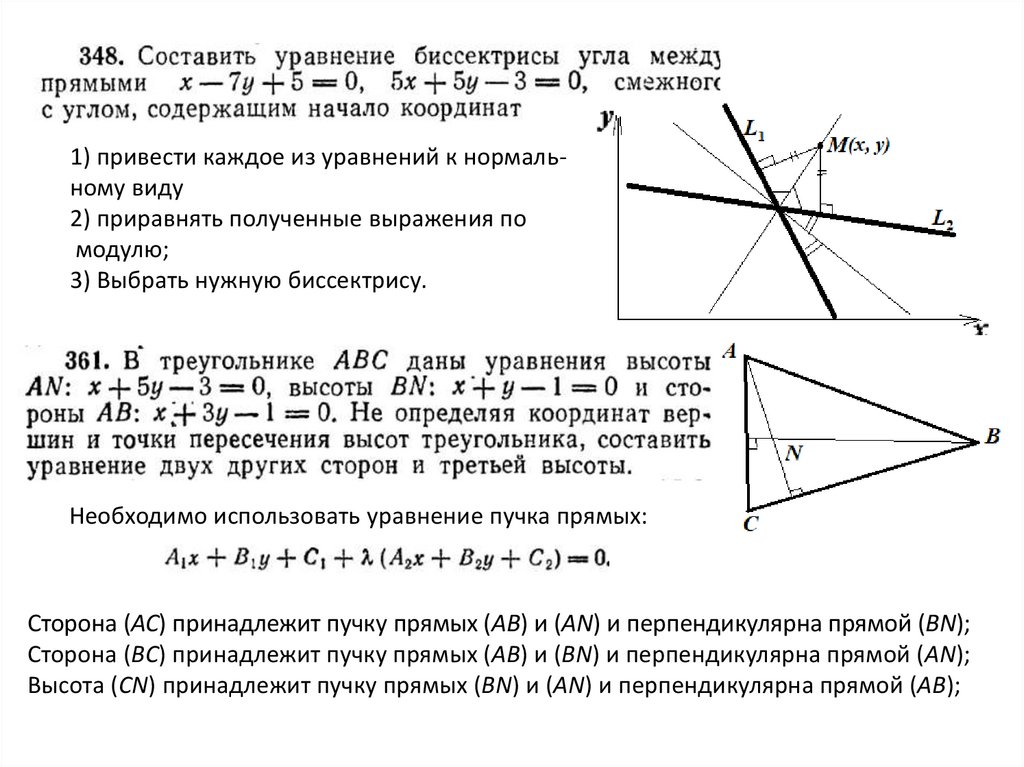
1) привести каждое из уравнений к нормальному виду
2) приравнять полученные выражения по
модулю;
3) Выбрать нужную биссектрису.
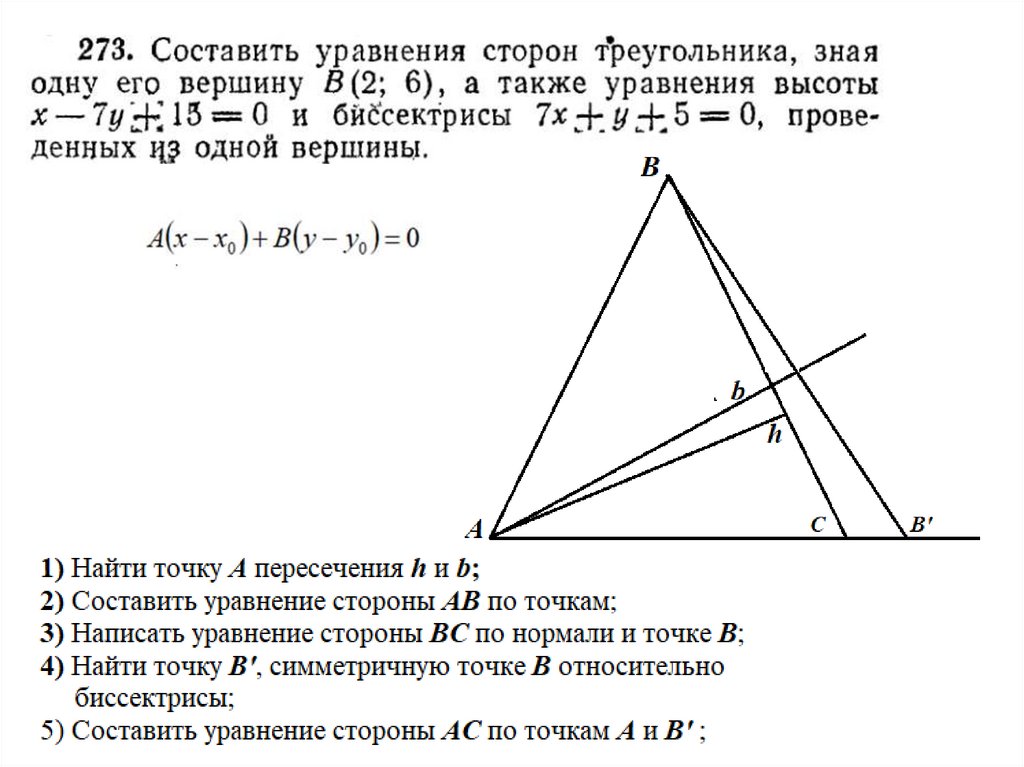
Необходимо использовать уравнение пучка прямых:
Сторона (АС) принадлежит пучку прямых (АВ) и (АN) и перпендикулярна прямой (ВN);
Сторона (ВС) принадлежит пучку прямых (АВ) и (ВN) и перпендикулярна прямой (АN);
Высота (СN) принадлежит пучку прямых (ВN) и (АN) и перпендикулярна прямой (АВ);

14.

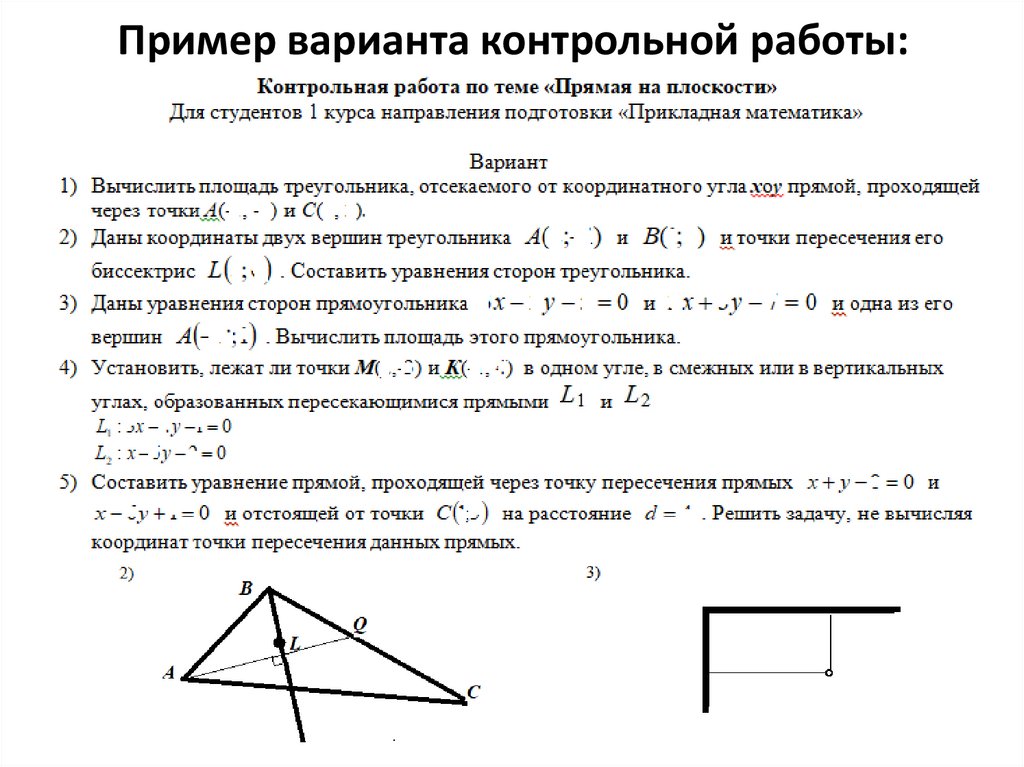
Идеи решения:
Каждая из 2-х смежных сторон квадрата принадлежит пучку!
1) Записать уравнение пучка в виде (2x-3y+20)+ (3x+5y-27)=0 и преобразовать,
вынося за скобки x и y ;
2) Определить коэффициенты А1 и В1 в полученном уравнении. Они будут
зависеть от
3) Воспользовавшись тем, что углы между сторонами квадрата и его
диагональю равны 45 и минус 45 градусов, воспользоваться формулой:
где А2 и В2 – коэффициенты в уравнении диагонали
4) Решить полученное уравнение относительно
5) Подставить найденные значения в уравнение пучка.

15.

1) Запишем общий вид уравнения сторон: A(x - x0) + B(y-y0)=0
2) Преобразуем его к виду, учитывая, что координаты т.А должны ему удовлетворять:
y - 0 = A2(x – 2) или А2x – y - 2 A2 = 0. здесь B2 = -1.
3) Воспользуемся формулой для вычисления угла между прямыми:
4) Поскольку угол может быть равен 60 и минус 60 градусов, то подставим:
5) Решим полученные уравнения относительно А2;
6) Подставим найденные значения в общее уравнение прямых.

16.

Пример варианта контрольной работы: