Похожие презентации:
Решение задач на вычисление расстояния методом координат
1.
Решение задач на вычислениерасстояния методом координат
Учитель математики МАОУ «Лицей № 6»
Юдина Елена Павловна
2.
14. Стереометрическая задачаРасстояние между прямыми и плоскостями
Расстояние от точки до прямой и до плоскости
Сечения многогранников
Угол между плоскостями
Угол между прямой и плоскостью
Угол между скрещивающимися прямыми
Объёмы многогранников
Круглые тела: цилиндр, конус, шар
3.
Координаты вектора
Длина вектора
Скалярное произведение векторов
Скалярное произведение векторов в координатах
Свойство скалярного произведения взаимно
перпендикулярных векторов
• Свойство координат коллинеарных векторов
• Угол между векторами
4.
Задача на нахождение расстояние от точки до прямойЗадача 511106
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой
равны 4, точка N — середина ребра AC, точка O - центр основания пирамиды,
точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
S
4
Р
N
А
О
4
В
Дано:
SABC – правильная пирамида, рёбра которой равны 4,
точка N — середина AC, точка O - центр основания,
точка P SO, SР : РО = 3 : 1.
а) Доказать: NP BS.
б) Найти: расстояние от точки B до прямой NP.
С Решение:
5.
Задача 511106z
1) Введём прямоугольную систему координат.
Найдём координаты точек А, В, С, S, О, Р и N.
2) Координаты точек:
А(0;0;0),
С(0;4;0), (т.к. АС = 4),
N(0;2;0), (т.к. АN = 2)
S
4
Р
N
А
О
4
х
В
4 у
С
3) Координаты точки В:
6.
Задача 511106N
2
А
у
С
4
х
О
В
2) Координаты точек:
А(0;0;0), С(0;4;0), N(0;2;0)
3) Координаты точки В:
ВN – медиана и высота АВС.
Рассмотрим АВN: N = 900, АN = 2, АВ = 4,
по теореме Пифагора ВN = 16 4 2 3 .
В ( 2 3;2;0)
4) Координаты точки О:
1
2
О – центр АВС, тогда ВО:ОN = 2:1, т.е. ОN = ВN =
3
2 3
О(
;2;0)
3
5) Координаты точки S:
3
3
7.
Задача 511106z
5) Координаты точки S:
S
SО – высота правильной пирамиды, SО (АВС),
тогда SО ВО (т.к. ВО (АВС))
Р
Рассмотрим ВОS:
N
у
А
х
В
=
SВ = 4, ВО =
S
С
О
О
900,
ВО =
4
О
4 3
3
В
4 3
3
По теореме Пифагора SО =
Координаты точки S:
S(
4
16
3
2
2 3
2
; 2; 4 )
3
3
16
16
1
2
4 1 4
3
3
3
2
3
ВN,
8.
Задача 511106z
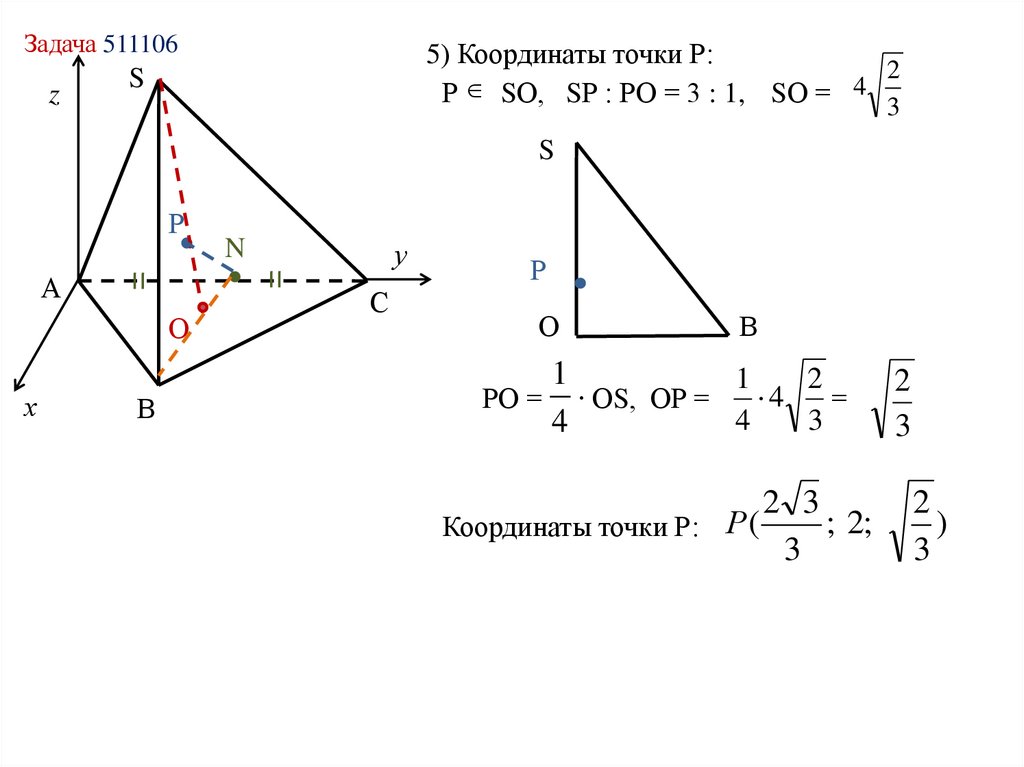
5) Координаты точки Р:
2
4
Р SО, SР : РО = 3 : 1, SО =
3
S
S
Р
А
О
х
В
N
у
С
Р
О
В
1
1
2
4
РО = ∙ ОS, ОР =
=
4
3
4
Координаты точки Р: Р(
2 3
; 2;
3
2
3
2
)
3
9.
Задача 511106Координаты точек: А(0;0;0), В ( 2 3;2;0), С(0;4;0), N(0;2;0), О (
S(
2 3
2 3
2
; 2;
; 2; 4 ), Р(
3
3
3
2
)
3
2 3
;2;0)
3
10.
Задача 511106z
а) Докажем, что NP BS
S
Рассмотрим векторы NP и BS. Если прямые
NP BS, то и векторы NP и BS перпендикулярны.
Р
А
О
х
у
N
С
Для доказательства перпендикулярности
векторов, найдём их скалярное произведение.
В
1) Найдём координаты вектора NР
2 3
2
2
;2;
); NР
0; 2 2;
N(0;2;0), Р(
3
3
3
2
2
2
0 ; NР ;0;
3
3
3
11.
Задача 511106z
S
В ( 2 3;2;0), S (
Р
А
О
х
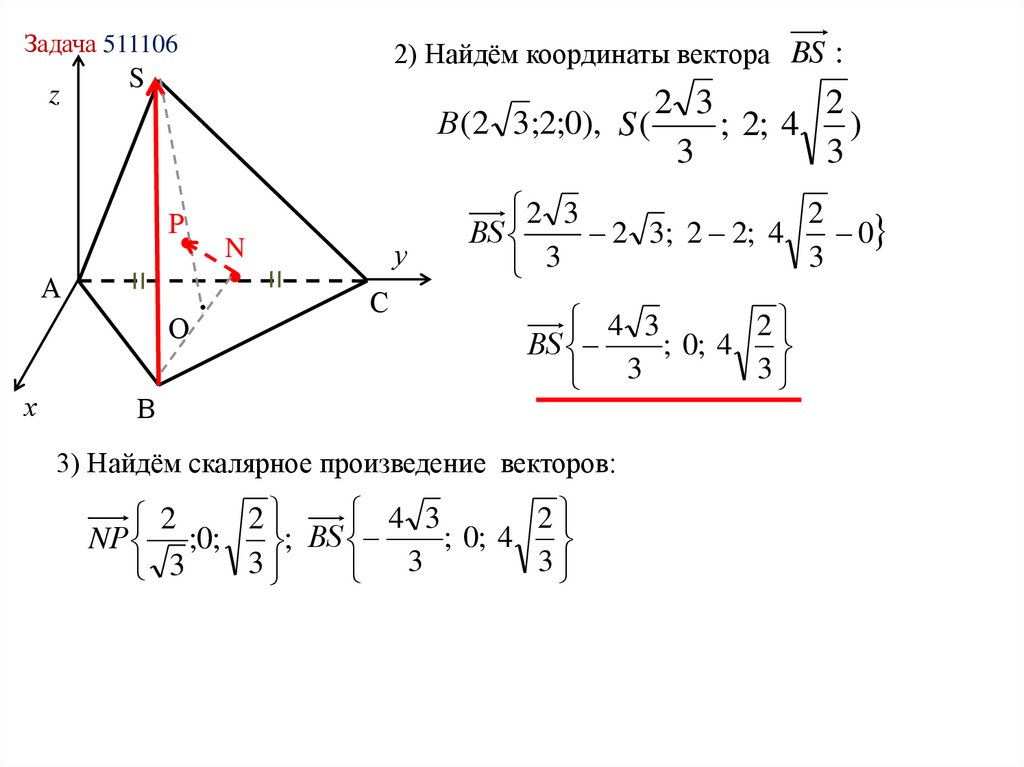
2) Найдём координаты вектора BS :
В
N
у
С
2 3
2
; 2; 4 )
3
3
2 3
2
ВS
2 3; 2 2; 4
0
3
3
4 3
2
ВS
; 0; 4
3
3
3) Найдём скалярное произведение векторов:
4 3
2
2
2
; 0; 4
NР ;0;
; ВS
3
3
3
3
12.
Задача 511106z
S
4 3
2
2
2
; 0; 4
NР ;0;
; ВS
3
3
3
3
Р
А
О
х
3) Найдём скалярное произведение векторов:
N
у
С
2
4
2
2
NР ВS
(
) 0 0
4
3
3
3
3
8 8
0
3 3
В
NР ВS 0, значит NР ВS , т.е. NР ВS
13.
Задача 511106z
б) Найдём расстояние от точки В до прямой NР
S
Проведём перпендикуляр из точки В к прямой РN:
ВН РN
Р
Н
В
у
N
А
С
О
N
х
Н
В
Рассмотрим
Р
NВН. Обозначим ВNН
ВН
sin
, тогда
ВN
ВН ВN sin
В
Если угол NВН – тупой, то ВН ВN sin( 180 )
Р
Н
N
14.
Задача 511106z
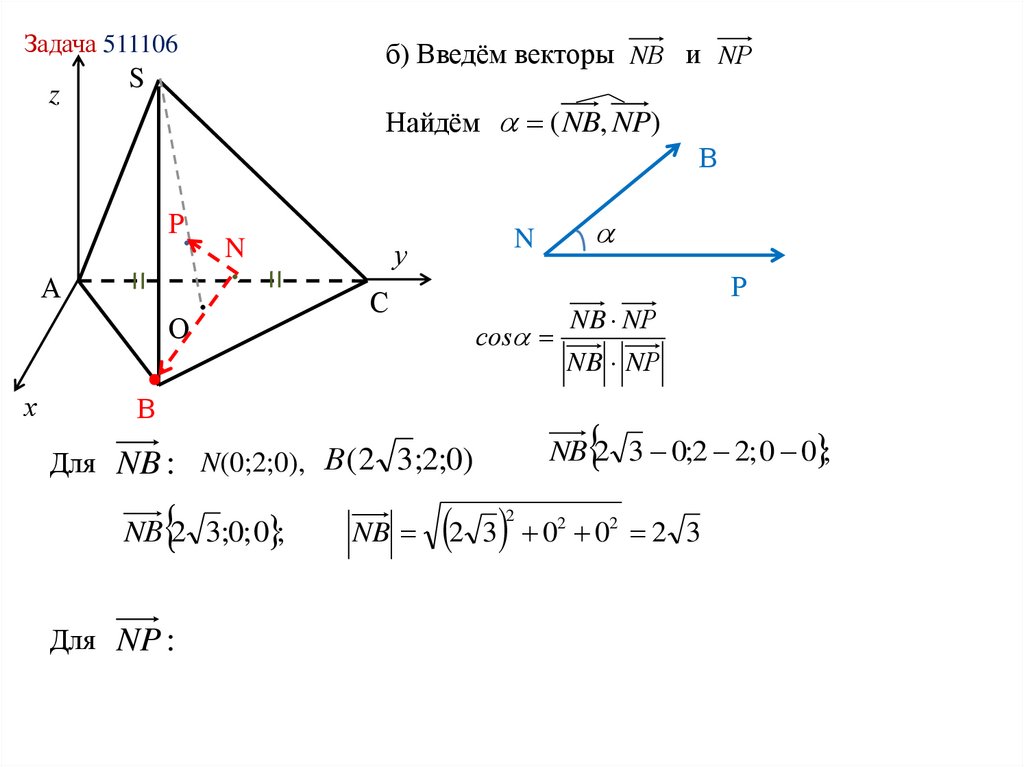
б) Введём векторы NВ и NР
S
Найдём ( NB, NP)
В
Р
N
А
О
х
у
С
Для NP :
NB
Р
NB NР
NВ 2 3 0;2 2; 0 0 ;
Для NB : N(0;2;0), В ( 2 3;2;0)
NB NР
соs
В
NВ 2 3;0; 0 ;
N
2 3 0
2
2
02 2 3
15.
Задача 511106z
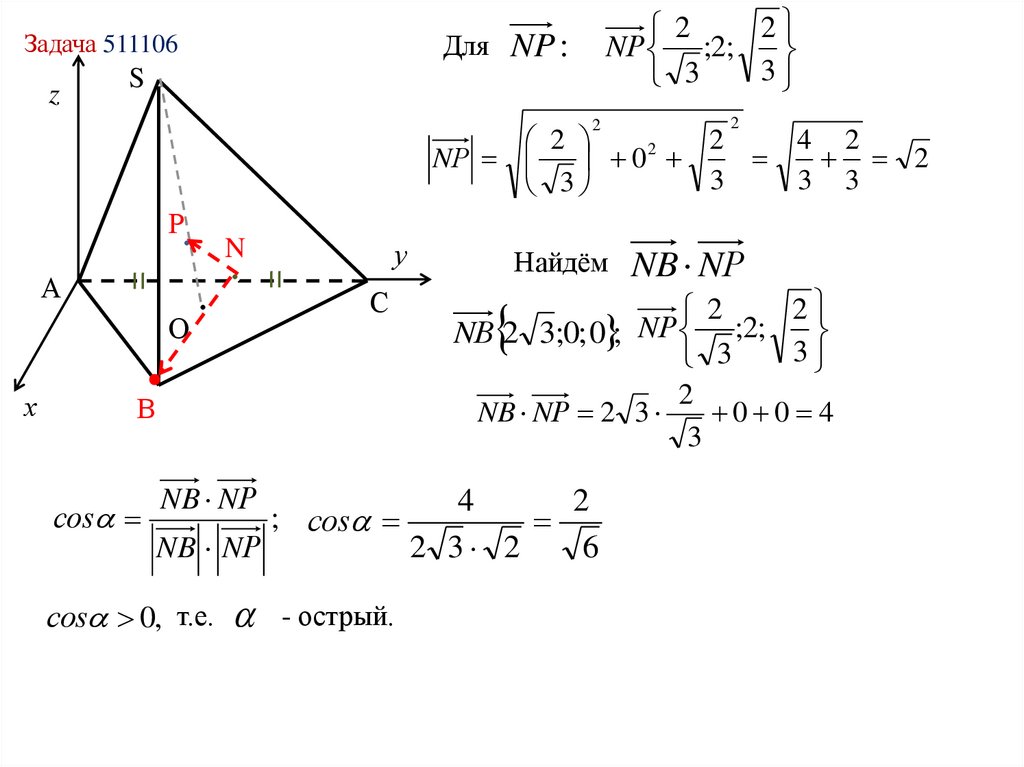
2
2
NР ;2;
3
3
Для NP :
S
2
2
2
2
2
NР
0
3
3
Р
N
А
С
О
х
у
В
соs
NB NР
NB NР
соs 0, т.е.
; соs
- острый.
Найдём
4 2
2
3 3
NB NР
2
2
NВ 2 3;0; 0 ; NР ;2;
3
3
2
NB NР 2 3
0 0 4
3
4
2
2 3 2
6
16.
ВЗадача 511106
z
S
Р
А
х
N
Н
у
N
С
В
Р
Н
ВН ВN sin
соs
2
6
Найдём sin из основного тригонометрического тождества:
2
4
1
2
2
sin 1
1
6
3
6
1
2
Вычислим ВН: ВН 2 3
3
Ответ: расстояние от точки В до прямой NР равно 2.
17.
Расстояние от точки до плоскостиПусть плоскость задана уравнением: ах + bу + сz + d = 0.
Дана точка М(х0,у0,z0). Расстояние от точки М до плоскости можно
вычислить по формуле:
l
ах0 bу 0 сz 0 d
a2 b2 c2
18.
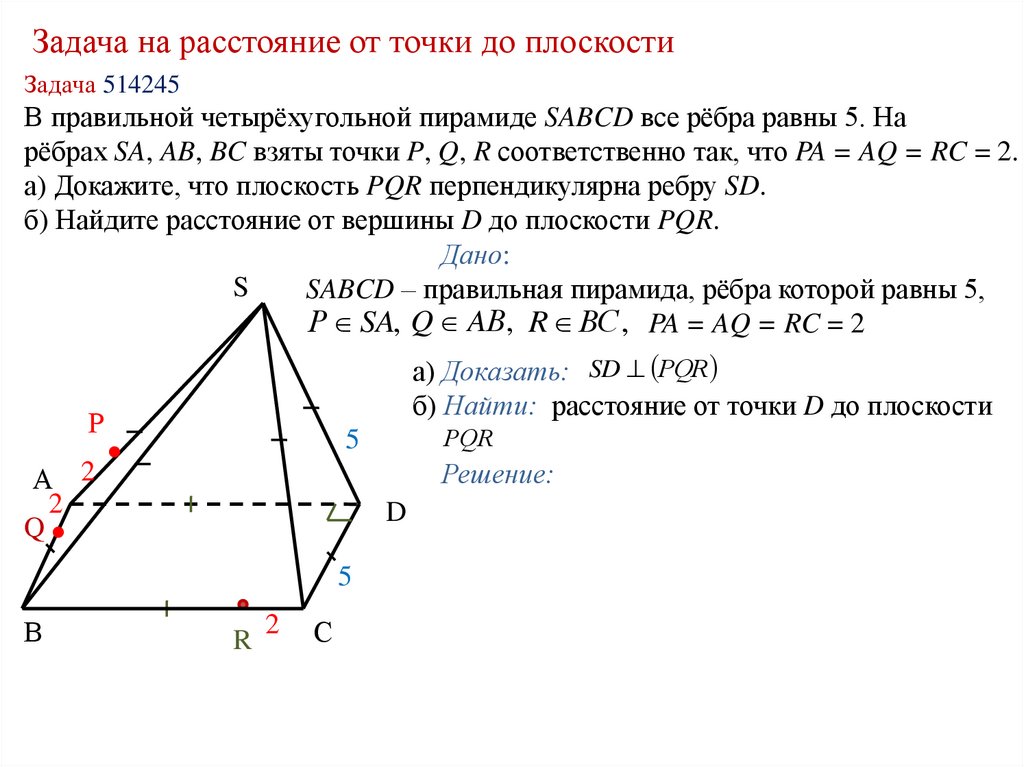
Задача на расстояние от точки до плоскостиЗадача 514245
В правильной четырёхугольной пирамиде SABCD все рёбра равны 5. На
рёбрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA = AQ = RC = 2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Дано:
S
SABCD – правильная пирамида, рёбра которой равны 5,
Р SA, Q AВ, R ВС , PA = AQ = RC = 2
а) Доказать: SD РQR
б) Найти: расстояние от точки D до плоскости
Р
Решение:
А 2
2
Q
D
5
В
РQR
5
R
2
С
19.
Задача 514245S
1) Введём прямоугольную систему координат.
Найдём координаты точек А, В, С, D, S, Р, Q и R.
А
2
Q
х
5
В
2) Координаты точек:
Р
2
А(0;0;0), В(5;0;0), (т.к. АВ = 5), D(0;5;0),
5 у (т.к. АD = 5), C(5;5;0).
D АQ = 2, тогда Q(2;0;0), RС = 2, RС = 2, то ВR= 3,
R(5;3;0)
R
2
С
20.
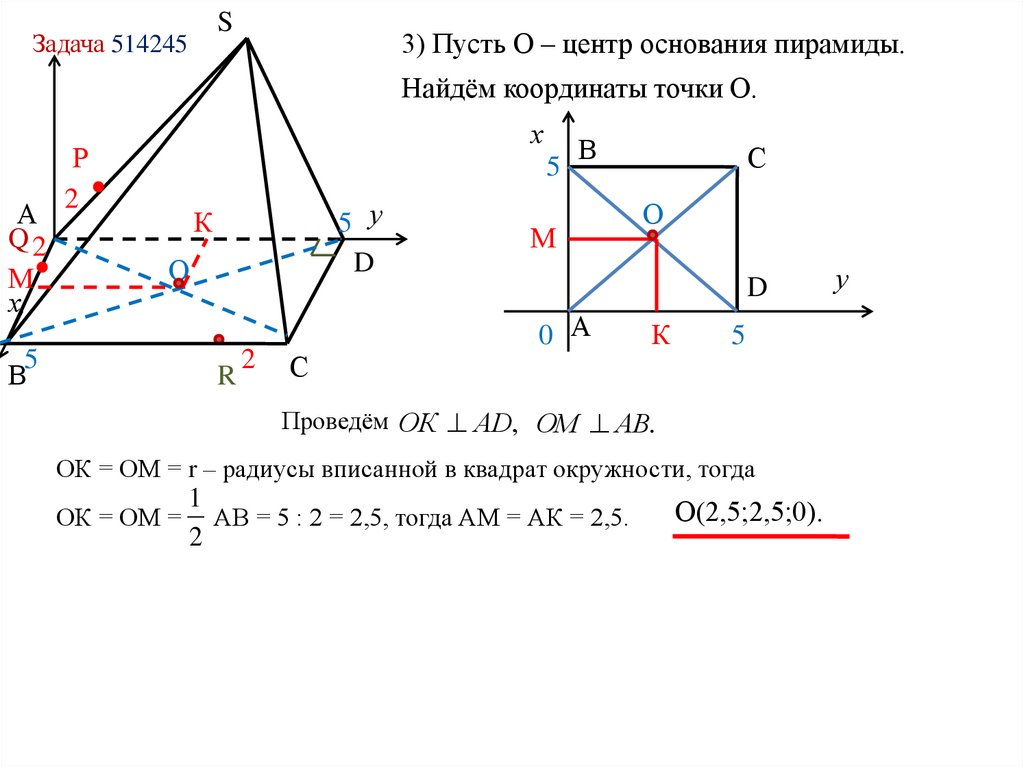
SЗадача 514245
3) Пусть О – центр основания пирамиды.
Найдём координаты точки О.
А
Q2
М
х
х
Р
2
5
5 у
D
К
О
5
В
R
2
В
М
С
О
D
0 А
К
5
С
Проведём ОК АD, ОМ АВ.
ОК = ОМ = r – радиусы вписанной в квадрат окружности, тогда
ОК = ОМ =
1
АВ = 5 : 2 = 2,5, тогда АМ = АК = 2,5.
2
О(2,5;2,5;0).
у
21.
Задача 514245S
4) Найдём координаты точки S.
Отрезок SО – высота правильной пирамиды,
z
А
х
5
В
тогда SО ( АВС ), т.е. SО перпендикулярна всем
прямым, лежащим в этой плоскости, SО АО.
Р
2
5 у
D
S(2,5;2,5;z), причём z = SО
Найдём SО из прямоугольного треугольника АSО.
О
R
С
2
2
В прямоугольном треугольнике АВС гипотенуза, АС 5 5 50 5 2
1
тогда АО = АС = 2,5 2
2
В прямоугольном треугольнике АSО катет SО найдём по теореме Пифагора:
5
25
5
SО АS 2 АО2 , SО 52 (2,5 2 )2 25 ( )2
2
2
2
5 5 5
)
Координаты точки S ( ; ;
2 2 2
22.
Задача 514245S
5) Найдём координаты точки Р.
Проведём РН ( АВС ), тогда РН АО, Н АО
z
А
Р
2
Н
х
5
В
Пусть Р(х;у;z), причём z = РН. Найдём РН
S
5 у
D
Р
5
2
О
R
С
А
Н
О
В прямоугольные треугольники АSО и АРН подобны по двум углам, тогда
АН РН АР 2
2
2 5
, т.е. РН SО
2, z 2
АО SО АS 5
5
5 2
2
2 5
2
Причём, АН АО
5
5 2
Найдём абсциссу и ординату точки Р.
23.
Задача 514245S
Найдём абсциссу и ординату точки Р, проведём
НЕ АВ, тогда, х = АЕ, у = ЕН
z
А
Е
х
Р
2
Н
5
В
5 у
D
О
А
Е
С
2
S
О
Н
О
М
5
R
5
2
С
В
Прямоугольные треугольники АМО и АЕН подобны по двум углам, тогда
АН ЕН
АЕ
5
, АН 2 , АО
, т.е. АН 2 : 5 2 ,
АО МО АМ
2
АО
5
2
2 5
тогда ЕН АЕ АМ 1,
5
5 2
Итак,
Р (1;1; 2 )
2
24.
Задача 514245S
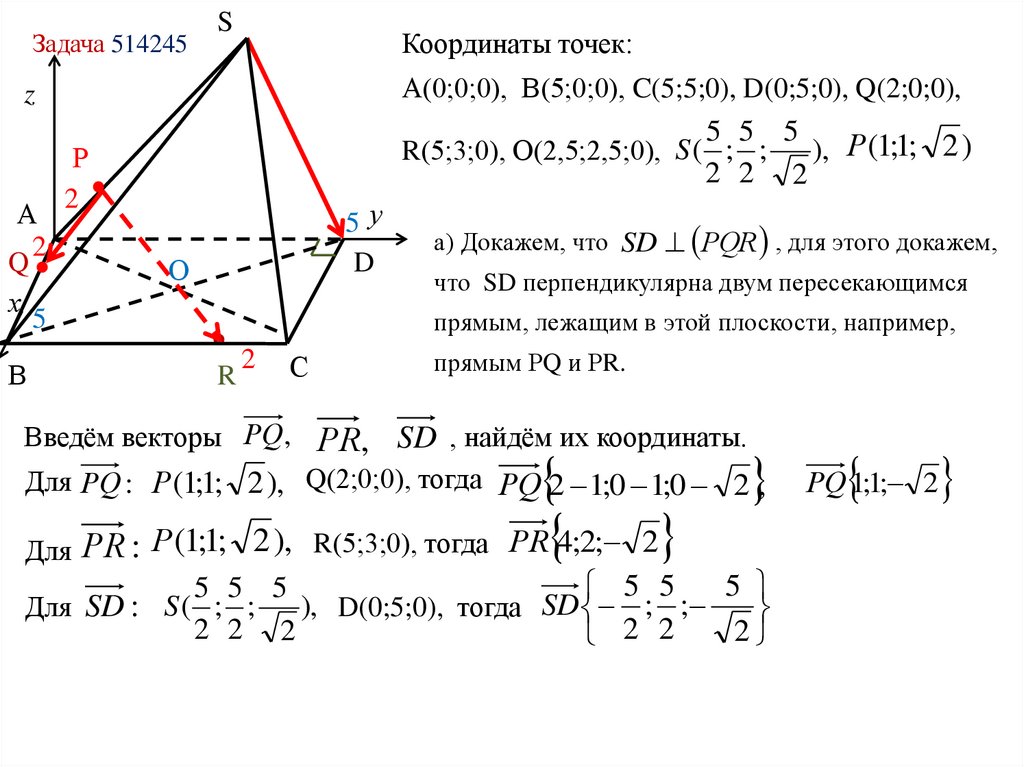
Координаты точек:
А(0;0;0), В(5;0;0), C(5;5;0), D(0;5;0), Q(2;0;0),
z
А
2
Q
х
5
5 5 5
), Р (1;1; 2 )
R(5;3;0), О(2,5;2,5;0), S ( ; ;
2 2 2
Р
2
В
5у
D
О
а) Докажем, что SD РQR , для этого докажем,
что SD перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости, например,
R
2
С
Введём векторы РQ,
прямым РQ и РR.
РR, SD , найдём их координаты.
РR 4;2; 2
Для РQ : Р (1;1; 2 ), Q(2;0;0), тогда РQ 2 1;0 1;0 2 ,
Для
РR : Р(1;1; 2 ), R(5;3;0), тогда
5
5 5
5 5 5
SD
;
;
), D(0;5;0), тогда
Для SD : S ( ; ;
2 2 2
2
2 2
РQ 1;1; 2
25.
Задача 514245S
Найдём скалярное произведение векторов
Р
А
у
Q
х
D
В
5
5 5
SD
;
;
РQ 1;1; 2 и
2
2 2
5
5
5
PQ SD 1 1 2
2
2
2
5 5
5 0, PQ SD 0, тогда
2 2
PQ SD, тогда прямые РQ SD
z
R
С
Найдём скалярное произведение векторов
РR 4;2; 2
5 5
5
и SD
; ;
2 2
2
5
5
5
PR SD 4 2 2
10 5 5 0
2
2
2
PR SD 0, тогда PR SD, тогда прямые SD РR.
Итак, прямая SD перпендикулярна двум пересекающимся прямым плоскости
РQR, а значит, SD (РQR ).
26.
Задача 514245S
Найдём расстояние от точки D до плоскости РQR.
z
Расстояние от точки D(х0,у0,z0) до плоскости
Р
А
у
Q
х
D
В
R
2
С
, заданной уравнением ах + bу + сz + d = 0
можно вычислить по формуле:
l
ах0 bу 0 сz 0 d
a2 b2 c2
Причём, D(0;5;0).
Запишем уравнение плоскости, проходящей через точки Q(2;0;0), R(5;3;0),
Р (1;1; 2 )
В уравнение плоскости подставим координаты точек.
27.
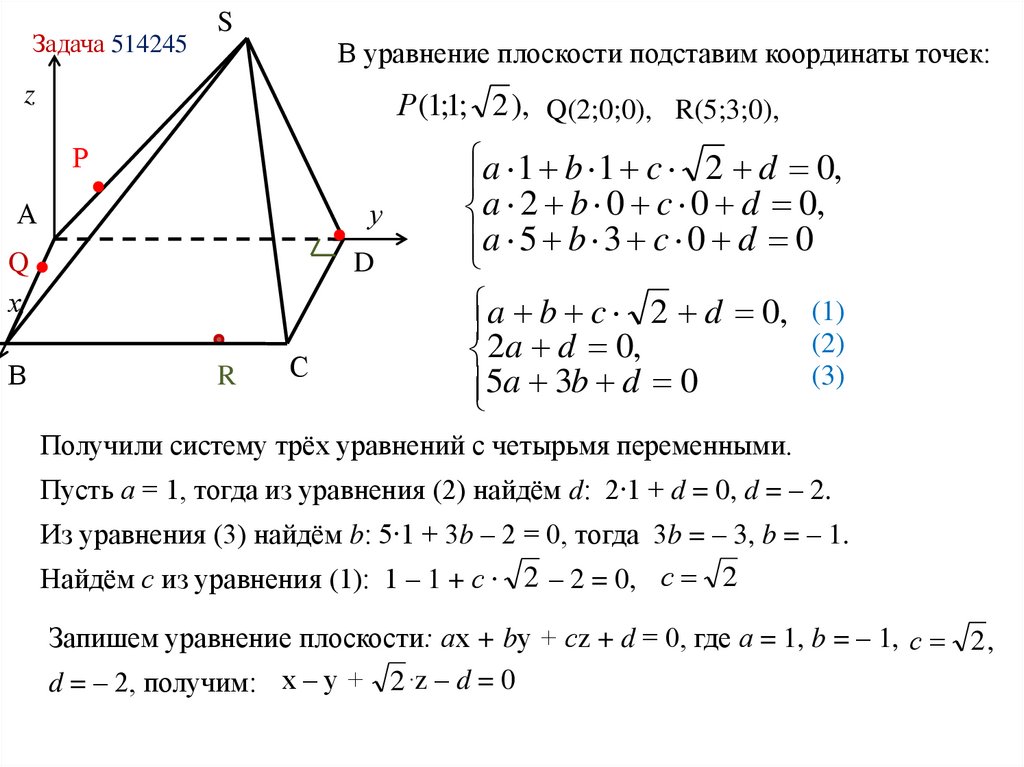
Задача 514245S
В уравнение плоскости подставим координаты точек:
z
Р (1;1; 2 ), Q(2;0;0), R(5;3;0),
Р
А
у
Q
х
D
В
R
С
a 1 b 1 c 2 d 0,
a 2 b 0 c 0 d 0,
a 5 b 3 c 0 d 0
a b c 2 d 0, (1)
(2)
2a d 0,
(3)
5a 3b d 0
Получили систему трёх уравнений с четырьмя переменными.
Пусть а = 1, тогда из уравнения (2) найдём d: 2∙1 + d = 0, d = – 2.
Из уравнения (3) найдём b: 5∙1 + 3b – 2 = 0, тогда 3b = – 3, b = – 1.
Найдём с из уравнения (1): 1 – 1 + с 2 – 2 = 0, с 2
Запишем уравнение плоскости: ах + bу + сz + d = 0, где а = 1, b = – 1, с 2 ,
d = – 2, получим: х – у + 2 ∙z – d = 0
28.
Задача 514245S
Найдём расстояние от точки D(0;5;0) до плоскости
РQR, заданной уравнением х – у + 2 ∙z – d = 0
z
Р
А
у
Q
х
D
В
l
ах0 bу 0 сz 0 d
a2 b2 c2
где х0 =0, у0 =5, z0 =0, а = 1, b = – 1, с 2 , d = – 2,
R
С
получим:
( D, ( РQR )) l
0 5 0 2
1 1 2
2
2
2
Ответ: расстояние от точки D до плоскости РQR равно 3,5
7
4
7
3,5
2
29.
Задача 514245S
Вернёмся к пункту а), докажем, что прямая SD
z
перпендикулярна плоскости РQR, зная уравнение
данной плоскости:
Р
А
у
Q
х
D
В
R
С
х – у + 2 ∙z – d = 0
Найдём угол между прямой SD и
плоскостью РQR, докажем что он равен 900
30.
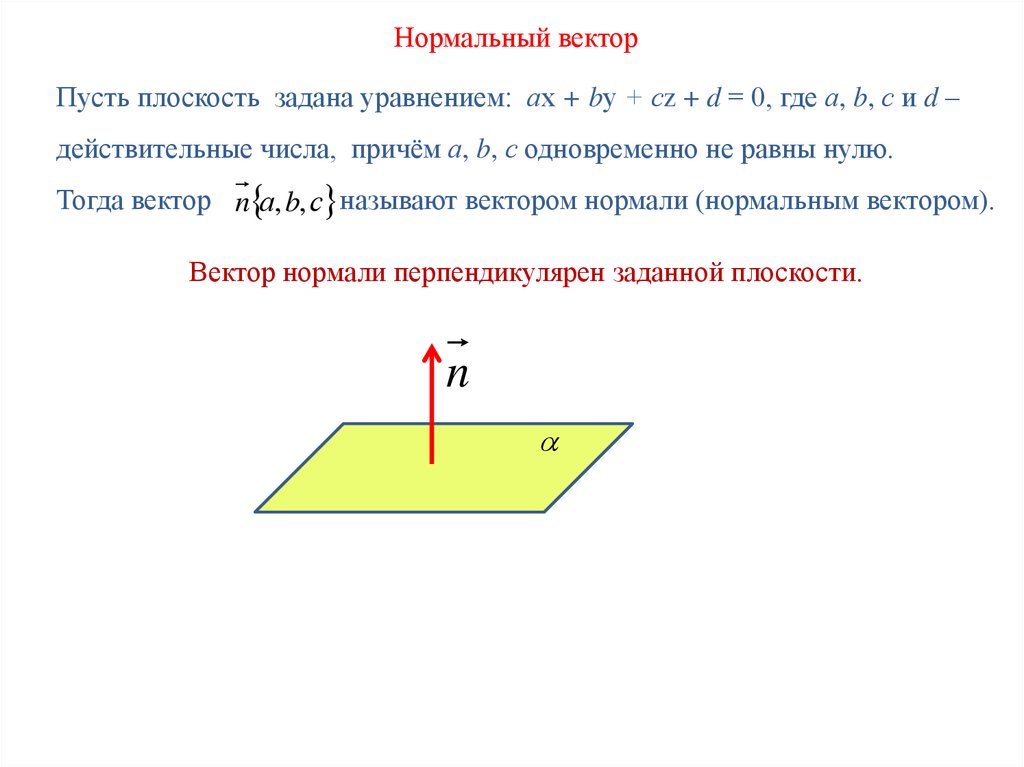
Нормальный векторПусть плоскость задана уравнением: ах + bу + сz + d = 0, где а, b, с и d –
действительные числа, причём а, b, с одновременно не равны нулю.
Тогда вектор n а, b, с называют вектором нормали (нормальным вектором).
Вектор нормали перпендикулярен заданной плоскости.
n
31.
Угол между прямой, пересекающей плоскость, и этой плоскостьюПусть плоскость задана уравнением: ах + bу + сz + d = 0,
n а, b, с -
вектор нормали к этой плоскости, прямая АВ пересекает плоскость.
Пусть
- угол между прямой АВ и плоскостью, тогда угол между
прямой АВ и вектором
n
= 900 А
n
В
32.
Задача 514245S
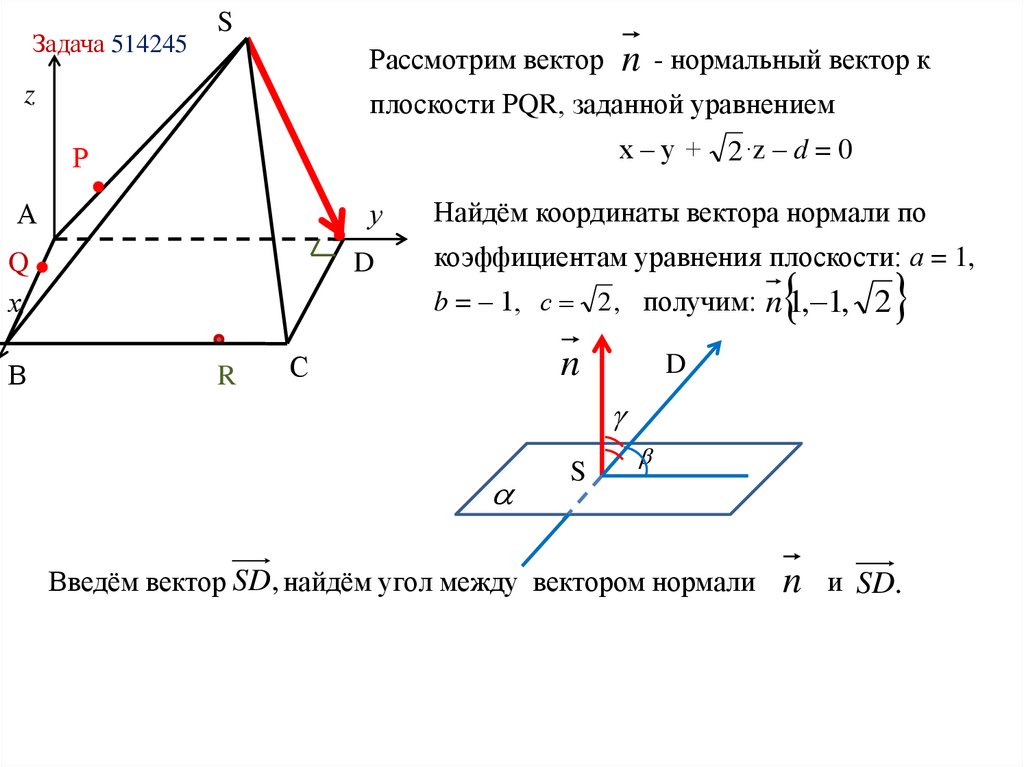
Рассмотрим вектор
z
- нормальный вектор к
плоскости РQR, заданной уравнением
х – у + 2 ∙z – d = 0
Р
А
у
Q
х
D
В
n
Найдём координаты вектора нормали по
коэффициентам уравнения плоскости: а = 1,
n
и SD.
b = – 1, с 2 , получим: n 1, 1, 2
R
n
С
D
S
Введём вектор SD, найдём угол между вектором нормали
33.
Задача 514245S
n
z
D
Р
А
у
Q
х
D
S
Найдём угол между векторами
В
С
R
соs
SD n
SD n
,
5
5 5
SD ; ;
, n 1, 1, 2
2
2 2
5 5
5
10
2 2
соs
1
25 25 25 2 2 25
1 1 2
4
4
4
Получаем, что векторы противоположно направлены, значит они лежат на
параллельных прямых. n - вектор нормали к плоскости PQR, тогда n PQR
значит SD PQR , тогда SD PQR.
34.
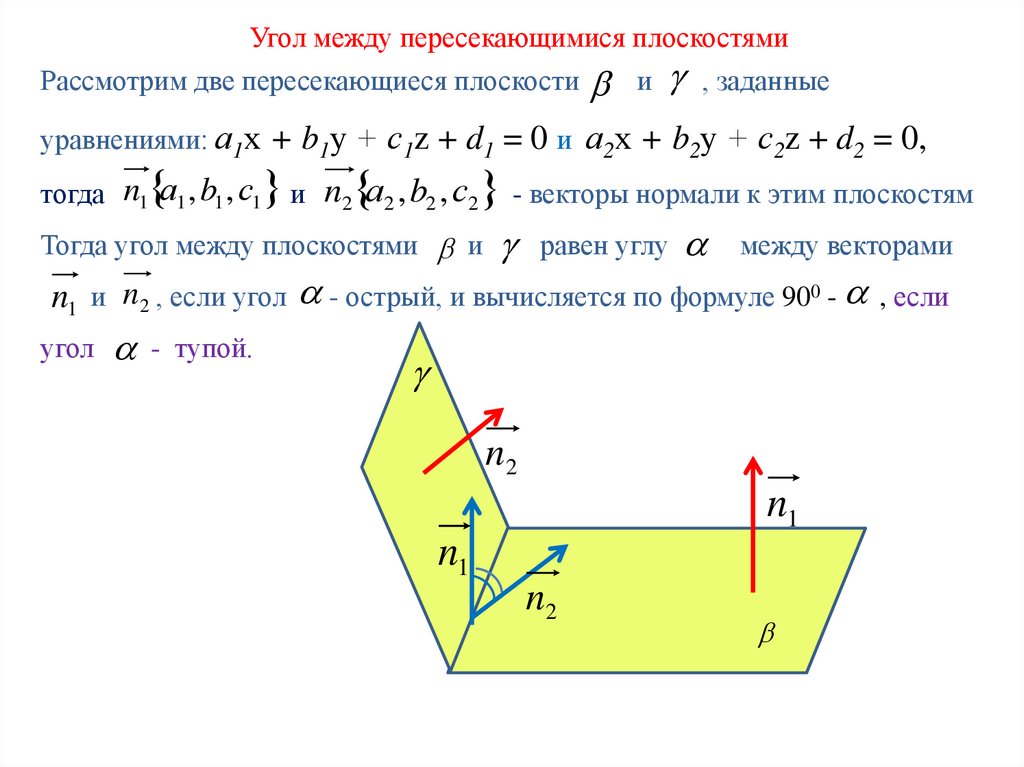
Угол между пересекающимися плоскостямиРассмотрим две пересекающиеся плоскости
и
, заданные
уравнениями: а1х + b1у + с1z + d1 = 0 и а2х + b2у + с2z + d2 = 0,
тогда n1 а1 , b1 , с1 и n2 а2 , b2 , с2 - векторы нормали к этим плоскостям
Тогда угол между плоскостями и
равен углу
между векторами
n1 и n2 , если угол - острый, и вычисляется по формуле 900 - , если
угол
- тупой.
n2
n1
n1
n2
35.
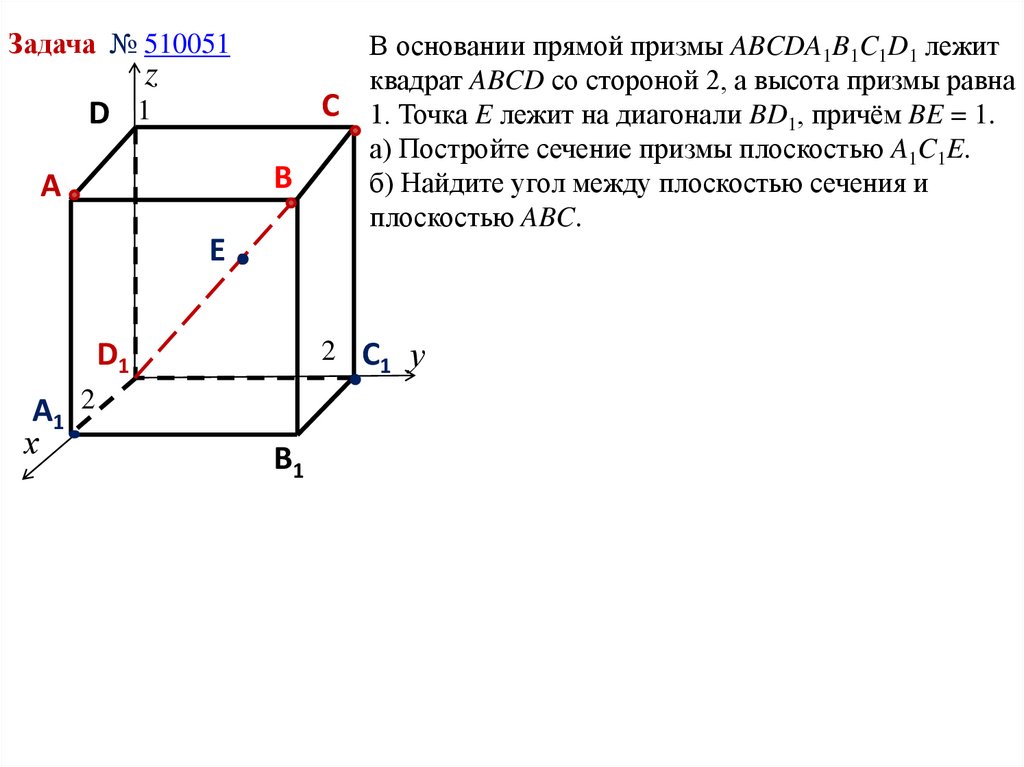
Задание № 510051В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной
2, а высота призмы равна 1. Точка E лежит на диагонали BD1, причём BE = 1.
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
36.
Задача № 510051z
C
D 1
B
A
В основании прямой призмы ABCDA1B1C1D1 лежит
квадрат ABCD со стороной 2, а высота призмы равна
1. Точка E лежит на диагонали BD1, причём BE = 1.
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и
плоскостью ABC.
Е
2 C1 у
D1
A1 2
х
B1
37.
Задача на расстояние между скрещивающимися прямымиЗадача 519659
В правильной треугольной призме АВСА1В1С1 все рёбра равны 2.
Точка M — середина ребра АА1 .
а) Докажите, что прямые MB и ВС1 перпендикулярны.
б) Найдите расстояние между прямыми MB и В1С.
А1
С1
В1
М
2
А
С
2
В
Дано:
АВСА1В1С1 – правильная пирамида, рёбра которой
равны 2, M — середина АА1
а) Доказать: MB ВС1 .
б) Найти: расстояние между прямыми MB и В1С.
Решение:
б) Найдем расстояние между прямыми MB и В1С.
38.
Задача 519659б) Найдем расстояние между прямыми MB и В1С.
А1
С1 Прямые MB и В С являются скрещивающимися.
1
В1
Расстоянием между скрещивающимися прямыми
М
2
А
С
Х
В 2
является расстояние от одной из этих прямых до
плоскости, содержащей другую прямую, и
параллельную первой.
Построим плоскость, параллельную прямой В1С,
проходящую через прямую MB.
Проведём прямую МХ, параллельную прямой В1С. Тогда по признаку
параллельности прямой и плоскости прямая В1С параллельна плоскости MBХ.
Найдем расстояние от прямой В1С до плоскости MBХ, для этого на прямой В1С
выберем точку, например, точку С, найдём расстояние от точки С до плоскости
MBХ по формуле:
r
ах0 bу0 сz 0 d
a 2 b2 c 2
39.
Задача 519659А1
2
z
б) Введём прямоугольную систему координат.
С1
Нам необходимо задать уравнение плоскость МВХ и
В1
найти координаты точки С.
Найдём координаты точек: С(0;2;0), М(0;0;1).
М
х
2у
Н
А
Пусть Х - точка пересечения прямой МХ и плоскости
Х
АВС, тогда Х(х;у;0).
С
Найдём х и у. Рассмотрим векторы В1С и МХ
Найдём их координаты.
В
Найдём координаты точки В. Треугольник АВС – равносторонний, со стороной 2.
х
Проведём ВН – высоту треугольника, АН = 1, тогда по
В
теореме Пифагора ВН 22 12 3.
координаты точки В: В ( 3;1;0)
2
Тогда координаты точки В1: В1 ( 3;1;2)
А
С
Н
0
1
2
у
40.
Задача 519659А1
2
х
z
С1
В1
Х(х;у;0)
Найдём х и у. Рассмотрим векторы В1С и МХ
Векторы лежат на параллельных прямых, а значит
М
коллинаерны, тогда их координаты пропорциональны.
А
Найдём координаты векторов В1С и МХ
Для В1С : В1 ( 3;1;2), С(0;2;0), тогда В1С 3;1; 2
2у
Х
В
С
Для МХ : М(0;0;1), Х(х;у;0), тогда МХ х; у; 1
Учитывая коллинеарность векторов, получаем:
3 1 2
х
у 1
3 2
1 2
1
3
у
Из равенства у 1 находим
. Из равенства х
1 находим х 2
2
Получаем координаты точки Х: Х (
3 1
; ;0)
2 2
41.
Задача 519659А1
2
z
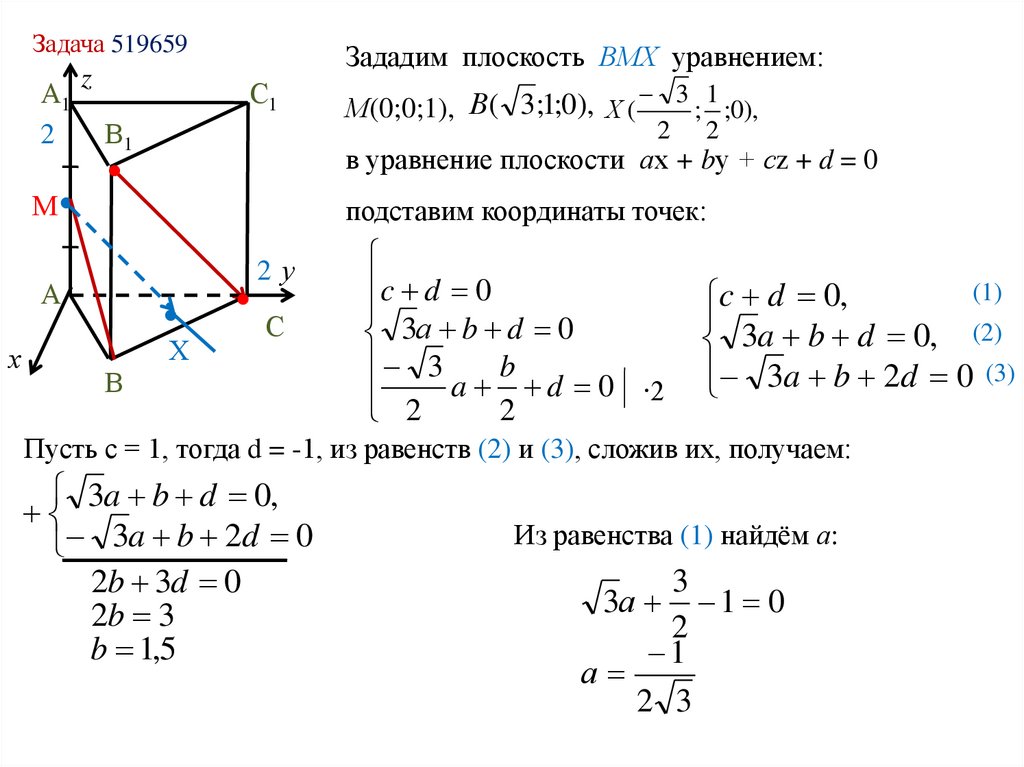
Зададим плоскость ВМХ уравнением:
С1
В1
2
2
в уравнение плоскости ах + bу + сz + d = 0
М
подставим координаты точек:
2у
А
х
3 1
М(0;0;1), В ( 3;1;0), Х (
; ;0),
Х
С
В
c d 0
3а b d 0
3
b
a
d 0 ∙2
2
2
(1)
c d 0,
3a b d 0, (2)
3a b 2d 0 (3)
Пусть с = 1, тогда d = -1, из равенств (2) и (3), сложив их, получаем:
3a b d 0,
3a b 2d 0
2b 3d 0
2b 3
b 1,5
Из равенства (1) найдём а:
3
3а 1 0
2
1
а
2 3
42.
Задача 519659А1
2
Уравнение плоскости ВМХ :
z
С1
В1
1
3
, b , с 1, d 1
2
2 3
2 3
3
у z 1 0
2
Координаты точки С: С(0;2;0).
М
2у
А
х
где а
х
Найдём расстояние от точки С до плоскости ВМХ
С
Х
r
В
r
Ответ:
0 3 0 1
1 9
1
12 4
30
5
ах0 bу0 сz 0 d
a 2 b2 c 2
2
10
30
2:
3
5
28
1
12





























 Математика
Математика








