криволін.трапеція

1.

Знаходження площ криволінійних
трапецій

2.

Завдання 1. Побудуйте схематично фігури, площі
яких виражаються такими інтегралами:
1
xdx
0
2
2
x
dx
1
2
cos xdx
0
3
dx
1 x

3.

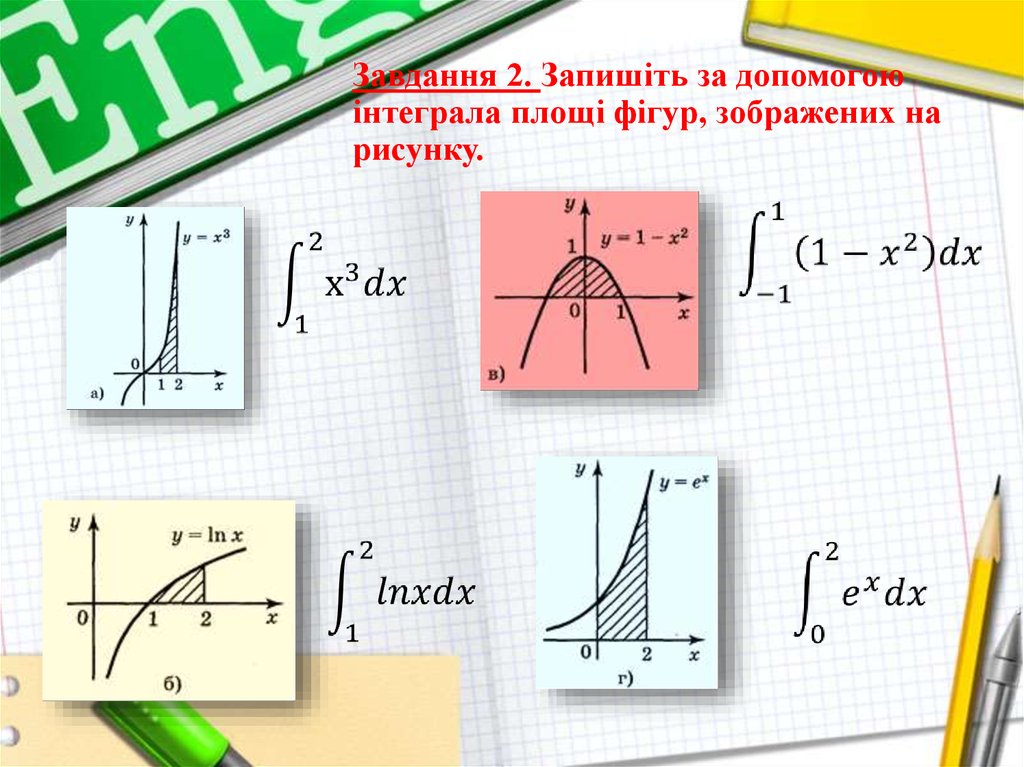
Завдання 2. Запишіть за допомогою
інтеграла площі фігур, зображених на
рисунку.

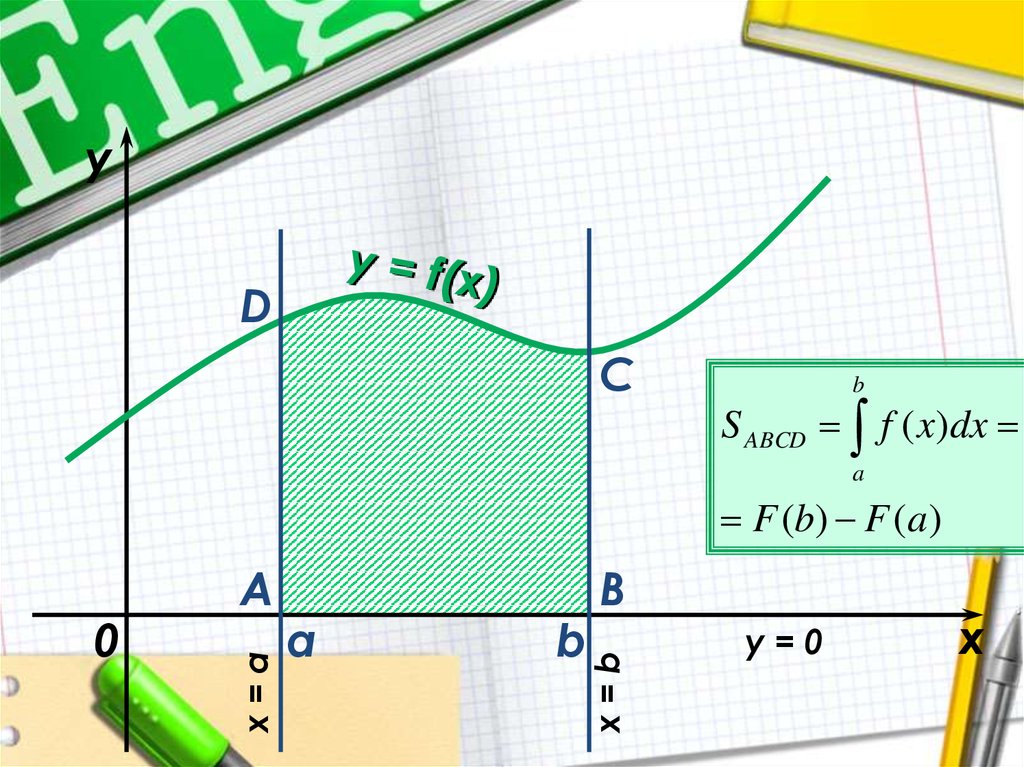
4. Теорема:

Якщо f-неперервна і невід’ємна на
[а, b] функція, а F-її первісна, то
площа S відповідної криволінійної
трапеції дорівнює приросту
первісної на відрізку [а, b], тобто
S=F(b)-F(a)

5. Знаходження площ криволінійних трапецій

6.

y
D
C
b
S ABCD f ( x)dx
a
F (b) F (a)
a
b
B
x=b
x=a
0
A
y=0
x

7.

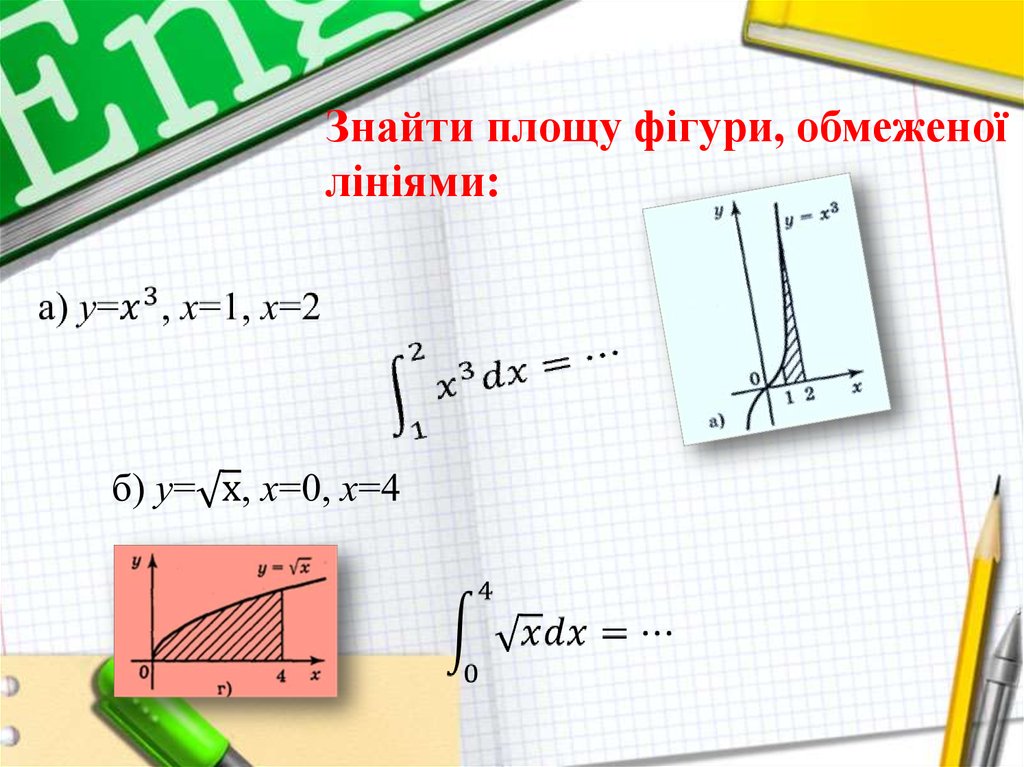
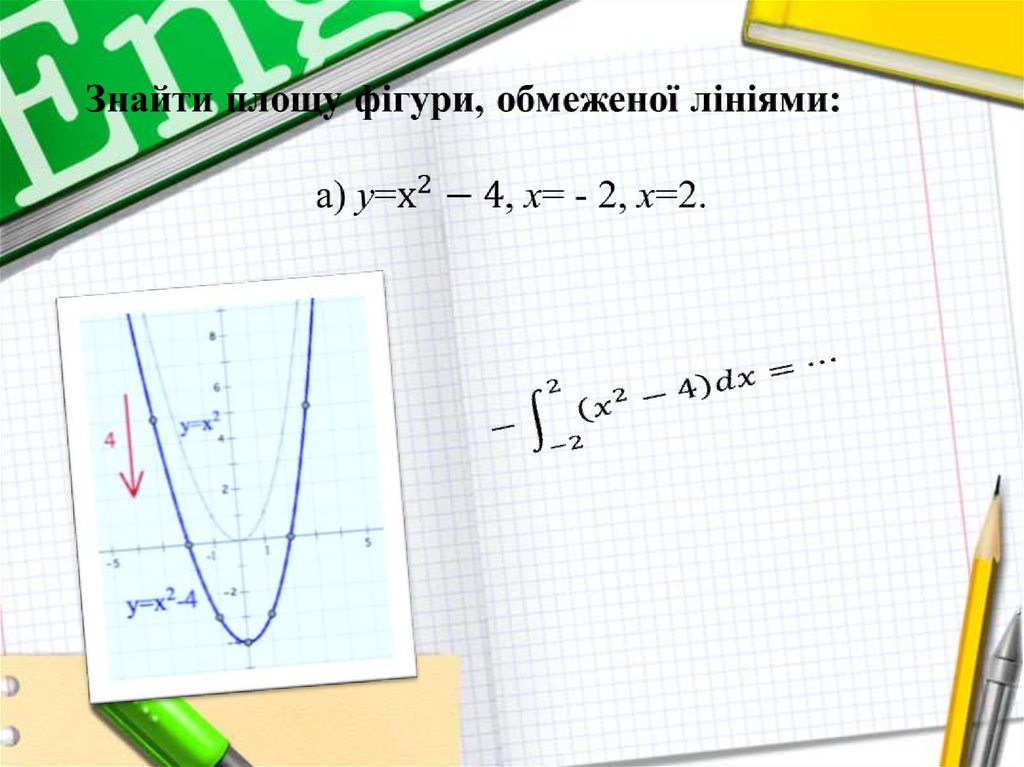
Знайти площу фігури, обмеженої
лініями:

8.

y
B
b
y=0
x
b
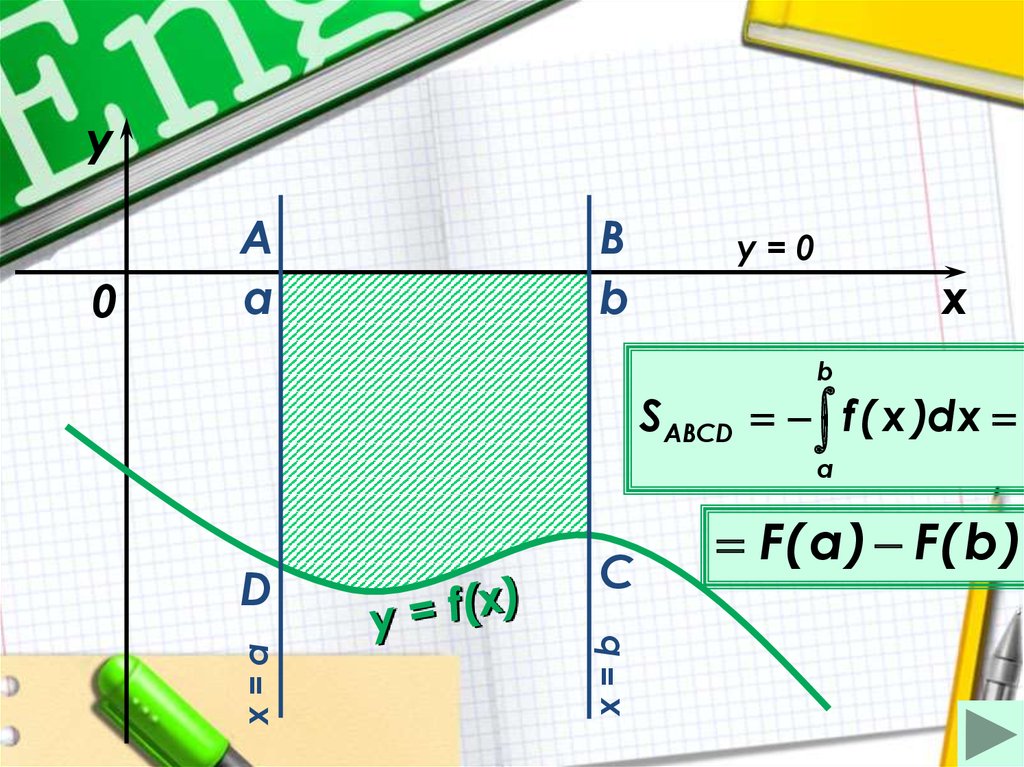
S ABCD f ( x )dx
D
C
x=b
a
x=a
0
A
a
F( a ) F( b )

9.

10.

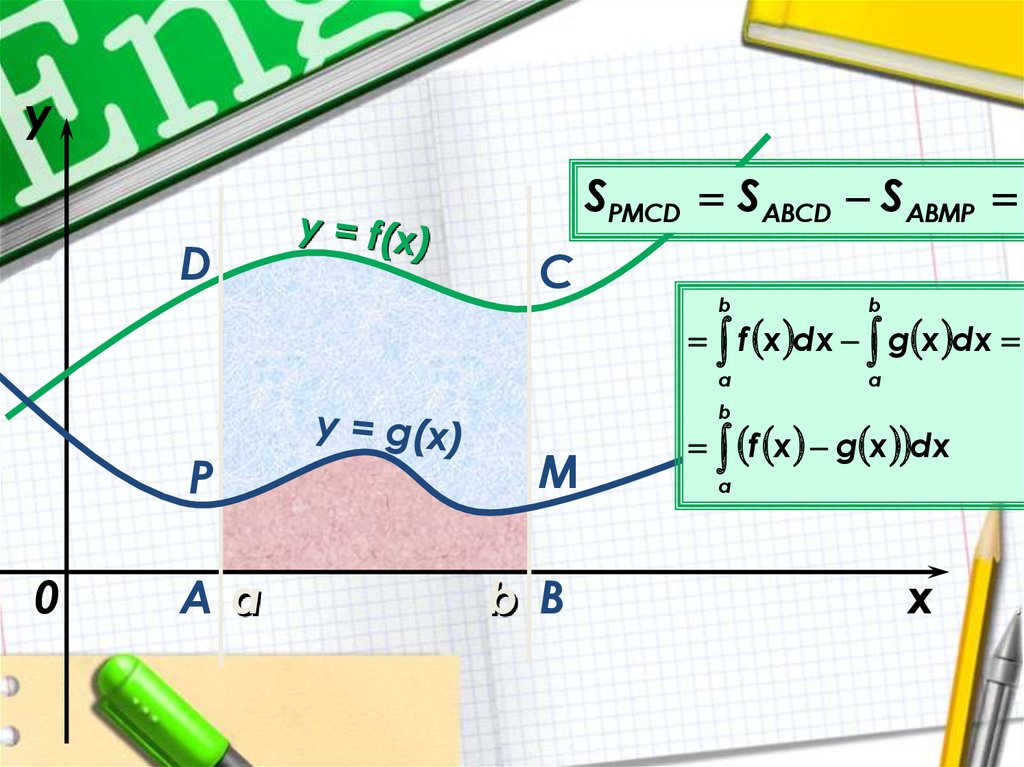
y
SPMCD SABCD SABMP
D
C
b
b
a
a
f x dx g x dx
b
P
0
Aa
M
b B
f x g x dx
a
x

11.

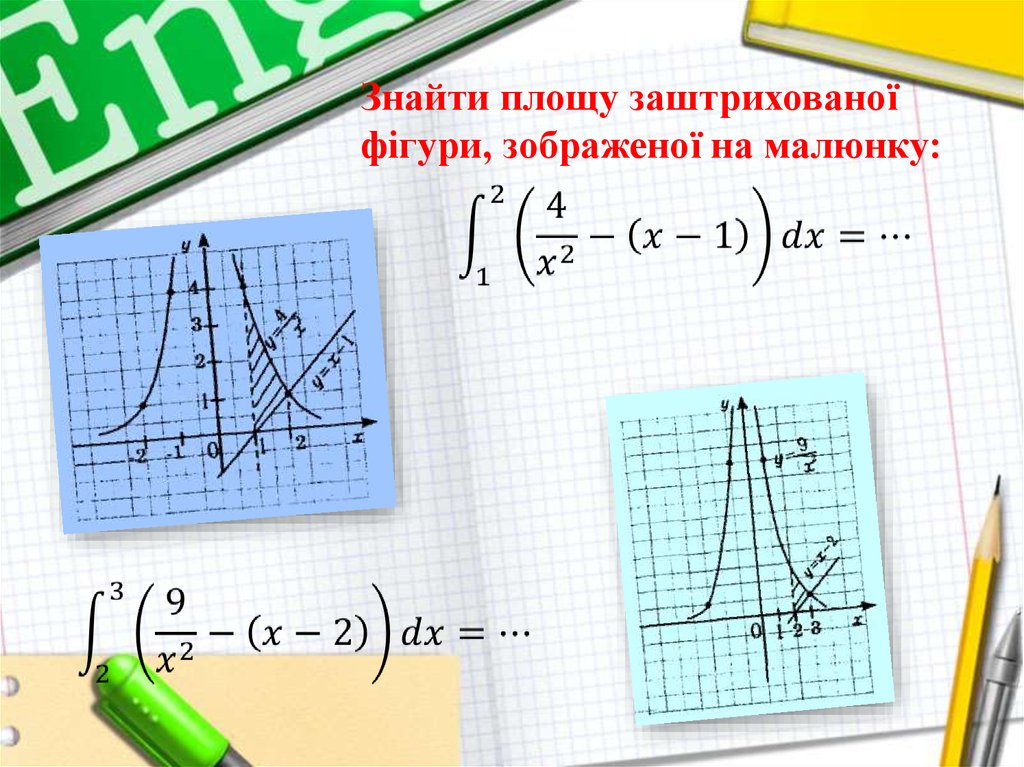
Знайти площу заштрихованої
фігури, зображеної на малюнку:

12.

y
SАЕDВ SAEDC SСDB
с
b
a
с
f x dx g x dx
D
Е
0
Aa
с
C
b
B
x