Понятие производной.Правила дифференцирования ._

1.

2.

В прямоугольной (декартовой) системе координат зададим
функцию y = f (x) и будем рассматривать Х и У как чисто математические
величины, не приписывая им никакого физического содержания. Пусть х произвольная точка, лежащая в некоторой окрестности точки Х0.
1. Дадим аргументу Х0 приращение ∆x (см.рис.1): тогда x = Х0 + ∆x.
2. И функция y получит приращение ∆ у и новое значение
у + ∆ у = f (x0 + ∆x).
3. Найдем приращение аргумента и приращение функции:
∆x = x - Х0
и ∆ у = f(x0+∆x) – f(x0).
4. Составим отношение приращения функции к приращению аргумента:
y f ( x0 x) f ( x0 ) (1)
x
x
5. Перейдем к пределу выражения (1):
f ( x0 x) f ( x0 )
y
lim
lim
(2)
x
x
Рис.1

3.

6. Если существует предел отношения (2) при ∆x стремящемся к нулю, то
f ( x0 x) f ( x0 )
y
lim
lim
при x 0
x
x
(3)
его называют производной данной функции y = f (x) и обозначают:
dy
y или f (x) или
. Таким образом,
dx
y
y lim
x
при x 0
ОПРЕДЕЛЕНИЕ
Производной данной функции y = f (x) при данном
значении аргумента х0 называется предел
отношения приращения функции ∆ у к
приращению аргумента ∆x, когда ∆x
произвольным образом стремится к нулю.

4.

Если такого предела не существует, то данная
функция в точке х0 производной не имеет. В том
случае, когда предел равен , говорят, что
существует бесконечная производная.
Если функция у = f (х) имеет конечную
производную в точке x0 , то говорят, что она
дифференцируема в точке x0.
Нахождение производной такой функции
называется дифференцированием.

5.

6.

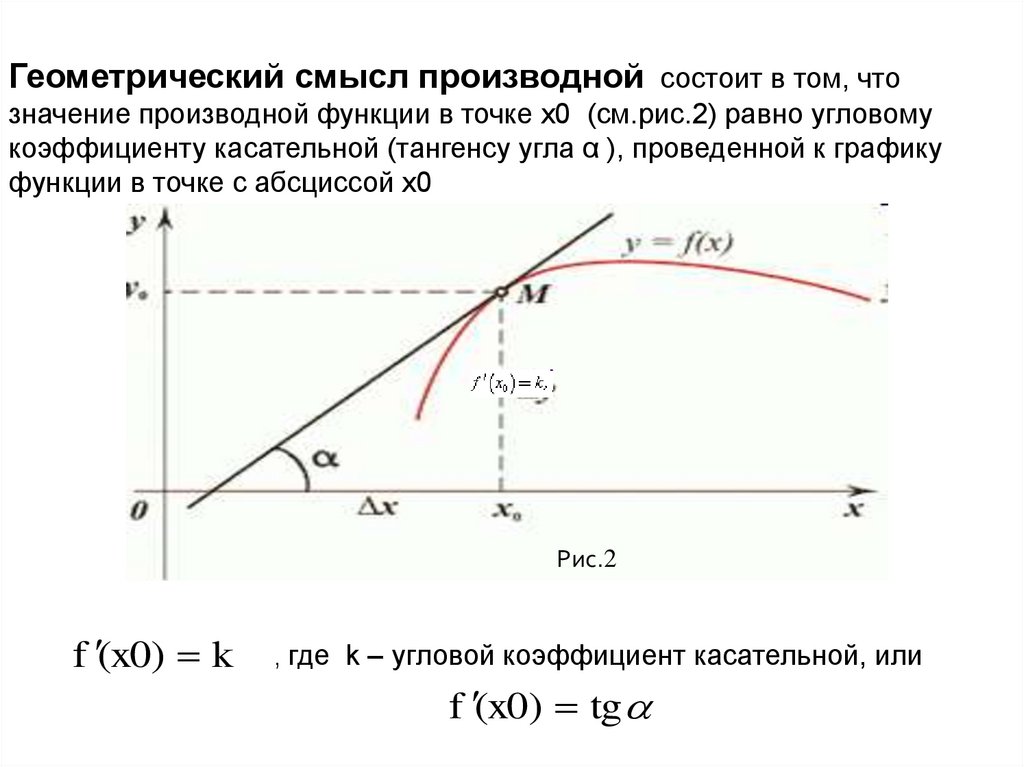
Геометрический смысл производной состоит в том, что
значение производной функции в точке x0 (см.рис.2) равно угловому
коэффициенту касательной (тангенсу угла α ), проведенной к графику
функции в точке с абсциссой x0
Рис.2
f (x0) k
, где k – угловой коэффициент касательной, или
f (x0) tg

7.

Пусть материальная точка движется по координатной прямой по закону x
= V(t) , т.е. координата этой точки х – известная функция времени t.
Физический смысл производной состоит в том, что производная
от координаты по времени есть мгновенная скорость:
V(t) x (t ) lim
x
t
при t 0
Примеры:
Движение автомобиля, поезда,человека и т.д.
Но можно говорить и о других смыслах: например,экономическом:
Скорость падения акций на рынке ценных бумаг, изменение курса валют,
падение покупательского спроса на определенные виды товаров,
изменение инфляции, зарплаты и т.д.

8.

9.

Правило 1
Если функции u и v дифференцируемы в точке x0,
то их сумма также дифференцируема в точке x0,
причем производная суммы равна сумме
производных, т.е.
( + )'= ' + '
Правило 2
Если функции u и v дифференцируемы в точке
x0, то их произведение также дифференцируемо в
точке x0, причем
( ∙ )' = ' + '

10.

Правило 3
Если функции и дифференцируемы в точке х0 и
(х0 ) ≠ 0, то их частное также дифференцируемо в точке
x0, причем
( / )' = ( ' - ') / ²
Правило 4
Если функция u дифференцируема в точке x0 и с =
const, то их произведение также дифференцируемо в
точке x0 , при чем (сu)' = сu'.
Правило №5
Если f (g(х)) - сложная функция, то ее производная
равна произведению производных внешней и внутренней
функций, т.е.
[f(g(x))]'= f '(g) ◦ g'(x)

11.

12.

Опираясь на математическое определение производной (3), а также на ее
физический и геометрический смысл, можно найти производные всех
основных элементарных функций.
Пример 1. Пусть y=f(x)=C (С – произвольная константа). Найдем
производную y′ этой функции. То есть найдем производную C′ константы С.
Решение
Способ 1 – геометрический.
Графиком функции y=C является горизонтальная прямая. Касательной к
этой прямой, проведенной в любой ее точке, будет она сама. Ее угол
наклона α к оси ох равен нулю. Но tg0=0. Значит, y′=C′=0.
Способ 2 – физический.
Функция y=C от x не зависит, то есть с изменением x не меняется. А
значит, скорость v(x) ее изменения равна нулю. Но ведь скорость
изменения функции – это производная функции. Таким образом, если
y=C, то y′=C′=0. Физический смысл этого вывода очевиден: если
координата y движущейся точки неизменна, то точка стоит. А значит,
скорость ее движения равна нулю.

13.

Опираясь на математическое определение производной (3), а также на ее
физический и геометрический смысл, можно найти производные всех
основных элементарных функций.
Пример 1. Пусть y=f(x)=C (С – произвольная константа). Найдем
производную y′ этой функции. То есть найдем производную C′ константы С.
Решение
Способ 3 – математический.
Воспользуемся математическим определением (3)
производной функции:
Вывод: если y = C, то y ′= C′ = 0.

14.

Пример 2. Пусть y=f(x)= х. Найдем производную y′ этой функции.
Решение
Способ 1 – геометрический.
Графиком функции y=х является прямая, представляющая
собой биссектрису первого и третьего координатных углов. Ее
угол наклона к оси ОХ составляет 45º. Касательная к этой
прямой в любой ее точке (при любом x) совпадает с этой же
прямой. Поэтому, опираясь на геометрический смысл
производной, получаем: y′=x′=tg45º=1. То есть
x′=1.Касательной к этой прямой, проведенной в любой ее
точке, будет она сама. Но tg45º=1. Значит, y′=х′=1.

15.

Решение
Способ 3 – математический.
Воспользуемся математическим определением (3)
производной функции:
Вывод: если y = х, то y ′= х′ = 1.

16.

Пример 3. Пусть y=f(x)=x2 . Найдем производную y′ этой функции.
Решение
Способ 3 – математический.
Воспользуемся математическим определением (3)
производной функции:
Итак, если y=x2, то y′ =(x2)′ =2x.