Производные

1.

ТЕМА ПАРЫ:
ПОНЯТИЕ ПРОИЗВОДНОЙ.
ФОРМУЛЫ И ПРАВИЛА
ДИФФЕРЕНЦИРОВАНИЯ

2.

НЕМНОГО ИЗ ИСТОРИИ
Производная – одно из фундаментальных понятий
математики, характеризующее скорость изменения
функции в данной точке.
Понятие производной возникло в XXVII веке в
связи с необходимостью решения ряда задач из физики,
механики и математики, но в первую очередь
следующих
двух:
определение
скорости
прямолинейного движения и построения касательной к
кривой.
Раздел математики, в котором изучаются
производные и их применения к исследованию
функций,
называется
дифференциальным
исчислением.

3.

ПРИРАЩЕНИЕ АРГУМЕНТА.
ПРИРАЩЕНИЕ ФУНКЦИИ.
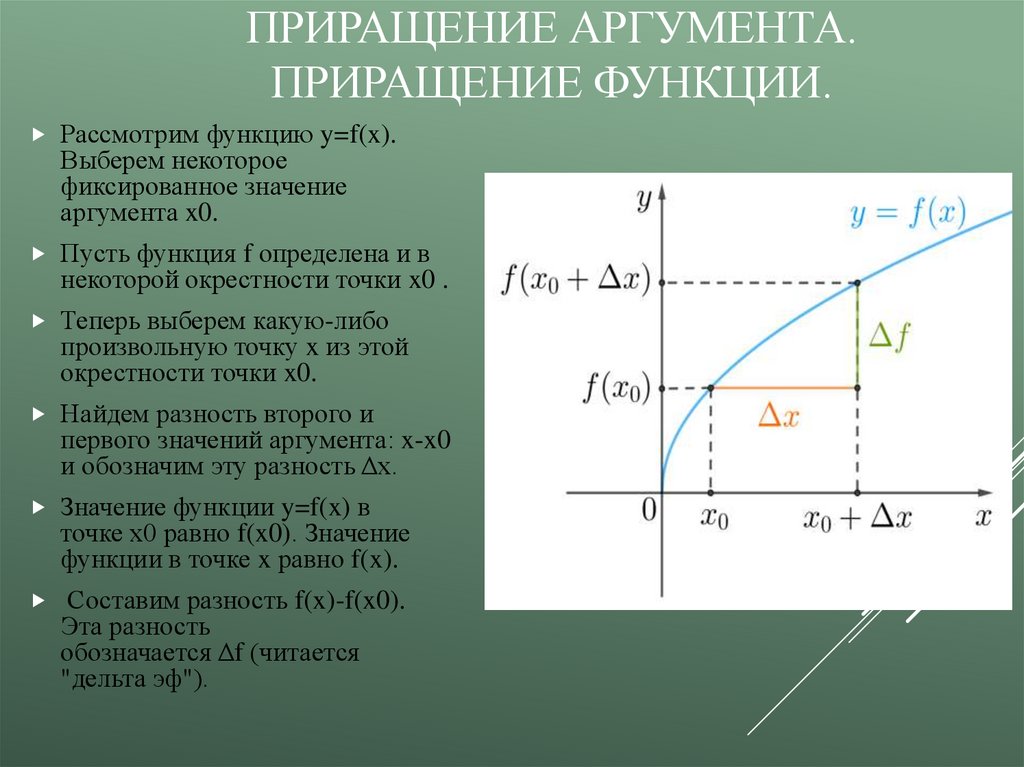
Рассмотрим функцию y=f(x).
Выберем некоторое
фиксированное значение
аргумента x0.
Пусть функция f определена и в
некоторой окрестности точки x0 .
Теперь выберем какую-либо
произвольную точку x из этой
окрестности точки x0.
Найдем разность второго и
первого значений аргумента: x-x0
и обозначим эту разность Δх.
Значение функции y=f(x) в
точке х0 равно f(x0). Значение
функции в точке x равно f(x).
Составим разность f(x)-f(x0).
Эта разность
обозначается Δf (читается
"дельта эф").

4.

Определение:
Пусть функция y=f(x) определена в некоторой окрестности точки x0, а
точка x принадлежит этой окрестности.
Тогда разность Δx=x-x0 называется приращением аргумента в точке x0, а
разность Δf=f(x)-f(x0) называется приращением функции f в точке x0,
соответствующим приращению аргумента Δx.
Приращение аргумента — это величина, равная разности между
конечным и начальным значением аргумента. Обозначается Δx.
Δx=х-х0
Приращение функции — это величина, равная разности между конечным
и начальным значением функции. Обозначается Δy или Δf.
Δf=f(x)-f(x0)
или
Δf=f(x0+ Δx)-f(x0)

5.

Производная простыми словами — это скорость изменения функции. Она
показывает, как и с какой скоростью эта функция меняется в данной конкретной
точке

6.

7.

Дифференцирование функции
!!! Операция отыскания производной называется
дифференцированием.
Чтобы найти производную, надо выражение под
знаком штриха разобрать на составляющие простые
функции и определить, какими
действиями (произведение, сумма, частное) связаны
эти функции. Далее производные элементарных
функций находим в таблице производных, а формулы
производных произведения, суммы и частного - в
правилах дифференцирования.

8.

ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ
ФУНКЦИЙ И ПРАВИЛ
ДИФФЕРЕНЦИРОВАНИЯ

9.

ОСНОВНЫЕ ПРАВИЛА
ДИФФЕРЕНЦИРОВАНИЯ
Если функции u и v дифференцируемы в точке х0,
то справедливы следующие правила:
1. Производная суммы/разности: (u±v)'= u' ± v’
2. Производная произведения: (uv)'=u'v+uv'
4. Производная дроби (u/v)'=(u'v-uv') / v2

10.

ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы
функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «х» равна единице, а
производная синуса - косинусу. Подставляем эти значения в сумму
производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе
слагаемое с постоянным множителем, его можно вынести за знак
производной:

11.

Найдите производные функций
1.
2.

12.

ТЕСТ ПО ТЕМЕ
«ПРОИЗВОДНАЯ ФУНКЦИИ»

13.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ
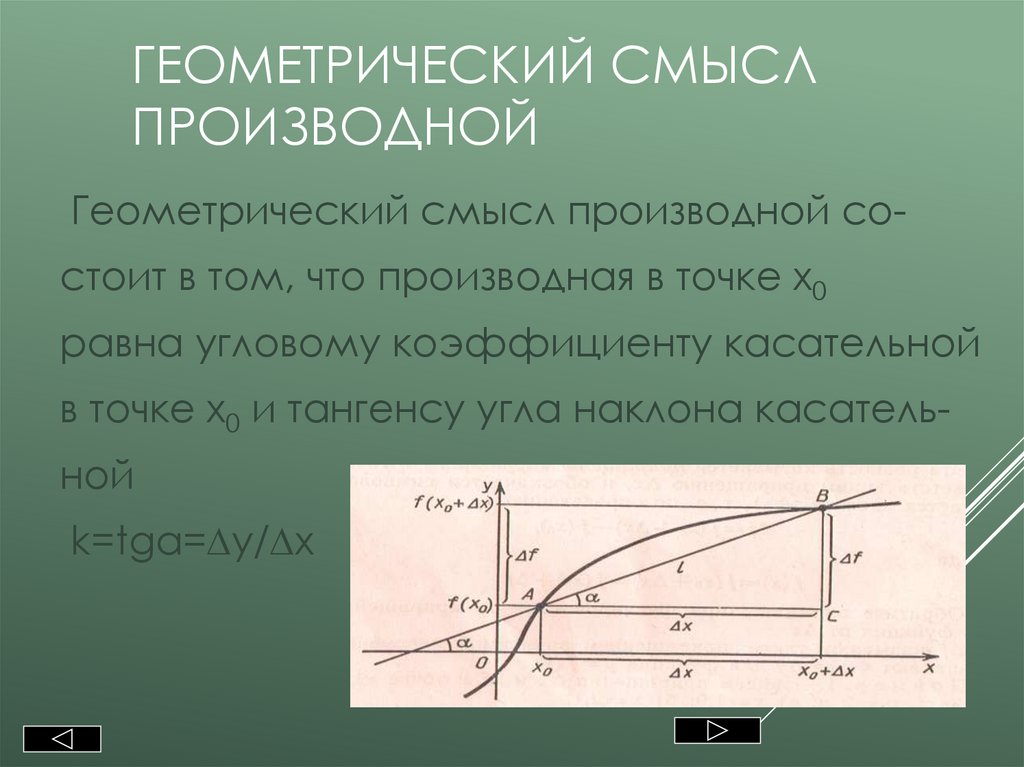
Геометрический смысл производной состоит в том, что производная в точке х0
равна угловому коэффициенту касательной
в точке х0 и тангенсу угла наклона касатель-
ной
k=tgα=∆y/∆x

14.

МЕХАНИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ
(ФИЗИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ)
Механический смысл производной состоит в том, что
производная пути по времени равна мгновенной
скорости в момент времени t0:
S'(t0)=V(t0).

15.

ОТВЕТИМ НА СЛЕДУЮЩИЕ ВОПРОСЫ:
Сформулируйте определение
производной функции?
Как называется математическая операция
нахождения производной функции?
В чем заключается геометрический смысл
производной функции?
Каков физический (механический) смысл
производной?

16.

“УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В
ЗНАНИИ,
НО И В УМЕНИИ ПРИМЕНЯТЬ
ЗНАНИЯ НА ПРАКТИКЕ”
Аристотель