Похожие презентации:
Исследование функции
1. Исследование функции.
2. План:
Определение функции.Область определения. Область значений.
Способы задания функции.
Возрастание, убывание функции.
Ограниченность функции.
Наибольшее, наименьшее значения функции.
Выпуклость, вогнутость функции.
Четность, нечетность функции.
Элементарные функции, их свойства и графики.
3.
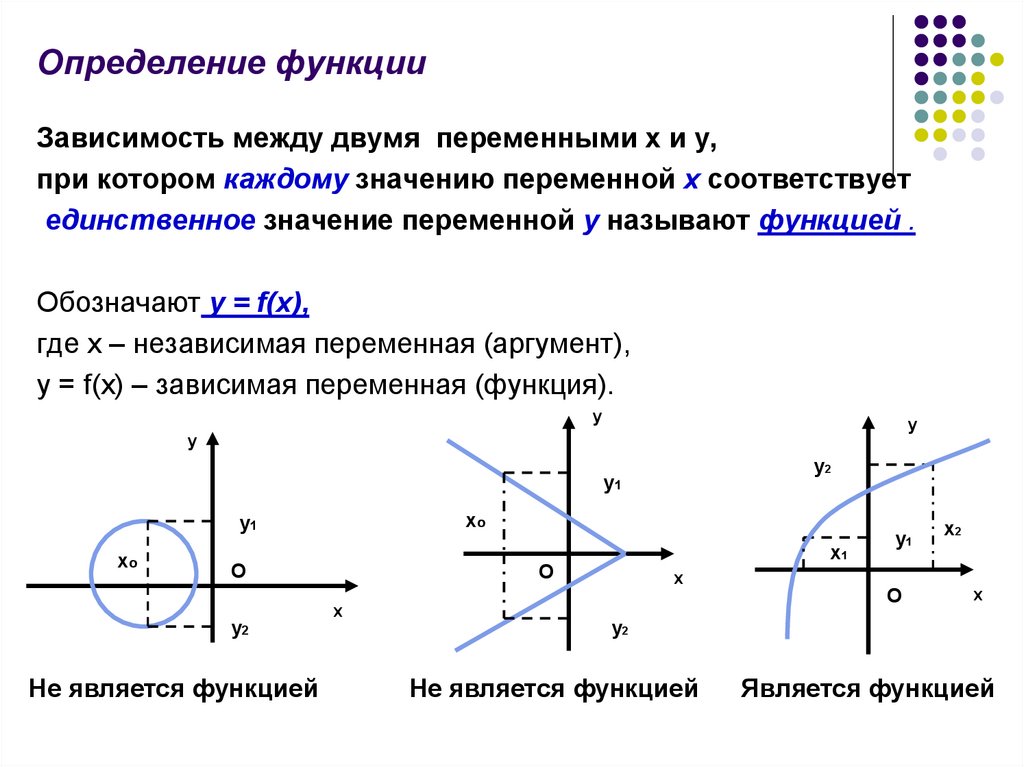
Определение функцииЗависимость между двумя переменными х и у,
при котором каждому значению переменной х соответствует
единственное значение переменной у называют функцией .
Обозначают у = f(х),
где х – независимая переменная (аргумент),
у = f(x) – зависимая переменная (функция).
у
у
у
у2
у1
хо
у1
хо
О
у2
Не является функцией
х1
О
х
х
у1
О
х2
х
у2
Не является функцией
Является функцией
4.
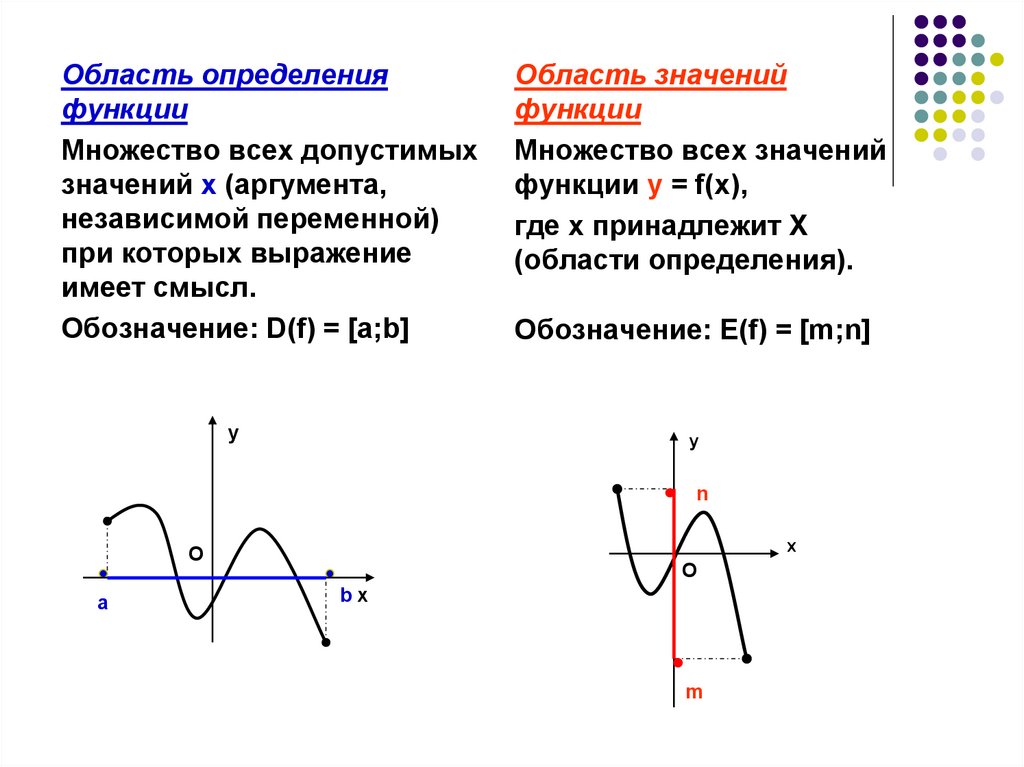
Область определенияфункции
Множество всех допустимых
значений х (аргумента,
независимой переменной)
при которых выражение
имеет смысл.
Обозначение: D(f) = [а;b]
у
Область значений
функции
Множество всех значений
функции у = f(х),
где х принадлежит Х
(области определения).
Обозначение: Е(f) = [m;n]
у
n
х
О
a
О
bх
m
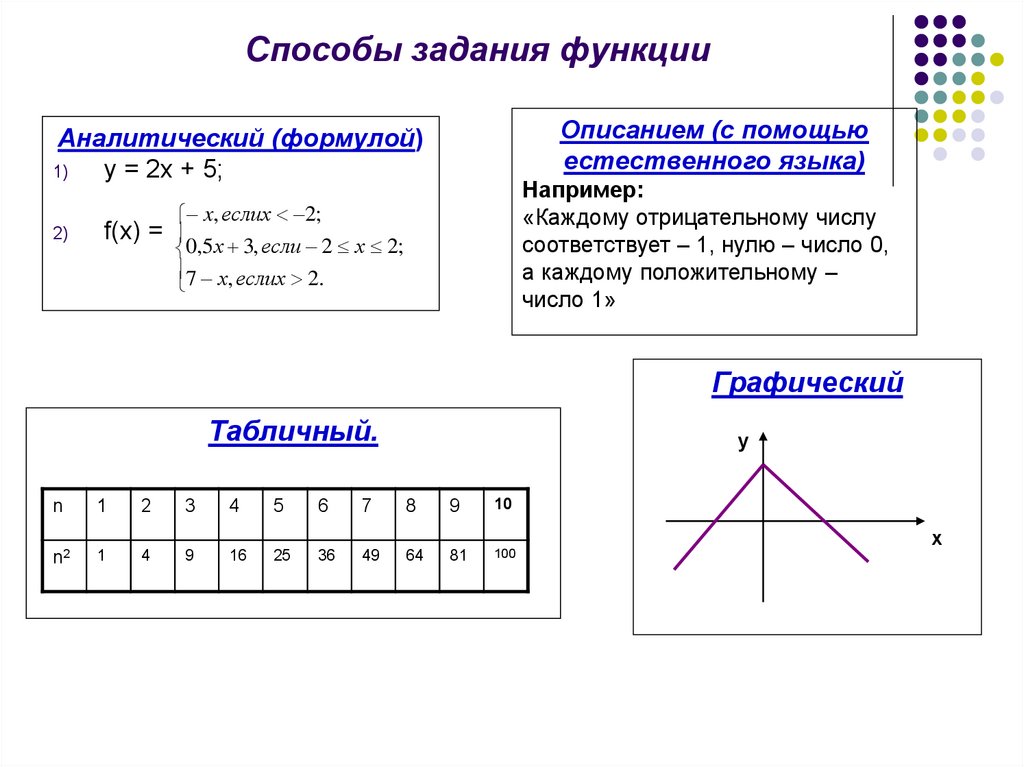
5. Способы задания функции
Описанием (с помощьюестественного языка)
Аналитический (формулой)
1)
у = 2х + 5;
2)
Например:
«Каждому отрицательному числу
соответствует – 1, нулю – число 0,
а каждому положительному –
число 1»
x, еслих 2;
f(x) =
0,5 х 3, если 2 х 2;
7 х, еслих 2.
Графический
Табличный.
у
n
1
2
3
4
5
6
7
8
9
10
n2
1
4
9
16
25
36
49
64
81
100
х
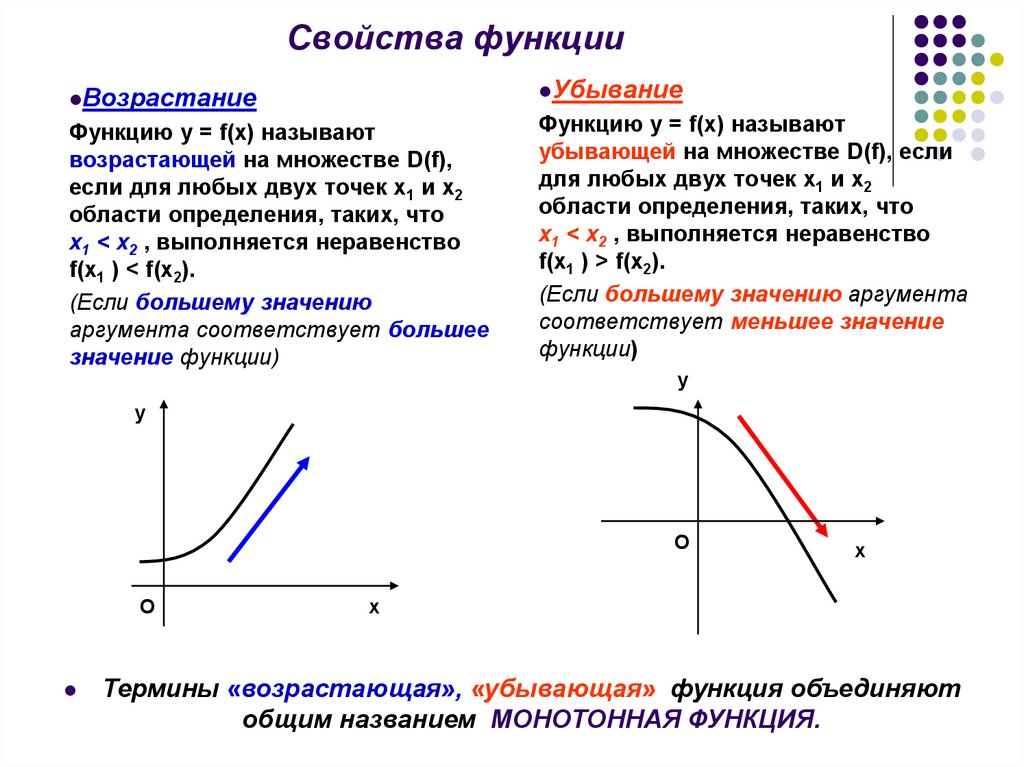
6. Свойства функции
УбываниеВозрастание
Функцию у = f(x) называют
возрастающей на множестве D(f),
если для любых двух точек х1 и х2
области определения, таких, что
х1 < х2 , выполняется неравенство
f(x1 ) < f(x2).
(Если большему значению
аргумента соответствует большее
значение функции)
Функцию у = f(x) называют
убывающей на множестве D(f), если
для любых двух точек х1 и х2
области определения, таких, что
х1 < х2 , выполняется неравенство
f(x1 ) > f(x2).
(Если большему значению аргумента
соответствует меньшее значение
функции)
у
у
О
О
x
x
Термины «возрастающая», «убывающая» функция объединяют
общим названием МОНОТОННАЯ ФУНКЦИЯ.
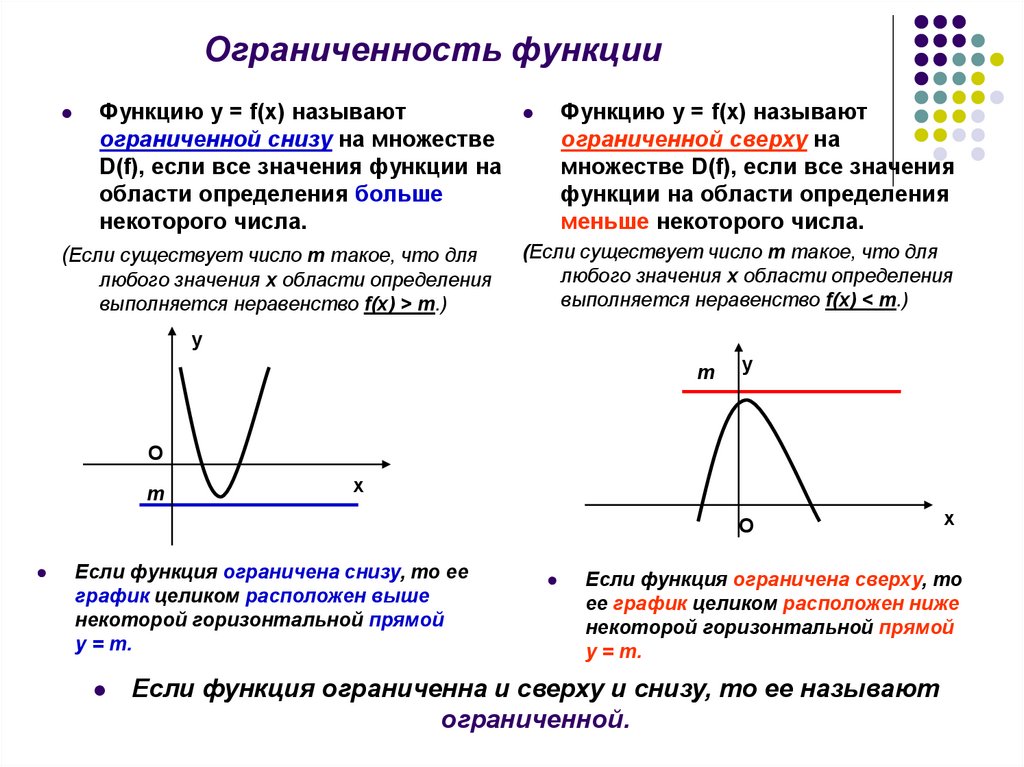
7. Ограниченность функции
Функцию у = f(x) называютограниченной снизу на множестве
D(f), если все значения функции на
области определения больше
некоторого числа.
(Если существует число m такое, что для
любого значения х области определения
выполняется неравенство f(x) > m.)
Функцию у = f(x) называют
ограниченной сверху на
множестве D(f), если все значения
функции на области определения
меньше некоторого числа.
(Если существует число m такое, что для
любого значения х области определения
выполняется неравенство f(x) < m.)
у
m
у
О
m
x
О
Если функция ограничена снизу, то ее
график целиком расположен выше
некоторой горизонтальной прямой
у = m.
x
Если функция ограничена сверху, то
ее график целиком расположен ниже
некоторой горизонтальной прямой
у = m.
Если функция ограниченна и сверху и снизу, то ее называют
ограниченной.
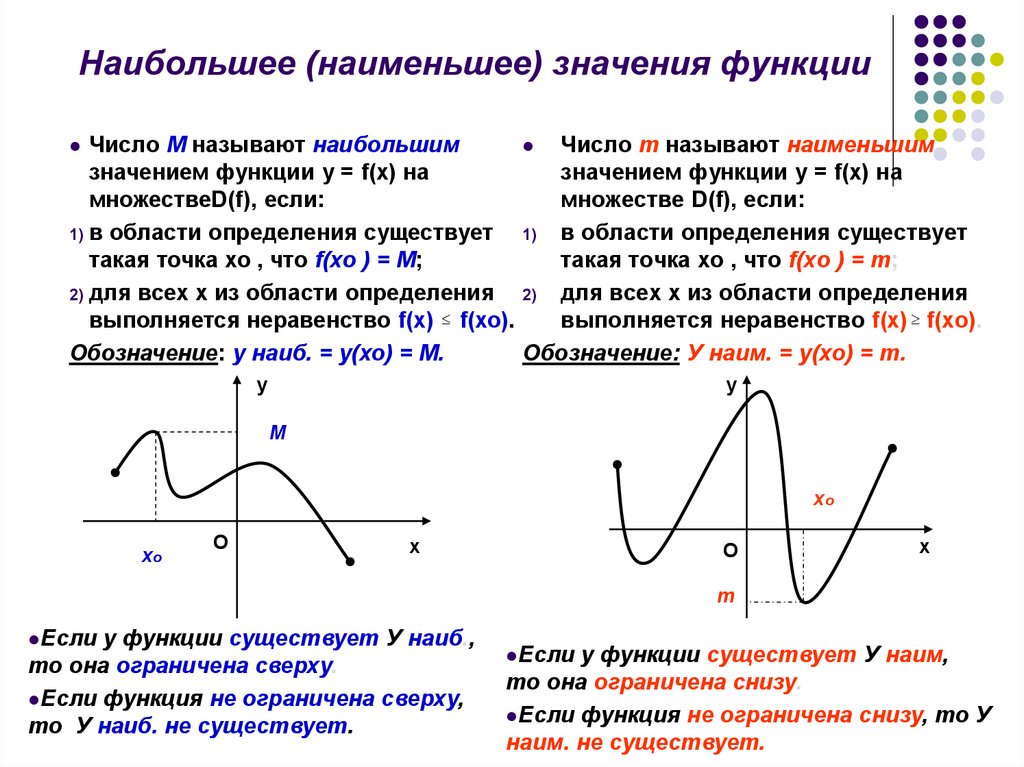
8. Наибольшее (наименьшее) значения функции
Число M называют наибольшимЧисло m называют наименьшим
значением функции у = f(x) на
значением функции у = f(x) на
множествеD(f), если:
множестве D(f), если:
1) в области определения существует
1)
в области определения существует
такая точка хо , что f(хо ) = M;
такая точка хо , что f(хо ) = m;
2) для всех х из области определения
2)
для всех х из области определения
выполняется неравенство f(x) f(хо).
выполняется неравенство f(x) f(хо).
Обозначение: у наиб. = у(хо) = M.
Обозначение: У наим. = у(хо) = m.
у
у
M
хо
хо
О
х
О
х
m
Если у функции существует У наиб.,
то она ограничена сверху.
Если функция не ограничена сверху,
то У наиб. не существует.
Если у функции существует У наим,
то она ограничена снизу.
Если функция не ограничена снизу, то У
наим. не существует.
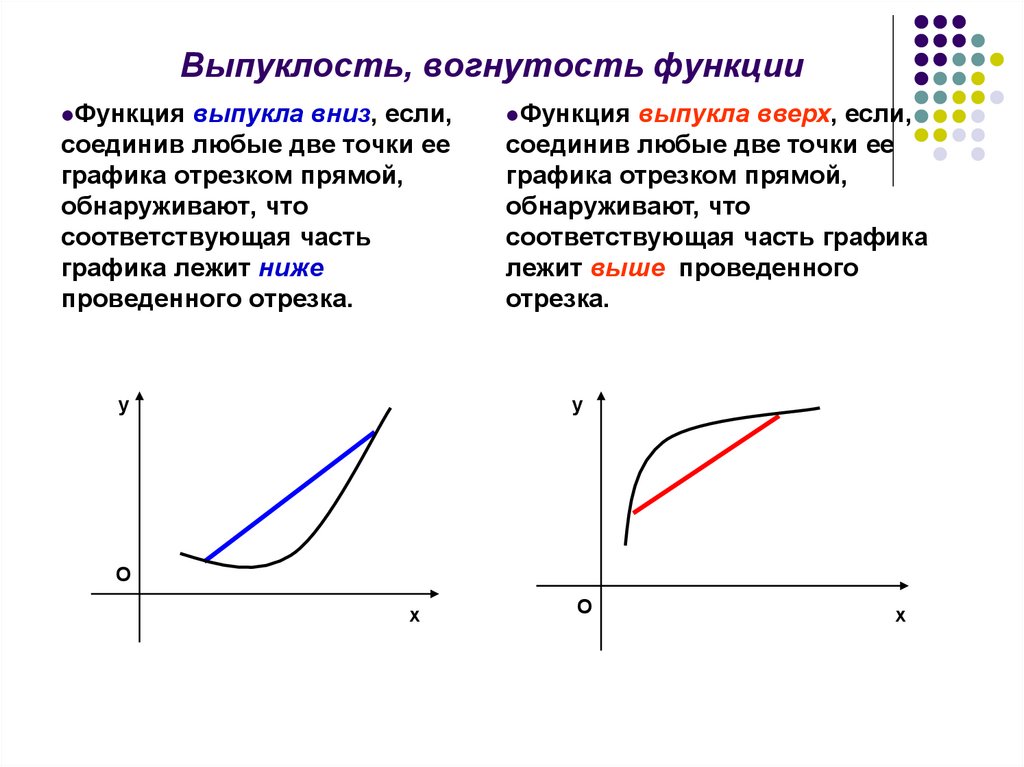
9. Выпуклость, вогнутость функции
Функция выпукла вниз, если,Функция выпукла вверх, если,
соединив любые две точки ее
графика отрезком прямой,
обнаруживают, что
соответствующая часть
графика лежит ниже
проведенного отрезка.
соединив любые две точки ее
графика отрезком прямой,
обнаруживают, что
соответствующая часть графика
лежит выше проведенного
отрезка.
у
у
О
x
О
x
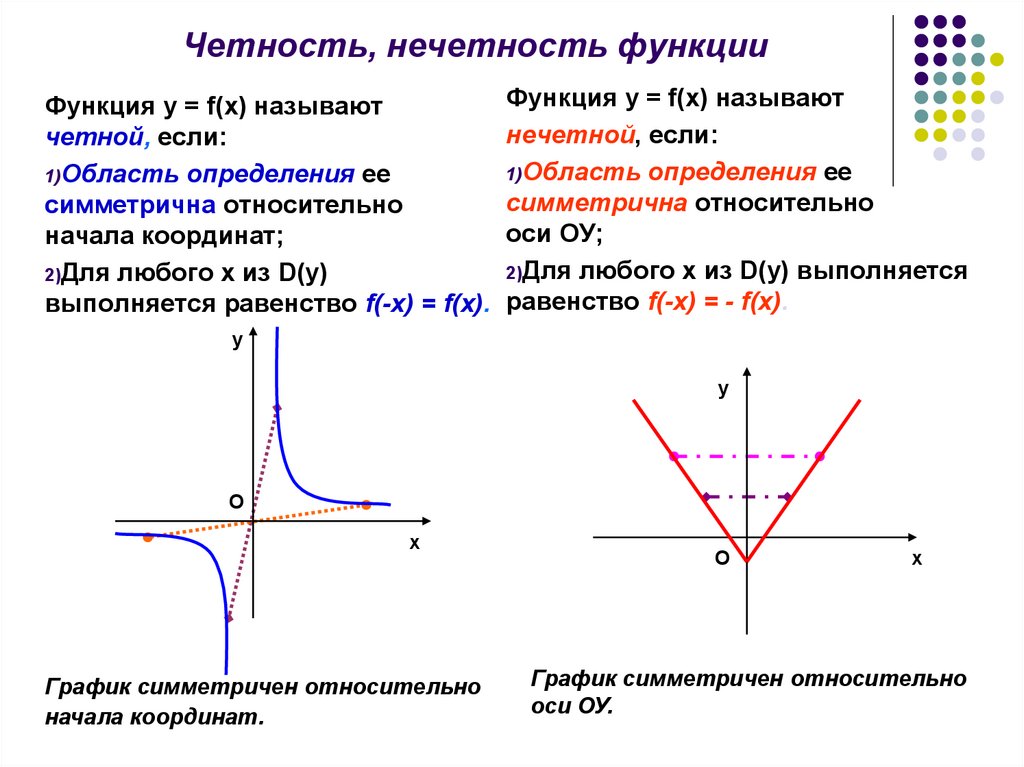
10. Четность, нечетность функции
Функция у = f(х) называютФункция у = f(х) называют
нечетной, если:
четной, если:
1)Область определения ее
1)Область определения ее
симметрична относительно
симметрична относительно
оси ОУ;
начала координат;
2)Для любого х из D(у) выполняется
2)Для любого х из D(у)
выполняется равенство f(-x) = f(x). равенство f(-x) = - f(x).
у
у
О
x
График симметричен относительно
начала координат.
О
x
График симметричен относительно
оси ОУ.
11. Алгоритм исследования функции
Область определения.Область значений.
Четность, нечетность функции.
Возрастание, убывание функции.
Ограниченность функции.
Наибольшее, наименьшее значения функции.
Непрерывность функции.
Выпуклость, вогнутость функции.
12. Линейная функция
y kx m(k 0)K>0
у
1. D(f) = R;
2. Не является ни четной ни
нечетной;
3. Если k > 0, возрастает,
если k < 0 убывает;
4. Не ограничена ни снизу, ни
сверху;
5. Нет ни наибольшего, ни
наименьшего значения;
6. Функция непрерывна;
7. Е( f ) ,0 0,
8. Не имеет выпуклости.
m
О
х
у
K<0
m
О
х
13. Функция
kФункция y
x
1. D( f ) ,0 0,
2. Нечетная функция;
3. Если k > 0, то функция убывает на D(f),
если k < 0, то функция возрастает на D(f);
4. Не ограничена ни сверху, ни снизу;
5. Нет ни наименьшего, ни наибольшего значений;
6. Функция терпит разрыв в точке х = 0;
7. Е( f ) ,0 0,
8. Если k > 0, то функция выпукла вверх при х < 0,
и выпукла вниз при х > 0;
Если k < 0, то функция выпукла вверх при х > 0,
и выпукла вниз при х < 0.
у
K>0
О
x
у
K<0
О
х
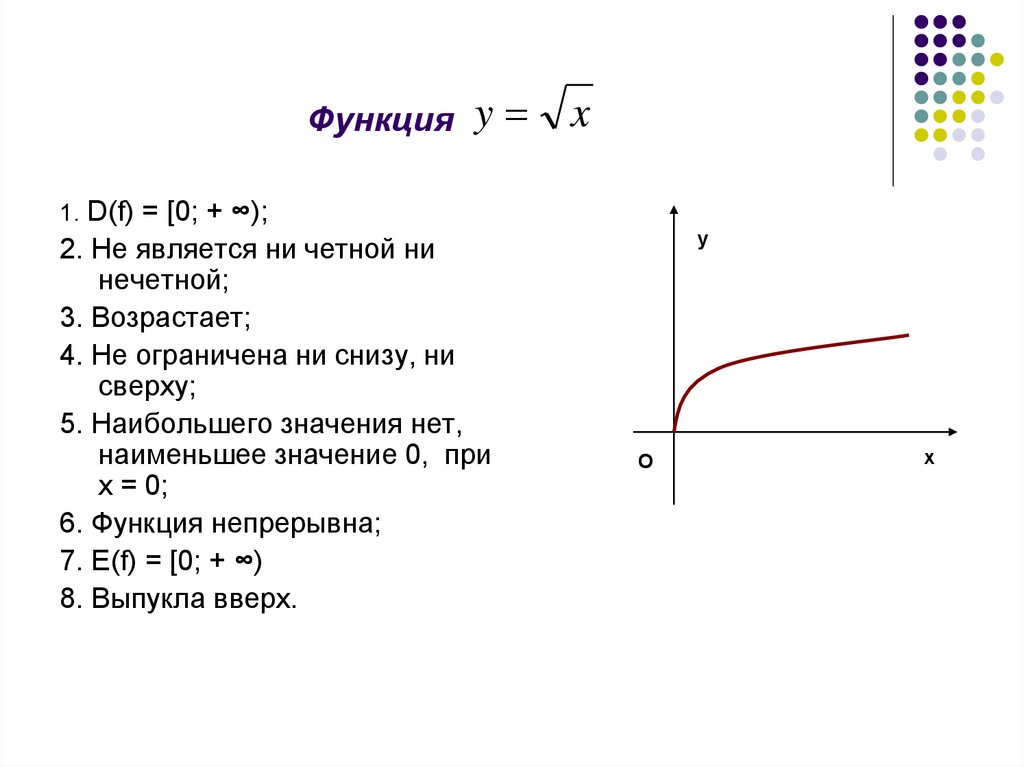
14. Функция
yx
1. D(f) = [0; + ∞);
2. Не является ни четной ни
нечетной;
3. Возрастает;
4. Не ограничена ни снизу, ни
сверху;
5. Наибольшего значения нет,
наименьшее значение 0, при
х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вверх.
у
О
х
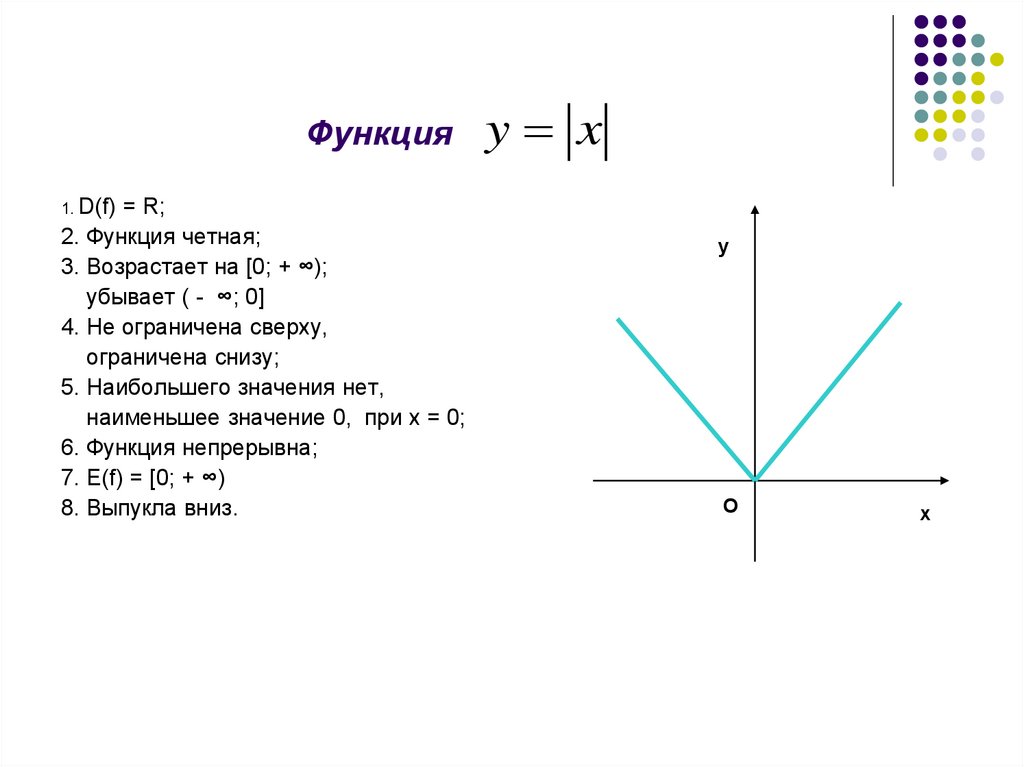
15. Функция
y x1. D(f) = R;
2. Функция четная;
3. Возрастает на [0; + ∞);
убывает ( - ∞; 0]
4. Не ограничена сверху,
ограничена снизу;
5. Наибольшего значения нет,
наименьшее значение 0, при х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вниз.
у
О
х
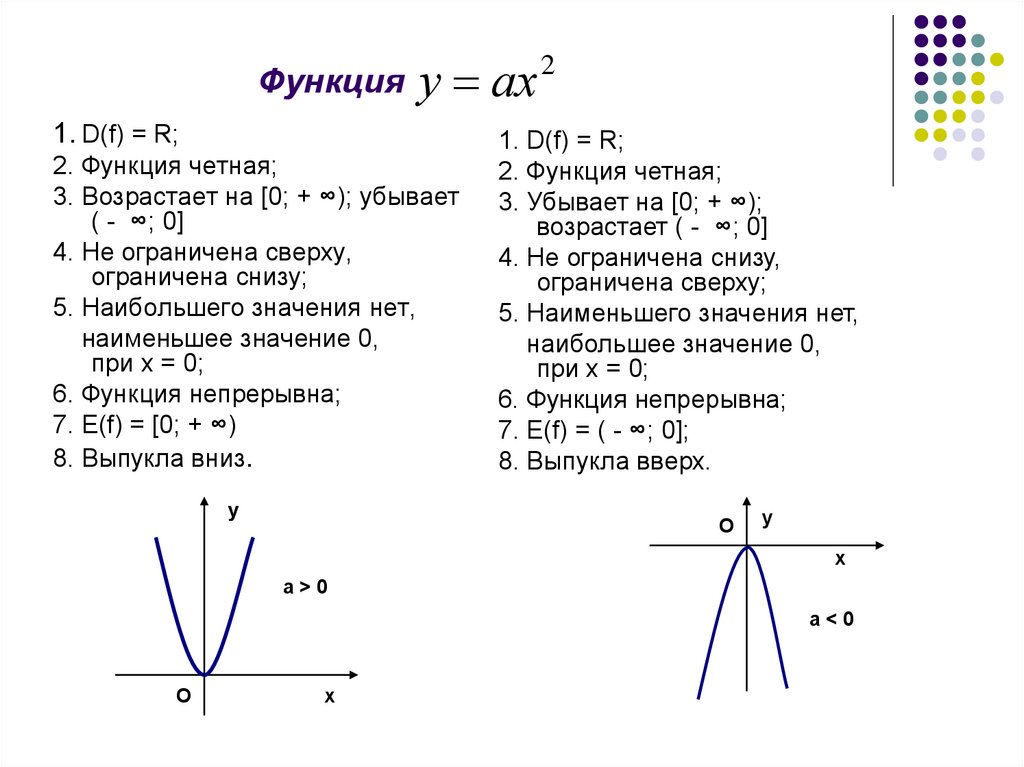
16. Функция
у ах1. D(f) = R;
2. Функция четная;
3. Возрастает на [0; + ∞); убывает
( - ∞; 0]
4. Не ограничена сверху,
ограничена снизу;
5. Наибольшего значения нет,
наименьшее значение 0,
при х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вниз.
у
2
1. D(f) = R;
2. Функция четная;
3. Убывает на [0; + ∞);
возрастает ( - ∞; 0]
4. Не ограничена снизу,
ограничена сверху;
5. Наименьшего значения нет,
наибольшее значение 0,
при х = 0;
6. Функция непрерывна;
7. Е(f) = ( - ∞; 0];
8. Выпукла вверх.
О
у
х
a>0
a<0
О
х




 Математика
Математика








