Лекция № 4-24 чтение

1.

Мясоедов
Сергей Александрович
Курс лекций
"НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ"

2.

Лекция 4
Содержание:
Коническая и цилиндрическая поверхность
Прямой винтовой коноид
Линейчатые поверхности вращения
Сечения конической поверхности вращения
Поверхности вращения общего вида
Параболоид вращения
Однополостный и двуполостный гиперболоиды
вращения
Эллипсоид вращения
Сферическая поверхность, поверхности тора
Проецирующие поверхности
Методика решения главных позиционных задач

3.

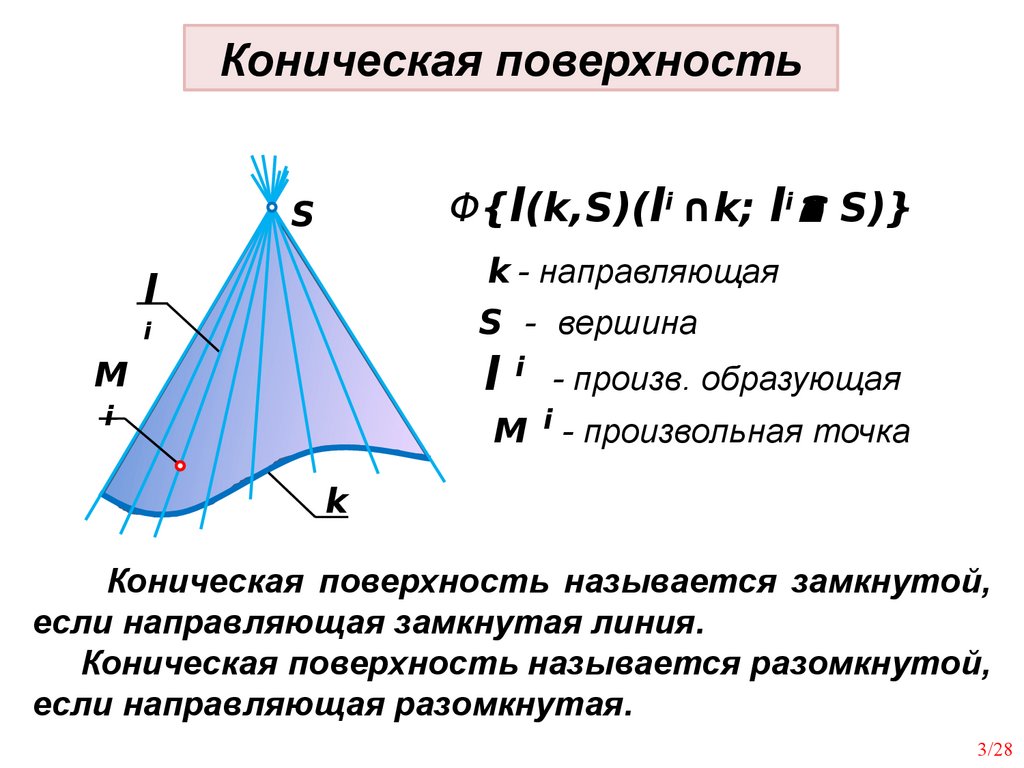
Коническая поверхность
Φ{l(k,S)(li ∩k; li S)}
S
k - направляющая
l
S - вершина
i
l i - произв. образующая
M
i
M i - произвольная точка
k
Коническая поверхность называется замкнутой,
если направляющая замкнутая линия.
Коническая поверхность называется разомкнутой,
если направляющая разомкнутая.
3/28

4.

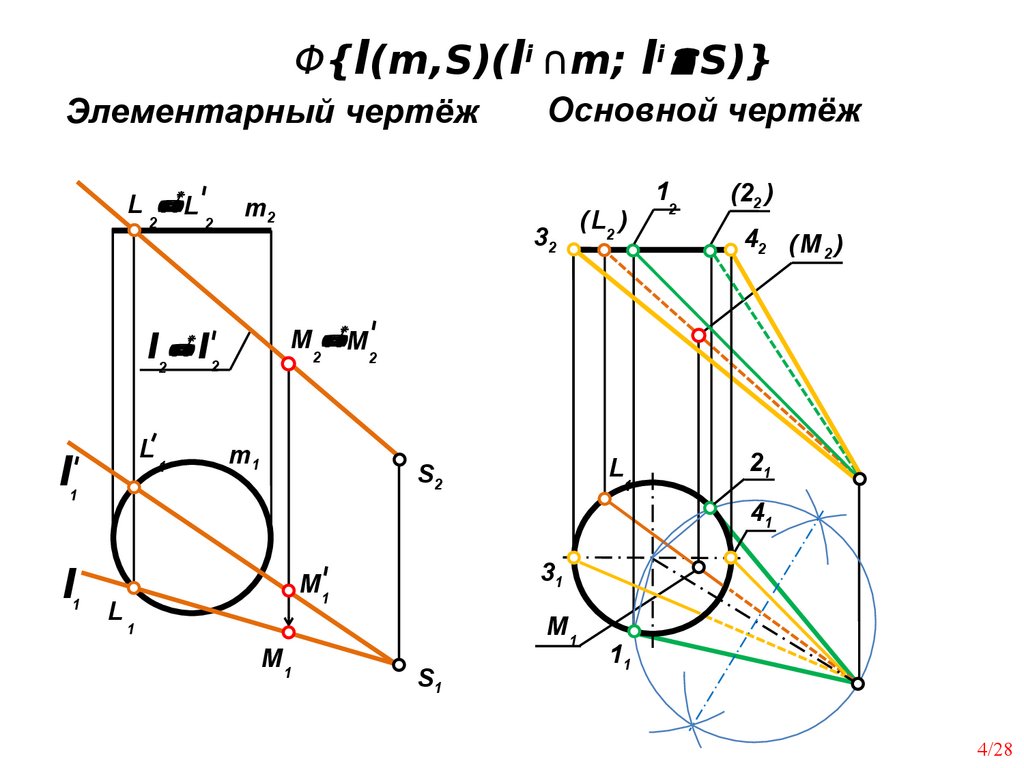
Φ{l(m,S)(li ∩m; li S)}
Элементарный чертёж
L L
2
2
m2
L
l
1
32
M M
l2 l 2
2
m1
1
( L2 )
1
2
(22 )
42 ( M 2 )
2
L
S2
1
l
Основной чертёж
1
21
41
L
31
M1
M1
1
M1
S1
11
4/28

5.

Цилиндрическая поверхность
Φ{l(l,k)(li ∩k;li ııl)}
li
k - направляющая
M
l - образующая
i
l
l i
- произвольная образующая
M i - произвольная точка
k
Цилиндрическая поверхность называется
замкнутой, если направляющая замкнутая линия.
Цилиндрическая поверхность называется
разомкнутой, если направляющая разомкнутая
линия.
5/28

6.

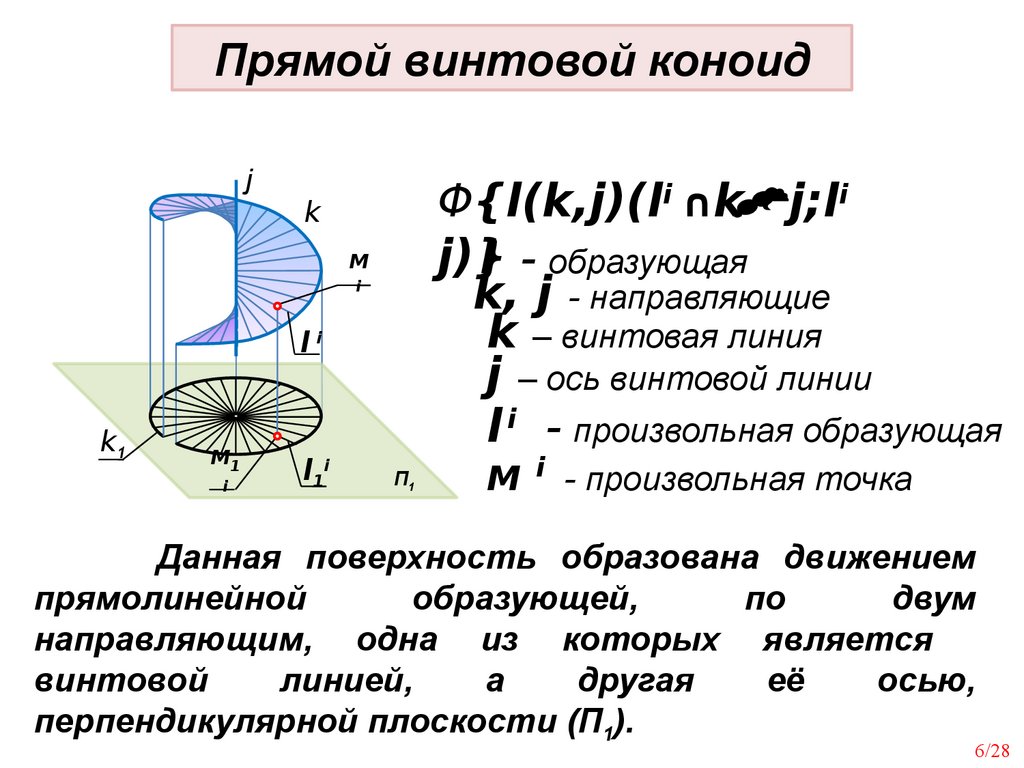
Прямой винтовой коноид
j
Φ{l(k,j)(li ∩k
j;li
j)}
l - образующая
k, j - направляющие
k – винтовая линия
j – ось винтовой линии
l i - произвольная образующая
k
M
i
li
k1
M1
i
l1i
П1
M i - произвольная точка
Данная поверхность образована движением
прямолинейной
образующей,
по
двум
направляющим, одна из которых является
винтовой
линией,
а
другая
её
осью,
перпендикулярной плоскости (П1).
6/28

7.

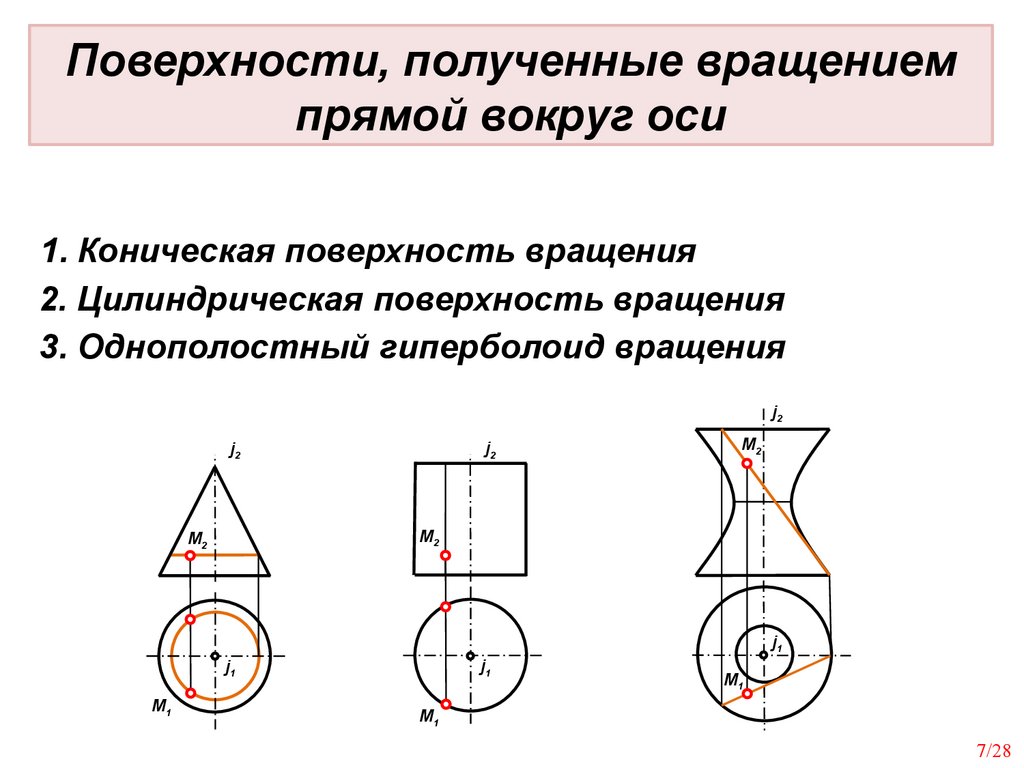
Поверхности, полученные вращением
прямой вокруг оси
1. Коническая поверхность вращения
2. Цилиндрическая поверхность вращения
3. Однополостный гиперболоид вращения
j2
j2
j2
M2
M2
M2
j1
j1
j1
M1
M1
M1
7/28

8.

1. Коническая поверхность вращения
Φ{l(l,j,l
∩ j)(li=l
Данная линейчатая
j)} поверхность образована
вращением прямолинейной образующей вокруг
неподвижной оси, с которой она пересекается.
2. Цилиндрическая поверхность вращения
Φ{l(l,j,l j)(li=l
Данная линейчатая
j)} поверхность образована
вращением прямолинейной образующей вокруг
неподвижной оси, с которой она параллельна.
3. Однополостный гиперболоид
Φ{l(l,j,l j)(li=l j)}
Данная линейчатая поверхность образована
вращением прямолинейной образующей вокруг
неподвижной оси, с которой она скрещивается.
8/28

9.

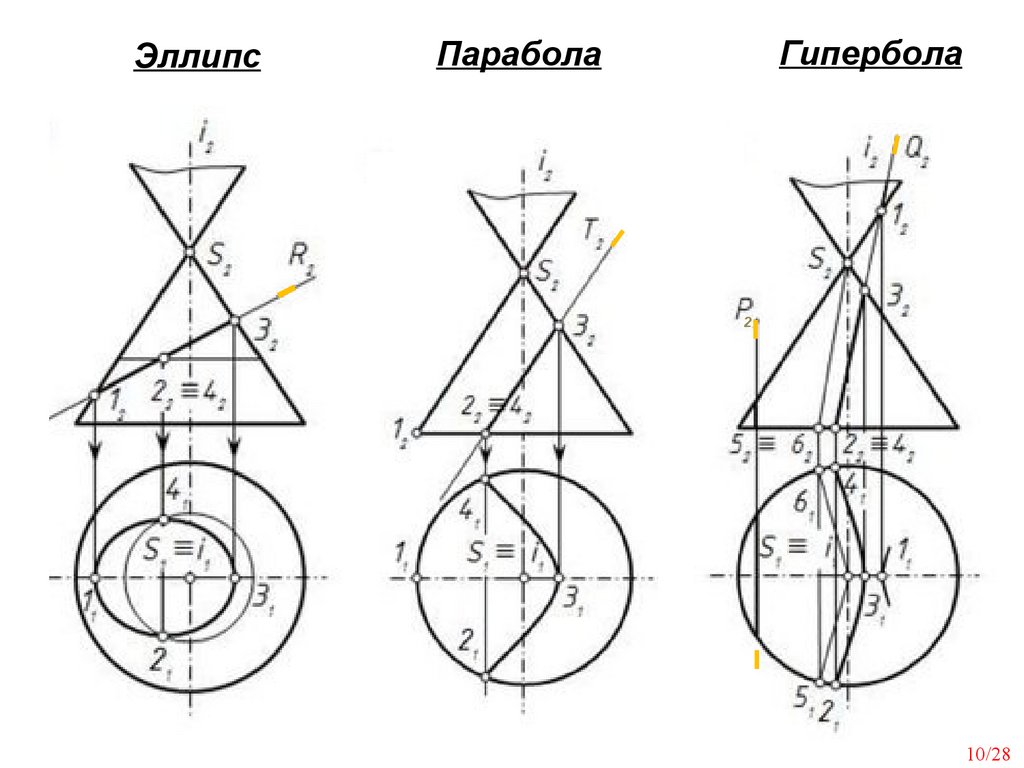
Сечения конической поверхности
вращения плоскостью
а) Окружность – секущая плоскость перпендикулярна оси
конуса
б) Эллипс – секущая плоскость наклонена к оси конуса и
пересекает все его образующие
в) Парабола – секущая плоскость параллельна одной образующей
конуса
г) Гипербола – секущая плоскость параллельна двум образующим
конуса
д) Прямые – секущая плоскость проходит через вершину и
пересекает конус
а)
б)
в)
г)
д)
9/28

10.

Эллипс
Гипербола
Парабола
2
10/28

11.

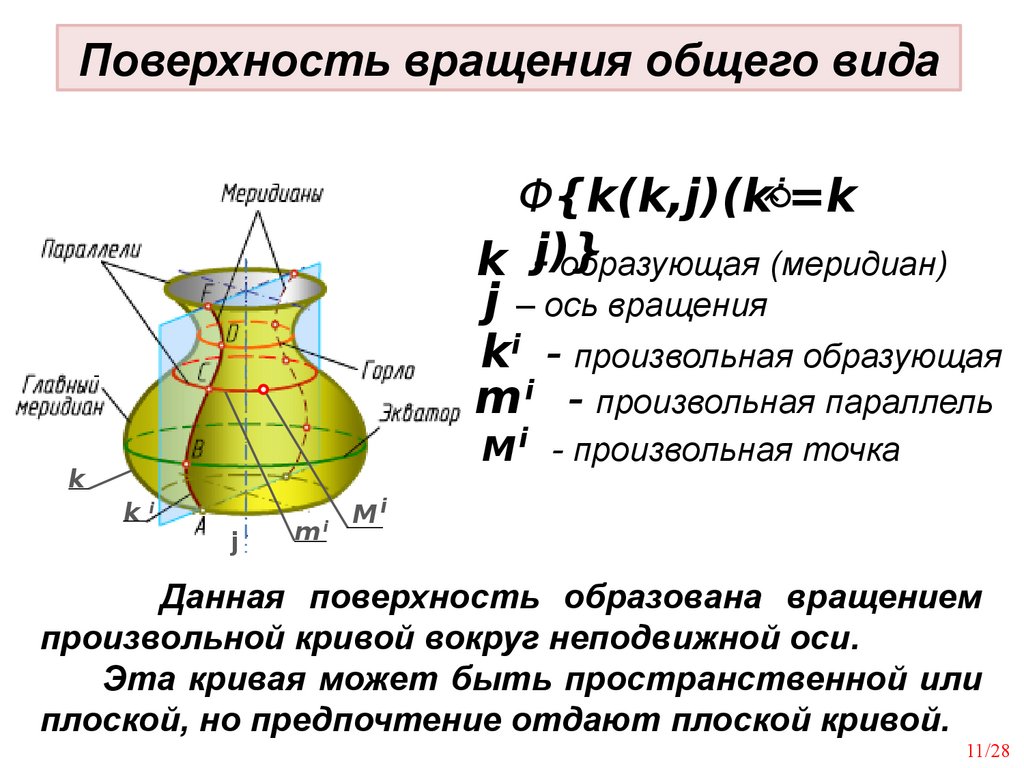
Поверхность вращения общего вида
Φ{k(k,j)(k i =k
k -j)}
образующая (меридиан)
j – ось вращения
ki - произвольная образующая
m i - произвольная параллель
M i - произвольная точка
k
kС i
М
j
m
i
Mi
Данная поверхность образована вращением
произвольной кривой вокруг неподвижной оси.
Эта кривая может быть пространственной или
плоской, но предпочтение отдают плоской кривой.
11/28

12.

Все поверхности вращения могут быть заданы
окружностями (параллелями), центры которых
двигаются по неподвижной оси, при этом касаясь
другой направляющей (меридиана).
Проводить окружности (параллели) гораздо
проще, чем строить повернутые положения
меридиан, для которых необходимо достаточно
много точек, соединяемых с помощью лекал.
В связи с этим на поверхностях вращения
целесообразно строить произвольные окружности
(параллели), на которых можно брать произвольные
точки.
12/28

13.

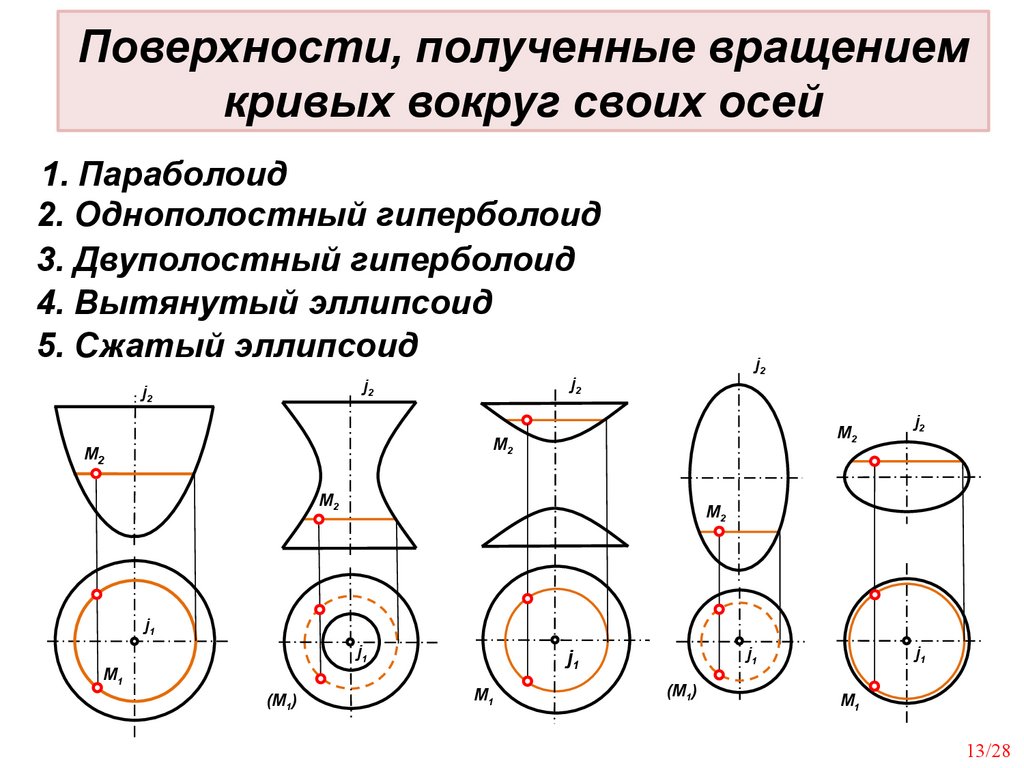
Φ{m(m,j;m∩j)(mi=m j)}.
Поверхности, полученные вращением
кривых вокруг своих осей
1. Параболоид
2. Однополостный гиперболоид
3. Двуполостный гиперболоид
4. Вытянутый эллипсоид
5. Сжатый эллипсоид
j2
j2
j2
j2
M2
M2
M2
M2
j2
M2
j1
j1
M1
(M1)
M1
j1
j1
j1
(M1)
M1
13/28

14.

1. Параболоид вращения Φ{k(k,j)(k i =k
k j)}
- образующая (парабола)
j – ось параболы
Поверхность образована вращением параболы
(образующей) вокруг своей оси.
2. Однополостный гиперболоид Φ{k(k,j)(k i =k
j)} (гипербола)
k - образующая
j – мнимая ось гиперболы
Поверхность образована вращением гиперболы
(образующей) вокруг её мнимой оси.
3. Двуполостный гиперболоид Φ{k(k,j)(k i =k
k - образующая j)}
(гипербола)
j – действительная ось гиперболы
Поверхность образована вращением гиперболы
(образующей) вокруг своей действительной оси.
14/28

15.

4. Вытянутый эллипсоид Φ{k(k,j)(k i =k
j)}
k - образующая (эллипс)
j – большая ось эллипса
Поверхность образована вращением эллипса
(образующей) вокруг её большой оси.
5. Сжатый эллипсоид Φ{k(k,j)(k i =k
k - образующая
j)} (эллипс)
j – малая ось эллипса
Поверхность образована вращением эллипса
(образующей) вокруг её малой оси.
15/28

16.

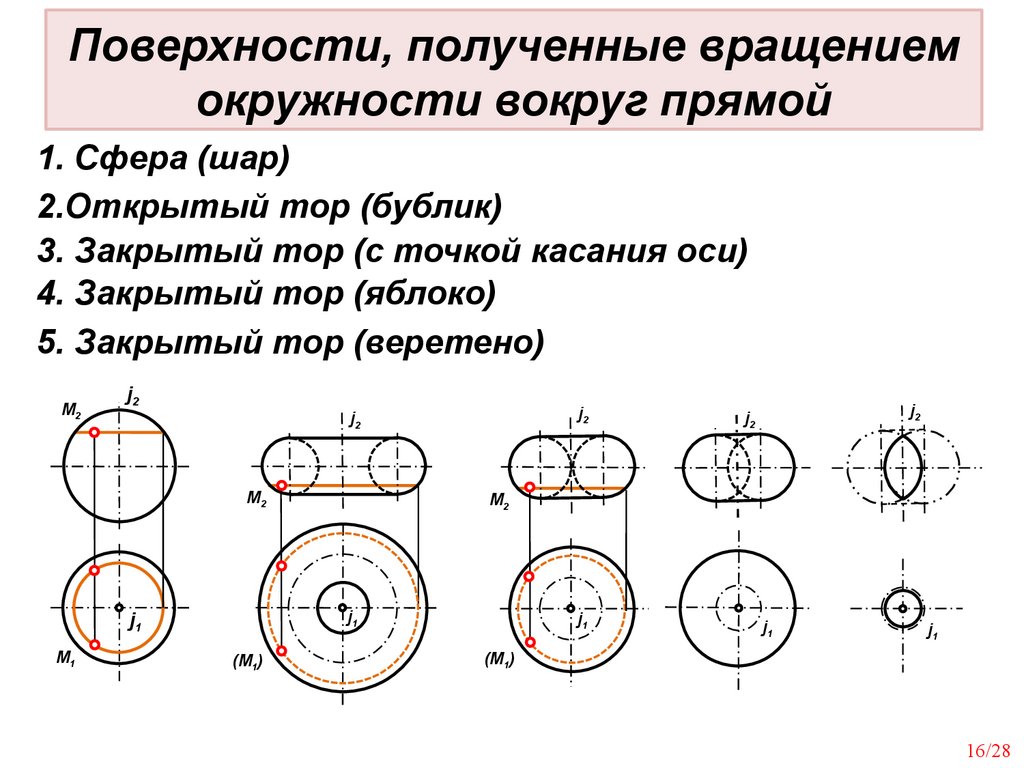
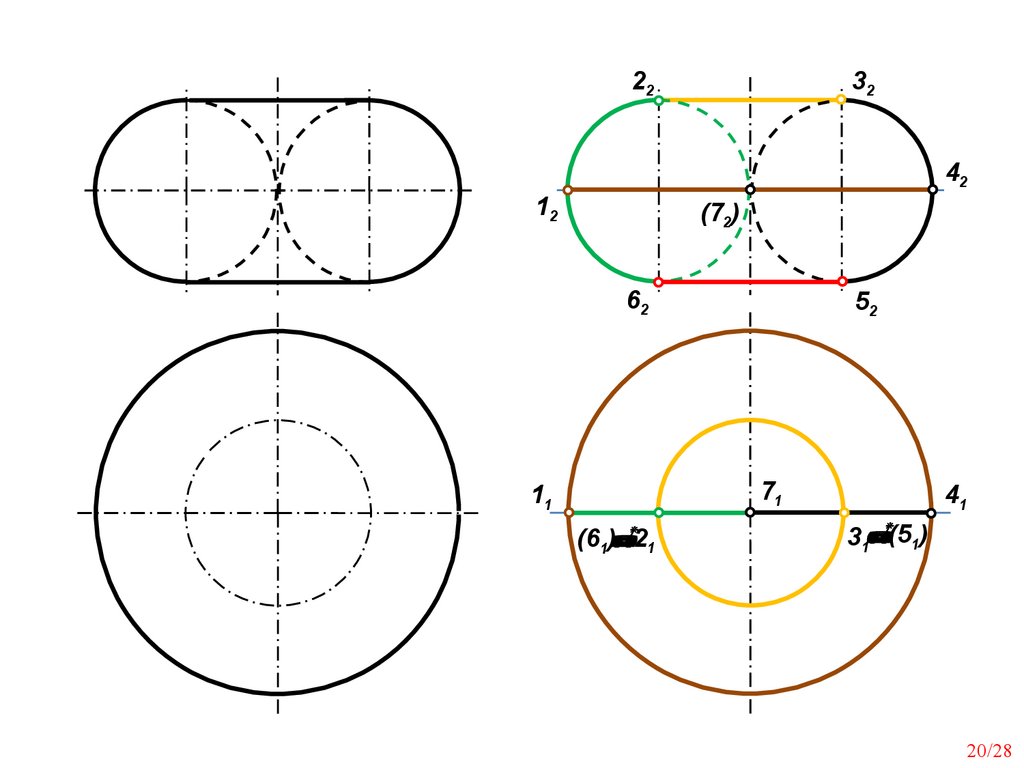
Φ{m(m,j;m∩j)(mi=m j)}.
Поверхности, полученные вращением
окружности вокруг прямой
1. Сфера (шар)
2.Открытый тор (бублик)
3. Закрытый тор (с точкой касания оси)
4. Закрытый тор (яблоко)
5. Закрытый тор (веретено)
M2
j2
M2
(M1)
j2
j2
M2
j1
j1
M1
j2
j2
j1
j1
j1
(M1)
16/28

17.

1. Сфера (шар)
Φ{m(m,j; С m j)(m i =m
j)}m - образующая (окружность)
j – диаметр окружности
Сm– центр окружности
Поверхность образована вращением окружности
(образующей) вокруг её диаметра.
2. Открытый тор (бублик)
Φ{m(m,j;m j Г;m
∩ j)(mi=m j)}
m - образующая (окружность)
j – ось вращения
Г – плоскость, содержащая ось и
Поверхность
образована вращением окружности
окружность
(образующей) вокруг оси, лежащей в плоскости
окружности, но не пересекающую её.
17/28

18.

3. Закрытый тор (с точкой касания оси)
Φ{m(m,j;m j)(m i =m
j)}m - образующая (окружность)
j – ось вращения
Поверхность образована вращением окружности
(образующей) вокруг оси, лежащей в плоскости
окружности и касающуюся её.
4. Закрытый тор (яблоко)
5. Закрытый тор (веретено)
Φ{m(m,j;m
j)(m i =m
∩
j)}m - образующая (окружность)
j – ось вращения
Поверхности образованы вращением окружности
(образующей) вокруг оси, лежащей в плоскости
окружности и пересекающую её.
18/28

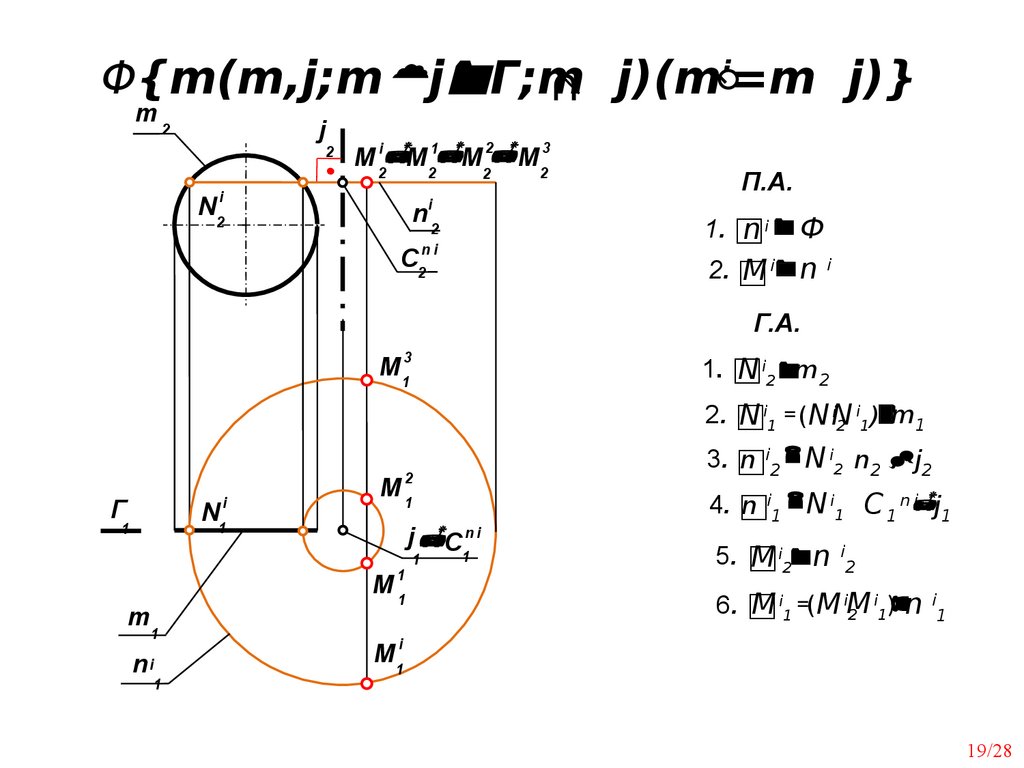
19.

Φ{m(m,j;m j Г;m
∩ j)(mi=m j)}
m
j
2
2
2
3
M 2i M21 M2 M2
i
N2
i
n2
П.А.
1.
ni Ф
С2n i
2.
M i n i
Г.А.
M 13
1.
N i2 m2
i i
2.
m1
N i1 = ( N N
2 1)
i
N1
1
m
n
M 21
j С n i
M 11
1
i
1
1
1
i
4.
n i1 N i1 С 1 n
j1
5.
M i2 n i2
i
i
6.
M i1 =(M iM
2 1) n 1
Г
3.
n i2 N i2 n2 j2
M1i
19/28

20.

22
32
42
12
(72)
62
52
71
11
(61) 21
41
31 (51)
20/28

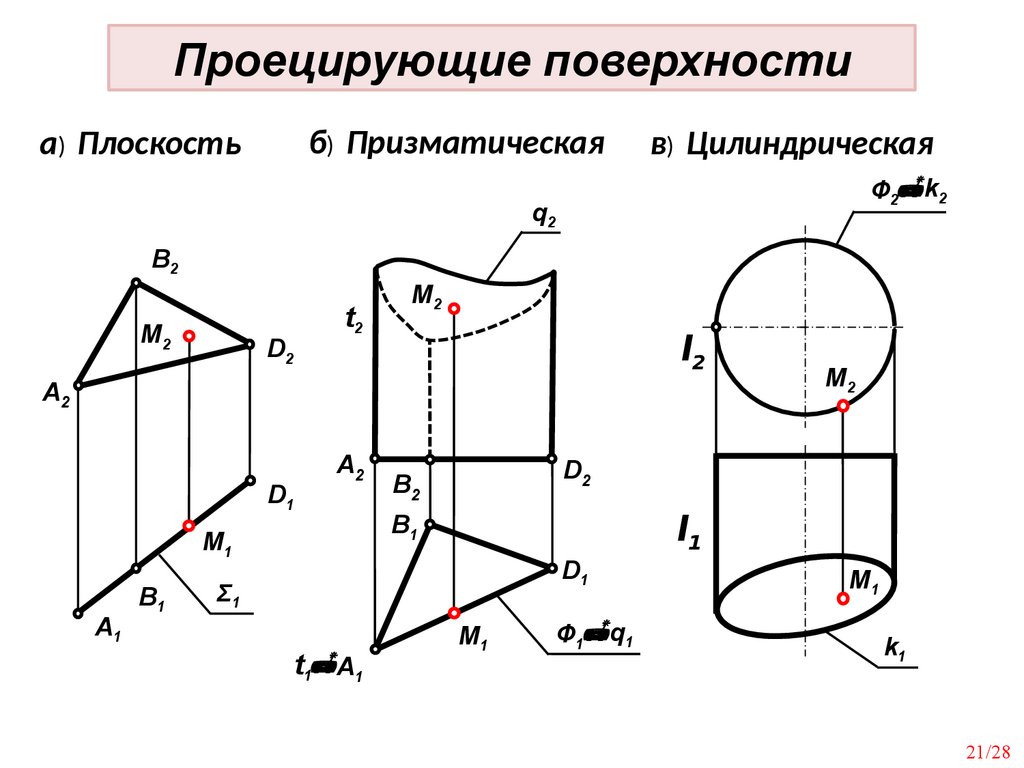
21.

Проецирующие поверхности
б) Призматическая
а) Плоскость
в) Цилиндрическая
Ф2 k2
q2
B2
M2
t2
D2
M2
l2
A2
D1
A2
M1
A1
B1
D2
B2
B1
D1
Ʃ1
t1 A1
M2
M1
Ф1 q1
l1
M1
k1
21/28

22.

Главные позиционные задачи (ГПЗ)
1. Задачи на пересечение линии и поверхности.
2. Задачи на пересечение поверхностей.
Методика решения главных позиционных задач
зависит от того, являются геометрические образы
(ГО) проецирующими или нет.
Выделяются три случая расположения ГО
относительно плоскостей проекций:
1. Оба ГО занимают проецирующее положение
относительно плоскостей проекций.
2. Один ГО не проецирующий, а другой проецирующий.
3. Оба ГО не проецирующие.
22/28

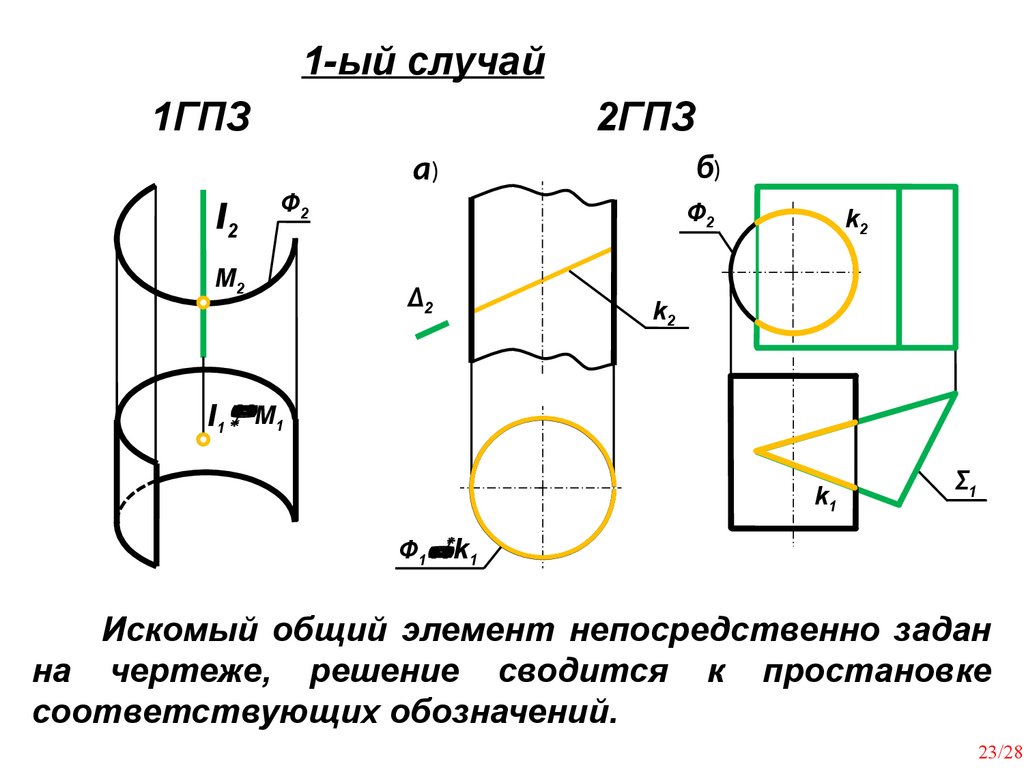
23.

1-ый случай
1ГПЗ
2ГПЗ
Ф2
l2
M2
Ф2
∆2
k2
k2
l1
б)
а)
M1
k1
Ʃ1
Ф1 k1
Искомый общий элемент непосредственно задан
на чертеже, решение сводится к простановке
соответствующих обозначений.
23/28

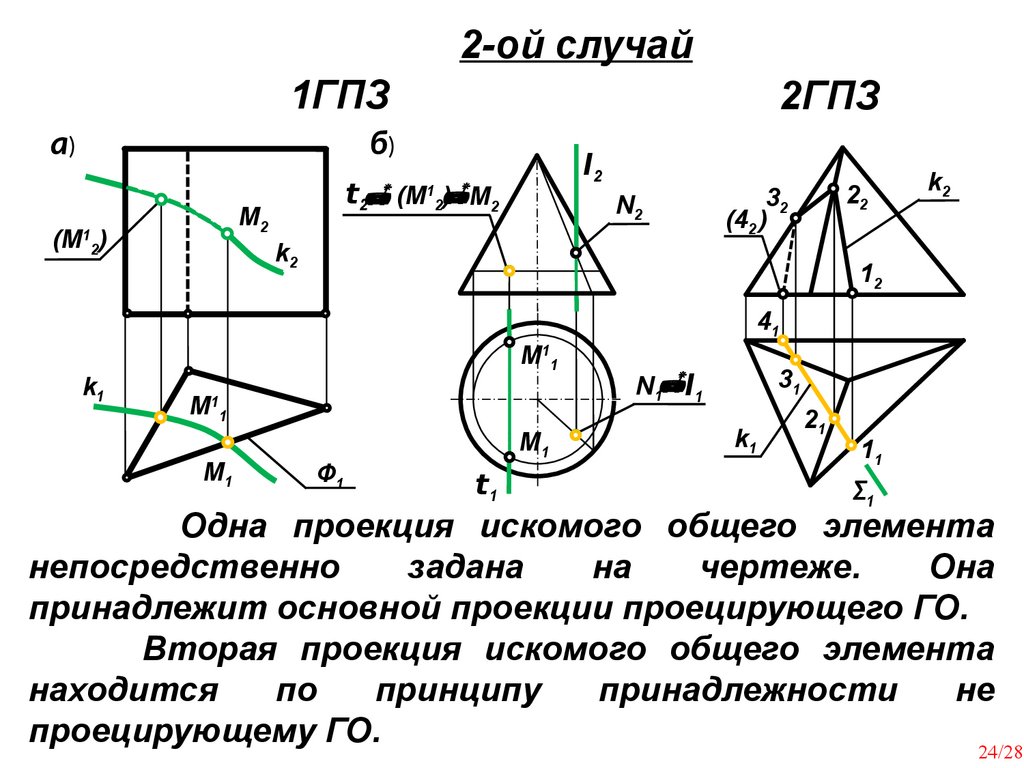
24.

1ГПЗ
а)
2-ой случай
б)
k1
t2 (M12
) M2
M2
(M12)
l2
N2
k2
1
1
M1
22
32
(42 )
k2
12
M1 1
M
2ГПЗ
Ф1
M1
t1
41
31
N1 l1
k1
21
11
Ʃ1
Одна проекция искомого общего элемента
непосредственно
задана
на
чертеже.
Она
принадлежит основной проекции проецирующего ГО.
Вторая проекция искомого общего элемента
находится
по
принципу
принадлежности
не
проецирующему ГО.
24/28

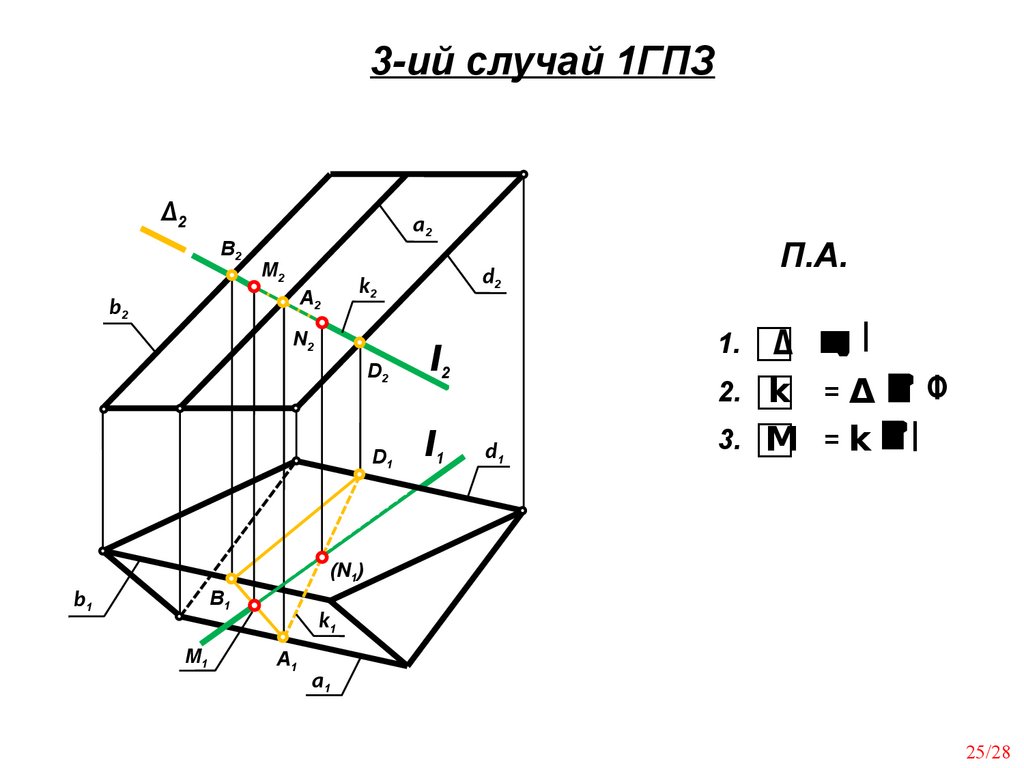
25.

3-ий случай 1ГПЗ
B2
a2
M2
k2
A2
b2
d2
N2
l2
D1
l1
d1
l
1.
Δ
2.
k
=Δ
D2
П.А.
∆2
3.
М =k
Ф
l
(N1)
b1
B1
M1
k1
A1
a1
25/28

26.

Алгоритм решения 3-его случая 1ГПЗ:
1. Заключаем прямую l в проецирующую плоскость ∆.
На чертеже проводим ∆2 через l2 .
2. Находим линию пересечения k проецирующей
плоскости ∆ с заданной поверхностью Ф. На
чертеже обозначаем k2 и по принадлежности
заданной поверхности находим k1 .
3.
Определяем искомые точки M и N получаемые
пересечении k и l . На чертеже k1 пересекается с l1 в
результате получаем горизонтальные проекции
точек M1 и
N1 , по линии проекционной связи
строим фронтальные проекции M2 и N2.
26/28

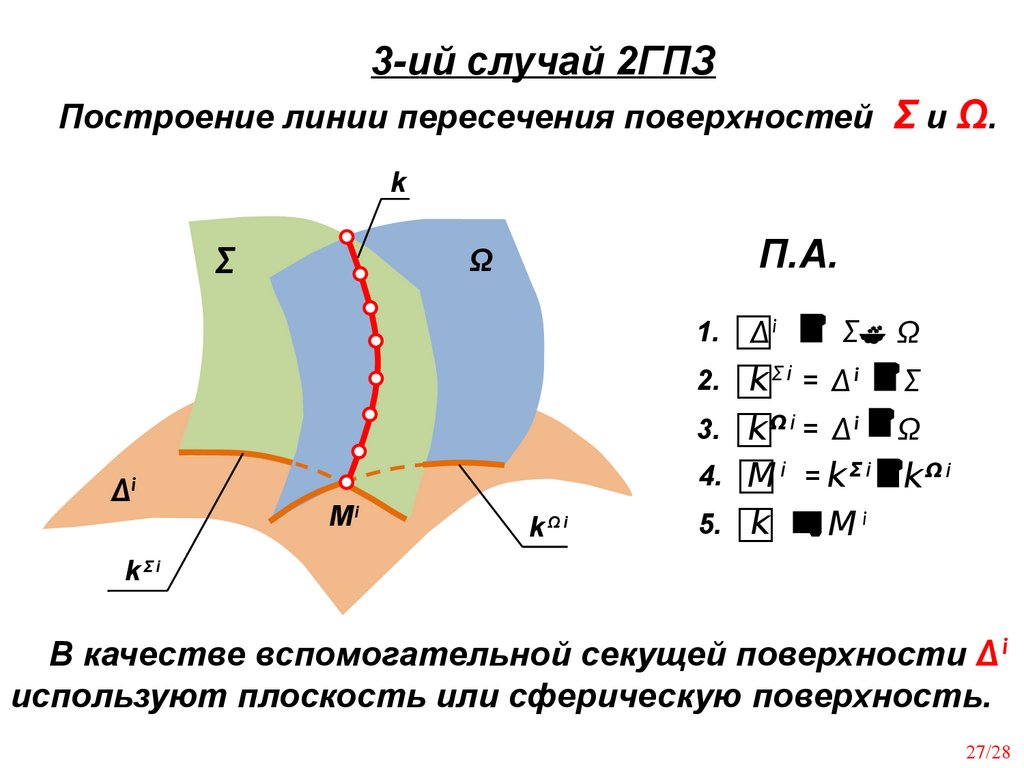
27.

3-ий случай 2ГПЗ
Построение линии пересечения поверхностей Σ и Ω.
k
П.А.
Ω
Ω
Σ
Ω
kΩi
Mi
kΩi
∆i
Σ
2.
kΣi = ∆i
3.
kΩi = ∆i
4.
Mi = kΣi
5.
k
Mi
1.
∆i
Σ
kΣi
В качестве вспомогательной секущей поверхности ∆ i
используют плоскость или сферическую поверхность.
27/28

28.

Алгоритм решения 3-его случая 2ГПЗ
1.
Проводим
вспомогательную
секущую
поверхность ∆ i , так чтобы она рассекала каждую из
заданных поверхностей по линиям, которые легко
построить (прямые, окружности).
2.
Находим линию k Ω i пересечения секущей
поверхности ∆ i с заданной поверхностью Ω .
3.
Находим линию k Σ i пересечения секущей
поверхности ∆ i с заданной поверхностью Σ .
4.
Линии k Ω i и k Σ i пересекаются, так как
принадлежат одной вспомогательной секущей
поверхности, в результате получим точку (точки),
общие для двух поверхностей.
5.
Линия пересечения k состоит из построенных
точек М i .
28/28

29.

Будь готов изменить свои цели, но никогда не
изменяй свои ценности.

30.

Конец лекции 4