Определение производной Лекция 11

1.

Определение производной
Производно й функции f в точке x0 называется число ,
к которому стремится разностное отношение
f ( x )
при x 0
x

2.

Нахождение производной по определению
1) f f ( x0 x) f ( x0 )
f f ( x0 x) f ( x0 )
2)
x
x
f
3) , при x 0
x

3.

«Если продолжить одно из
маленьких звеньев ломаной,
составляющей кривую линию,
то эта продолженная таким
образом сторона будет
называться касательной к
кривой.»

4.

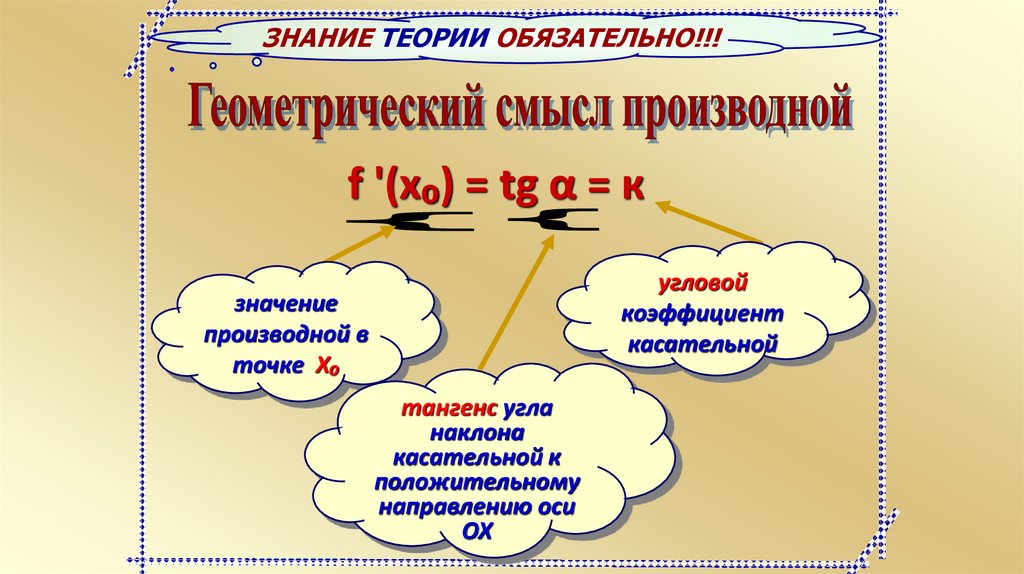
ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
f '(x₀) = tg α = к
угловой
коэффициент
касательной
значение
производной в
точке Х₀
тангенс угла
наклона
касательной к
положительному
направлению оси
ОХ

5.

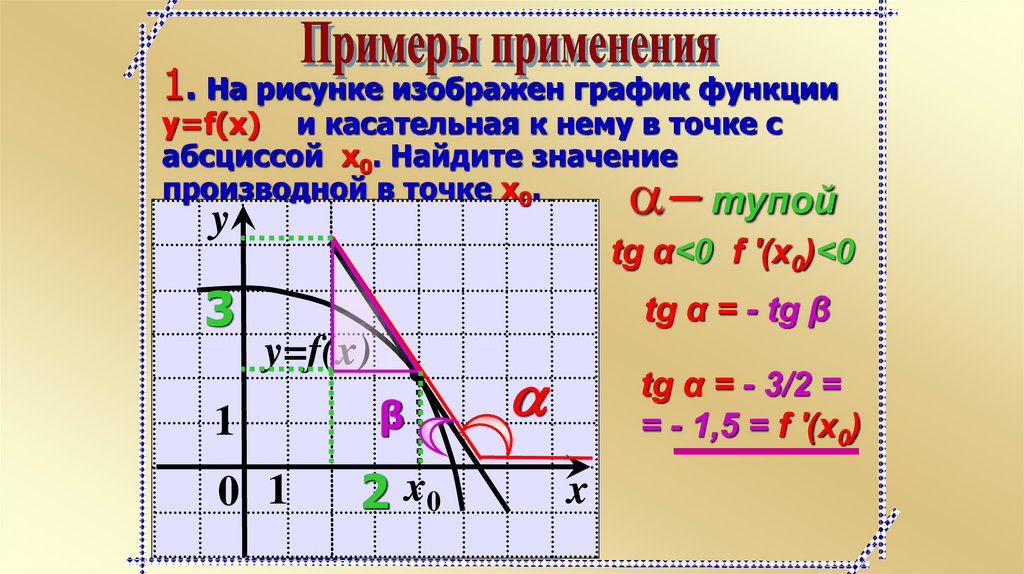
1. На рисунке изображен график функции
y=f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение
производной в точке x0.
тупой
a
y
tg α<0 f '(x0)<0
3
tg α = - tg β
y=f(x)
1
β
0 1
2 x0
a
tg α = - 3/2 =
= - 1,5 = f '(x0)
x

6.

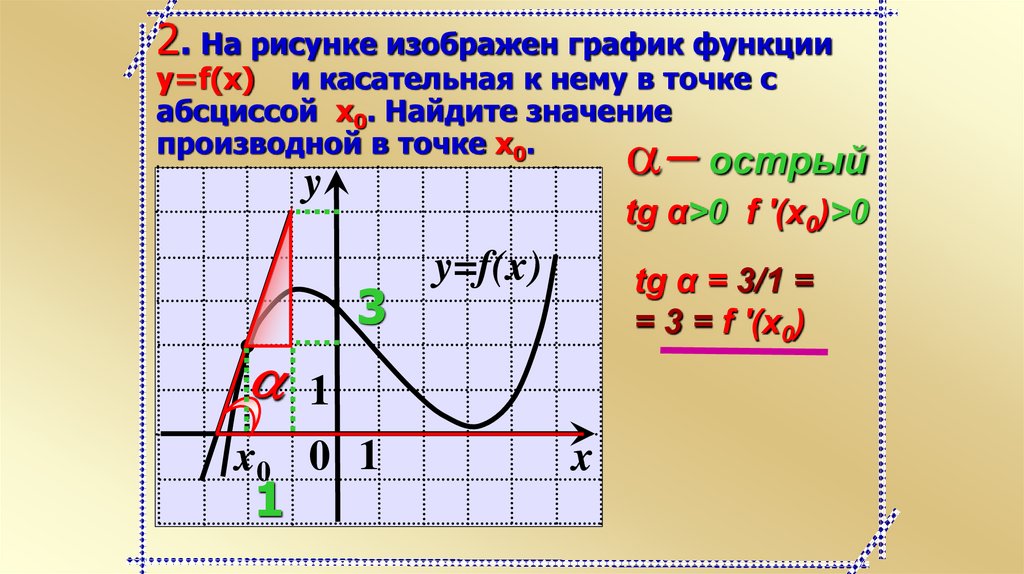
2. На рисунке изображен график функции
y=f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение
производной в точке x0.
a острый
y
tg α>0 f '(x0)>0
3
y=f(x)
tg α = 3/1 =
= 3 = f '(x0)
1
x0 0 1
1
x

7.

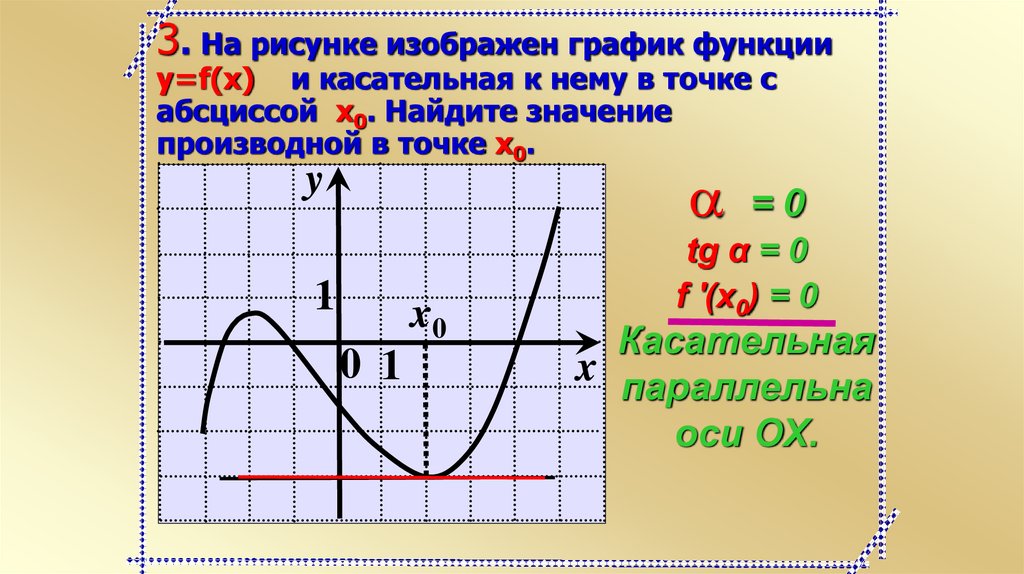
3. На рисунке изображен график функции
y=f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение
производной в точке x0.
a =0
y
1
x0
0 1
tg α = 0
f '(x0) = 0
Касательная
x параллельна
оси ОХ.

8.

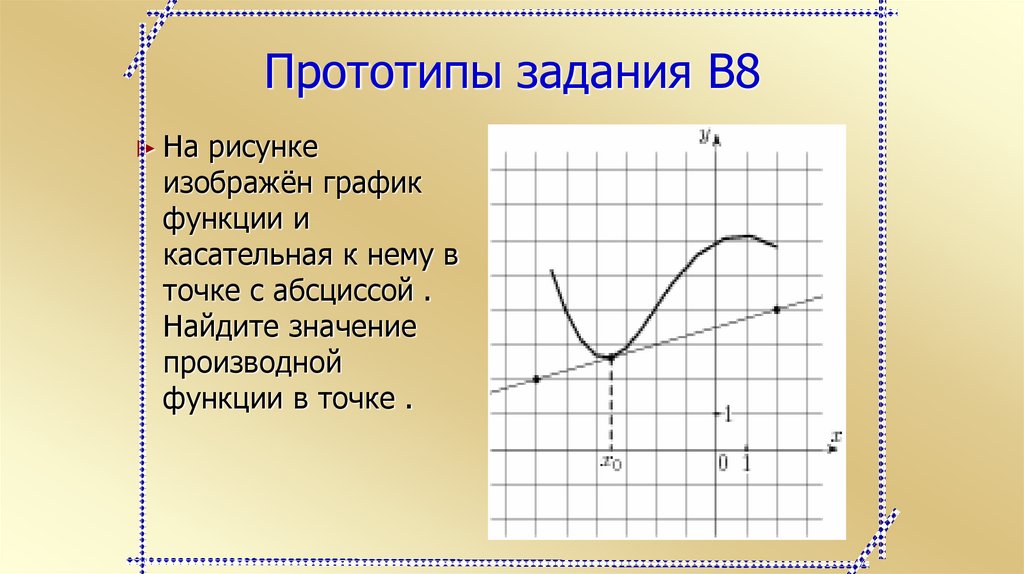
Прототипы задания B8
► На рисунке
изображён график
функции и
касательная к нему в
точке с абсциссой .
Найдите значение
производной
функции в точке .

9.

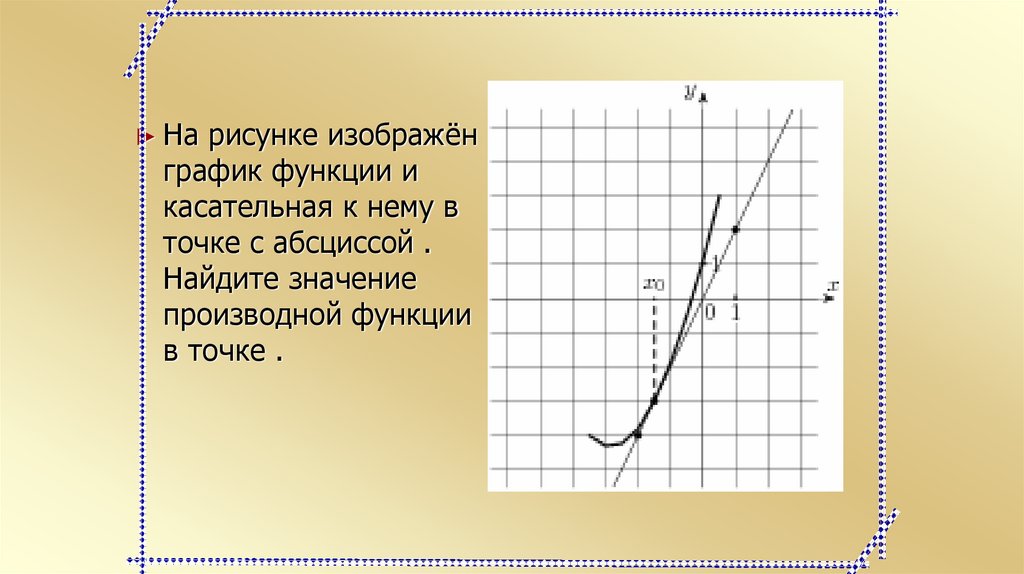
► На рисунке изображён
график функции и
касательная к нему в
точке с абсциссой .
Найдите значение
производной функции
в точке .

10.

► На рисунке изображён
график функции и
касательная к нему в
точке с абсциссой .
Найдите значение
производной функции
в точке .

11.

► На рисунке
изображён график
функции и
касательная к нему в
точке с абсциссой .
Найдите значение
производной
функции в точке .

12.

Производная функции y = f(x) в
точке x0 это скорость
изменения функции f (х) в точке
x0
x'(t) = (t)

13.

Применение производной
Производная нашла широкое применение:
а) в алгебре и началах анализа при исследовании функции и построении
графиков функций;
б) в физике при решении задач на нахождение скорости неравномерного
движения, плотности неоднородного тела и др.
в) в тригонометрии при вычислении тангенса угла наклона касательной к
кривой,
а также в геометрии, астрономии, аэродинамике, химии и экономике,
биологии и медицине.

14.

Задача по химии:
Пусть количество вещества,
вступившего в химическую реакцию
задается зависимостью:
р(t) = t2/2 + 3t –3 (моль)
Найти скорость химической реакции
через 3 секунды.

15.

Решение:
Понятие на
языке химии
Обозначение
Понятие на языке
математики
Количество в-ва
в момент
времени t0
p = p(t)
Функция
Интервал
времени
∆t = t2 – t1
Приращение аргумента
Изменение
количества в-ва
∆p = p(t+ t ) – p(t)
Приращение функции
∆p/∆t
Отношение приращён.
функции к приращён.
аргументу
Средняя
скорость
химической
реакции
V (t) = p ‘(t)