Математика-Лекция-1-часть-практики-1-1

1.

МАТЕМАТИКА
1 СЕМЕСТР
ЛЕКЦИЯ 1. МАТРИЦЫ. ДЕЙСТВИЯ С МАТРИЦАМИ.
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
СОПРОВОЖДАЮЩИЙ КУРС:
МАТЕМАТИКА ИТС (ПОТОРОЧИНА К.С.) (МАТЕМ1)

2. Литература

1. Краснов М.Л., Киселев А.И., Макаренко Г.И. Вся высшая
математика: Учебник. М, 2003. Т. 1.
2. Письменный Д.Т. Конспект лекций по высшей математике
/Д.Т.Письменный. Ч.1. М, 2006.
3. Берман Г.Н. Сборник задач и упражнений по
математическому анализу. Учебное пособие. СПб, 2006.
4.Клетеник Д. В. Сборник задач по аналитической геометрии.
СПб, 2002.
5. Сборник задач по математике для втузов. Ч.1., Ч.2
/ под ред. А.В. Ефимова и А.С. Поспелова. М, 2003.

3.

Основные обозначения
- для всех, для любого (всякий, любой);
- существует, найдется;
! – существует (найдется) единственный;
знак заменяет выражение «тогда и только тогда,
когда»;
знак заменяет выражение «следует», «следовательно»;
знак заменяет выражение «такой, что», «такое, что»

4.

Тема 1. Элементы линейной алгебры
2x 3y 5
5 x 7 y 12
x 2 y 3z 5
2x y z 1
x 3y 4z 7

5.

Тема 1. Элементы линейной алгебры
§1. Понятие матрицы. Действия с матрицами
Определение 1. матрицей размера m n будем понимать совокупность
m n чисел, расположенных в виде прямоугольной таблицы, содержащей
m строк и n столбцов. Обозначение:
a11 a12
a
a22
21
A
...
...
am1 am 2
... a1n
... a2 n
aij ,
... ...
... amn
aij элементы матрицы, первый индекс i обозначает номер строки,
второй индекс j обозначает номер столбца.

6.

Определение 2. Любая матрица, имеющая одинаковое число строк и столбцов
(m=n), называется квадратной матрицей порядка n.
Ее элементы a11, a22,…, ann составляют главную диагональ,
a1n, a2 (n-1),…, an1 − побочную диагональ.
При m=n=1 матрица состоит из одного числа и отождествляется с ним.

7.

Частные виды матриц:
- матрица-столбец (матрица размера m 1):
- матрица-строка (матрица размера 1 n):
a
a
- ступенчатая матрица: 11 12
0 a
22
... ...
0
0
где aii 0 (i=1,2,…,m; m<n);
a11
... a1m
... a2 m
... ...
... amm
a11
a
21 ;
...
a
m1
a12 ... a1n ;
a1m 1
a2 m 1
...
amm 1
... a1n
... a2 n
,
... ...
... amn

8.

- треугольная матрица – квадратная матрица, в которой все элементы выше
(ниже) главной диагонали равны нулю:
a11 a12
0 a
22
... ...
0
0
... a1n
... a2 n
;
... ...
... ann
- диагональная матрица – квадратная матрица, в которой отличны от нуля
только элементы главной диагонали:
a11 0
0 a
22
... ...
0
0
... 0
... 0
;
... ...
... ann

9.

- скалярная матрица – диагональная матрица, все элементы которой
равны (a11 = a22 = … = ann = λ):
0 ... 0
0 ... 0
;
... ... ... ...
0
0
...
- единичная матрица E – скалярная матрица при λ=1:
1 0 ... 0
0 1 ... 0
;
E
... ... ... ...
0
0
...
1
- нулевая матрица ϴ – матрица, все элементы которой равны нулю.

10.

Отношения на множестве матриц
Две матрицы A=(aij) и B=(bij) называются равными, если они одного
размера и соответствующие их элементы равны: aij=bij
(i = 1, 2, …, m; j = 1, 2, …, n).
Действия с матрицами
1. Сумма A+B матриц A и B одного размера m n есть матрица C того же
размера, где cij= aij+bij .
Свойства сложения:
- A+ϴ= ϴ +A=А;
- A+B=B+A;
- (A+B)+С= A+(B+С).

11.

2. Операция умножения матрицы на число состоит в умножении
каждого элемента матрицы на это число:
Свойства операции: A A ( aij ).
- ( ) A A A;
- ( A B) A B.
1 1 2
4 1 3
, B
.
Пример. Найти матрицу C=2A−4B, если A
0 3 1
2 0 2

12.

3. Операция умножения матрицы Am n на матрицу B k p определена только
в том случае, если число столбцов матрицы A равно числу строк матрицы
B, то есть n=k.
Определим первоначально умножение матрицы-строки
b11
b
A a11 a12 ... a1n на матрицу-столбец
B 21 :
...
n
bn1
A B a11 b11 a12 b21 ... a1n bn1 a1s bs1.
s 1
Тогда произведением матрицы A размера m n на матрицу B размером
n p называется матрица C=A B размера m p, элементы которой
получаются следующим образом: каждая i строка матрицы A
последовательно умножается на каждый j столбец матрицы B и
n
записывается в i–ю строку и j–й столбец матрицы C:
cij ais bsj .
s 1

13.

Пример. Вычислить A B и B A, если
4 2
1 2 4
1 5 .
A
,
B
2
3
0
8 6

14.

Свойства операции:
- A(B+C)=AB+AC;
- (A+B)C=AC+BC;
- A(λB)=λ(AB);
- (AB)C=A(BC);
- AE=EA=A.
Определение 3. Целой положительной степенью Ak (k>1) квадратной матрицы A
называется произведение k матриц, каждая из которых равна A.
Матрица Ak имеет тот же порядок, что и A, при этом A0=E.

15.

4. Транспонированием матрицы называется операция замены
строк матрицы ее столбцами с сохранением их номеров
(обозначение: АТ).
1 4
1 2 3
2 5 .
Т
Пример. Если A
то
A
,
4
5
6
3 6
Для матрицы-строки транспонированной будет матрица-столбец
и наоборот.
Определение 4. Матрица А называется симметричной, если
AT=A.

16.

Свойства операции:
- (A+B) T=AT+BT;
- (αA) T=αAT;
- (AT) T=A;
- (A B) T=BT AT.

17.

§ 2. Определители и их свойства
Квадратной матрице А порядка n можно сопоставить число detA
(|A|, ∆), которое называется определителем (детерминантом)
матрицы А.
Если n=1, А=(a11), то detA= a11.
Если n=2,
a11
A
a21
a12
a11
, то det A=
a22
a21
Если n=3,
a11
A a21
a
31
a12
a22
a32
a12
a11a22 a12 a21.
a22
a13
a23 , то
a33
det A=a11a22 a33 a12 a23a31 a13a21a32 a13a22 a31 a12 a21a33 a11a23a32 .

18.

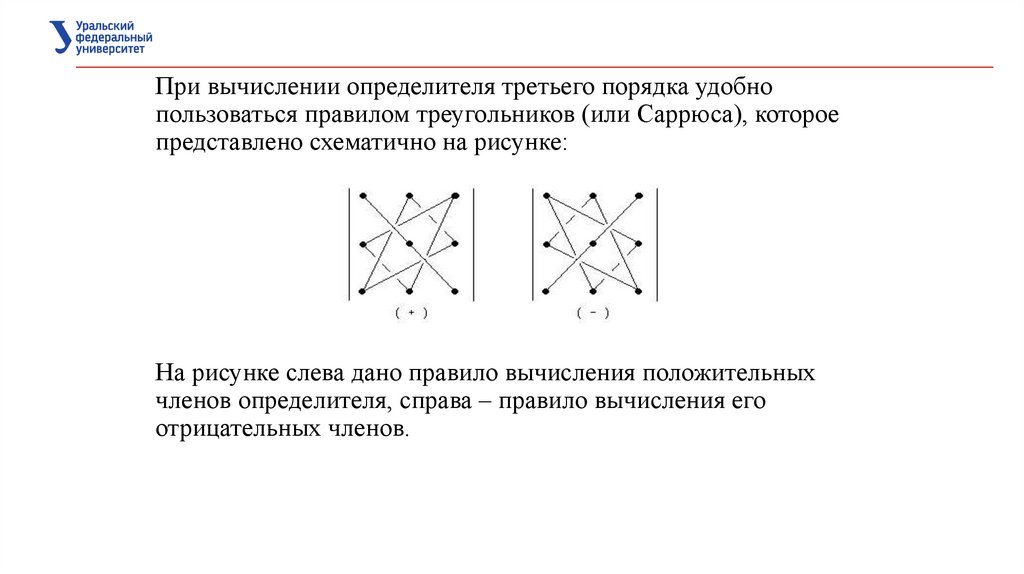
При вычислении определителя третьего порядка удобно
пользоваться правилом треугольников (или Саррюса), которое
представлено схематично на рисунке:
На рисунке слева дано правило вычисления положительных
членов определителя, справа – правило вычисления его
отрицательных членов.

19.

1 2 3
Пример. Вычислить 4 5 6 .
7 8 9

20.

СТРОГОЕ ОПРЕДЕЛЕНИЕ
Понятие определителя n-го порядка связано с понятием перестановки.
Перестановками из n элементов называют комбинации, состоящие из одних и тех
же п различных элементов и отличающиеся только порядком их расположения.
Пусть дано n натуральных чисел.
(1, 2,…, n) – естественная перестановка;
(α1, α2,…, αn) – произвольная перестановка.
Число всех возможных перестановок из n чисел равно n!.
Два числа в перестановке образуют инверсию, если большее число стоит впереди
меньшего.

21.

Например, в перестановке (3, 1, 2) инверсию образуют пары
(3, 1) и (3, 2).
В перестановке (1, 4, 3, 2) инверсии образуют следующие пары:
(4, 3), (4, 2), (3, 2).
Число инверсий в перестановке (α1, α2,…, αn) будем обозначать через J.
J(α1, α2,…, αn) = J1+J2+…+Jn-1, где Ji (i = 1, 2,…, n 1) число чисел, стоящих перед
числом i в перестановке, больших числа i (если таковые имеются).
J(1, 4, 3, 2)= J1+J2+J3=0+2+1=3. Итак, J(1, 4, 3, 2)=3.
Перестановка называется четной, если суммарное количество инверсий в
перестановке – четное число и нечетной, если нечетное число.

22.

Пусть дана матрица Аn n.
Определителем порядка n называется число, полученное из элементов
данной матрицы по следующему правилу:
а) это алгебраическая сумма n! слагаемых;
б) каждое слагаемое определителя является произведением n элементов
матрицы А, взятых по одному из каждой строки и каждого столбца;
в) каждому члену определителя приписывается знак «+», если эта
перестановка четная, при условии, что первые индексы элементов
произведения расположены в естественном порядке и знак « », если нечетная.
J 1 , 2 , , n
det
A
1
a1 1 a2 2 an n .
Итак, по определению
n!

23.

Это определение распространяется и на определители второго и третьего
порядков.
Например,
a11
A
a21
a12
a11a22 a12 a21.
a22

24.

Определение 5. Минором Mij элемента aij матрицы A порядка n называется
определитель матрицы (n 1)-го порядка, полученной из данной вычеркиванием i-ой
строки и j-го столбца.
Определение 6. Алгебраическим дополнением элемента aij матрицы A называют
число
Аij = ( 1)i+j Mij.
a11
Пример 1. Для матрицы A
a21
a12
найти все алгебраические дополнения.
a22

25.

26.

Свойства определителей
1. Определитель не меняется при транспонировании матрицы:
det A = det AT.
2. При перестановке местами двух строк (столбцов) определитель меняет знак на
противоположный.
3. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
4. Общий множитель строки (столбца) можно вынести за знак определителя.
5. Определитель, содержащий нулевую строку (столбец), равен нулю.
6. Определитель не изменится, если к некоторой строке (столбцу) прибавить другую
строку (столбец), умноженную на число 0.

27.

7. Если все элементы i-ой строки (столбца) определителя представлены в виде суммы
двух слагаемых aij=bij+cij, то определитель равен сумме двух определителей, у которых
все строки (столбцы), кроме i-ой, такие же, как и в заданном определителе, а i-ая
строка в одном из слагаемых состоит из элементов bij, в другом – из cij.
8. (Теорема разложения.) Определитель матрицы равен сумме произведений
элементов любой строки (любого столбца) матрицы A на их алгебраические
дополнения, т.е.
9. (Теорема аннулирования.) Сумма произведений элементов одной строки (столбца)
матрицы A на алгебраические дополнения элементов другой строки (столбца) равна
нулю.
10. det(A B) = detA detB.

28.

Основные способы вычисления определителей n-го порядка
1) по определению (например, вычисление определителей второго и третьего
порядков);
2) по формуле разложения (свойство 8);
3) приведение определителя к треугольному виду, используя свойства (2, 4, 6):
det A det A
a12
a1 n
a11
a2 n
0 a22
0
0
ann
a22
ann
.
a11

29.

Пример 2. Вычислить 3 1
2 1
0 1
3 1
2 3 используя свойства определителей.
1 0
,
2 1
6 1