Похожие презентации:
Матрицы. Действия с матрицами
1. МАТРИЦЫ. ДЕЙСТВИЯ С МАТРИЦАМИ.
2. Основные определения
Определение. Матрицейразмера m n, где m- число
строк, n- число столбцов,
называется таблица чисел,
расположенных в
определенном порядке. Эти
числа называются
элементами матрицы.
Элементы матрицы
обозначаются aij, где i- номер
строки, а j- номер столбца.
a11 a12
a21 a22
... ...
a
m1 am 2
... a1n
... a2 n
... ...
... amn
3.
Матрица может состоять как из однойстроки, так и из одного столбца. Вообще
говоря, матрица может состоять даже
из одного элемента
Определение. Если число столбцов
матрицы равно числу строк (m=n), то
матрица называется квадратной
4.
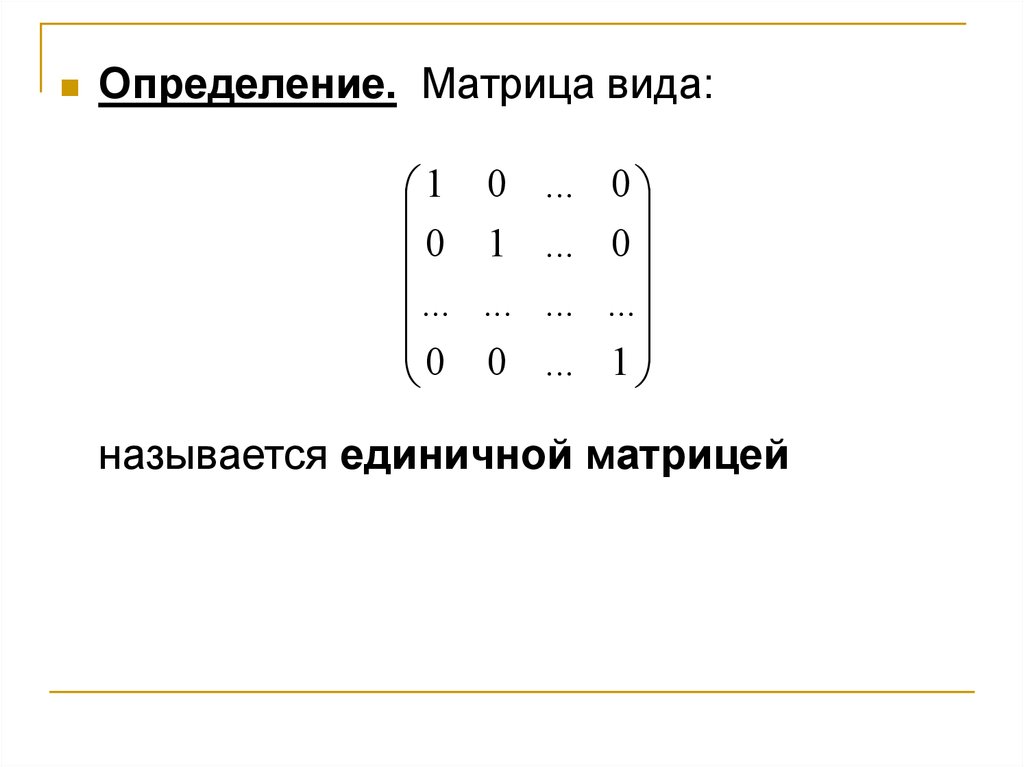
Определение. Матрица вида:1
0
...
0
0 ... 0
1 ... 0
... ... ...
0 ... 1
называется единичной матрицей
5.
Определение. Если amn = anm , то матрицаназывается симметрической
Определение. Квадратная матрица вида
называется диагональной матрицей
a11
0
...
0
0
a 22
...
0
0
... 0
... 0
... a nn
...
6. Основные действия над матрицами
Сложение и вычитание матриц сводитсяк соответствующим операциям над их
элементами. Самым главным свойством
этих операций является то, что они
определены только для матриц
одинакового размера.
7.
Определение. Суммой (разностью)матриц является матрица, элементами
которой являются соответственно
сумма (разность) элементов исходных
матриц.
cij = aij bij
С = А + В = В + А.
8.
Операция умножения (деления)матрицы любого размера на произвольное
число сводится к умножению (делению)
каждого элемента матрицы на это число.
(А+В) = А В
А( ) = А А
a11
a 21
A
...
a
m1
a12
a 22
...
a m 2
... a1n
... a 2 n
...
...
... a mn
9. Операция умножения матриц
Определение: Произведением матрицназывается матрица, элементы которой
могут быть вычислены по следующим
формулам:
Из приведенного определения
A B = C;
видно, что операция
умножения матриц
n
определена только для
сij aik bkj матриц, число столбцов
k 1
первой из которых равно
числу строк второй.
10.
1121
12
22
...
...
...
...
...
...
...
...
...
...
1l
2l
...
...
...
...
...
...
...
j1
j2
...
...
...
...
...
...
...
...
...
...
...
...
m1 m 2
11
21
12
22
...
1i
2i
...
...
...
j1
j2
...
...
m1 m 2
...
1i
2i
...
...
1n
2n
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
jl
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
ml
...
...
...
...
...
...
l1
l 2
...
li
...
ln
...
1n
2n
...
...
...
...
ji
...
jn
...
...
...
...
...
mi
...
mn
...
11 12
21 22
...
l
ji jk ki
k 1
11. Свойства операции умножения матриц
1)Умножение матриц не коммутативно,т.е. АВ ВА даже если определены оба
произведения. Однако, если для каких – либо
матриц соотношение АВ=ВА выполняется, то такие
матрицы называются перестановочными.
Перестановочными могут быть только квадратные
матрицы одного и того же порядка.
Заметим: А Е = Е А = А
Очевидно, что для любых матриц выполняются
следующее свойство:
A O = O; O A = O, где О – нулевая матрица.
12.
2) Операция перемножения матрицассоциативна, т.е. если определены
произведения АВ и (АВ)С, то определены
ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц
дистрибутивна по отношению к
сложению, т.е. если имеют смысл
выражения А(В+С) и (А+В)С, то
соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
13.
4) Если произведение АВ определено, то длялюбого числа верно соотношение:
(AB) = ( A)B = A( B).
5) Если определено произведение АВ , то
определено произведение ВТАТ и
выполняется равенство:
(АВ)Т = ВТАТ, где индексом Т обозначается
транспонированная матрица.
6) Заметим также, что для любых квадратных
матриц det (AB) = detA detB.
(Понятие det (определитель, детерминант) будет
рассмотрено ниже).
14. Операция транспонирования
Транспонированием матрицы называетсяоперация, в результате которой образуется новая
матрица, где строками служат столбцы исходной,
записанные с сохранением порядка их следования
* *
1
* *
* *
2
* *
* * * * * *
*
*
* *
3
* *
* * * * * *
*
*
* *
...
* *
* *
k
*транспонирование
*
1 2 3 ... k ... n 1 n
* *
...
* *
* * n 1 * *
* *
n
* *
* * * * * *
*
*
* * * * * *
*
*
15.
Для элементов транспонированнойT
матрицы A
при верно равенство:
j i
T
ij
i [1, m] , j [1, n]
Операция транспонирования не изменяет
симметрическую матрицу, но переводит
строку размера 1xm в столбец размера
mx1 и наоборот.
.
16. Элементарные преобразования матрицы
Определение. Элементарнымипреобразованиями матрицы назовем
следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки
элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из
одинаковых строк (столбцов);
5) транспонирование.
17.
Те же операции, применяемые длястолбцов, также называются
элементарными преобразованиями.
С помощью элементарных
преобразований можно к какой-либо
строке или столбцу прибавить линейную
комбинацию остальных строк ( столбцов ).
18. Обратная матрица
Определение. Если существуютквадратные матрицы Х и А одного
порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого
порядка, что и матрица А, то матрица Х
называется обратной к матрице А и
обозначается А-1.
19. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ (1 способ)
20.
К матрице Aij «дописывают» справаединичную матрицу. С помощью
элементарных преобразований приводят
матрицу Aij к единичному виду, тогда матица,
которая получится справа – обратная
a11
an1
a12
an 2
0 ... 0
...
...
...
...
...
...
... ann 0 0 ... 1
a1n 1
21. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ
обратная матрица позволяет найтирешения следующих матричных
уравнений:
АХ=С
ХВ=С
АХВ=С
Решение:
Х=А-1С
Х=СВ-1
Х=А-1СВ-1
22. Замечание:
В качестве всех или некоторых элементовматрицы возможно использование не
только чисел, но и других математических
объектов, для которых подходящим
образом определены операции сравнения,
сложения и умножения на число,
например, векторов, функций или тех же
матриц.





















 Математика
Математика