Похожие презентации:
Определитель и метод Крамера
1. ТЕМА № 2
«ОПРЕДЕЛИТЕЛИИ ИХ ПРИМЕНЕНИЯ»
1
2. ОБОЗНАЧЕНИЯ
КВАДРАТНАЯ МАТРИЦА n-го ПОРЯДКАa11
A
a
n1
a1n
ann
ОБОЗНАЧЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
a11
a1n
an1
ann
A det A
2
3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1-го ПОРЯДКАa11 a11
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2-го ПОРЯДКА
a11
a12
a21 a22
a11 a22 a21 a12
3
4. Вычисление определителя матрицы 3-го порядка
Правило Саррюса4
5. Пример
6. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
67. ОБЩИЙ ВИД СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ
a11 x1 a12 x2 a1n xn b1 ,a x a x a x b ,
21 1 22 2
2n n
2
an1 x1 aт 2 x2 ann xn bn
7
8. Пример
2 x y 3z 13,4 x 3 y z 7,
x 2 y 5 z 15
2 x1 x2 3x3 13
4 x1 3x2 x3 7
x 2 x 5 x 15
2
3
1
8
9. НЕОБХОДИМОЕ УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛ КРАМЕРА
a11a12
a21 a22
a31
a32
a13
a23 0
a33
9
10. ВЫЧИСЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ
b1a12
a13
a11
b1
a13
1 b2
a22
a23 ;
2 a21 b2
a23
b3
a32
a33
a31
a33
a11
a12
b1
3 a21 a22
b2
a31
b3
a32
b3
10
11. ФОРМУЛЫ КРАМЕРА ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
1x1 ,
2
x2
,
3
x3
11
12. РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ
2 x y 3z 13,4 x 3 y z 7,
x 2 y 5 z 15
12
13. ВЫЧИСЛЕНИЕ ГЛАВНОГО И ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ
24
1
1
3
3 1 30 24 1 9 4 20 14 0,
2
5
13
14.
13 11 7
3
15 2
3
1 195 42 15 135 26 35 42,
5
14
15.
2 132 4
7
1 15
3
1 70 130 13 21 30 260 14,
5
15
16.
2 1 133 4
3
7 90 140 7 39 28 60 28.
1 2 15
16
17. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ
1 42x
3,
14
2 14
y
1,
14
3 28
z
2.
14
17
18.
2 x y 3z 13,4 x 3 y z 7,
x 2 y 5 z 15
18













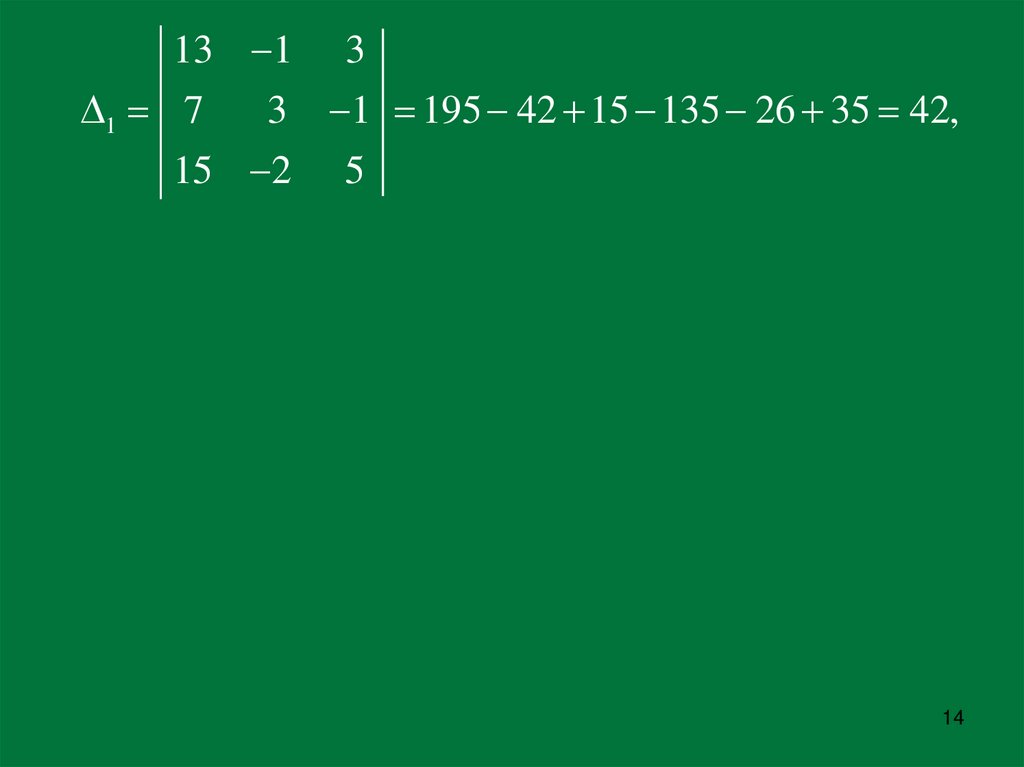
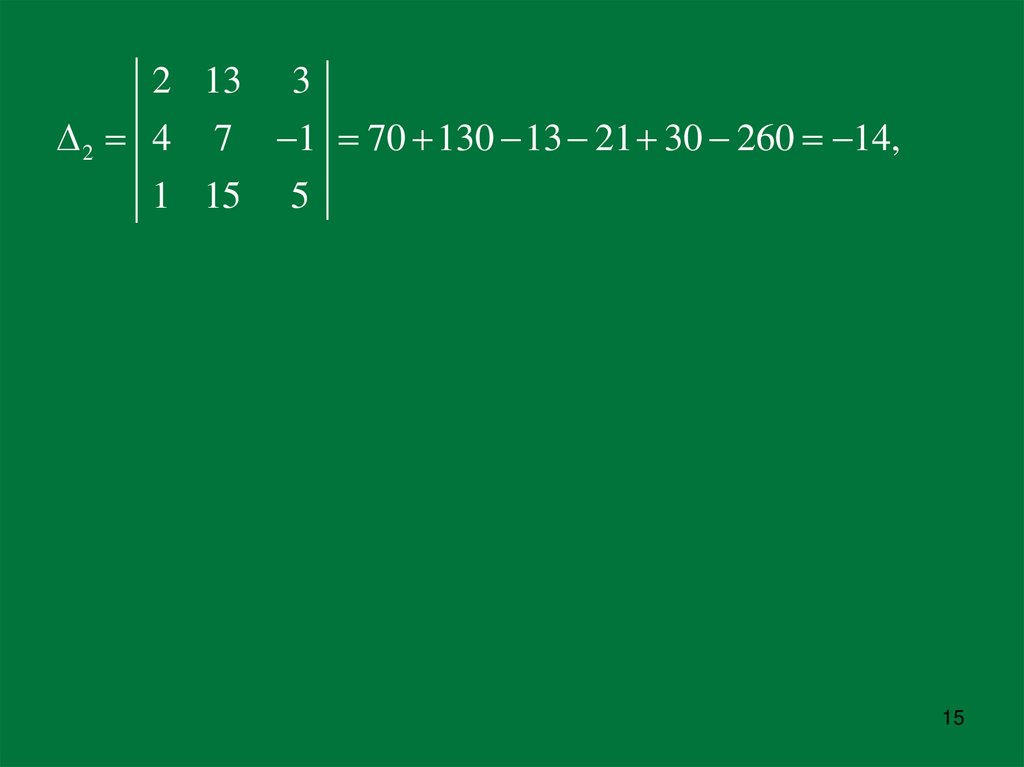



 Математика
Математика








