Доверительные интервалы для оценки математического ожидания a нормального распределения при неизвестном

1.

§ 9. Доверительные интервалы для оценки математического
ожидания a нормального распределения при неизвестном
Пусть количественный признак X генеральной совокупности
распределен нормально с неизвестными параметрами a и . Необходимо
оценить математическое ожидание a с помощью выборочной средней xв
и доверительных интервалов при заданной надежности .
Введем безразмерную случайную величину
x a
,
T в
S n
где xв – выборочное среднее,
a – неизвестное математическое ожидание нормального
распределения,
S – исправленное выборочное среднее квадратическое отклонение
1 n
2
,
S
x
x
i
в
n 1 i 1
n – объем выборки.

2.

Случайная величина T имеет распределение Стьюдента с k n 1
степенями свободы, которое определяется только объемом выборки n и
не зависит от неизвестных параметров a и .
Пусть выполняется условие:
xв a
P
t .
S n
Отсюда получим
t S
t S
.
P xв
a xв
n
n
Из этого условия по таблицам значений t t , n по заданным
величинам и n находим t и определяем доверительный интервал
xв
t S
n
a xв
t S
n
.

3.

Пример. Количественный признак X генеральной совокупности
распределен нормально. По выборке объема n 9 найдены выборочное
среднее xв 19,1 и исправленное среднее квадратическое отклонение
S 3 . Оценить неизвестное математическое ожидание при помощи
доверительного интервала с надежностью 0,99 .
Решение. По таблице значений t по заданным величинам 0,99 и
n 9 находим t 3,36 . Находим доверительные границы:
t S
3,36 3
3,36 3
x
19,1
15,64 , x
19,1
22,46 .
3
3
n
n
Следовательно, выполняется неравенство
15,64 a 22,46
с вероятностью 0,99 .
t S

4.

§ 10. Оценка истинного значения измеряемой величины
Пусть производится n независимых равноточных измерений
физической величины, истинное значение a которой неизвестно. Будем
рассматривать результаты отдельных измерений x1 , x2 , ..., xn как
случайные величины X 1 , X 2 , ..., X n . Эти величины независимы (так как
измерения независимы), имеют одно и то же математическое ожидание a
(равное истинному значению измеряемой величины), одинаковые
дисперсии 2 (так как измерения равноточные), распределены
нормально (это подтверждается опытом). Так как выполняются все
условия для определения доверительных интервалов, то можно
использовать ранее полученные формулы для оценки математического
ожидания.
Пример. По данным n 16 независимых равноточных измерений
физической величины определены среднее арифметическое результатов
отдельных измерений xв 22,22 и исправленное среднее квадратическое
отклонение S 4,0 . Необходимо оценить истинное значение измеряемой
величины с надежностью 0,99 .

5.

Решение. Истинное значение измеряемой величины равно ее
математическому ожиданию. Поэтому задача сводится к оценке
математического ожидания при неизвестном при помощи
доверительного интервала
t S
t S
x
a x
.
n
n
По таблице значений t при 0,99 и n 16 находим t 2,95 .
Точность оценки равна
t S 2,95 4
2,95 .
4
n
Доверительные границы равны
t S
t S
x
22,22 2,95 19,27 , x
22,22 2,95 25,17 .
n
n
Следовательно, с надежностью 0,99 истинное значение измеряемой
величины заключено в доверительном интервале 19,27; 25,17 .

6.

§ 10. Условные средние. Корреляционная
Регрессия. Две основные задачи теории корреляции
зависимость.
Функциональной называют зависимость между двумя случайными
величинами, когда каждому возможному значению одной случайной
величины соответствует только одно возможное значение другой.
Статистической называют зависимость между двумя случайными
величинами, когда каждому возможному значению одной случайной
величины соответствует множество возможных значений другой.
Корреляционной называют зависимость между двумя случайными
величинами, когда каждому значению одной случайной величины
соответствует условное среднее значение другой.
Условным средним y x называют среднее арифметическое
наблюдавшихся значений случайной величины Y, соответствующих
значению случайной величины X x .

7.

Пример.
При
x1 15
величина
приняла значения
3 4 5
y1 3, y 2 4, y 3 5 . Условное среднее равно y x1
4.
3
Условным средним x y называют среднее арифметическое
Y
наблюдавшихся значений X, соответствующих Y y .
Пример. При y1 5 величина X приняла значения x1 13, x2 14,
13 14 15
x3 15 . Условное среднее равно x y1
14 .
3
Корреляционной зависимостью Y от X называют функциональную
зависимость условной средней y x от x:
y x f x .
Это уравнение называют уравнением регрессии Y на X; функцию f x
называют регрессией Y на X, график функции y x f x называют линией
регрессии Y на X.

8.

Корреляционной зависимостью X от Y называют функциональную
зависимость условной средней x y от y:
x y y .
Это уравнение называют уравнением регрессии X на Y; функцию y
называют регрессией X на Y, график функции x y y называют линией
регрессии X на Y.
Первая задача теории корреляции – установить форму
корреляционной связи – вид функции регрессии (линейная, квадратичная
и т.д.). Если обе функции регрессии f x и y линейны, то
корреляцию называют линейной, в противном случае – нелинейной.
Вторая задача теории корреляции – оценить тесноту (силу)
корреляционной связи. Например, сила корреляционной зависимости Y
от X оценивается по величине рассеяния значений Y вокруг y x . Большое
рассеяние свидетельствует о слабой зависимости Y от X, либо об
отсутствии такой зависимости. Малое рассеяние указывает на наличие
сильной связи между Y и X, возможно функциональной.

9.

§ 11. Определение параметров выборочного уравнения прямой
линии регрессии по не сгруппированным данным
Пусть количественные признаки X и Y связаны линейной
корреляционной зависимостью. В этом случае линии регрессии Y на X и
линия регрессии X на Y будут прямыми линиями.
Пусть для отыскания уравнений этих прямых линий проведено n
независимых испытаний, в результате которых получено n пар чисел
x1 , y1 , x2 , y2 , ..., xn , yn .
Наблюдаемые пары чисел можно рассматривать как случайную
выборку из генеральной совокупности всех возможных значений
случайной величины X , Y . Поэтому величины и уравнения, найденные
по этим данным, называют выборочными.

10.

Пусть выборочное уравнение прямой линии регрессии Y на X имеет
вид
y x kx b ,
различные значения x признака X и соответствующие им значения y
признака Y наблюдались по одному разу. В этом случае использовать
понятие условной средней нет необходимости и искомое уравнение
регрессии можно просто записать так
y kx b .
Параметр k называют выборочным коэффициентом регрессии Y на X и
обозначают yx . Поэтому можно написать
y yx x b .
параметры
yx
Найдем
такие
и
b,
чтобы
точки
x1 , y1 , x2 , y2 , ..., xn , yn , построенные по данным наблюдений на
плоскости XOY, как можно ближе лежали к прямой Y yx x b .

11.

Отклонением (ошибкой) называют разность
i y i yx xi b , i 1,2,..., n ,
где yi – наблюдаемая ордината, соответствующая xi.
Согласно методу наименьших квадратов неизвестные параметры
находят из условия, чтобы сумма квадратов отклонений
n
Q i2
i 1
была минимальной. Это условие выполняется в случае, когда равны
нулю частные производные Q по yx и b:
Q
Q
0,
0.
yx
b
Применяя этот метод для нахождения параметров yx и b прямой линии
регрессии, получим
n
Q
2 yi yx xi b xi 0,
yx
i 1
n
Q 2 y x b 0,
i yx i
b
i 1

12.

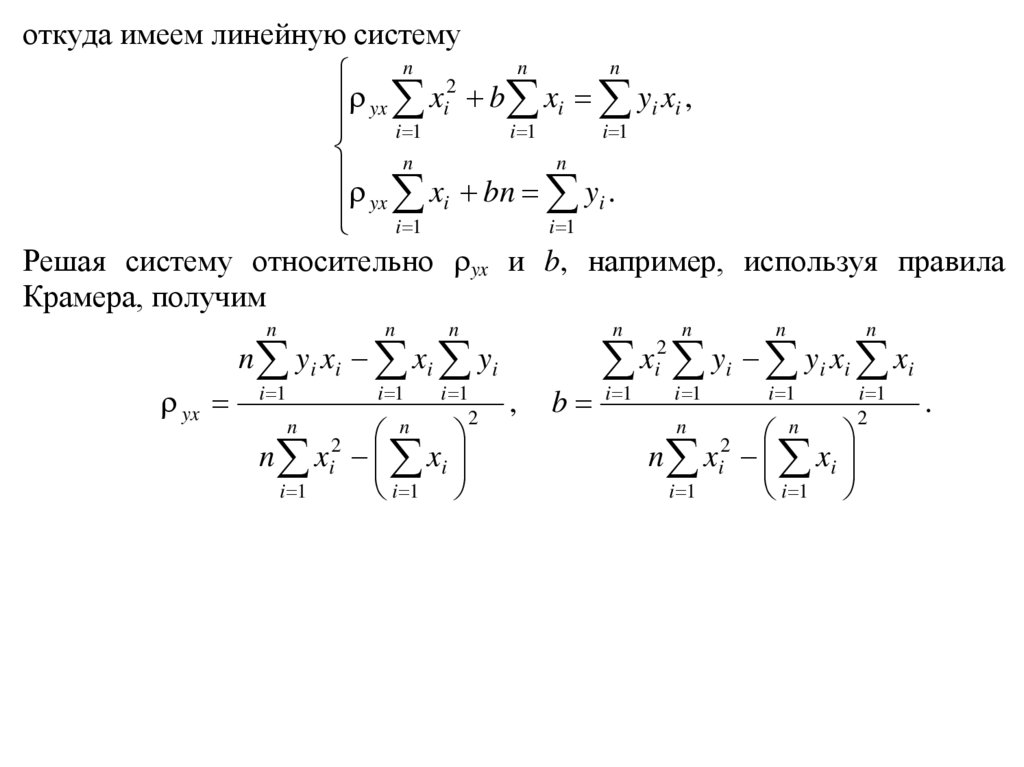
откуда имеем линейную систему
n
n
n
2
yx xi b xi yi xi ,
i 1
i 1
i 1
n
n
xi bn yi .
yx
i 1
i 1
Решая систему относительно yx и b, например, используя правила
Крамера, получим
n
yx
n
n
n
n y i xi x i y i
i 1
i 1
n
n
i 1
xi2
i 1
2
x
i
i 1
n
n
n
n
i 1
i 1
i 1
2
y i y i xi x i
,
b i 1
xi2
n
n
i 1
xi2
x
i
i 1
n
.