Фракталы: мир бесконечного разнообразия

1.

Фракталы: Мир
бесконечного разнообразия
Фракталы – это удивительные геометрические фигуры, которые
встречаются как в природе, так и в математике.
by Андрей Дубровский

2.

Что такое фрактал?
Определение
Бесконечная детальность
Фрактал – это геометрическая фигура, обладающая
Фракталы обладают бесконечной детальностью, при
свойством самоподобия, то есть её части подобны
увеличении масштаба обнаруживаются новые детали,
целой фигуре.
подобные исходной фигуре.

3.

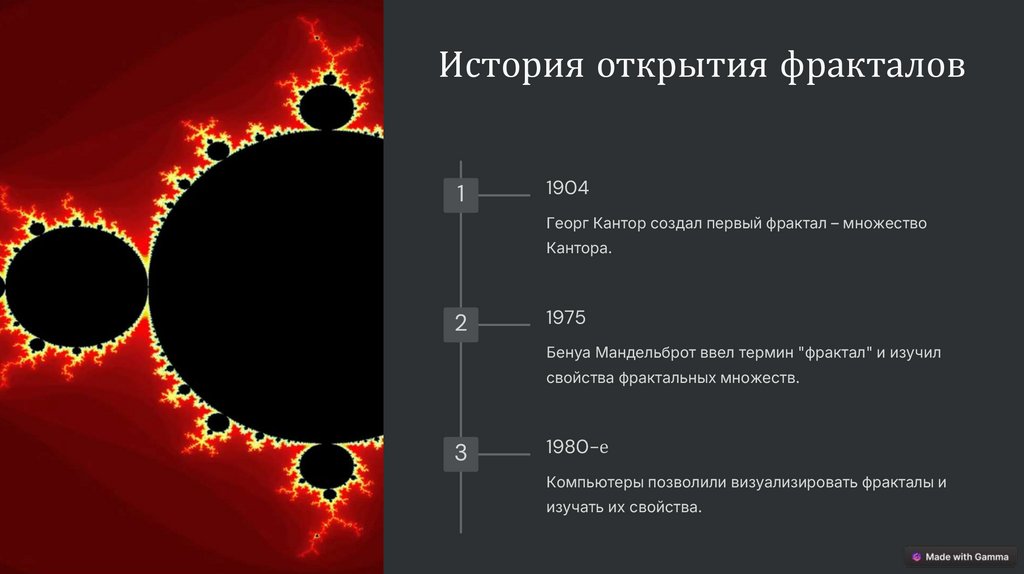
История открытия фракталов
1
1904
Георг Кантор создал первый фрактал – множество
Кантора.
2
1975
Бенуа Мандельброт ввел термин "фрактал" и изучил
свойства фрактальных множеств.
3
1980-е
Компьютеры позволили визуализировать фракталы и
изучать их свойства.

4.

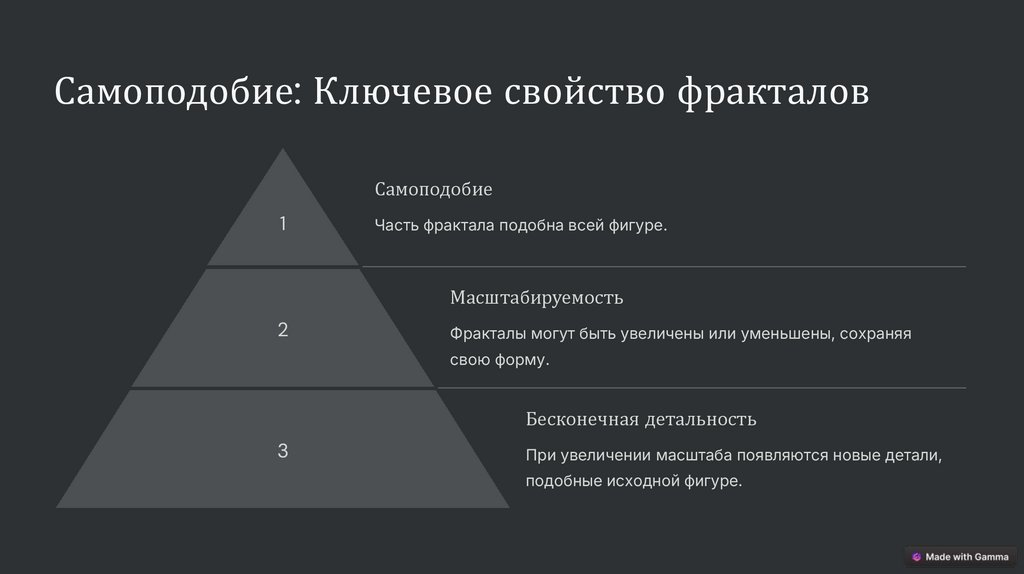
Самоподобие: Ключевое свойство фракталов
Самоподобие
1
Часть фрактала подобна всей фигуре.
Масштабируемость
2
Фракталы могут быть увеличены или уменьшены, сохраняя
свою форму.
Бесконечная детальность
3
При увеличении масштаба появляются новые детали,
подобные исходной фигуре.

5.

Примеры фракталов в
природе
Растения
Погода
Листья папоротника, ветви
Облака, молния, снежинки.
деревьев, кора некоторых
растений.
Животные
География
Раковина наутилуса,
Речные системы, береговые
кровеносная система.
линии.

6.

Применение фракталов в искусстве
Живопись
Архитектура
Музыка
Фрактальные узоры используются
Фрактальные формы придают
Фрактальные алгоритмы
для создания сложных и красивых
зданиям необычную эстетику и
используются для создания музыки
изображений.
функциональность.
с повторяющимися паттернами.

7.

Фрактальная геометрия
Евклидова геометрия
Изучает объекты с
Фрактальная
геометрия
гладкими кривыми и
Изучает объекты с
прямыми линиями.
самоподобием и
бесконечной
детальностью.
Применение
Моделирование природных объектов, создание новых
материалов.

8.

Алгоритмы построения
фракталов
Итерационные алгоритмы
Рекурсивные алгоритмы
Повторяющиеся действия,
Функции, которые вызывают сами
которые создают фрактал.
себя, создавая фрактал.
Программирование
Фракталы легко
программируются, что позволяет
создавать сложные формы.

9.

Фрактальная размерность
1.58
1.26
Множество Кантора
Кривая Коха
Фрактал с размерностью
Фрактал с размерностью
меньше 1.
больше 1, но меньше 2.
2.08
Множество Мандельброта
Фрактал с размерностью
больше 2, но меньше 3.

10.

Красота и сложность
фрактальных структур
Фракталы – это невероятные примеры красоты и сложности,
которые встречаются в природе и математике.