Тригонометрические функции y=sinx, y=cosx, y=tgx и y=ctgx, их графики и свойства. Сжатие и растяжение тригонометрических функций

1.

Математика
Государственное автономное профессиональное
образовательное учреждение
«Липецкий медицинский колледж»
Тригонометрические функции
y=sinx, y=cosx, y=tgx и y=ctgx, их графики и
свойства.
Сжатие и растяжение тригонометрических
функций
2024

2.

• Цель:
знать свойства тригонометрических функции.
Развивающие –вырабатывать навыки и умения
использовать полученные знания в построениях
графиков тригонометрических функций, развивать
математическое мышление учащихся, умение видеть и
применить изученные свойства, развивать умения
самостоятельной учебно-познавательной деятельности,
развивать культуру речи и любознательность

3.

4.

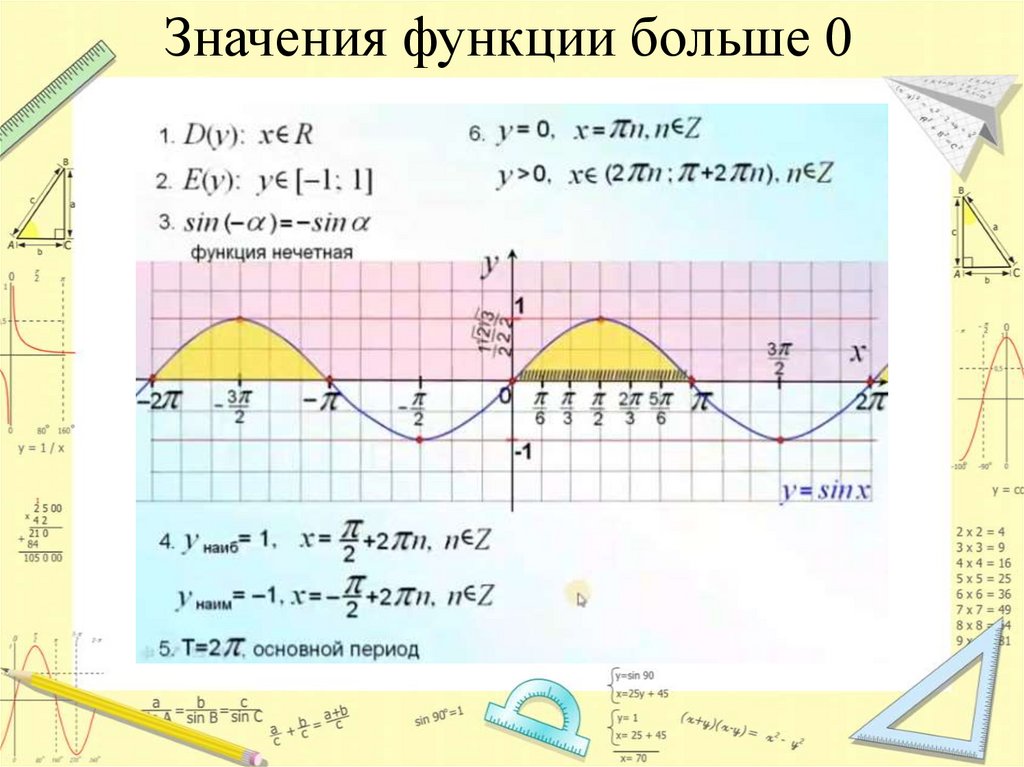
Значения функции больше 0

5.

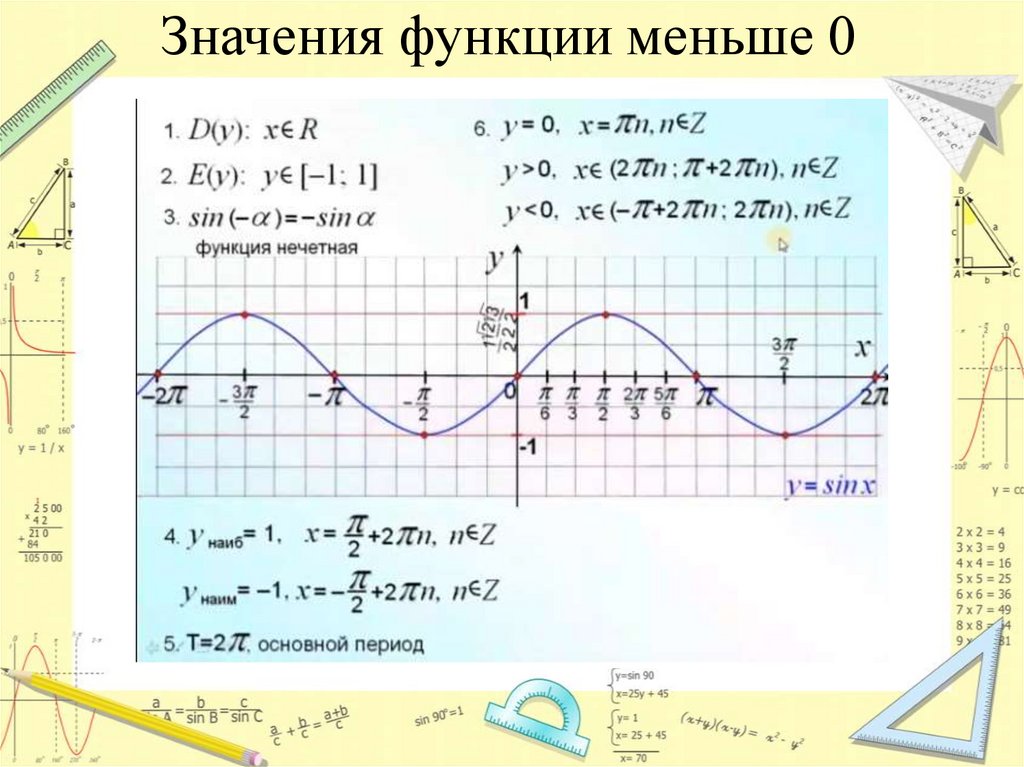
Значения функции меньше 0

6.

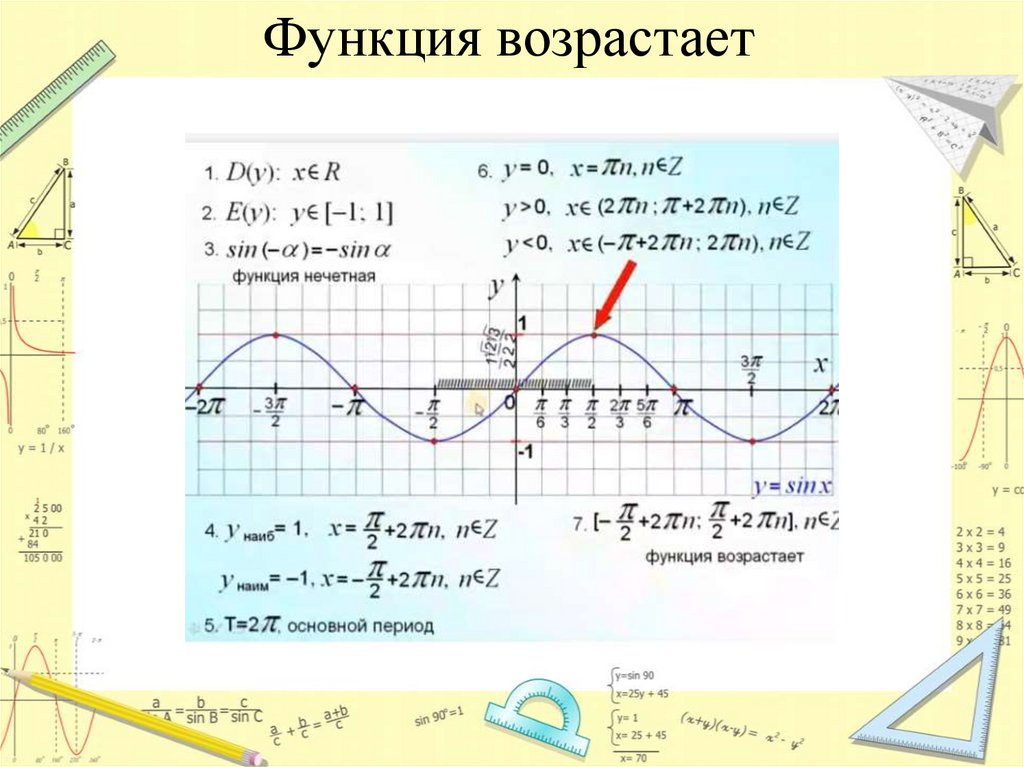
Функция возрастает

7.

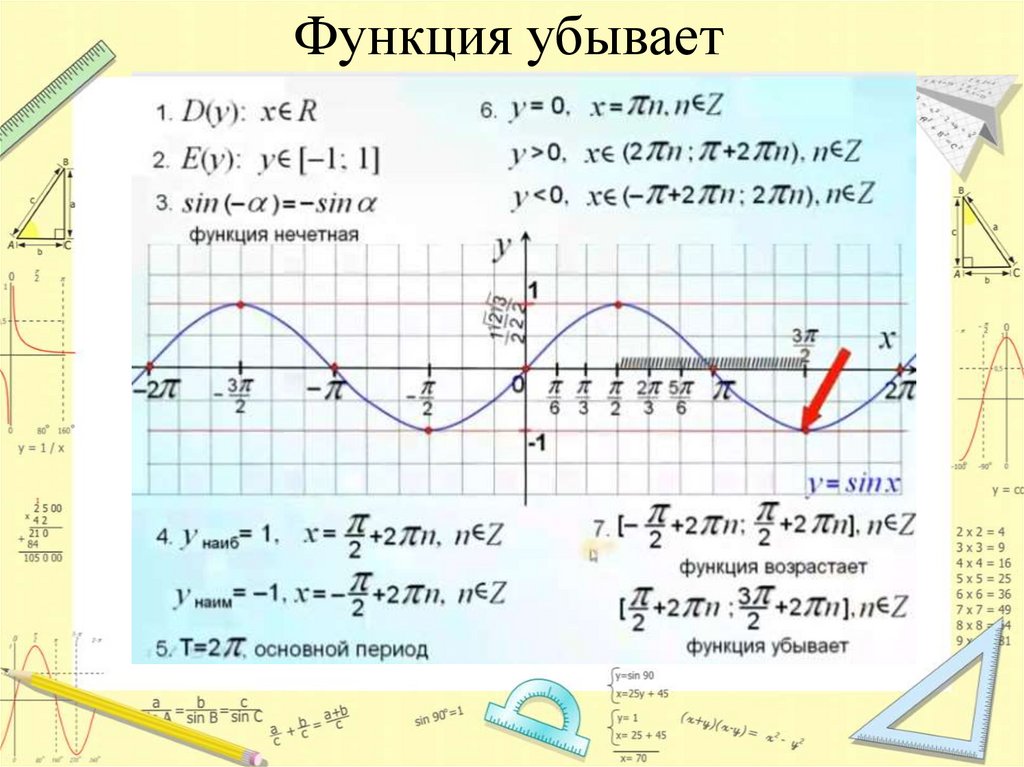
Функция убывает

8.

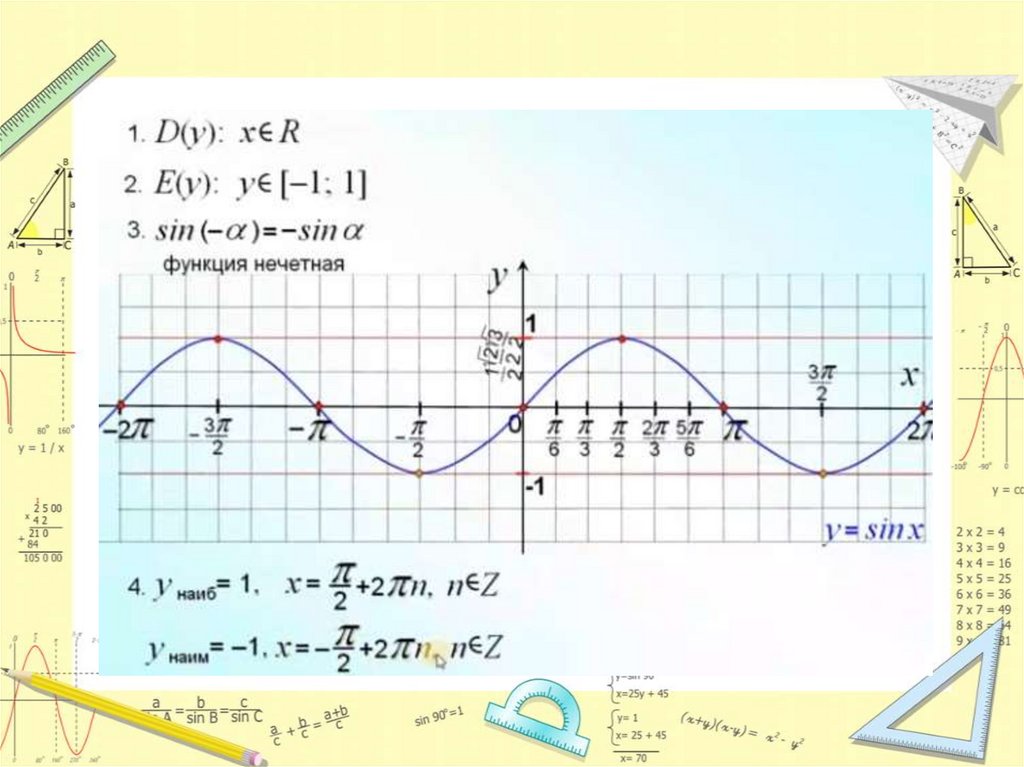
Функция у=sinx, её свойства и график
1.
D(y) = ( - ; + )
2.
Е = [-1; 1], т.е. синус функция — ограниченная.
3.
4.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
5.
Функция периодическая, T = 2π:
6.
sin x = 0 при x = π·k, k ∈ Z.
7.
sin x > 0 при x ∈ (2π·k, π+2πk), k ∈ Z.
8.
sin x < 0 при x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
9.
Функция возрастает при х
10.
11.
Функция убывает при х
Наибольшее значение функции sin x = 1 в точках:
Наименьшее значение функции sin x = −1 в точках:

9.

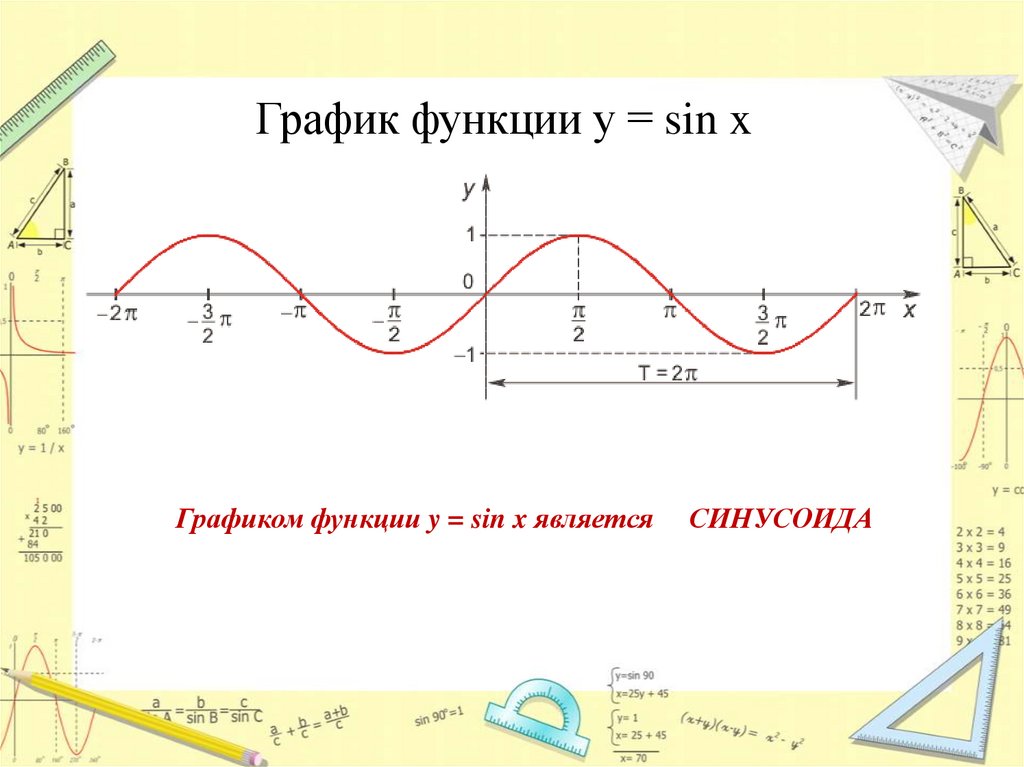
График функции у = sin x
Графиком функции y = sin x является
СИНУСОИДА

10.

Функция у=соs x, её свойства и график
1.
2.
3.
4.
5.
6.
D(y) = ( )
E= [-1; 1], т.е. косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая, Т = 2π:
cos x = 0 при
7.
cos x > 0 при
8.
cos x < 0 при
9.
10.
11.
12.
Функция возрастает при х ( - + 2 k 2 k)
Функция убывает при х (2 k; + 2 k)
Наибольшее значение функции x = 2 k, k
Наименьшее значение функции x = + 2 k, k

11.

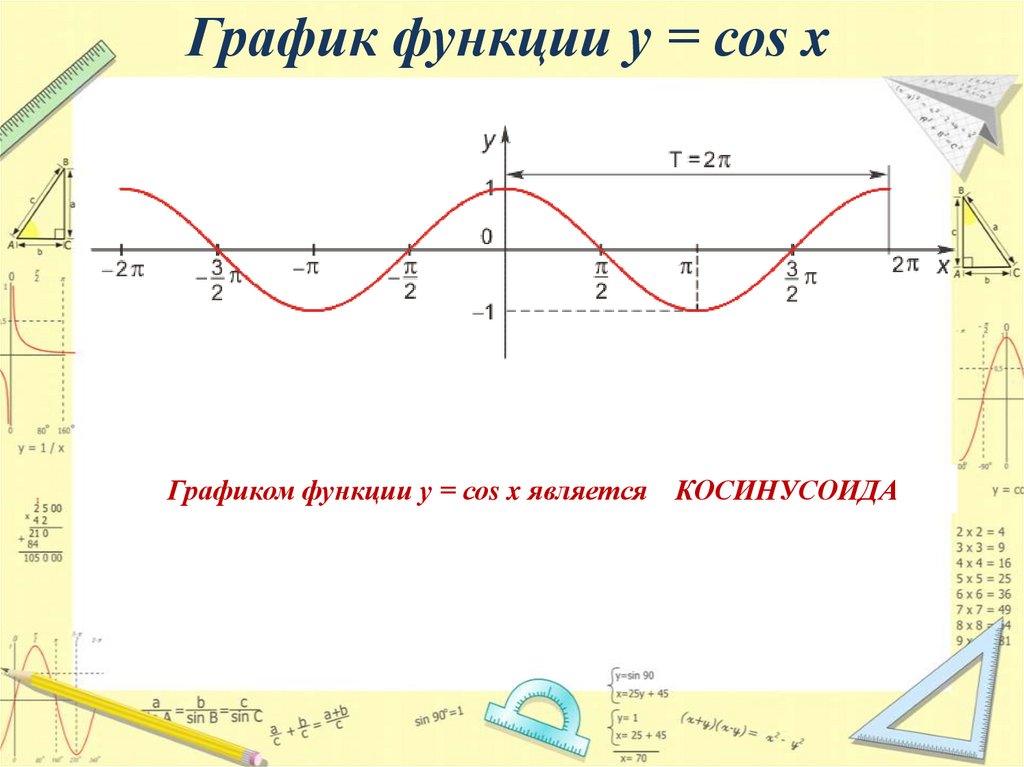
График функции у = соs x
Графиком функции у = соs x является КОСИНУСОИДА

12.

13.

14.

15.

16.

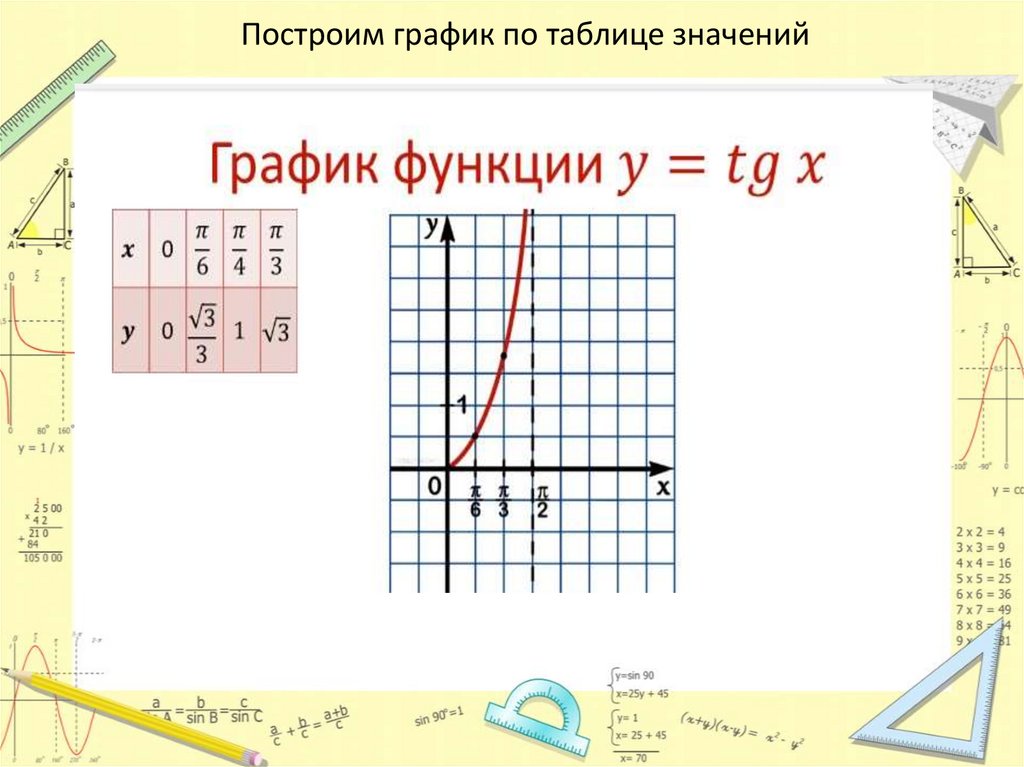
Построим график по таблице значений

17.

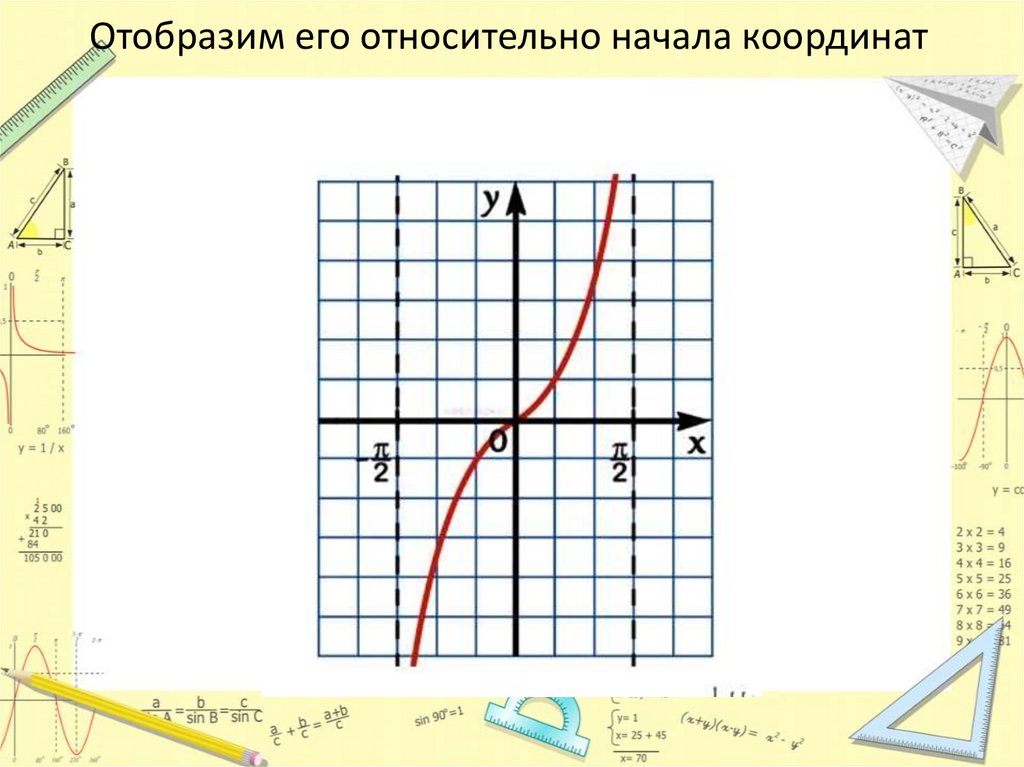
Отобразим его относительно начала координат

18.

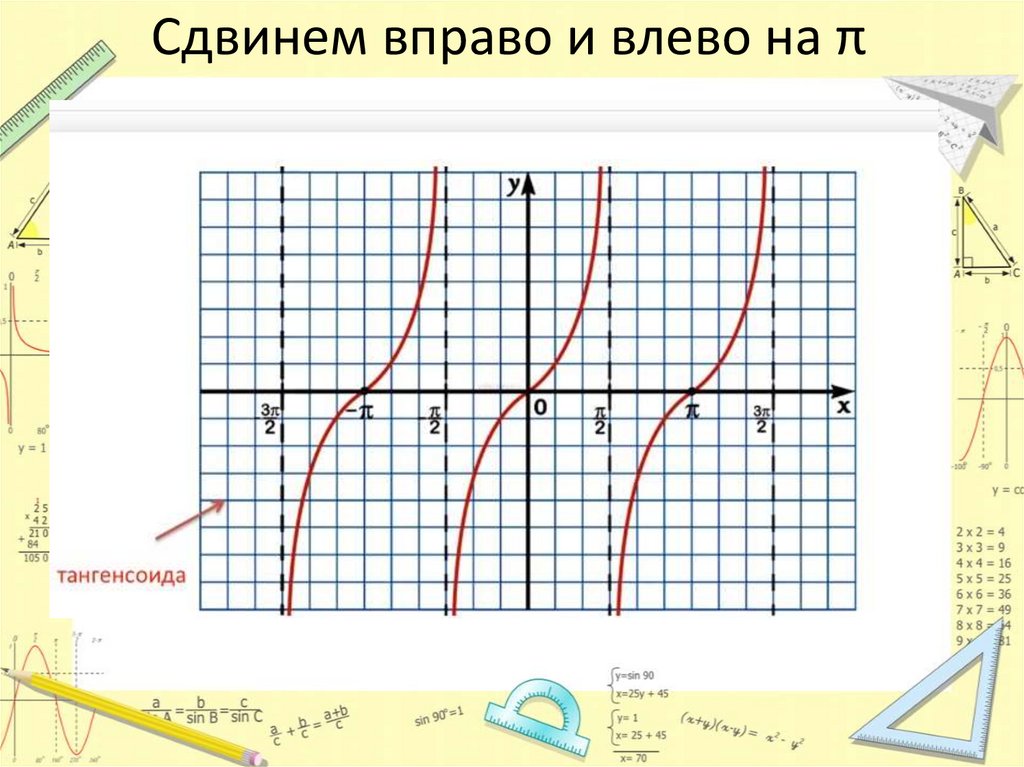
Сдвинем вправо и влево на π

19.

20.

21.

22.

23.

24.

25.

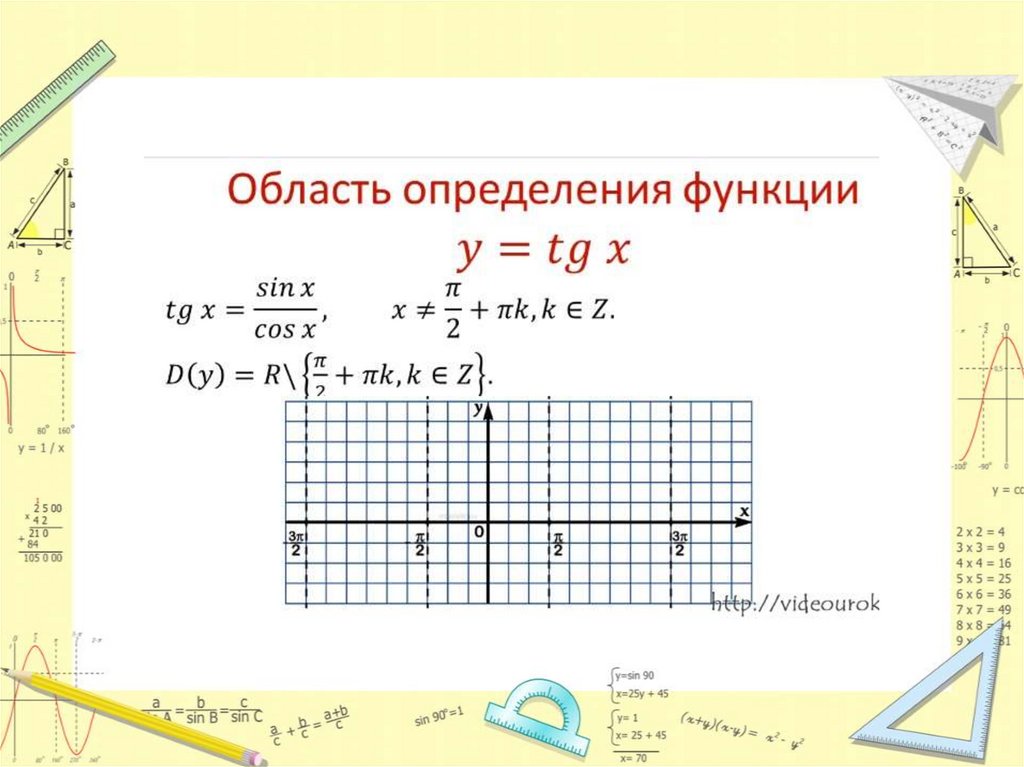
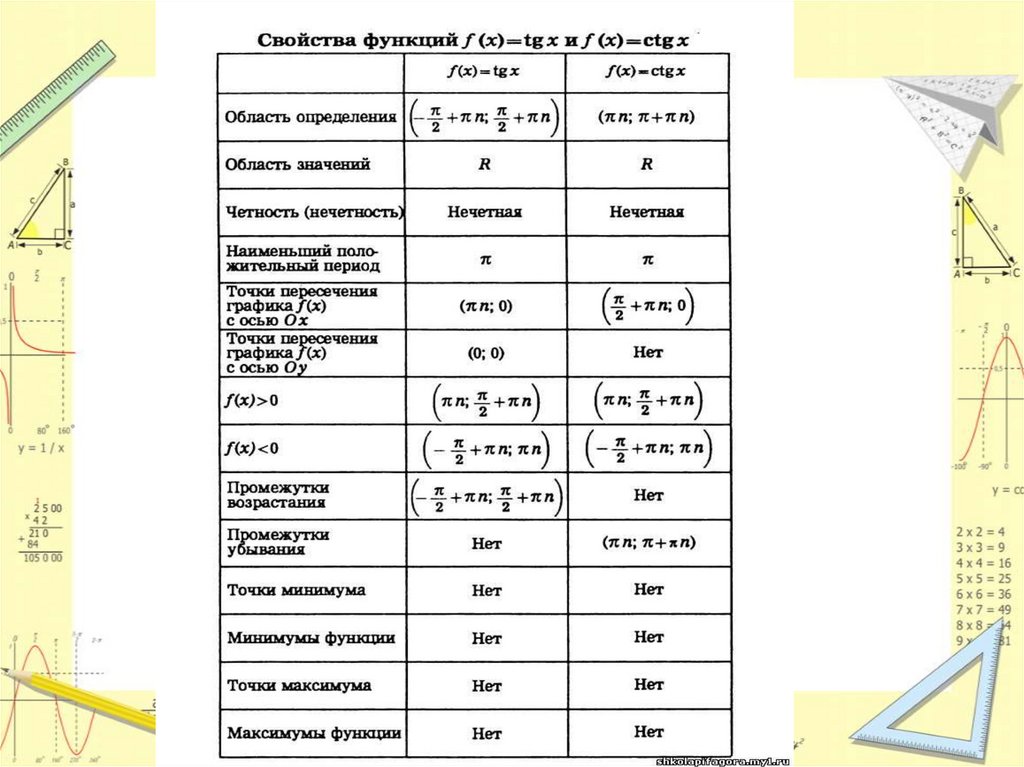
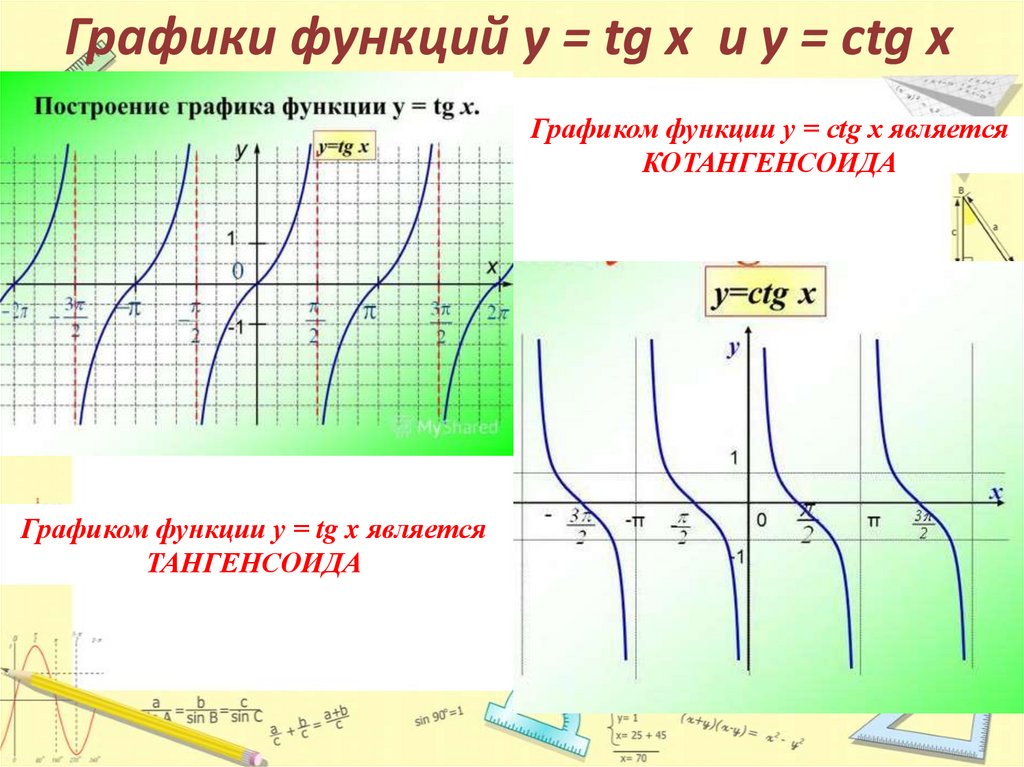
Графики функций у = tg x и y = ctg x
Графиком функции у = сtg x является
КОТАНГЕНСОИДА
Графиком функции у = tg x является
ТАНГЕНСОИДА

26.

Преобразование графиков функций

27.

Пусть задан график функции y = f(x)
Преобразование вида y = kf(x)
Преобразование вида y = f(x) + b
Преобразование вида y = f(x – a)
Преобразование вида y = f(mx)
Преобразование вида y = |f(x)|
Преобразование вида y = f(|x|)

28.

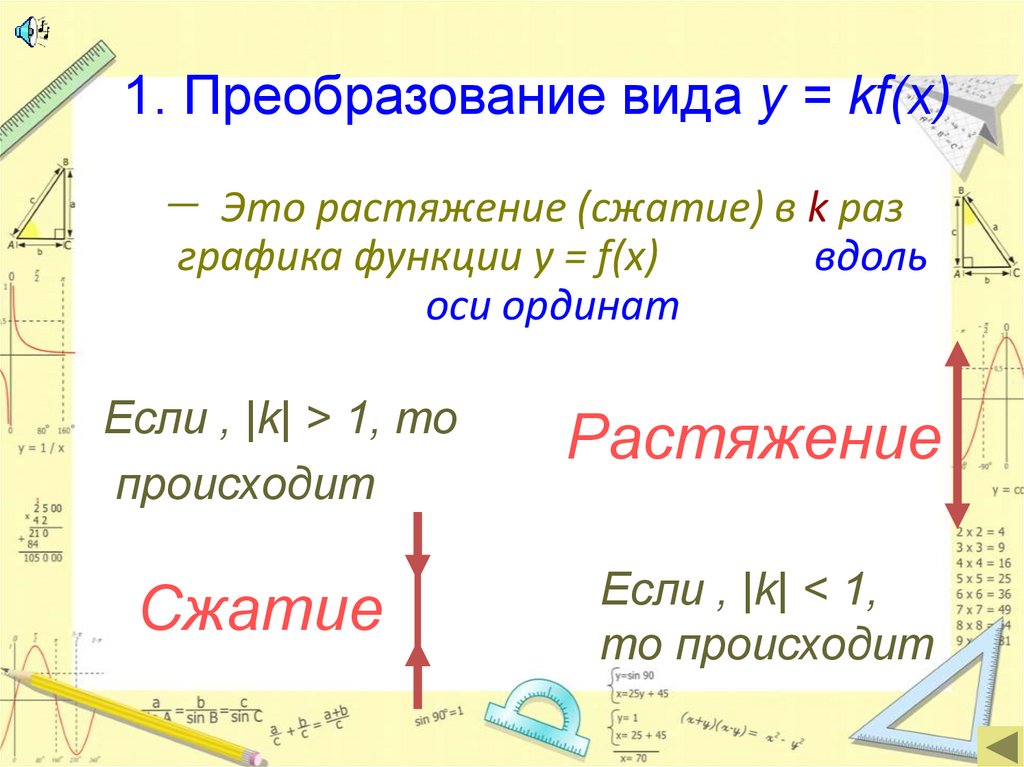
1. Преобразование вида y = kf(x)
— Это растяжение (сжатие) в k раз
графика функции y = f(x)
оси ординат
вдоль
Если , |k| > 1, то
происходит
Растяжение
Сжатие
Если , |k| < 1,
то происходит

29.

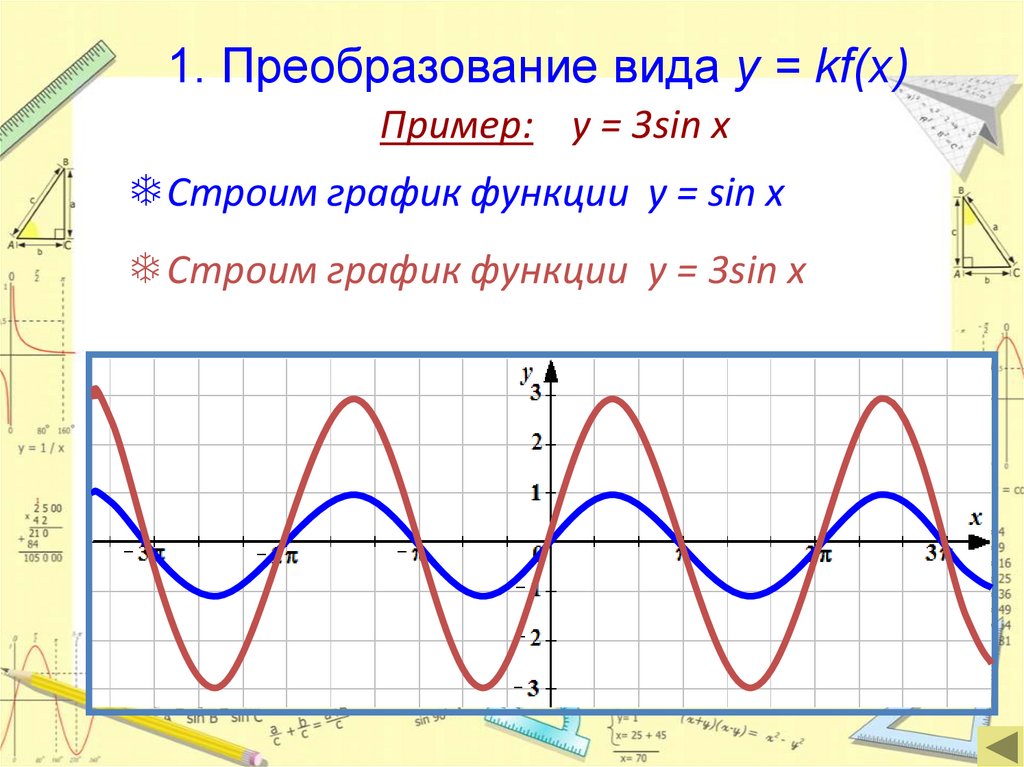
1. Преобразование вида y = kf(x)
Пример: y = 3sin x
Строим график функции у = sin x
Строим график функции у = 3sin x

30.

2. Преобразование вида y = f(x) + b
— Это параллельный перенос графика
функции y = f(x) на b единиц вдоль оси
ординат
Если b > 0, то
происходит
смещение
Если b < 0, то
происходит
смещение

31.

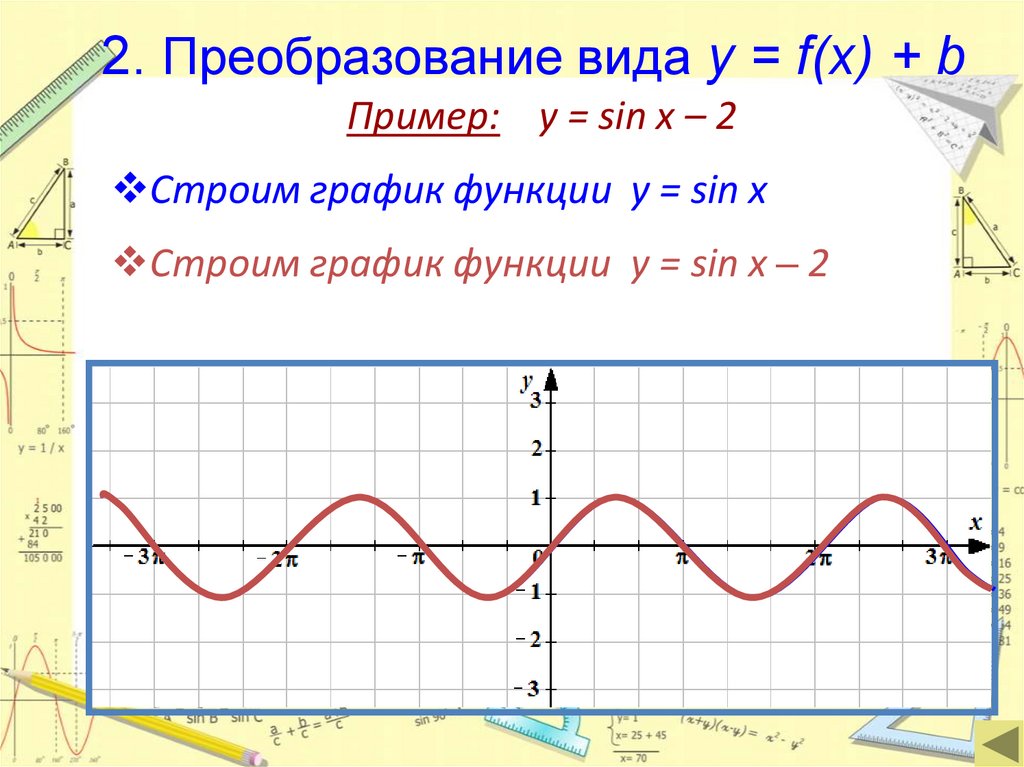
2. Преобразование вида y = f(x) + b
Пример: y = sin x – 2
Строим график функции у = sin x
Строим график функции у = sin x – 2

32.

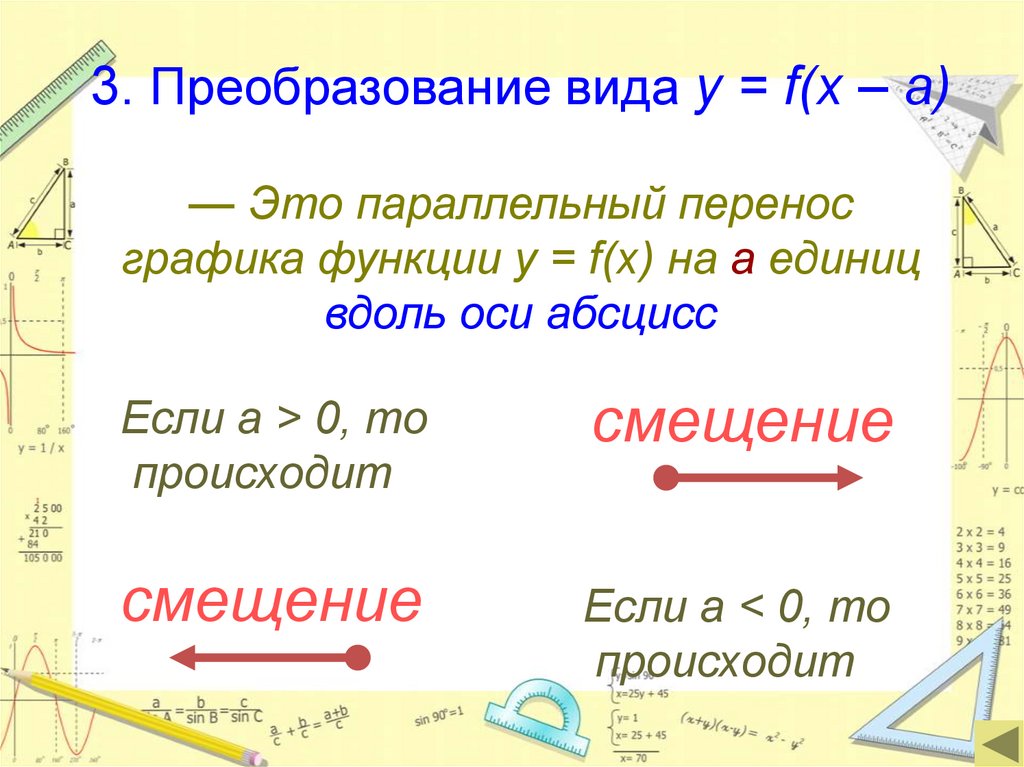
3. Преобразование вида y = f(x – a)
— Это параллельный перенос
графика функции y = f(x) на а единиц
вдоль оси абсцисс
Если а > 0, то
происходит
смещение
смещение
Если а < 0, то
происходит

33.

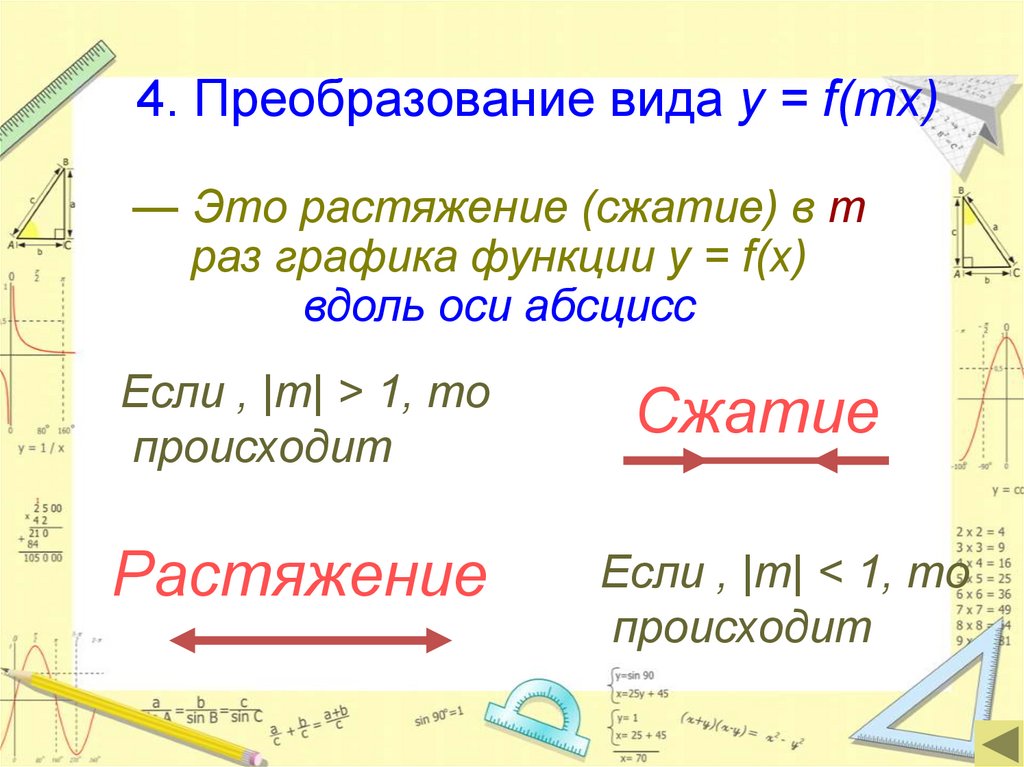
4. Преобразование вида y = f(mx)
— Это растяжение (сжатие) в m
раз графика функции y = f(x)
вдоль оси абсцисс
Если , |m| > 1, то
происходит
Сжатие
Растяжение
Если , |m| < 1, то
происходит

34.

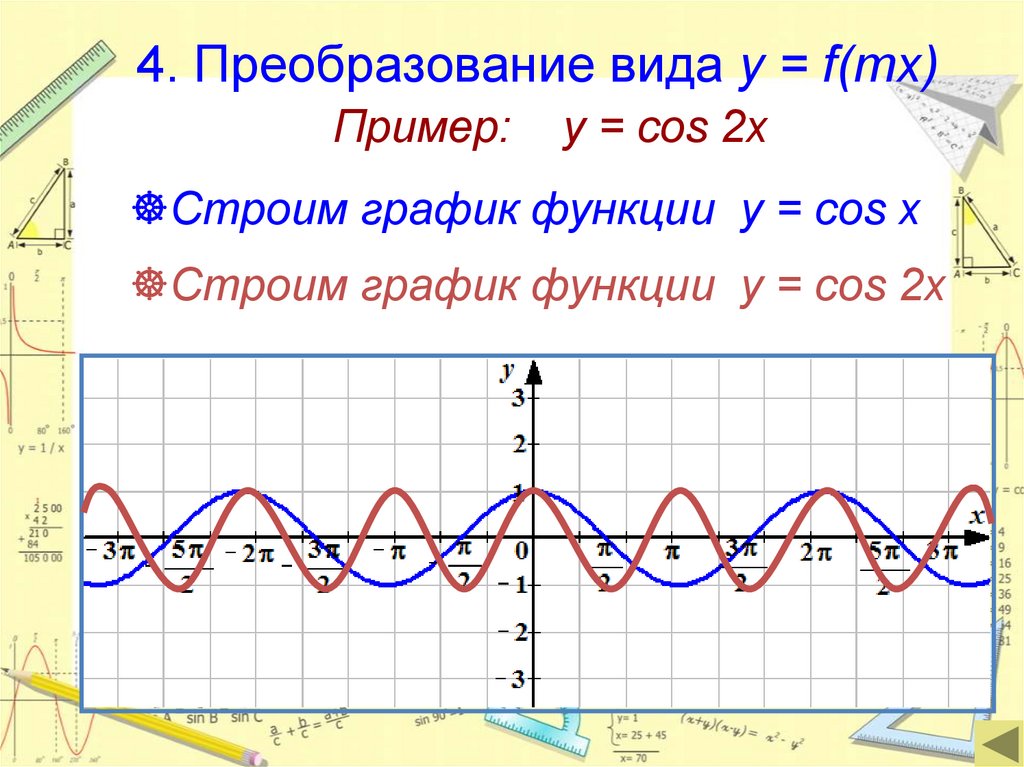
4. Преобразование вида y = f(mx)
Пример:
y = cos 2x
Строим график функции у = cos x
Строим график функции у = cos 2x

35.

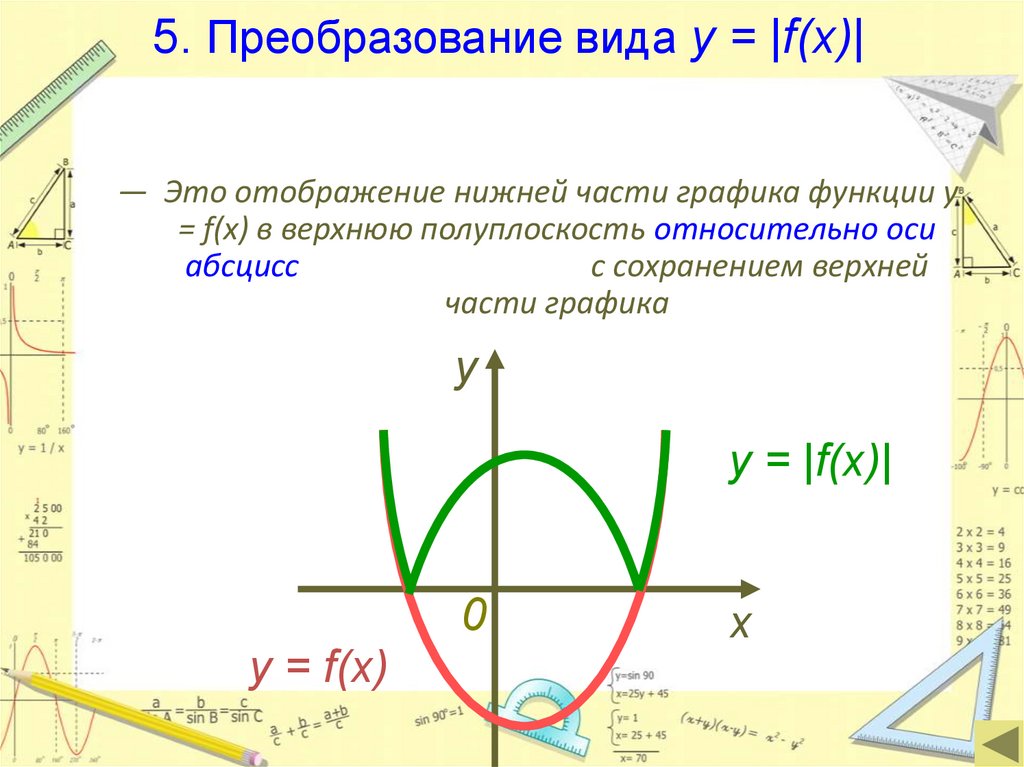
5. Преобразование вида y = |f(x)|
— Это отображение нижней части графика функции y
= f(x) в верхнюю полуплоскость относительно оси
абсцисс
с сохранением верхней
части графика
у
y = |f(x)|
y = f(x)
х
0

36.

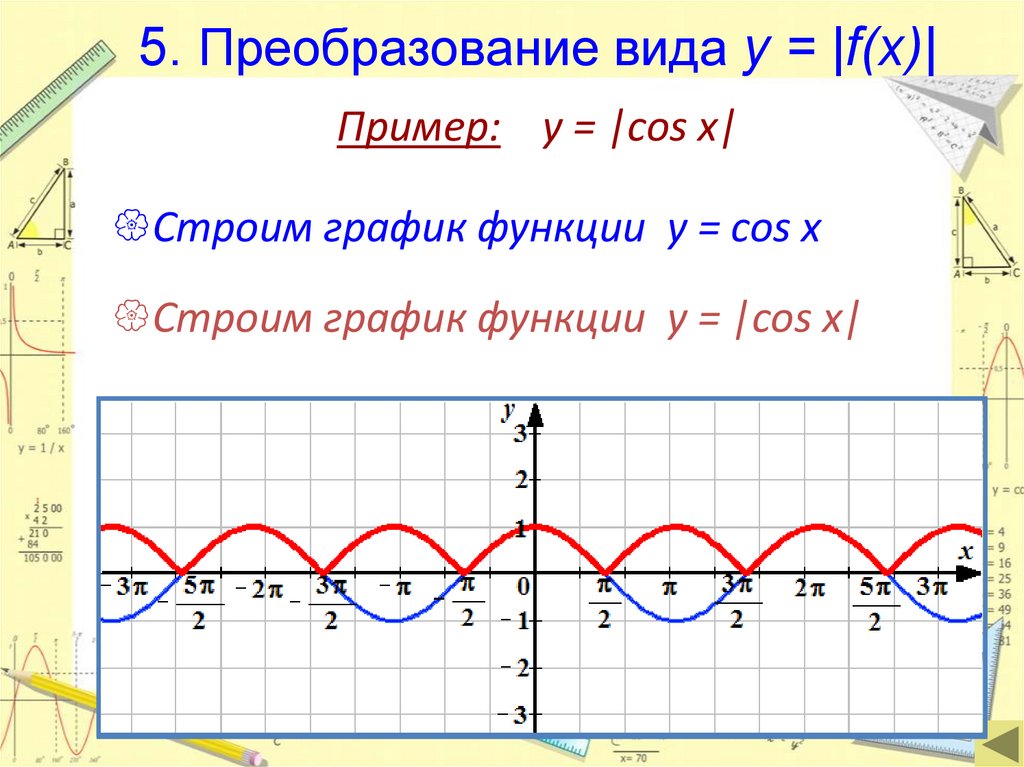
5. Преобразование вида y = |f(x)|
Пример: y = |cos x|
Строим график функции у = cos x
Строим график функции у = |cos x|

37.

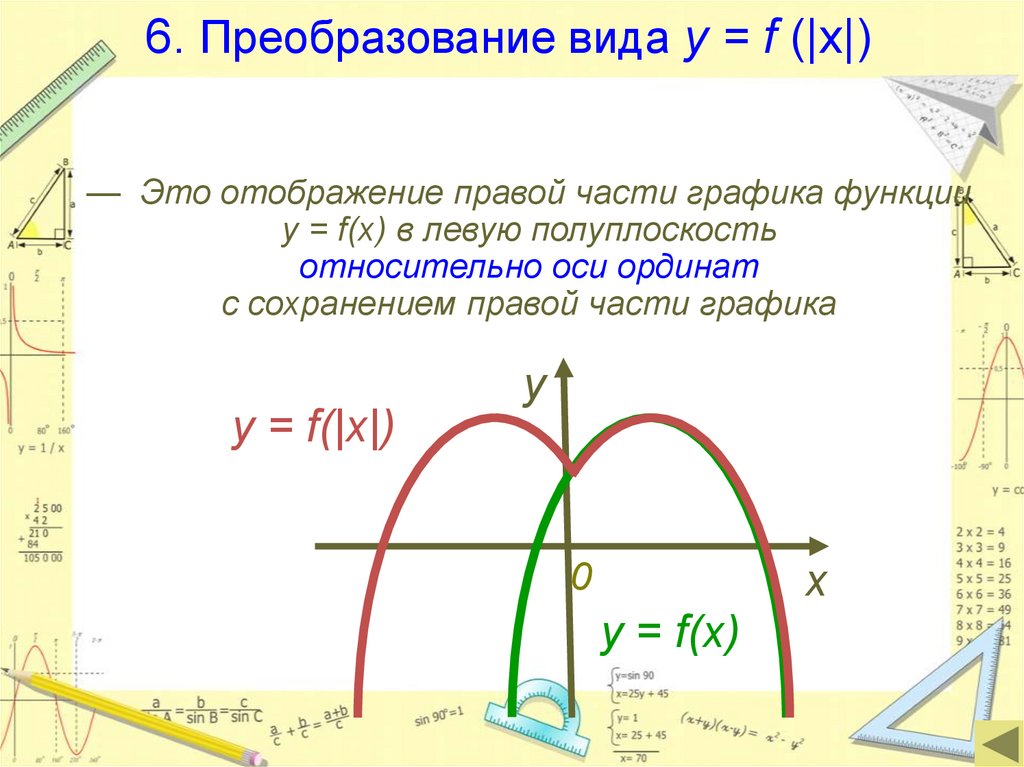
6. Преобразование вида y = f (|x|)
— Это отображение правой части графика функции
y = f(x) в левую полуплоскость
относительно оси ординат
с сохранением правой части графика
у
y = f(|x|)
х
0
y = f(x)

38.

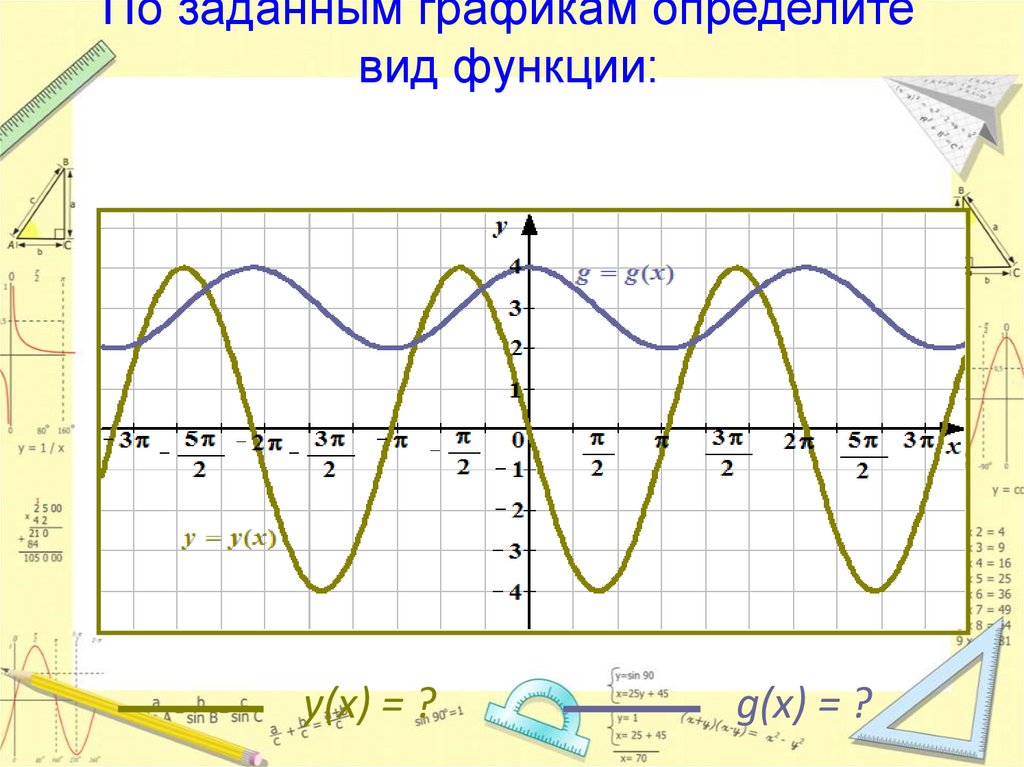
По заданным графикам определите
вид функции:
y(x) = ?
g(x) = ?

39.

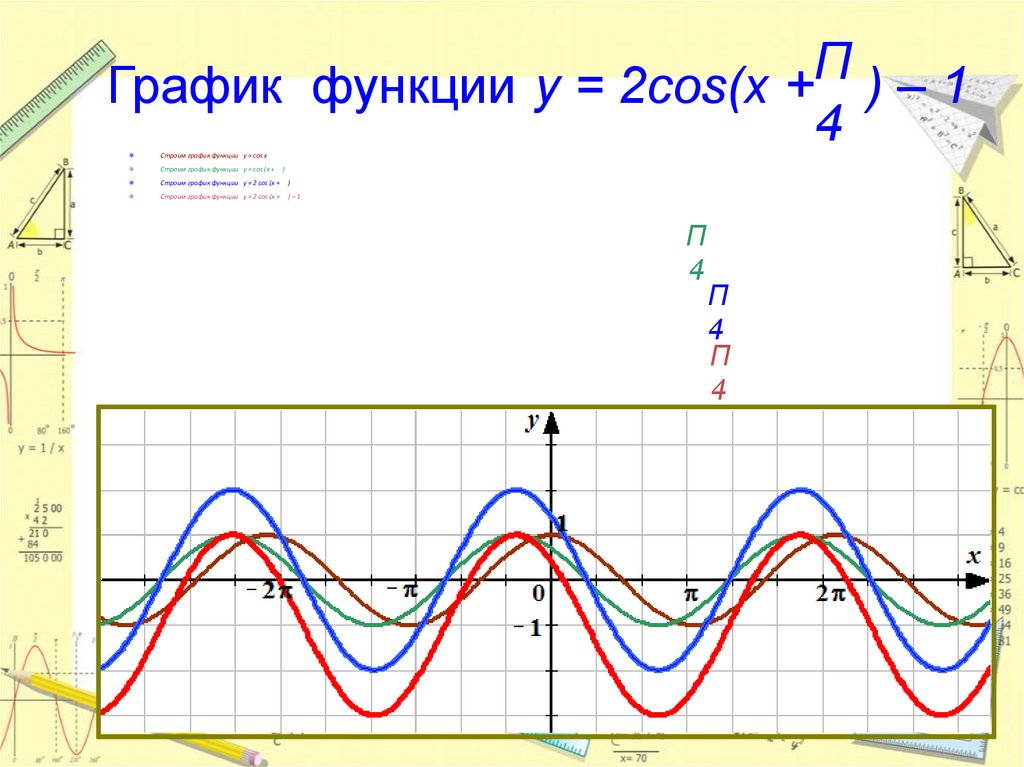
Π
График функции y = 2cos(x + ) – 1
4
Строим график функции y = cos x
Строим график функции y = cos (x +
Строим график функции y = 2 cos (x +
)
Строим график функции y = 2 cos (x +
)–1
)
Π
4
Π
4
Π
4