Обратно тригонометрические функции

1.

2.

«Функция, как правило, определяется
для тех значений аргумента, какие для
данной задачи представляют реальное
значение»
Хинчин А.Я.

3.

,
При каких значениях t верно равенство?
sint = 0,5
sint = 0,3
t=?

4.

Обратные
тригонометрические функции
у=arcctgx
у=arcsinx
график
график
у=arccosx
график
у=arctgx
график

5.

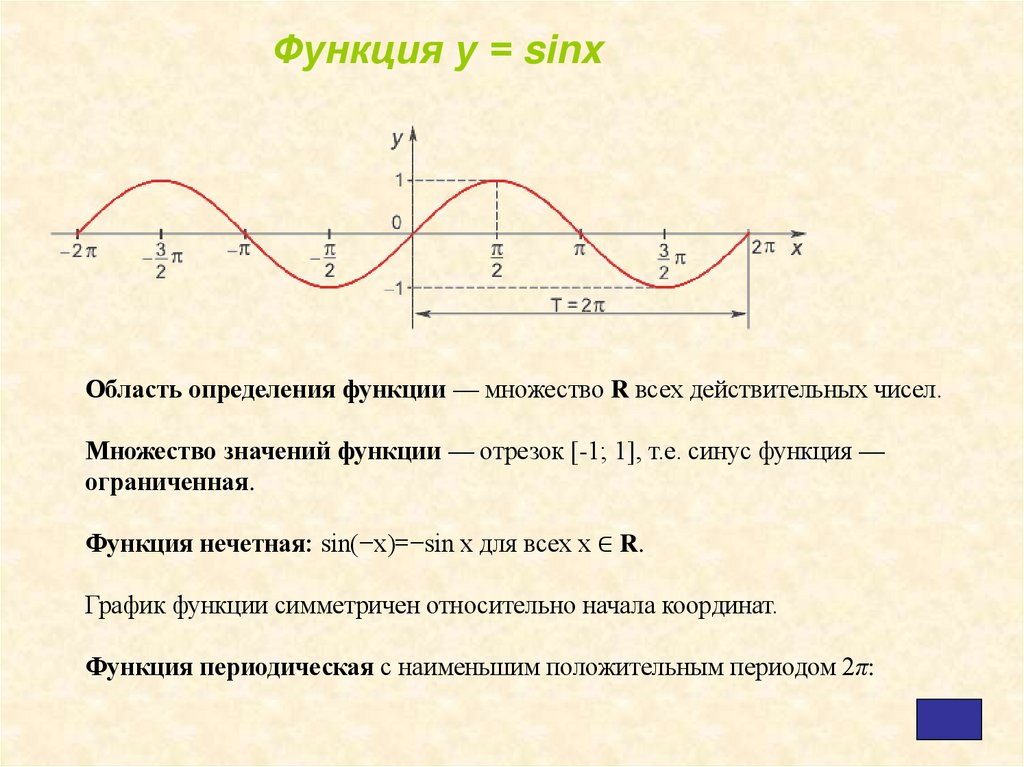
Функция у = sinx
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция —
ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:

6.

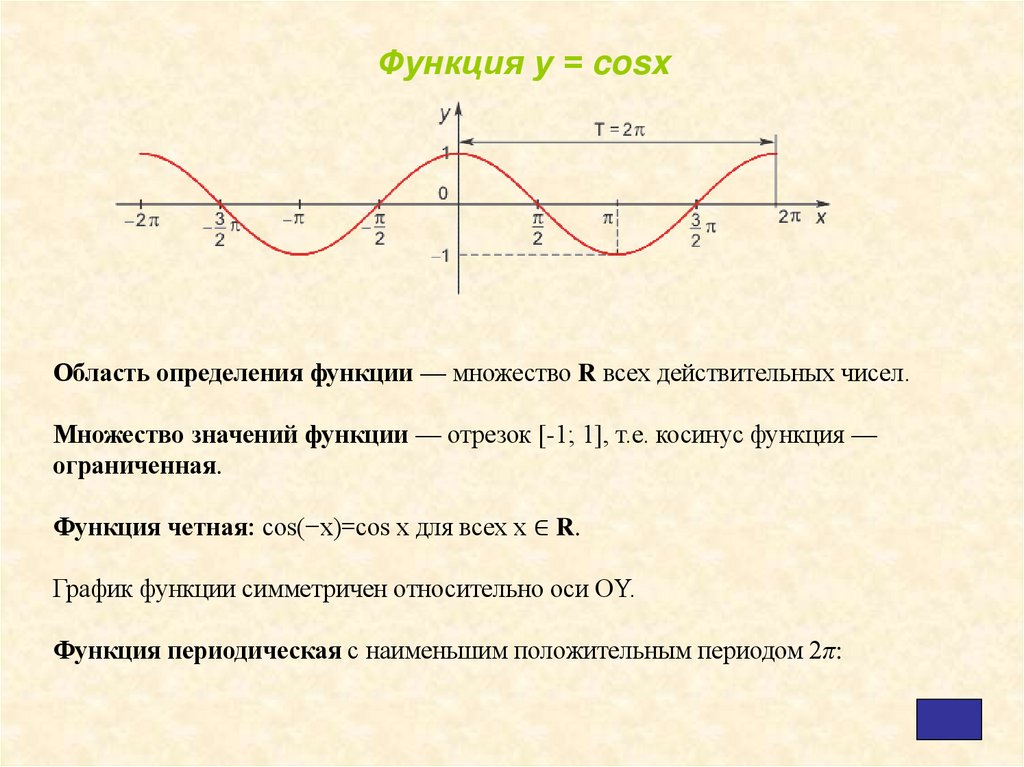
Функция у = cosx
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция —
ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:

7.

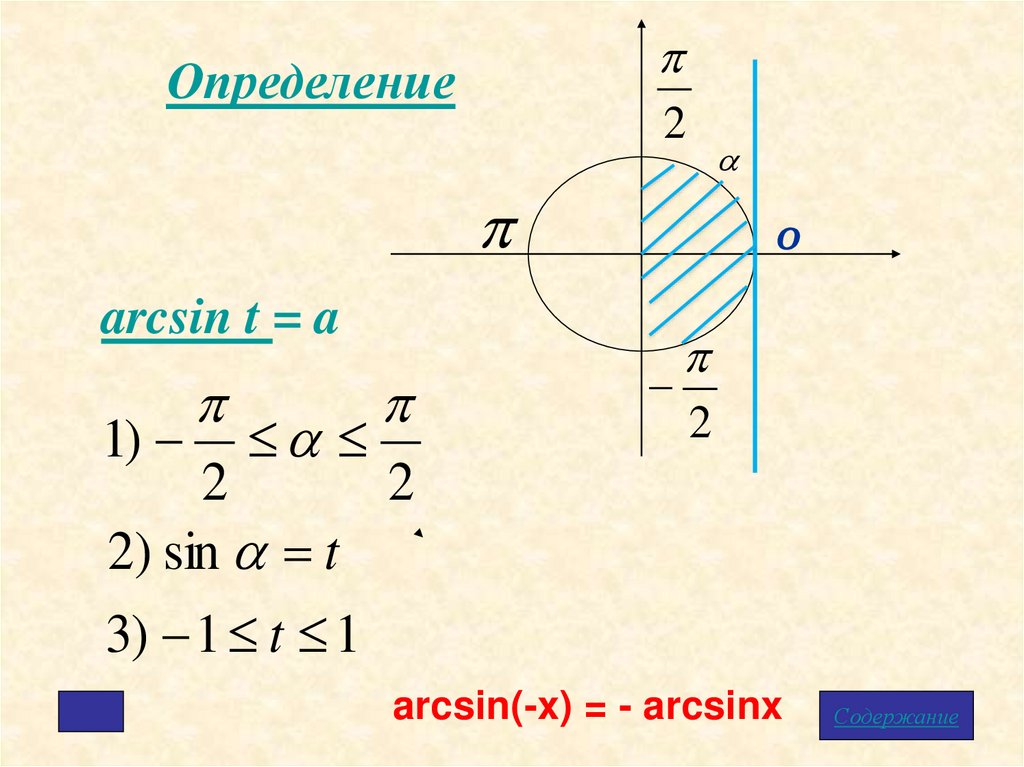
2
Определение
0
arcsin t = a
1)
2
2
2) sin t
3) 1 t 1
2
arcsin(-x) = - arcsinx
Содержание

8.

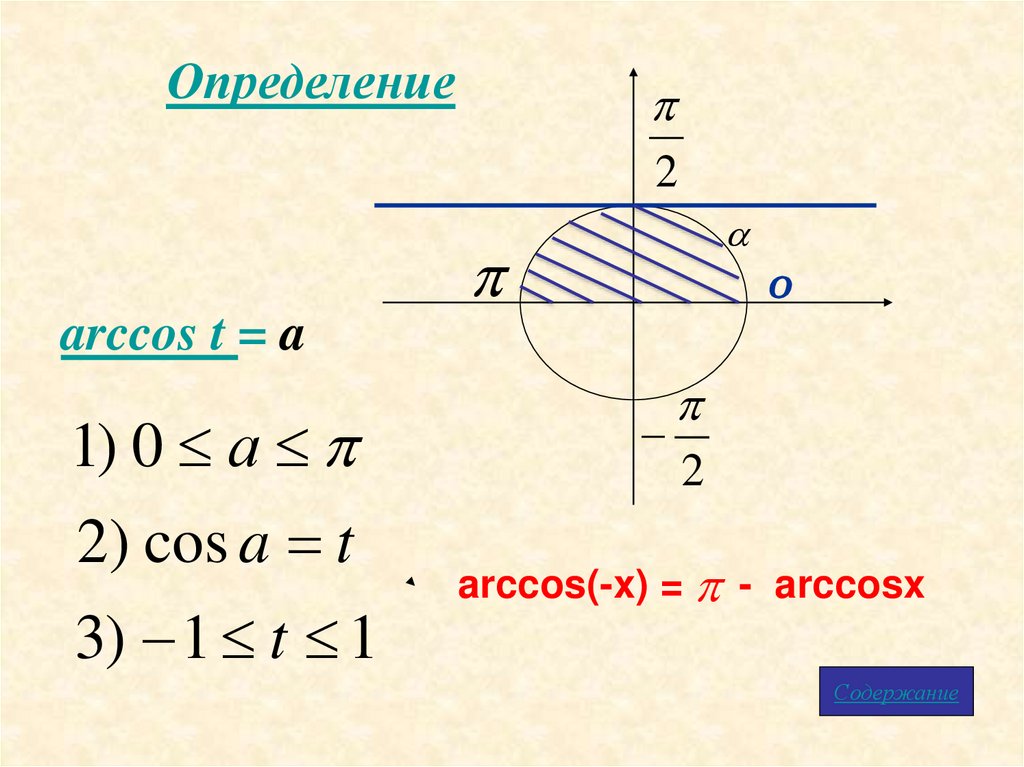
Определение
2
0
arccos t = a
1) 0 а
2) cos a t
3) 1 t 1
2
arccos(-x) = - arccosx
Содержание

9.

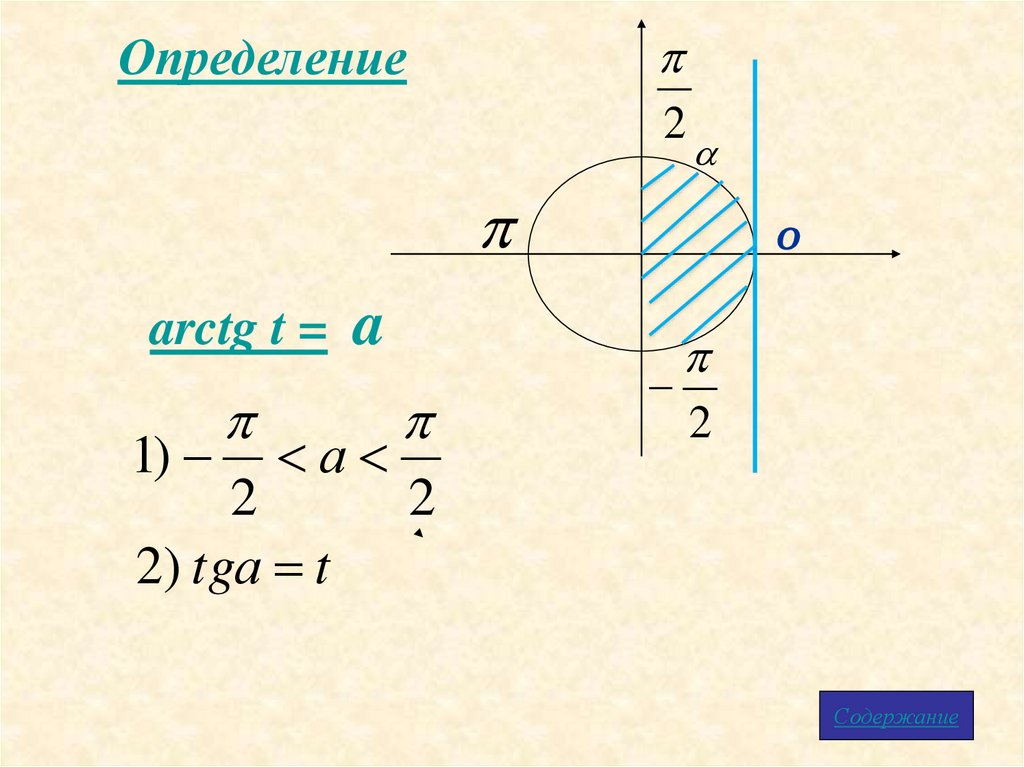
2
Определение
arctg t = a
1)
а
2
2) tgа t
0
2
2
Содержание

10.

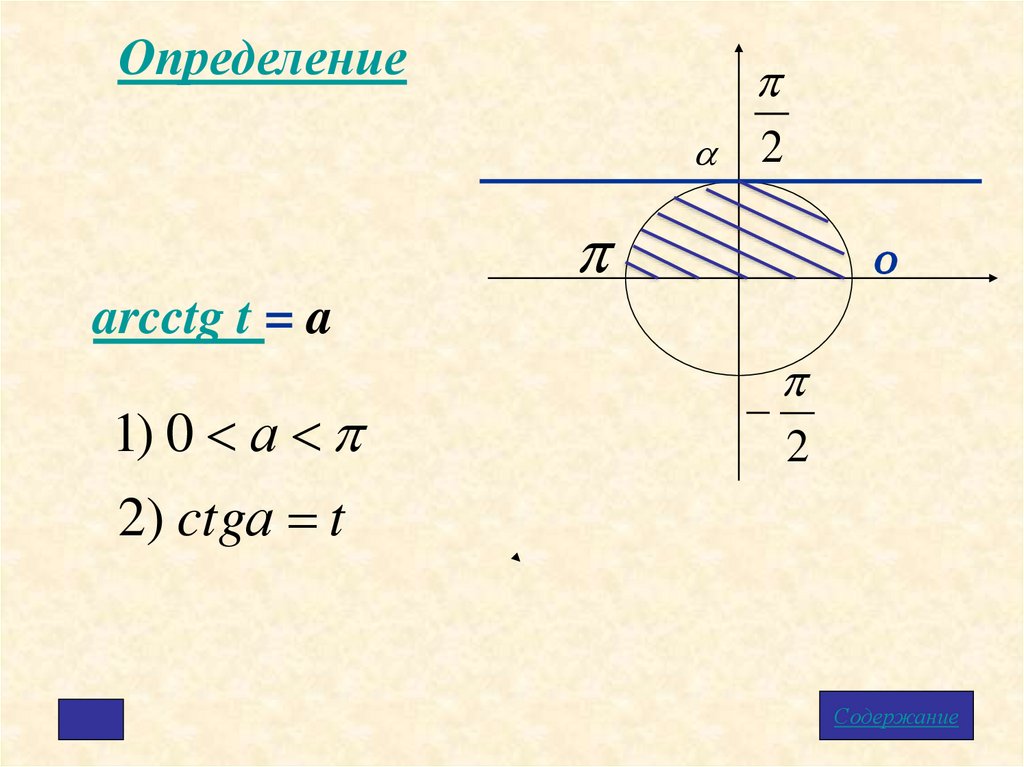
Определение
2
0
arcctg t = a
1) 0 а
2) ctgа t
2
Содержание

11.

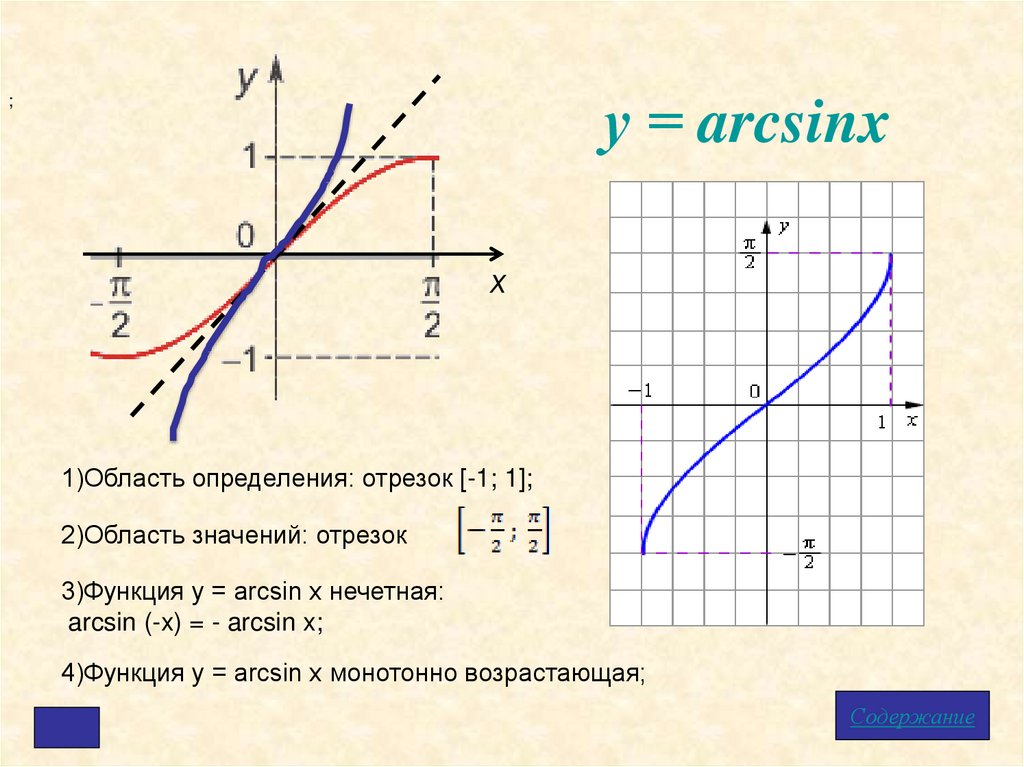
у = arcsinx
;
х
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция у = arcsin x монотонно возрастающая;
Содержание

12.

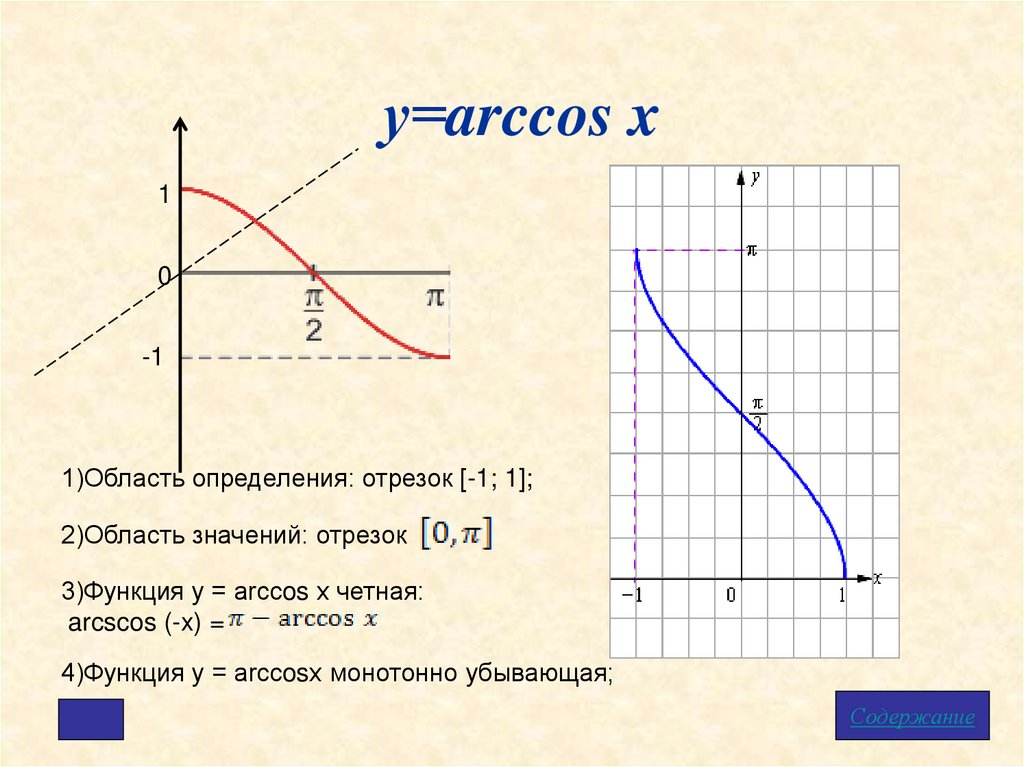
у=arccos x
1
0
-1
1)Область определения: отрезок [-1; 1];
2)Область значений: отрезок
3)Функция у = arcсos x четная:
arcscos (-x) =
4)Функция у = arcсosx монотонно убывающая;
Содержание

13.

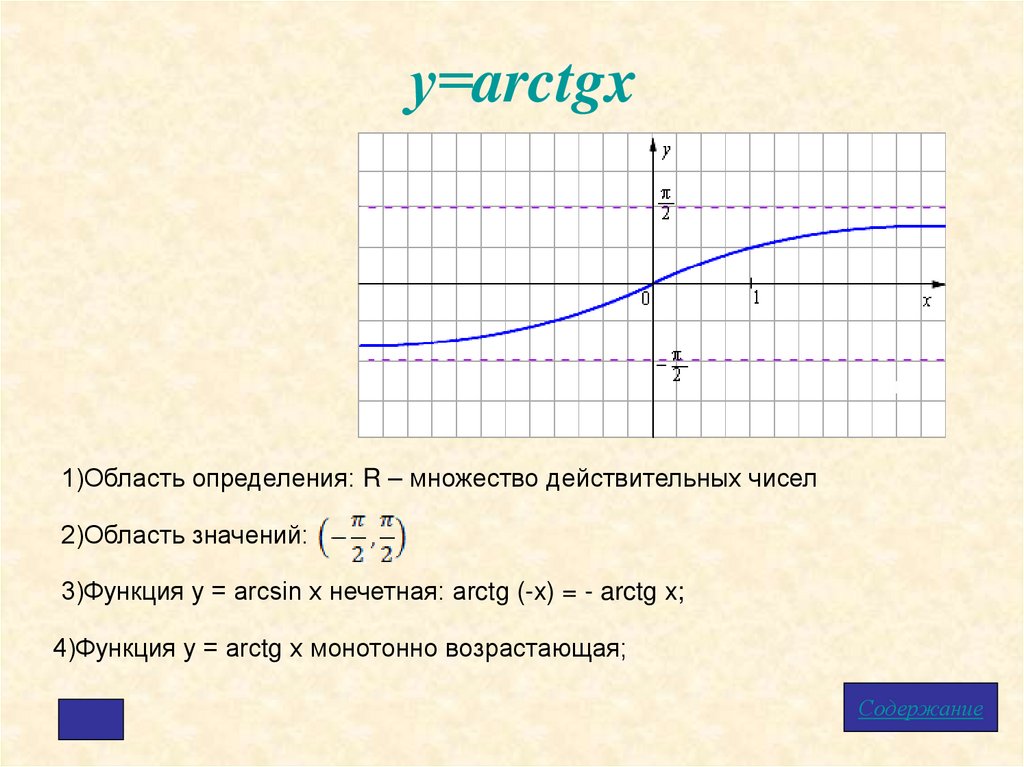
у=arctgx
1)Область определения: R – множество действительных чисел
2)Область значений:
3)Функция у = arcsin x нечетная: arctg (-x) = - arctg x;
4)Функция у = arctg x монотонно возрастающая;
Содержание

14.

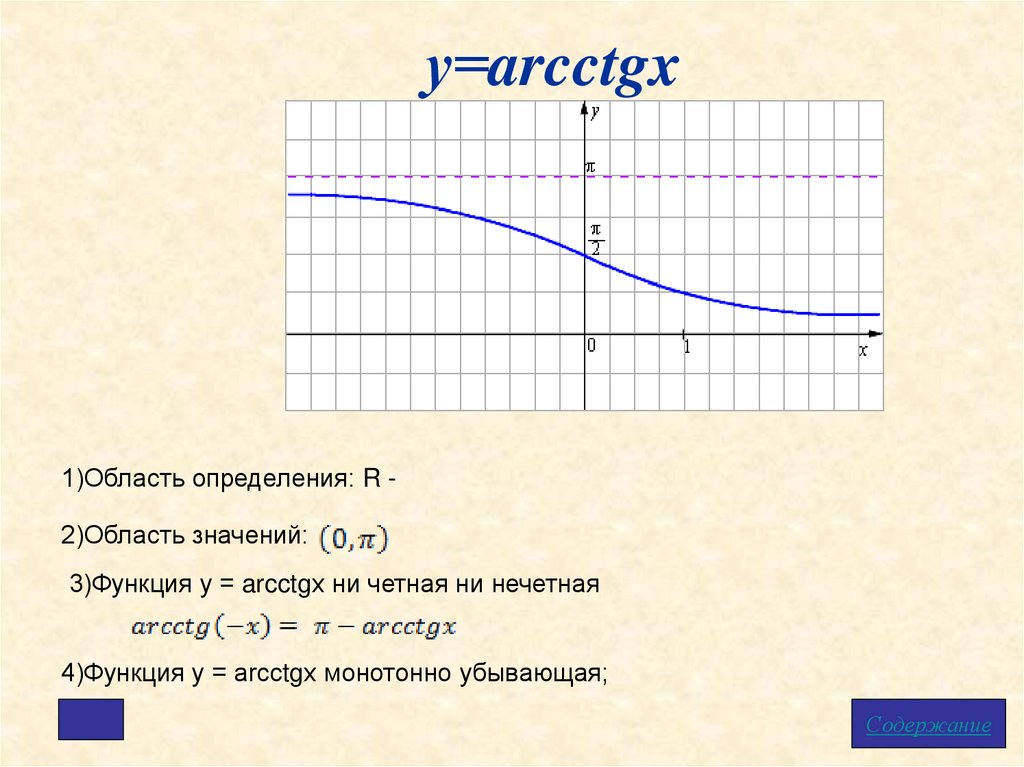
у=arcctgx
1)Область определения: R 2)Область значений:
3)Функция у = arcctgх ни четная ни нечетная
4)Функция у = arcсtgx монотонно убывающая;
Содержание

15.

Работаем устно
Имеет ли смысл выражение?
arcsin 2 arccos 3
arctg100
Может ли arcsint и arccost принимать
значение равное
5
5, , , 10,
9
3
,?
7
Содержание

16.

Свойства аркфункций
cos(arccos x ) x,
sin(arcsin x ) x,
tg ( arctgx) x
ctg ( arcctgx) x
arccos(cos x) x, x 1;1
arcsin(sin x) x, x 1;1
arctg (tgx) x,
arcctg (ctgx) x.

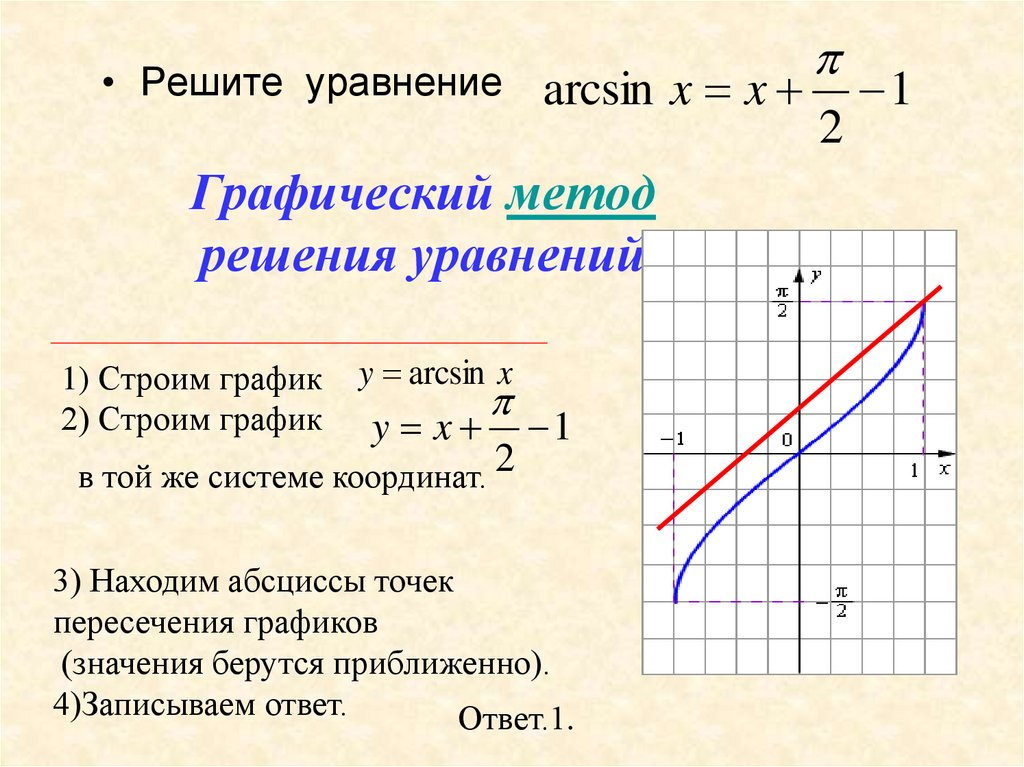
17. Графический метод решения уравнений

• Решите уравнение
arcsin x x
Графический метод
решения уравнений
1) Строим график
2) Строим график
y arcsin x
y x
в той же системе координат. 2
1
3) Находим абсциссы точек
пересечения графиков
(значения берутся приближенно).
4)Записываем ответ.
Ответ.1.
2
1

18.

Функционально-графический
метод решения уравнений
Пример: решите равнение
arccos x
Решение.
2
x
1) у =arccosx убывает на области определения
2 g x
x, возрастает на D,
2
3) Уравнение f(x)=g(x) имеет не более одного
корня.
4) Подбором находим, что x=0.
Ответ. 0.
Содержание