Квантильная регрессия. Выпускная квалификационная работа

1. Квантильная регрессия Выпускная квалификационная работа

Работу выполнила:
студентка ПМИ -3,4-09 группы IV курса
механико-математического факультета
Костенко Валентина Олеговна
Научный руководитель:
к. ф.-м. н., доцент
Бабушкина Елена Вадимовна

2. Цель и задачи:

Цель:
Цель и задачи:
определить условия применимости модели квантильной регрессии.
Задачи:
2
обзор различных подходов к решению задач регрессионного анализа
обзор различных подходов к решению задач регрессионного анализа
знакомство с теоретическими основами «бутстрапирования»;
реализация различных методов регрессии и бутстрап-метода в пакете R;
построение доверительных интервалов c помощью бутстрап-метода;
создание программного продукта, для автоматизации процесса построения
доверительных интервалов и построения моделей классической и
непараметрической регрессии для различных данных.
сравнение квантильной регрессии с классической моделью линейной
множественной регрессии при различных распределениях данных и
определение условий применимости квантильной регрессии

3.

Подходы к решению задач регрессионного анализа
Пусть имеется случайная выборка ( xi , yi ) in 1 из популяции пар (x,y)
Для оценивания регрессии среднего чаще всего пользуются
параметрическими методами, когда предполагается, что регрессионная функция
имеет известную функциональную форму и конечное число неизвестных
параметров
Модель классической линейной регрессии:
(1)
yi xiT i , E[ yi | xi ] xiT
где εi – случайные ошибки, имеющие непрерывное распределение
Предположения модели:
3
1)
M [ i ] 0
2)
D[ i ] 2 const
3)
K ( i , j ) 0
4)
i ~ N (0, 2 )
Для оценки неизвестных параметров
регрессионной модели используется
МНК, основанный на минимизации
суммы квадратов остатков регрессии

4.

Непараметрическая регрессия:
Ядерное сглаживание: при оценивании избегают
параметрических предположений о функциональной форме.
1 u
Ядерная функция K(u) : K (u )du 1 , K h (u ) K , h-ширина окна
k h
i 1 yi K h ( xi a)
n
Оценка Надарая-Ватсона g:ˆ (a)
i 1 K h ( xi a)
n
(2)
1
u2
Гауссово ядро : K (u )
exp( )
2
2
Квантильная регрессия: процедура оценки параметров линейной
регрессии для любого из квантилей интервала от 0 до 1.
Модель :
yi xiT u i , Quant ( yi | xi ) xiT
(3)
u- случайные
ошибки
i
Quant ( yi | xi ) - условная квантиль yi на векторе регрессора xi
Предположение модели : Quantθ(uθi|xi ) 0
4

5. Бутстрап-метод

1) Приближение бутстрапом:приближение истинного распределения
данных эмпирическим
2) Приближение симуляциями
исходная выборка
• z1 ,..., z—
n
—
) бутстрапируемая статистика
• ˆ ˆ ( z1 ,..., z n
•B - количество будущих бутстраповских выборок
z ,..., z
ˆ ˆ ( z ,..., z )
для
• b=1,2…B строим
вычисляем
*
b
*
1
*
1
*
n b
*
n
b
• ˆ1* ,..., ˆ B * с весами1/B — бутстраповское распределение статистики
̂
3) Рецентрирование
бутстрапируем
разность ˆ ,
ˆ — оценка параметра
правильный
бутстраповский аналог разности ˆ :
• ˆ* — бутстраповская статистика
5
ˆ* ˆ

6. Бутстрап-метод

1) Приближение бутстрапом:приближение истинного распределения
данных эмпирическим
2) Приближение симуляциями
исходная выборка
• z1 ,..., z—
n
—
) бутстрапируемая статистика
• ˆ ˆ ( z1 ,..., z n
z ,..., z , B — количество бутстраповских выборок
для
• b=1,2…B строим
*
1
*
n
b
ˆb * ˆ ( z1* ,..., z n * b )
вычисляем
• ˆ1* ,..., ˆ B * с весами1/B — бутстраповское распределение статистики
̂
• Находим бутстраповскую квантиль:q1* |% t |
• Бутстраповский симметричный t-процентильный доверительный
интервал:
6
.
CI |%t| [ ˆ se( ˆ)q1* |% t| , ˆ se( ˆ)q1* |% t| ]

7.

3) Рецентрирование
– аналоговая оценка
бутстрапируем разность ˆ , ˆ
параметра
• правильный бутстраповский аналог разности ˆ : ˆ* ˆ
(3)
(4)
неправильный бутстраповский аналог разности ˆ : ˆ*
4) Бутстраповская корректировка смещения
ˆ - состоятельная оценка параметра , причем E[ ]
смещение оценки B[ ˆ] E[ ˆ]
B *[ ˆ] E *[ ˆ* ] ˆ - бутстраповский аналог смещения
E *[ ˆ* ] - математическое ожидание по отношению к эмпирической
функции распределения
cтатистика, скорректированная на смещение: :
ˆBC ˆ B*[ ˆ] 2 ˆ E*[ ˆ* ]

8.

3) Бутстраповская инференция

9.

5) Бутстраповская инференция
Построение статистических выводов о параметре на
основе его состоятельной оценки ˆ .
• Пробутстрапируем статистику
ˆ / se( ˆ) : ˆ* ˆ / se* ( ˆ)
(5)
9

10.

Экспериментальное определение условий
применимости модели квантильной регрессии
Описание эксперимента.
yij – сгенерированное значение, i – номер выборки, j – номер
значения в выборке.
xij 0 - индикатор, указывающий на «хорошие» значения
xij 1 - индикатор, указывающий на «плохие» значения
30% процентов значений каждой выборки -"плохие".
yij xij ij - линейная зависимость
Число бутстраповских выборок 1000, число значений в выборке n= 500.
4 типа смеси распределений :
bad
1) ~y good ~ N(300;150) и ~y ~ N(450;150)
bad
~
good
~
y
~ Gamma(9;50)
y
~
Gamma(
4
;
75
)
и
2)
~
~
y bad ~ Gamma(0.334;1352)
y good ~ Gamma(0.334;900)
3)
и
4) ~y good ~ Pareto(160;2.15) и ~y bad ~ Pareto(240;2.15)
10

11.

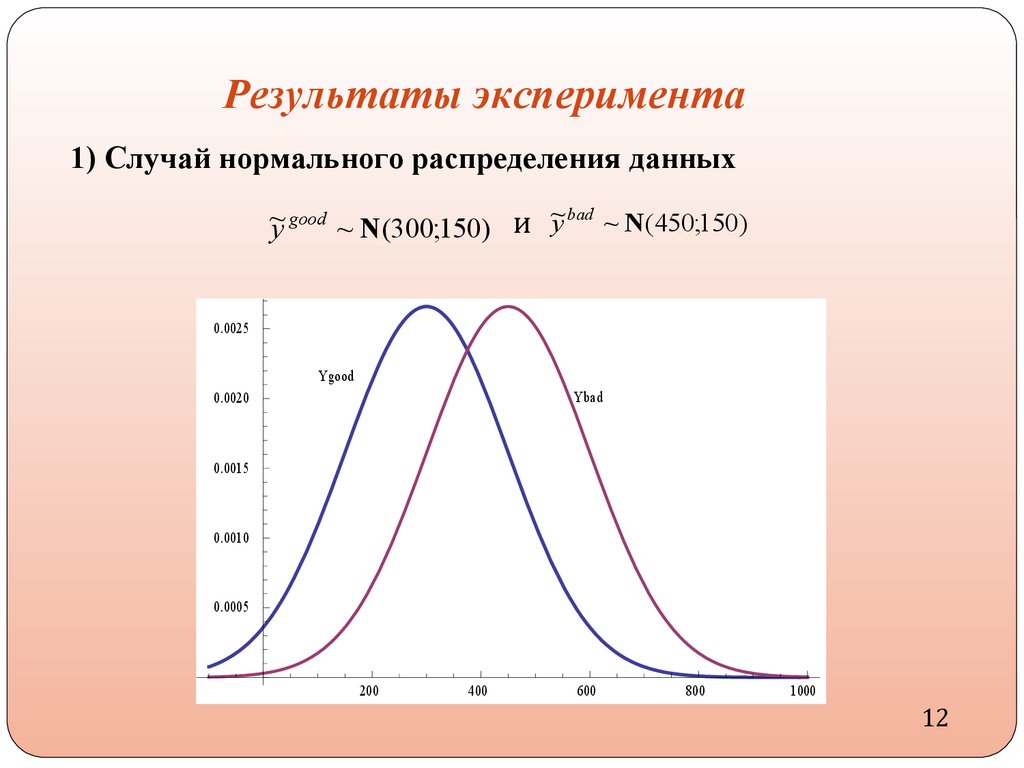
Результаты эксперимента
1) Случай нормального распределения данных
~ bad
~
y good ~ N(300;150) и y ~ N(450;150)
0.0025
Ygood
Ybad
0.0020
0.0015
0.0010
0.0005
200
400
600
800
1000
12

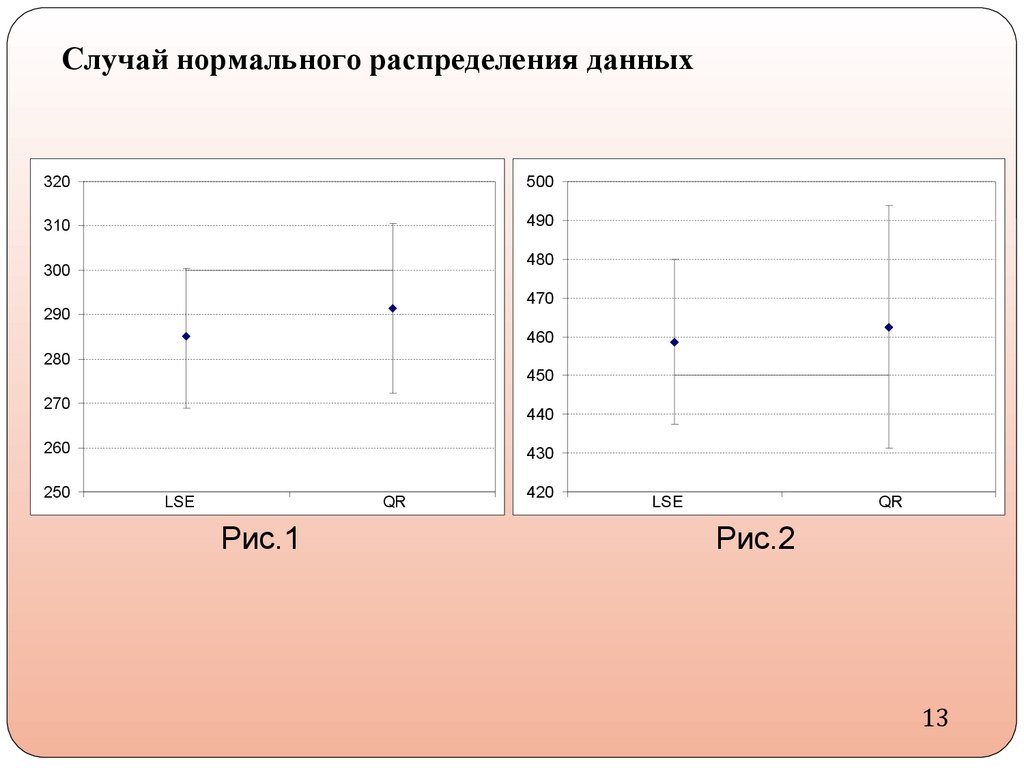
12.

Случай нормального распределения данных
320
500
310
490
480
300
470
290
460
280
450
270
440
260
250
430
LSE
QR
Рис.1
420
LSE
QR
Рис.2
13

13.

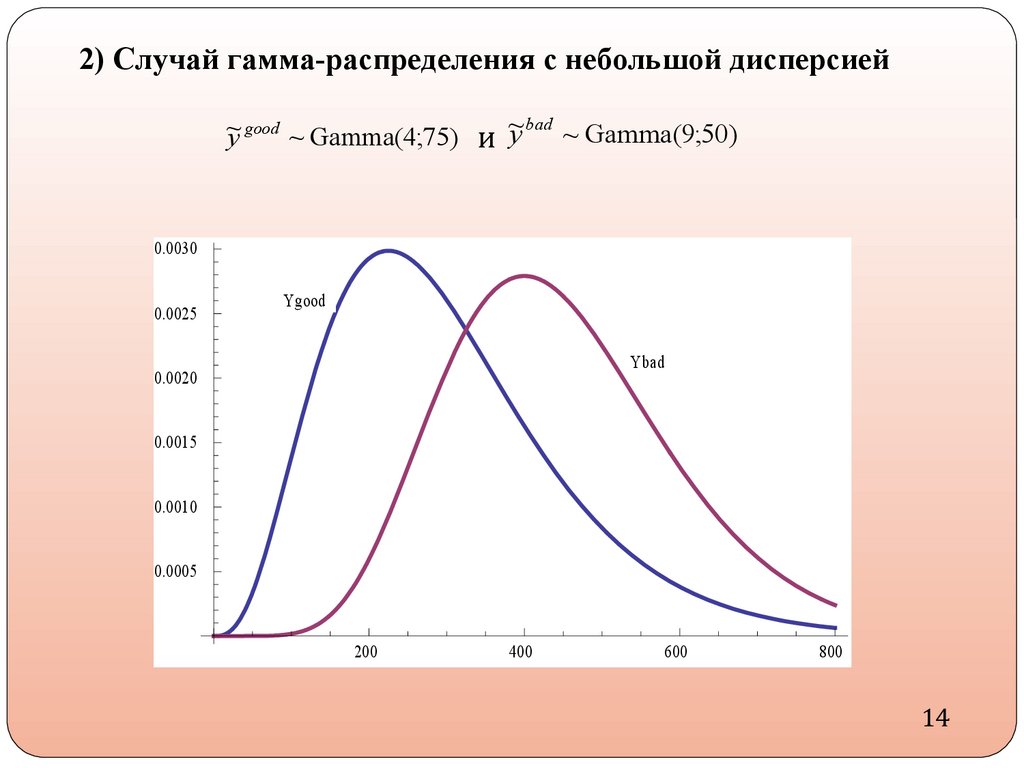
2) Случай гамма-распределения с небольшой дисперсией
~ bad ~ Gamma(9;50)
~
y good ~ Gamma(4;75) и y
0.0030
0.0025
Ygood
Ybad
0.0020
0.0015
0.0010
0.0005
200
400
600
800
14

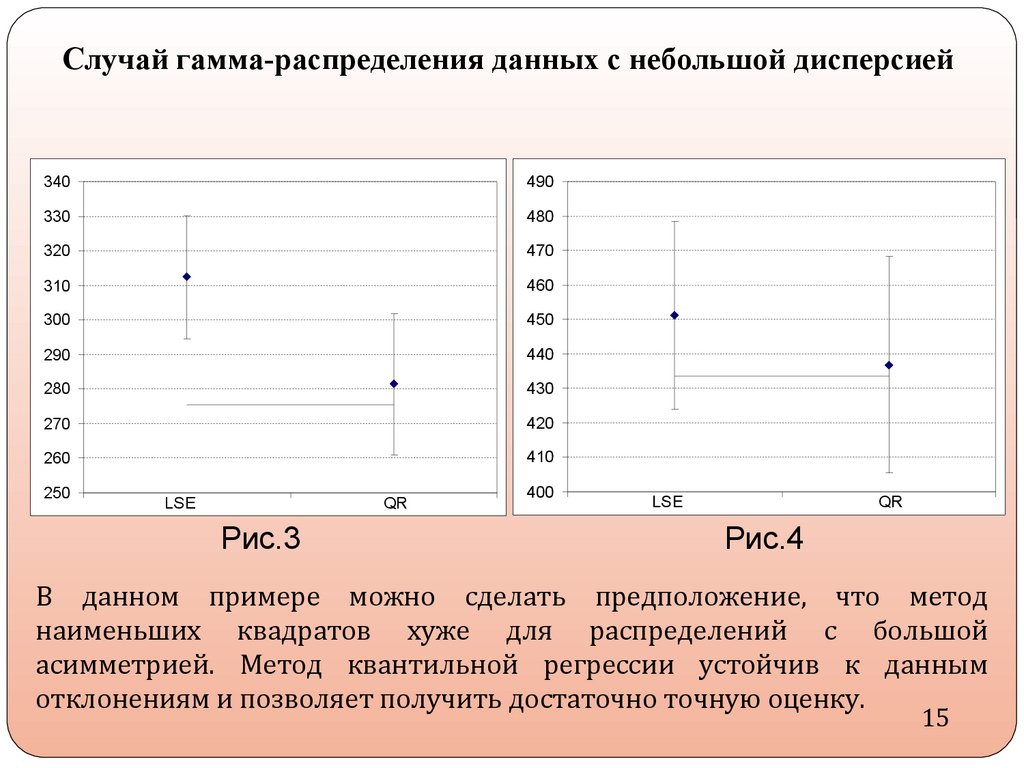
14.

Случай гамма-распределения данных с небольшой дисперсией
340
490
330
480
320
470
310
460
300
450
290
440
280
430
270
420
260
410
250
LSE
QR
Рис.3
400
LSE
QR
Рис.4
В данном примере можно сделать предположение, что метод
наименьших квадратов хуже для распределений с большой
асимметрией . Метод квантильной регрессии устой чив к данным
отклонениям и позволяет получить достаточно точную оценку.
15

15.

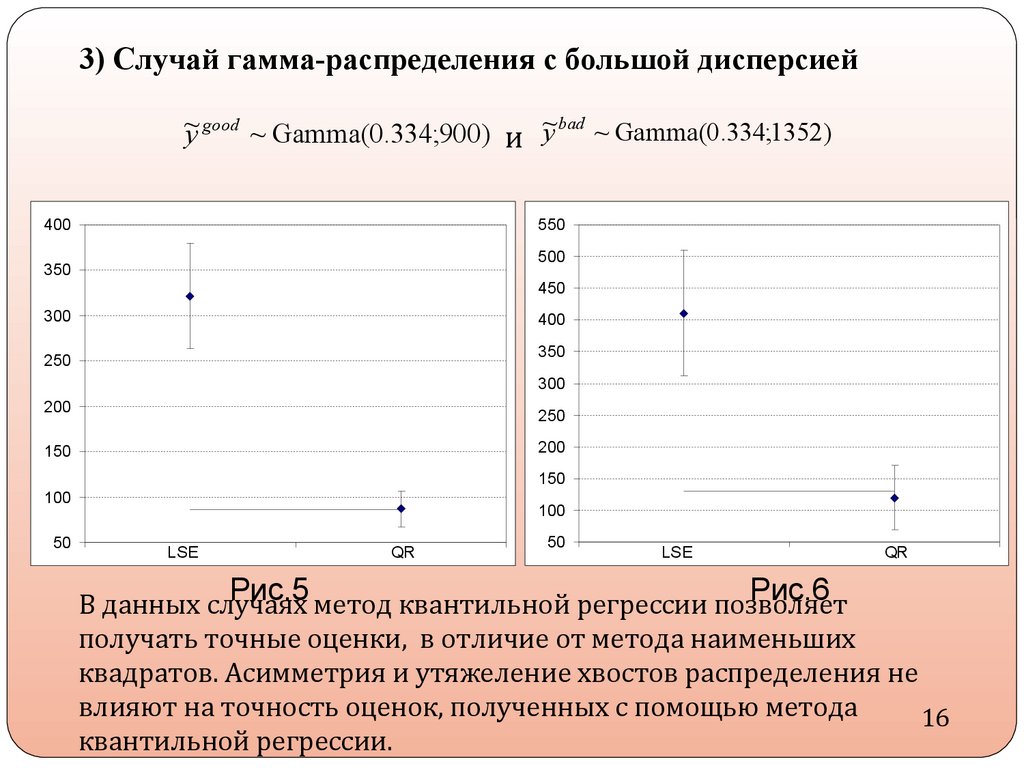
3) Случай гамма-распределения с большой дисперсией
~
y good ~ Gamma(0.334;900) и ~y bad ~ Gamma(0.334;1352)
550
400
500
350
450
300
400
350
250
300
200
250
200
150
150
100
50
100
LSE
QR
50
LSE
QR
Рис.5 метод квантильной регрессии позволяет
Рис.6
В данных случаях
получать точные оценки, в отличие от метода наименьших
квадратов. Асимметрия и утяжеление хвостов распределения не
влияют на точность оценок, полученных с помощью метода
16
квантильной регрессии.

16.

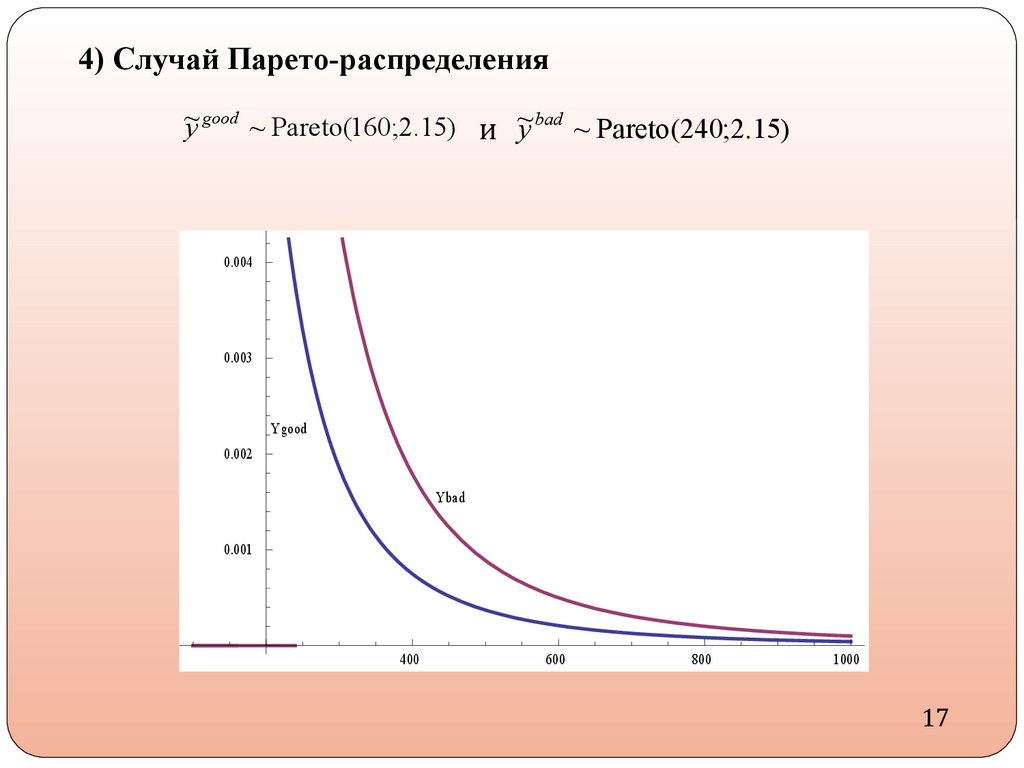
4) Случай Парето-распределения
~
y good ~ Pareto(160;2.15) и ~
y bad ~ Pareto(240;2.15)
0.004
0.003
Ygood
0.002
Ybad
0.001
400
600
800
1000
17

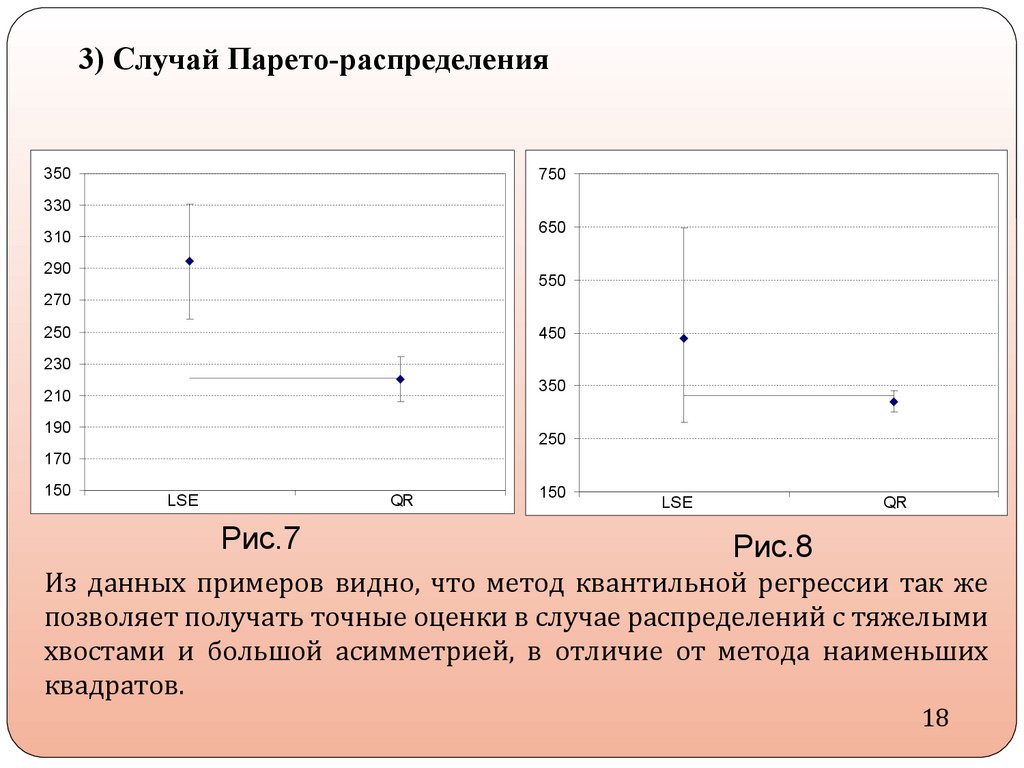
17.

3) Случай Парето-распределения
350
750
330
650
310
290
550
270
250
450
230
350
210
190
250
170
150
LSE
QR
Рис.7
150
LSE
QR
Рис.8
Из данных примеров видно, что метод квантильной регрессии так же
позволяет получать точные оценки в случае распределений с тяжелыми
хвостами и большой асимметрией , в отличие от метода наименьших
квадратов.
18

18.

Выводы:
1) Метод квантильной регрессии немного хуже метода
наименьших квадратов для нормального распределения
данных.
2) Для распределений с небольшой асимметрией метод
квантильной регрессии, как и метод наименьших
квадратов позволяет получать достаточно точные
оценки. Преимущество первого – свобода от от
предположения относительно закона распределения
исследуемых данных
3) Метод наименьших квадратов очевидно хуже для
распределений с большой асимметрией и распределений с
тяжелыми хвостами. Метод квантильной регрессии
преодолевает данные недостатки и позволяет получать
точные оценки
19

19.

Заключение
Основные результаты:
1) Рассмотрены принципы и методология бутстрап-метода:
- Приближение симуляциями
- Рецентрирование
- Корректировка смещения
- Инференция
- Асимптотическое рафинирование
2) Проведены модельные эксперименты – при помощи имитационного анализа и бутстрапметода исследованы оценки, полученные методом наименьших квадратов и методом
квантильной регрессии. Построены соответствующие доверительные интервалы.
3) Написан скрипт на языке программирования R, реализующий бутстрап-метод для построения
доверительных интервалов
4) На основании проведенных экспериментов сформулированы выводы о возможности
использования модели квантильной регрессии при различных условиях. Дальнейшие
исследования могут быть направлены на практическую апробацию данного метода в рамках
экономических задач.
20

20. Заключение

Спасибо за внимание