Первообразная

1.

ПЕРВООБРАЗНАЯ

2.

ОПРЕДЕЛЕНИЕ ПЕРВООБРАЗНОЙ
Определение. Функцию F(x) называют первообразной
для функции f(x) на заданном промежутке X, если для
всех x из выполняется равенство:
F`(x) = f(x)

3.

РАЗЪЯСНЕНИЯ
• Дана функция F(x). Найти F`(x).
Процесс называется дифференцированием.
• Обратная задача: Дана функция f(x) – производная
неизвестной функции F(x). Найти F(x) –
первообразную.
Процесс называется интегрированием.

4.

ТАБЛИЦА ПЕРВООБРАЗНЫХ

5.

ПРИМЕР
f (x) = 3x2
• (xn) = nxn-1 и применим к нашей задаче (x3) = 3x2
- F (x) = x3
• Однако производная от константы C = 0, тогда:
- (x3 + 2) = 3x2
- (x3 + 6) = 3x2
- (x3 + C) = 3x2

6.

ОСНОВНОЕ СВОЙСТВО
ПЕРВООБРАЗНЫХ
Если функция F(x) — первообразная функции f(x)
на заданном промежутке, то, при любой
постоянной С=const, функция F(x)+С также
является первообразной функции f(x) на этом
промежутке

7.

ГРАФИЧЕСКИЙ ПРИМЕР

8.

ГРАФИЧЕСКИЙ ПРИМЕР

9.

ПРАВИЛА НАХОЖДЕНИЯ
ПЕРВООБРАЗНЫХ

10.

ПОНЯТИЕ ИНТЕГРАЛА
Интеграл – это сумма всех первообразных
функции

11.

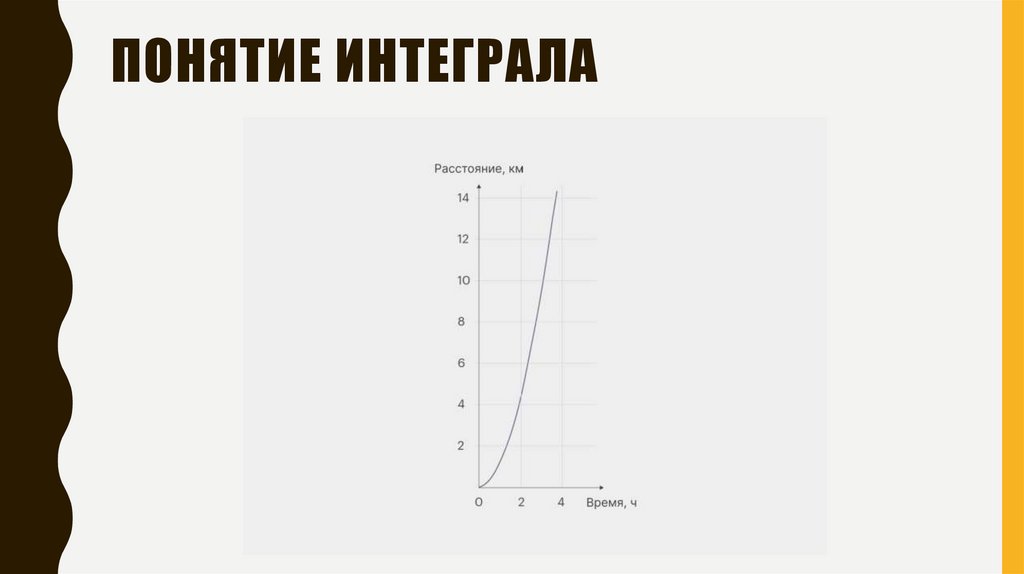
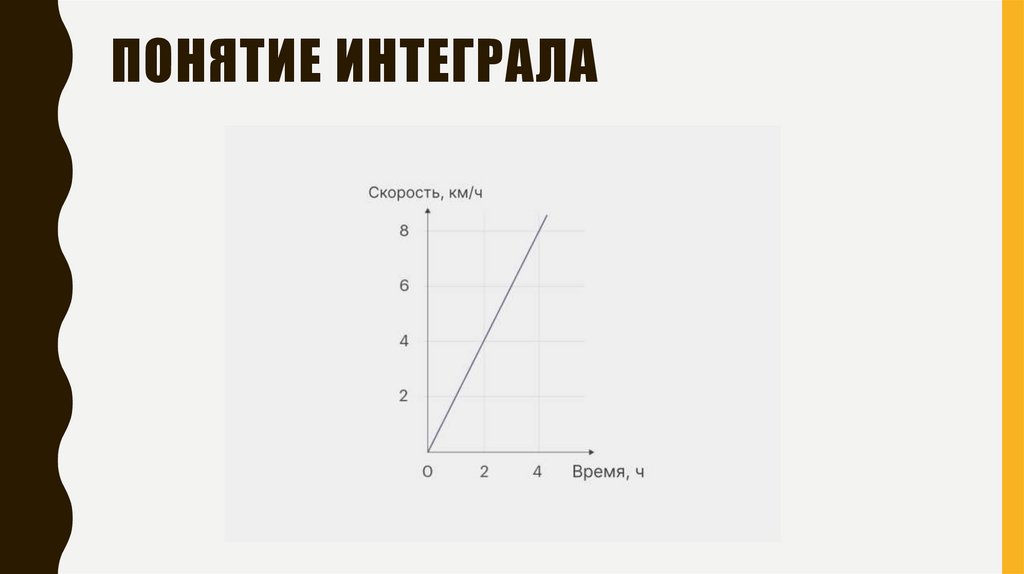
ПОНЯТИЕ ИНТЕГРАЛА

12.

ПОНЯТИЕ ИНТЕГРАЛА

13.

ПОНЯТИЕ ИНТЕГРАЛА

14.

ПОНЯТИЕ ИНТЕГРАЛА

15.

ПОНЯТИЕ ИНТЕГРАЛА

16.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределённый интеграл — это интеграл, для
которого не задан промежуток интегрирования.

17.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

18.

СВОЙСТВА НЕОПРЕДЕЛЁННОГО
ИНТЕГРАЛА

19.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
• 1. Метод вычисления интегралов с помощью таблицы
интегралов и правил интегрирования

20.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

21.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
• 2. Метод подведения под знак дифференциала (dx)
• Свойства дифференциалов:
d(f(x)) = f`(x)dx
d(f(x) + C) = d(f(x))
d(C*f(x)) = C*d(f(x))

22.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

23.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
• 3. Метод интегрирования по частям
• Если u = u(x) и v = v(x) - дифференцируемые функции,
то справедлива формула интегрирования по частям:

24.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

25.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
• 4. Метод замены переменной (метод подстановки)
• Пусть функция x = ф(t) непрерывно
дифференцируемая на некотором промежутке и имеет
обратную функцию t = w(x).
Тогда ʃ(f(x)*dx) = ʃ(f(ф(t))* ф`(t)*dt)

26.

МЕТОДЫ ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

27.

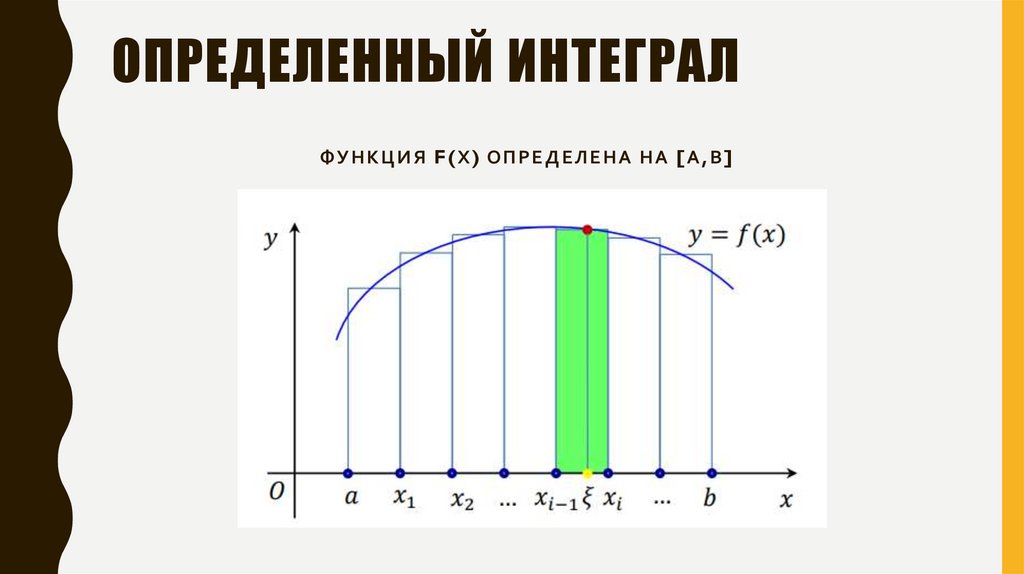
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ФУНКЦИЯ F(X) ОПРЕДЕЛЕНА НА [A,B]

28.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
РА С С М ОТ Р И М РА З Б И Е Н И Е ОТ Р Е З К А [ A , B ] Н А N ОТ Р Е З КО В ТО Ч К А М И

29.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегральной суммой для функции y=f(x) на отрезке
[a,b] называется сумма произведений длин
элементарных отрезков ∆xi на значения функции f(ξi) в
произвольных точках этих отрезков

30.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенным интегралом функции f (x) на [a,b] называется
число при условии, что предел интегральных сумм существует и
не зависит от способа разбиения на элементарные отрезки и от
выбора фиксированной точки ξ i ( a – нижний предел, b –
верхний предел определенного интеграла).

31.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определённым интегралом от функции на отрезке называют
предел соответствующих интегральных сумм и обозначают:

32.

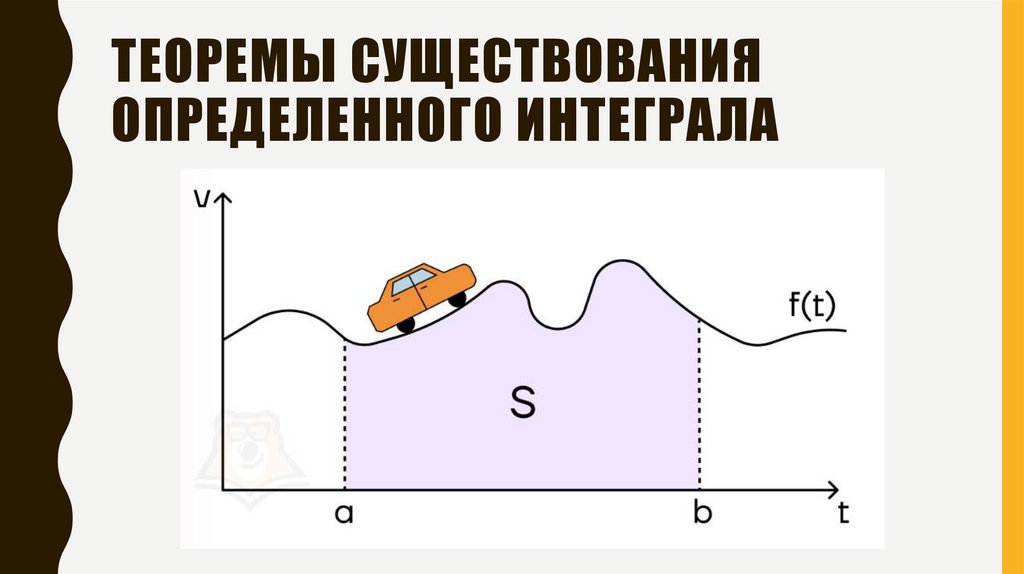
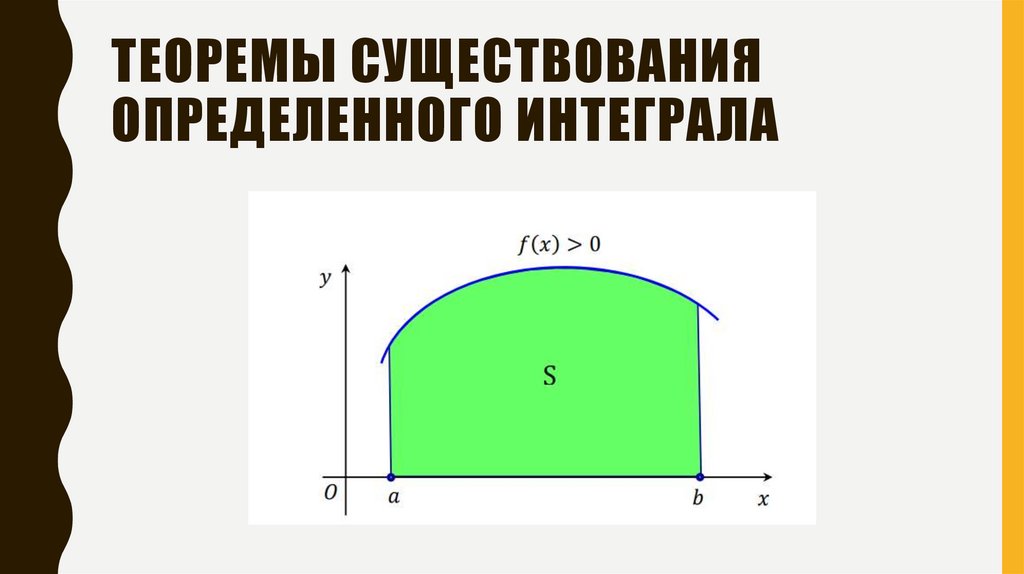
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

33.

ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

34.

ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

35.

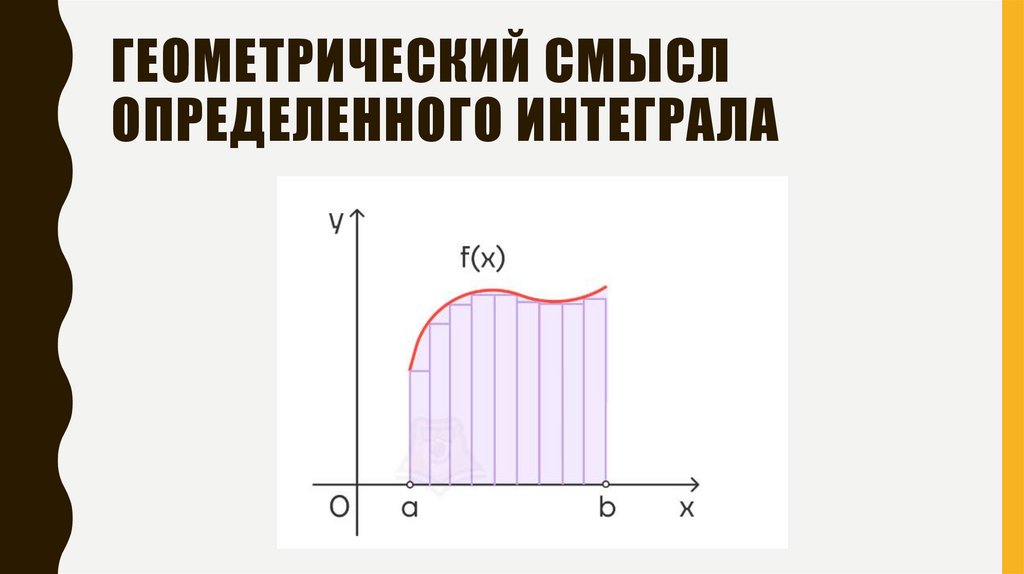
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Геометрический смысл: определённый интеграл численно
равен площади криволинейной трапеции.

36.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

37.

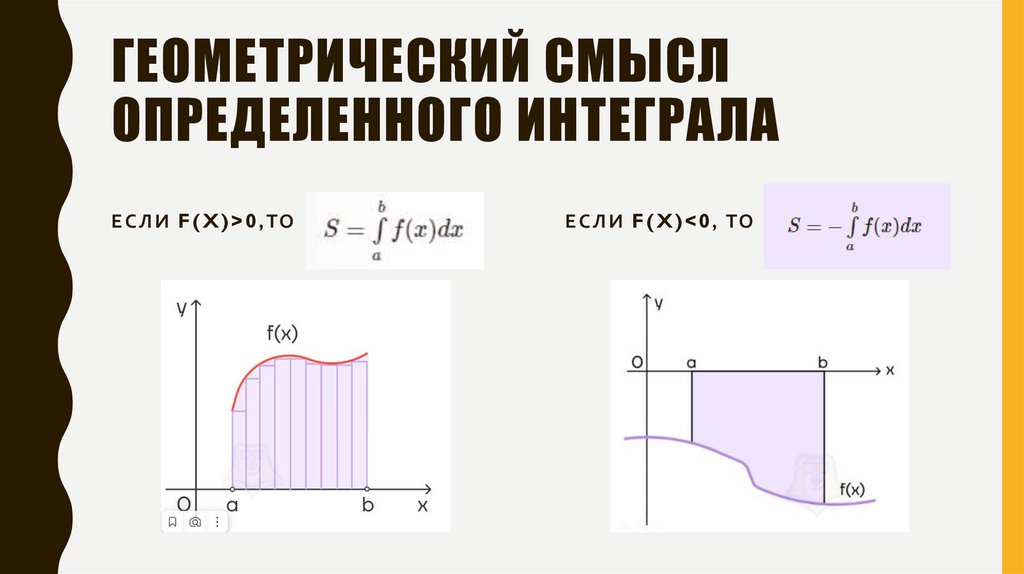
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Е С Л И F ( X ) > 0 , ТО
Е С Л И F ( X ) < 0 , ТО

38.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА

39.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Формула Ньютона-Лейбница для вычисления определённого
интеграла:

40.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Алгоритм вычисления определённого интеграла:
1. Найдите первообразную F(x), то есть неопределённый
интеграл (константу C не добавляйте).
2. Подставьте b в первообразную, найдите F(b).
3. Подставьте a в первообразную, найдите F(a).
4. Найдите разность F(b) − F(a).

41.

СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА

42.

ПРИМЕР РЕШЕНИЯ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА

43.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 1. Производная интеграла по верхнему пределу.
• 2. Формула Ньютона – Лейбница.
• 3. Замена переменной в определенном интеграле.
• 4. Интегрирование по частям.

44.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 1. Производная интеграла по верхнему пределу.
Рассмотрим функцию f (x) , интегрируемую на [a,b].
Пусть x – произвольная точка отрезка [a,b].
Функция F(x) называется интегралом с переменным
верхним пределом.

45.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 1. Производная интеграла по верхнему пределу.
Если f (x) непрерывна на [a,b], то:

46.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 1. Производная интеграла по верхнему пределу.
Следствие (теорема Коши):
- Всякая непрерывная на [a,b] функция f (x) имеет в этой
области первообразную

47.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 2. Формула Ньютона – Лейбница
Если f (x) непрерывна на [a,b], то:

48.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 3. Замена переменной в определенном интеграле
1) Если f (x) непрерывна на [a,b] ;
2) x = g(t), x` = g`(t) непрерывны на [ą, ß];
3) a = g(ą), b = g(ß), то:

49.

МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
• 4. Интегрирование по частям
• Если u(x) и v(x) имеют на [a,b] непрерывные
производные, то:

50.

ТЕСТ