Теорема Кориолиса о сложении ускорений

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 9.
Теорема Кориолиса о сложении ускорений.
По аналогии с §8.2. определим ускорение точки.
§9.1. Теорема Кориолиса о сложении ускорений.
Абсолютное ускорение точки геометрически
складывается из 3-х компонент: относительного
ускорения, переносного ускорения и ускорения
Кориолиса (поворотного ускорения).
a aa ar a e ak
(56)

3.

Возьмем за основу db d r b
.Тогда
b
dt
dt
dVa dVr dVe d r Vr
d eVr
aa a
e Vr a r e Vr a r
dt
dt
dt
dt
dt
dt
det dV
dVr d rV d eVr
ar e Vr
dt
dt
dt
(57)
det
dVe d Vc e r
dr dVe
a c w r E
a c e r
dt
dt
dt dt
e e r e Vr
u вр
цс
ae ac a M C a M C
(58)

4.

Так как по определению
переносное ускорение точки есть ускорение той
точки М´ подвижного пространства (или твердого
тела, связанного с подвижными осями) по
отношению к неподвижным осям, через которую в
данный момент времени проходит движущаяся
точка М.
dVe M
a e a e ae e Vr
dt
То:
det
'
вр
цс
M
Где,
ae ae ac a M / C a M / C
(59)

5.

Таким образом
d rVr deVe deVr d rVe
a aa ar ae ak
dt
dt
dt
dt
(60)

6.

§9.2.Ускорение Кориолиса.
Поворотное ускорение или ускорение Кориолиса
возникает только при наличии вращения подвижных
осей и характеризует быстроту изменения
относительной скорости в переносном движении и
быстроту изменения переносной скорости в
относительном движении, и состоит из 2-х равных
поворотных компонент
d eVr d rVe
ak
2 e Vr
dt
dt
(61)

7.

Определим, при каких условиях ускорение Кориолиса
обращается в ноль. Это имеет место при
ak 0
1) e 0 t
2) V r 0 в t
e V r
3) sin e , V r 0
e V r
Возникает вопрос о том, как можно подсчитать его
алгебраическую величину, компоненты и определить
направление?

8.

1) Алгебраическая величина
ak 2 e V r sin 0
2) Компоненты в декартовых координатах
i
ak 2 ex
Vrx
j
ey
Vry
k
ez i eyVrz ezVry j ezVrx exVrz k exVry eyVrx
Vrz
akx 2 eyVrz ezVry
aky 2 ezVrx exVrz
akz 2 exVry eyVrx
(62)

9.

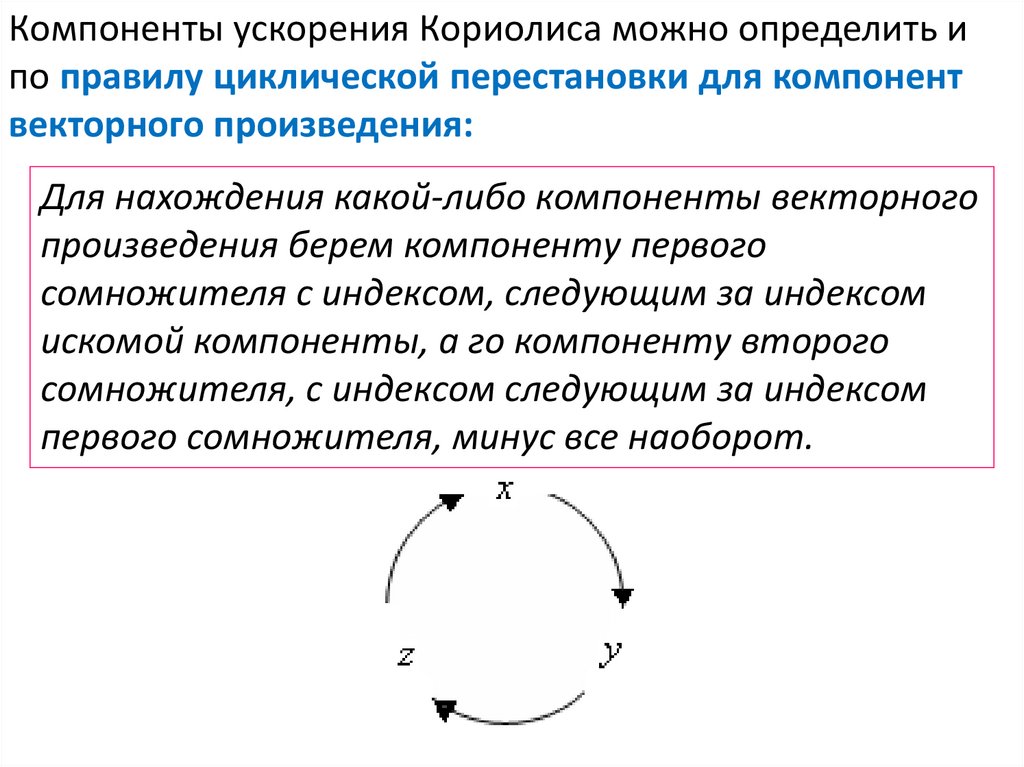
Компоненты ускорения Кориолиса можно определить и
по правилу циклической перестановки для компонент
векторного произведения:
Для нахождения какой-либо компоненты векторного
произведения берем компоненту первого
сомножителя с индексом, следующим за индексом
искомой компоненты, а го компоненту второго
сомножителя, с индексом следующим за индексом
первого сомножителя, минус все наоборот.

10.

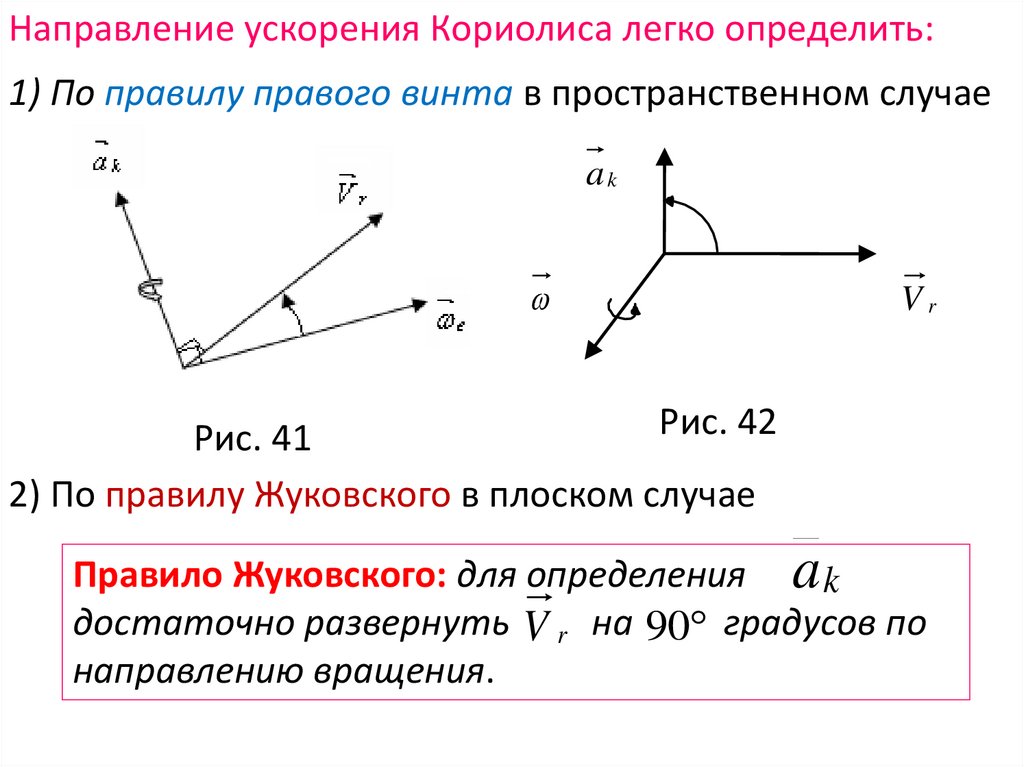
Направление ускорения Кориолиса легко определить:
1) По правилу правого винта в пространственном случае
ak
Vr
Рис. 42
Рис. 41
2) По правилу Жуковского в плоском случае
Правило Жуковского: для определения a k
достаточно развернуть V r на 90 градусов по
направлению вращения.

11.

§9.3.
Пример
типа
К-7.
Определить V , a точки М в момент t=1c
ak
t
ar , Vr
Вычислим скорость точки.
S r / t 1 5 (см)
e / t 1 4( рад / c)
вр
aе a n
r
,
цс
aе
e / t 1 2( рад / c )
2
Согласно теореме о сложении скоростей
(рис. 44)
V Vr V e
Рис. 43

12.

2
100 2
10 2 ...(см / c 2 )
МС
10
Vr2
100
n
ar t 1c ( ) t 1c
*
Vr S r 10 t (см / c)
Vr / t 1c 10 t 31.42(см / c) 0
Ve / t 1c ( e cм ) / t 1c ( e cм) / t 1c e / t 1c 2r 4 1.41 10 56.40(cм / c)
Вычислим модуль скорости точки М.
2
2
2
V (V r V e ) Vr 2(V r V e ) Ve2
V t 1 Vr2 2(V r V e ) ve2
Вычислим ускорение точки
t n
вр ц.с.
a a r a e a k (a r ar ) (a e a c ) a k
a r V r 10 (см / c 2 ) t
ak
aеврa n
r
t
ar , Vr
,
цс
aе

13.

2
100 2
10 2 ...(см / c 2 )
МС
10
Vr2
100
n
ar t 1c ( ) t 1c
acвр t 1с ( e см) t 1с … (см / c 2 )
acц.с. t 1с ( 2 e см) t 1с ...
ak t 1c 2( eVr )t 1c ...(см / c 2 )
Для определения модуля ускорения воспользуемся
методом проекций, как и в К-3. Дорешаем задачу в
качестве упражнения дома.