Расстояние между двумя точками

1.

Однажды Сократ, окружённый учениками,
поднимался к храму. Навстречу им спускалась
известная афинская гетера.
“Вот ты гордишься своими учениками, Сократ, улыбнулась она ему, - но стоит мне только
легонько поманить их, как они покинут тебя и
пойдут вслед за мной”.
Мудрец же ответил так:
“Да, но ты зовёшь их вниз, в тёплую весёлую
долину, а я веду их вверх, к неприступным,
чистым вершинам”.Вот и мы с вами сегодня
должны подняться на одну ступеньку вверх,
“преодолевая” задачи, которые будут
рассмотрены на сегодняшнем уроке, тема
которого …

2.

Тема урока:
РАССТОЯНИЕ
МЕЖДУ
ДВУМЯ ТОЧКАМИ

3.

-записывать формулу расстояния между
двумя точками в пространстве;
-применять формулу расстояния между
двумя точками в пространстве при
решении задач.

4.

Расстояние между точками на плоскости;
Деление отрезка пополам на плоскости;
Определение координат точки в
прямоугольной системе координат в
пространстве
Определение координат вектора по
координатам начала и конца вектора

5.

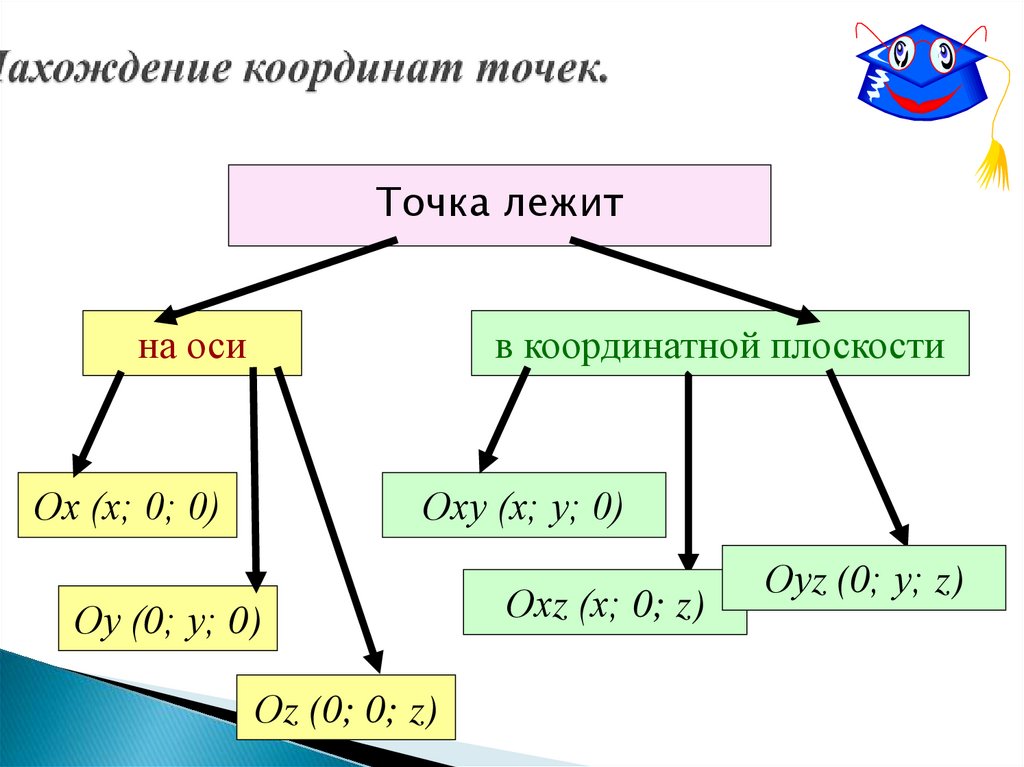
Точка лежит
на оси
в координатной плоскости
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)

6.

7.

8.

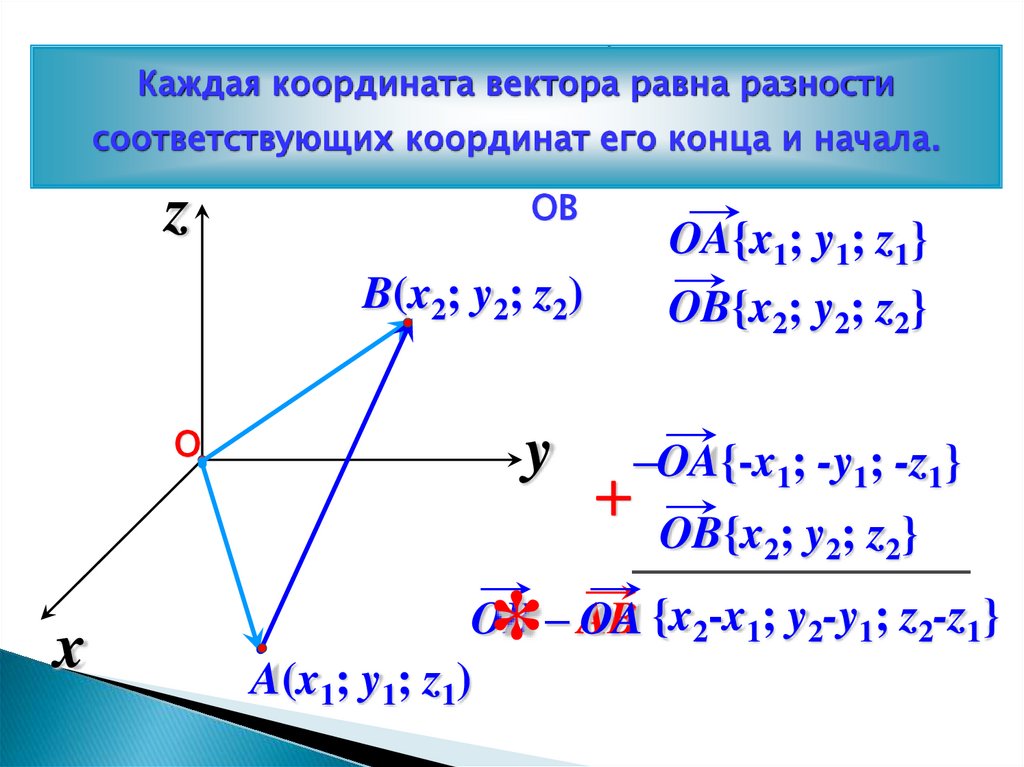
Выразим
через
Каждаякоординаты
координатавектора
вектораАВ
равна
разности
координаты
соответствующих координат его конца и начала.
его начала А
Изи конца
АОB, В.
AB = AО +
= –ОA + ОB
ОB
z
OA{x1; y1; z1}
OB{x2; y2; z2}
B(x2; y2; z2)
О
x
y
*
–OA{-x1; -y1; -z1}
+
OB{x2; y2; z2}
OB – AB
OA {x2-x1; y2-y1; z2-z1}
A(x1; y1; z1)

9.

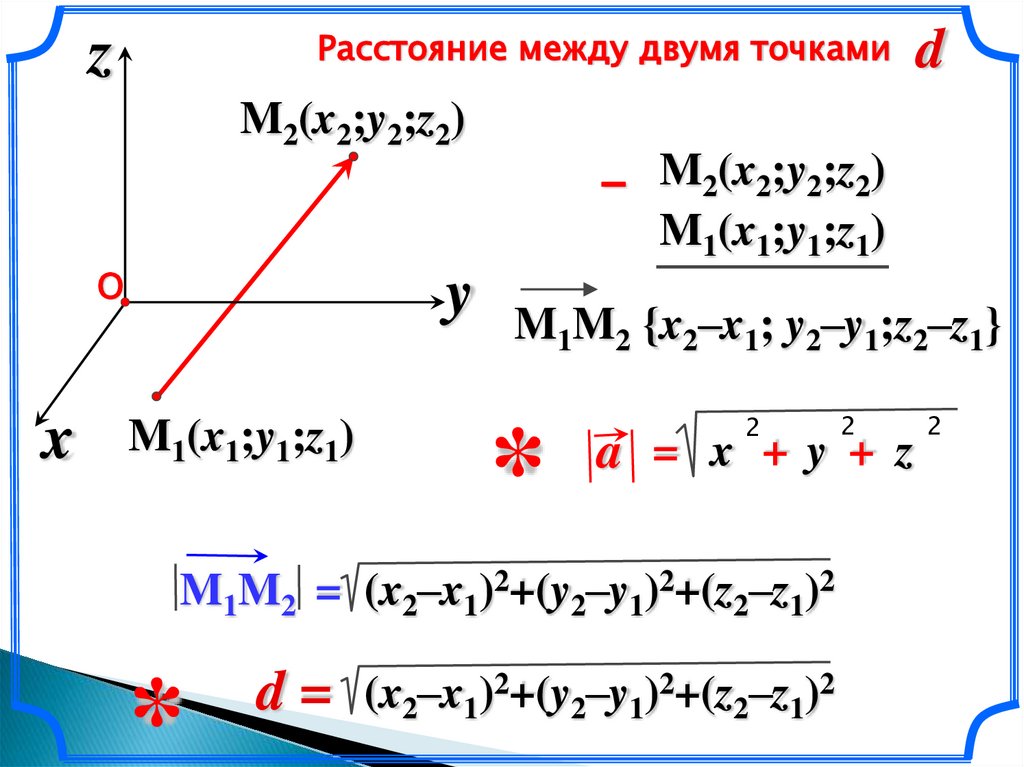
Расстояние между двумя точками
z
M2(x2;y2;z2)
– M2(x2;y2;z2)
M1(x1;y1;z1)
О
y M M {x –x ; y –y ;z –z }
1
x
d
M1(x1;y1;z1)
*
2
2
1
2
2
2
2
a = x +y + z
M1M2 = (x2–x1)2+(y2–y1)2+(z2–z1)2
*
1
d = (x2–x1)2+(y2–y1)2+(z2–z1)2
2
1

10.

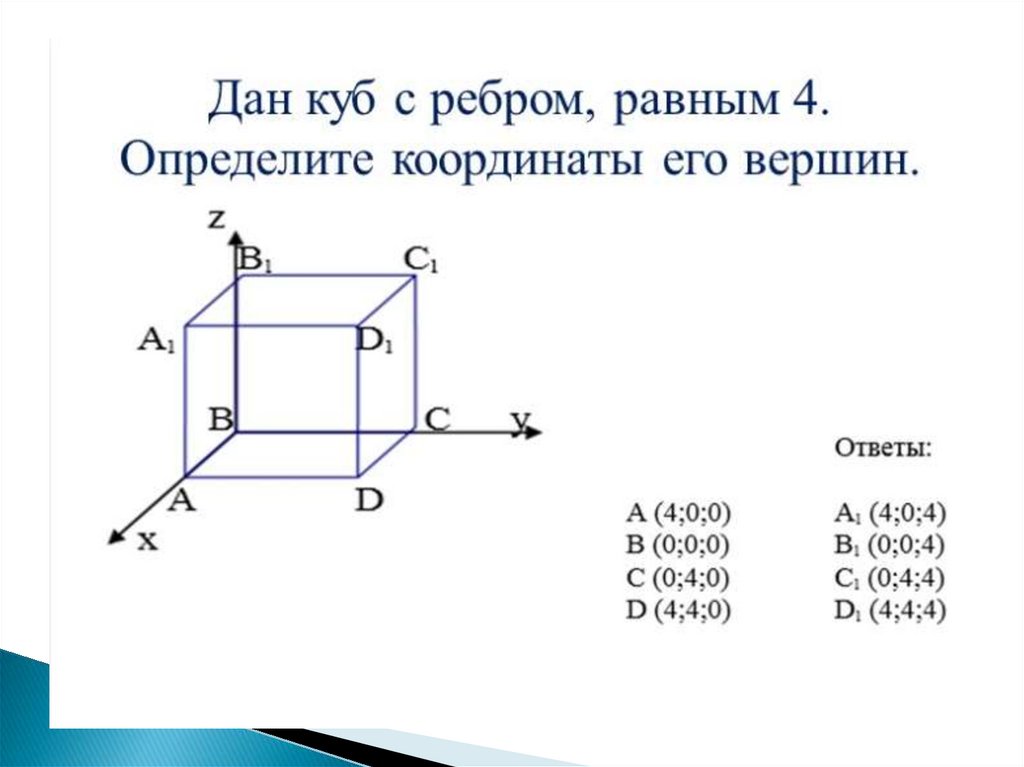
1. Даны точки А и В. Найти координаты середины отрезка АВ
а) Найдите координаты середины отрезка АВ.