Похожие презентации:
Расстояние между двумя точками в пространстве (10 класс)
1.
Раздел: Прямоугольная системакоординат и векторы в пространстве
Тема урока:
Расстояние между двумя точками в
пространстве
2.
Цель обучения10.4.2
уметь находить расстояние между
двумя точками в пространстве
3.
Критерии успеха:Учащийся
записывает формулу расстояния между
двумя точками в пространстве;
применяет формулу расстояния между
двумя точками в пространстве при
решении задач.
4.
Повторение:1. Даны точки А ( - 1; 7 ) и В ( 7; 1).
а) Найдите координаты середины отрезка АВ.
у А уВ
х А хВ
уС
хС
2
2 С ( 3; 4)
б) Найдите длину отрезка АВ.
АВ
х х у у
2
В
А
2
В
А
|АВ| = 10
5.
Повторение:2. Запишите координаты вектора
т 3;2
т 3i 2 j
3. Среди векторов
а 4;5 ; b 8;10 ; c 2; 2,5
укажите пару коллинеарных векторов.
Ненулевые векторы наз. коллинеарными, если они
лежат либо на одной прямой, либо на параллельных
прямых
?
a kb
а
k<0
b
а и b; b 2a
b
а
k>0
6.
Повторение:4. Найдите координаты вектора EF, если
Е ( -2; 3), F ( 1; 2).
EF x F x E ; y F y E
EF 3; 1
5. Найдите расстояние между точками
А (а; 0) и В (b; 0).
АВ
АВ b a
х х у у
2
В
А
2
В
А
7.
Задание прямоугольной системыкоординат в пространстве:
z
1
Ох – ось абсцисс
Оу – ось ординат
Оz – ось аппликат
A
1
О
1
A (1; 1; 1)
x
y
Оy Оz
Оz Оx
Оy Оx
8.
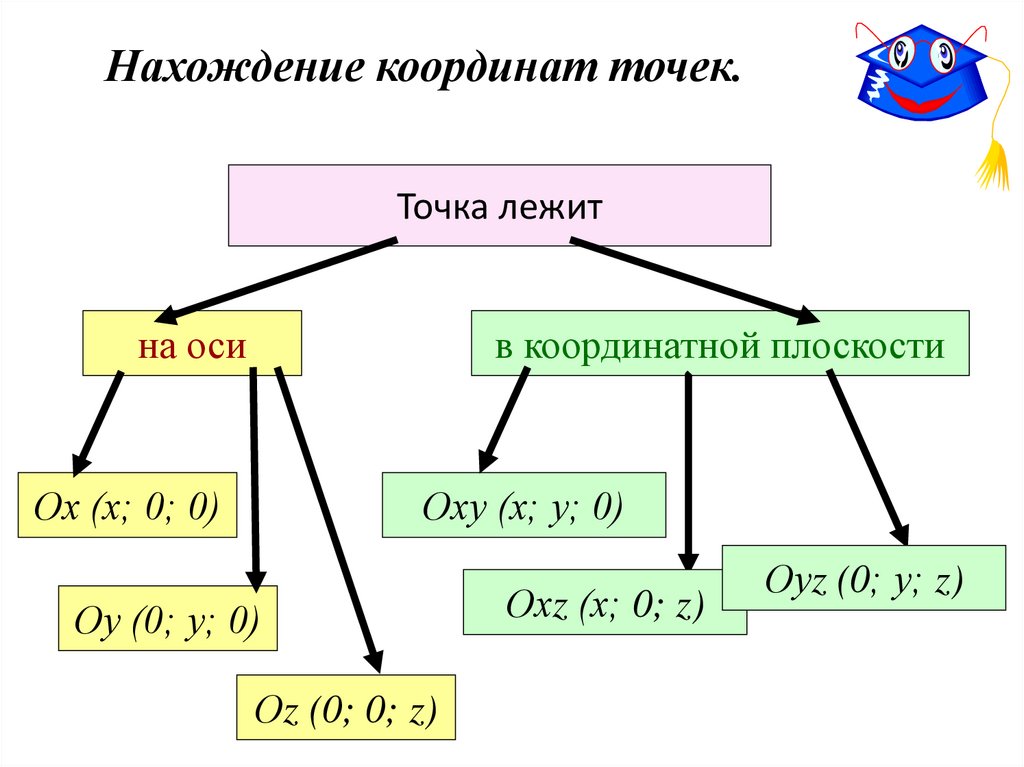
Нахождение координат точек.Точка лежит
на оси
в координатной плоскости
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)
9.
Решение задач.Рассмотрим точку А (2; -3; 5)
1) A4 : Ox
A4 (2; 0; 0)
A6
2
z
A
2) A5 : Oу
5
A5 (0; -3; 0)
3) A6 : Oz
A6 (0; 0; 5)
A5
0
-3
хA4
у
10.
zНайти координаты точек А, В, С и
В
I
I
I
I
I
I
O I
I
B(-2;-3; 4)
OB{-2;-3; 4}
I
j
I
I
I
x
I
I
I
I
I
i
OA{-1; 3;-6}
I
I
k
A(-1; 3;-6)
I
I
I
I
I
С
I
I
векторов ОА, ОВ, ОС
А
y
C( 3;-2; 6)
OC{ 3;-2; 6}
11.
Выразимкоординаты
вектора
АВ через
координаты
Каждая
координата
вектора
равна
разности
его начала А и конца В.
соответствующих координат его конца и начала.
Из АОB,
AB = AО + ОB = –ОA + ОB
z
B(x2; y2; z2)
О
x
y
*
OA{x1; y1; z1}
OB{x2; y2; z2}
–OA{-x1; -y1; -z1}
+ OB{x ; y ; z }
2
2 2
OB – AB
OA {x2-x1; y2-y1; z2-z1}
A(x1; y1; z1)
12.
A(3;5;7), B (5;4;-1), ABA(3;5;7)
–
B(5;4;-1)
AB{2;-1;-8}
N(3;2;-3), O(0;0;0), ON Радиус-вектор ON{3; 2;-3}
P(2;-1;0)
–
P (2;-1;0), C (4;-4;2), PC
C(4;-4;2)
R(-4;0;-4), T (0;5;-1), TR
D(-3;-4;0), O(0;0;0), OD
Радиус-вектор
OD{-3;-4; 0}
PC{2;-3; 2}
R(-4;0;-4)
–
T(0; 5;-1)
TR{-4;-5;-3}
13.
Вычисление длины вектора по его координатамz
a {x;y;z}
По правилу параллелепипеда
2= 2OA
2+
2 +OA
22+
22
OAOA
= OA
OA
+
OA
1 1
22
3
A3
OA1 = xi = x
A
zk a
О
xi
OA2 = y j = y
yj
A2
2
A1
x
y
OA3 = zk = z
2
2
2
2
2
a = x + y + z
*
a = x +y + z
2
14.
zd
Расстояние между двумя точками
M2(x2;y2;z2)
M
(x
;y
;z
)
2
2
2
2
–
M1(x1;y1;z1)
y M M {x –x ; y –y ;z –z }
О
1
x
M1(x1;y1;z1)
*
2
2
1
2
2
2
2
a = x +y + z
M1M2 = (x2–x1)2+(y2–y1)2+(z2–z1)2
*
1
d = (x2–x1)2+(y2–y1)2+(z2–z1)2
2
1
15.
Найдите длину вектора АВA(-1;0;2) и B(1;-2;3)
1 способ
1)
a = x 2 + y 2 + z2
B(1;-2;3)
–
A(-1;0;2)
2)
AB = 22+(-2)2+12 = 9 = 3
AB{2;-2;1}
2 способ
AB = (x2–x1)2+(y2–y1)2+(z2–z1)2
AB = (1+1)2+(–2–0)2+(3–2)2














 Математика
Математика








