Методы проецирования. Свойства и особенности ортогонального проецирования

1. ИНЖЕНЕРНАЯ ГРАФИКА

Лектор
Милютина
Дина Геннадьевна

2.

http://graph.power.nstu.ru

3. ЛЕКЦИЯ №1

Цели дисциплины.
Методы проецирования.
Свойства и особенности ортогонального
проецирования.
Проецирование объектов на 1, 2 и 3
плоскости проекции.

4. ЦЕЛИ ДИСЦИПЛИНЫ

• Знать алгоритмы геометрического
моделирования геометрических объектов.
• Уметь использовать графический редактор
КОМПАС для создания чертежа детали.
• Знать требования стандартов единой
системы конструкторской документации.
• Уметь читать и разрабатывать
конструкторские документы.

5. Начертательная геометрия -

Начертательная геометрия наука, занимающаяся изучением
графических методов отображения
пространства на плоскости
Инженерная графика –
правила выполнения и оформления
конструкторской документации.
Прикладная компьютерная графика –
выполнение и редактирование чертежей с
помощью графических редакторов.

6.

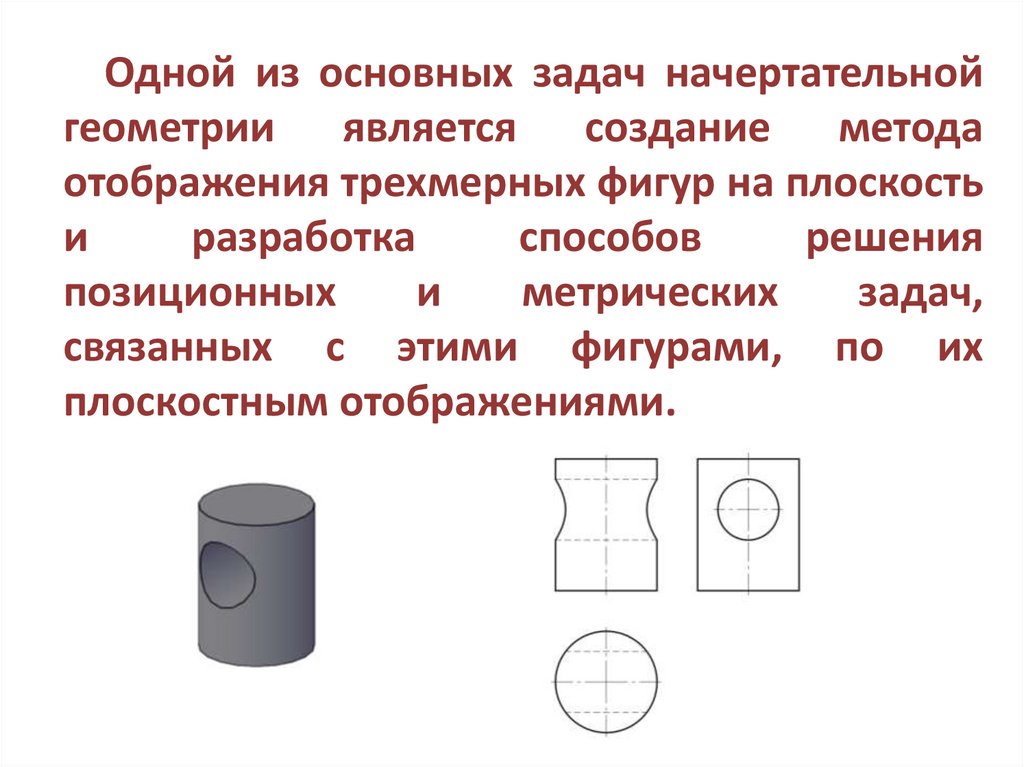
Одной из основных задач начертательной
геометрии является создание метода
отображения трехмерных фигур на плоскость
и
разработка
способов
решения
позиционных
и
метрических
задач,
связанных с этими фигурами, по их
плоскостным отображениями.

7. В начертательной геометрии изображения получают методом проецирования

(лат. Projicio – бросаю вперёд) – процесс
получения изображения предмета
(пространственного объекта) на какойлибо поверхности с помощью световых или
зрительных лучей (лучей, условно
соединяющих глаз наблюдателя с какойлибо точкой пространственного объекта),
которые называются проецирующими.

8.

В зависимости от положения центра
проецирования по отношению к
плоскости проекций проецирование
может быть или центральным, или
параллельным.

9.

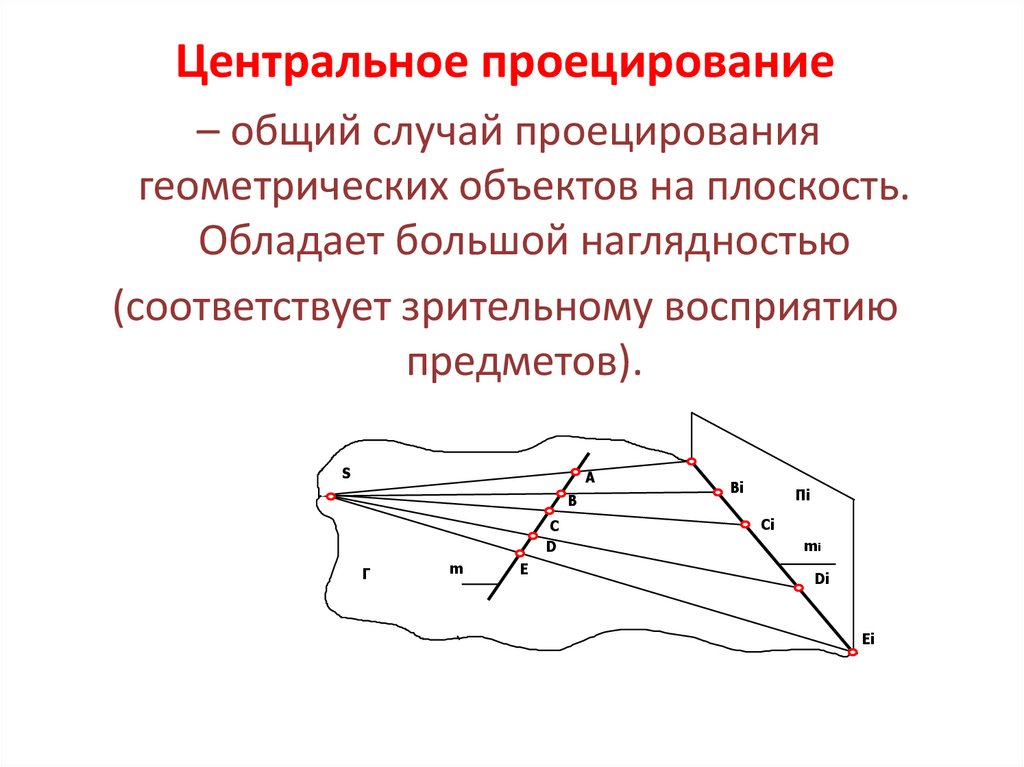
Центральное проецирование
– общий случай проецирования
геометрических объектов на плоскость.
Обладает большой наглядностью
(соответствует зрительному восприятию
предметов).
S
А
В
С
D
Г
m
Е
Bi
Пi
Ci
mi
Di
Ei

10.

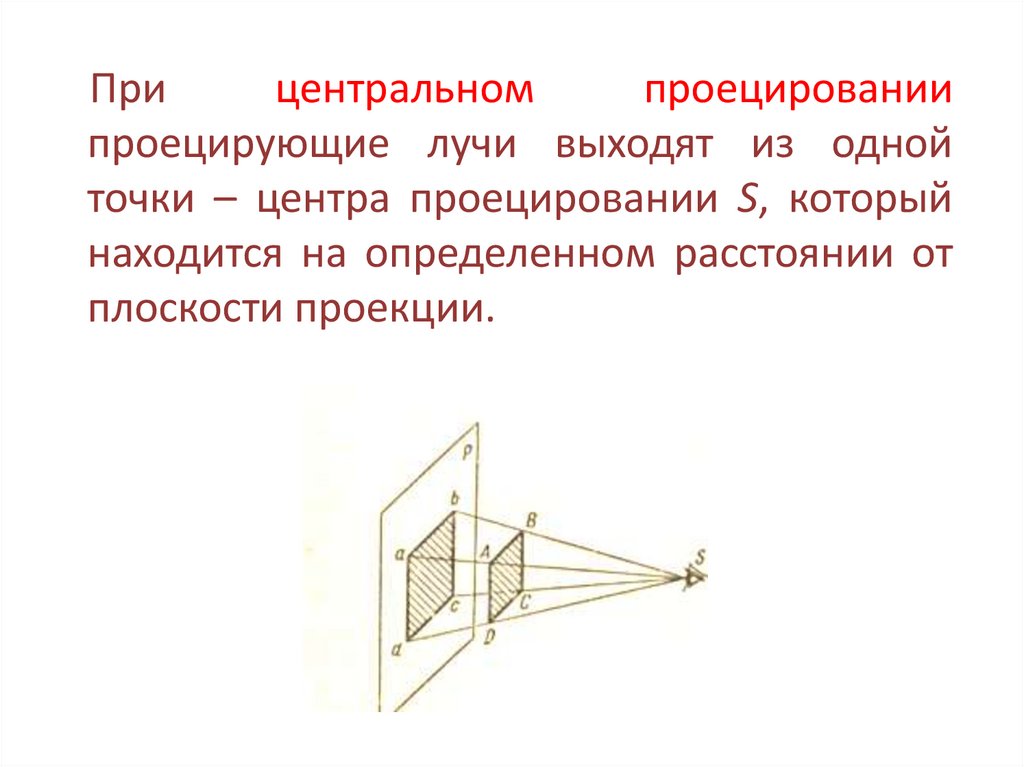
При
центральном
проецировании
проецирующие лучи выходят из одной
точки – центра проецировании S, который
находится на определенном расстоянии от
плоскости проекции.

11.

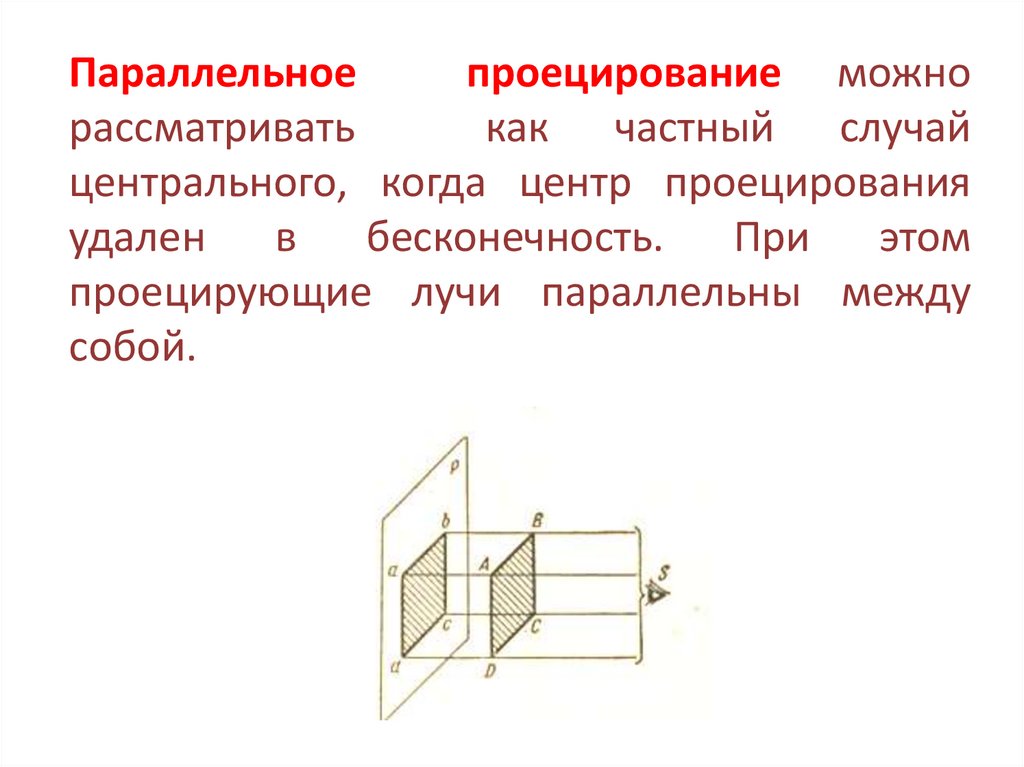
Параллельное
проецирование можно
рассматривать
как частный случай
центрального, когда центр проецирования
удален
в
бесконечность.
При
этом
проецирующие лучи параллельны между
собой.

12. Ортогональное проецирование

Это частный случай параллельного проецирования.
При ортогональном проецировании проецирующие
лучи перпендикулярны к плоскости проекций.
Чтобы получить ортогональную проекцию точки А,
через неё надо провести проецирующий луч
перпендикулярно к П1. Точка А1 называется
ортогональной или прямоугольной проекцией
точки А

13. Основные свойства параллельного проецирования

• проекции точки на плоскости есть точка;
• проекции прямой линии на плоскости есть прямая;
• если точка принадлежит линии, то проекция точки
принадлежит проекции этой линии;
• если отрезок прямой линии делится точкой в каком- либо
отношении, то и проекция отрезка делится проекцией
точки в том же отношении;
• плоская фигура, параллельная плоскости проекций,
проецируется на эту плоскость без искажения;
• прямой угол проецируется без искажения, если одна из его
сторон параллельна плоскости проекции, а другая не
перпендикулярна ей.

14.

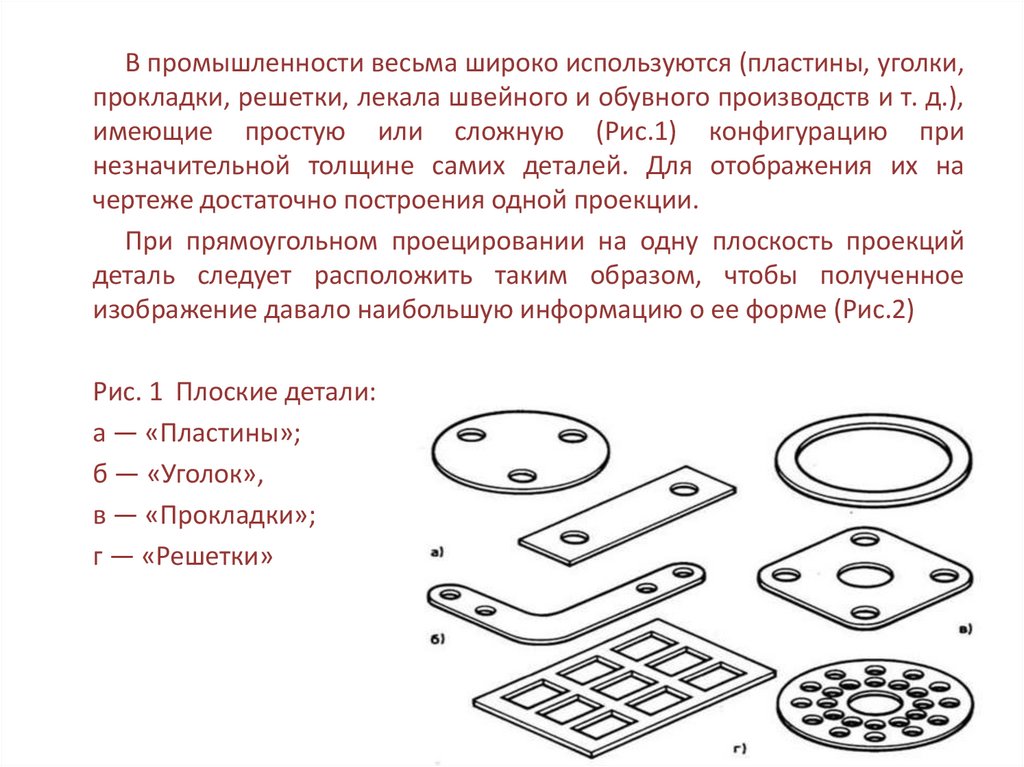
В промышленности весьма широко используются (пластины, уголки,
прокладки, решетки, лекала швейного и обувного производств и т. д.),
имеющие простую или сложную (Рис.1) конфигурацию при
незначительной толщине самих деталей. Для отображения их на
чертеже достаточно построения одной проекции.
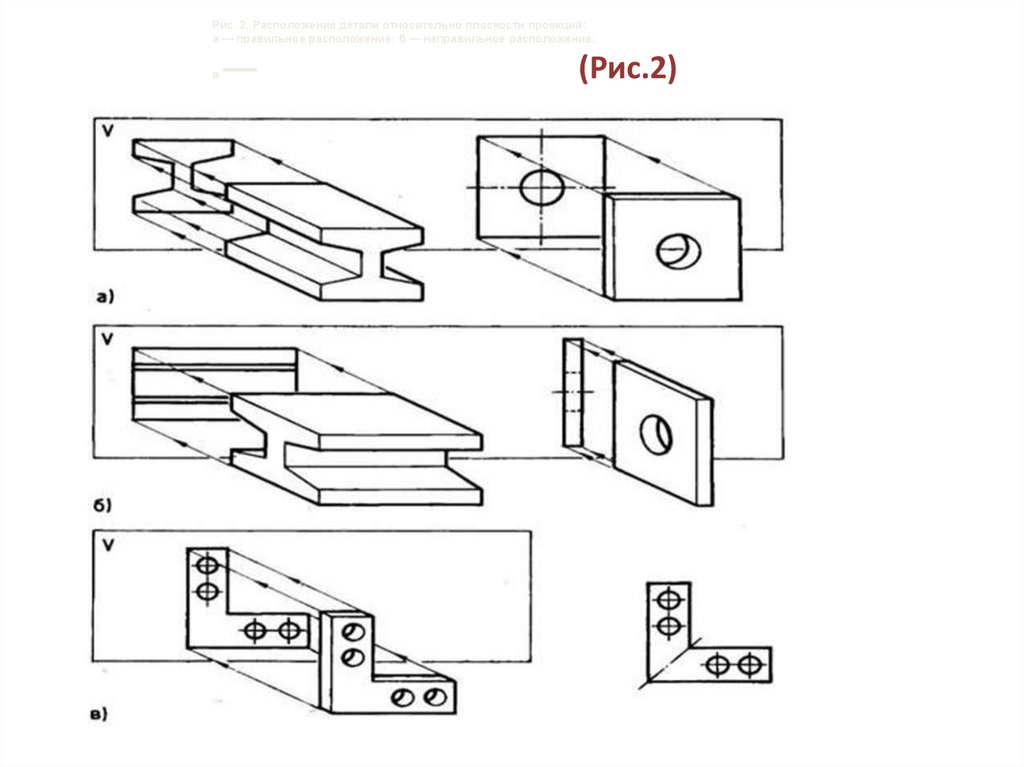
При прямоугольном проецировании на одну плоскость проекций
деталь следует расположить таким образом, чтобы полученное
изображение давало наибольшую информацию о ее форме (Рис.2)
Рис. 1 Плоские детали:
а — «Пластины»;
б — «Уголок»,
в — «Прокладки»;
г — «Решетки»

15.

Рис. 2. Расположение детали относительно плоскости проекций:
а — правильное расположение; б — неправильное расположение;
в
—
(Рис.2)

16.

Для определения точки в пространстве
необходимо иметь две ее параллельные проекции,
полученные при двух различных направлениях
проецирования.

17.

Проецирование на одну плоскость проекций дает
изображение, которое не позволяет однозначно
определить форму и размеры изображенного
предмета.
Наличие
одной
проекции
создает
неопределенность изображения. В таких случаях
говорят о необратимости чертежа, так как по такому
чертежу невозможно воспроизвести оригинал.

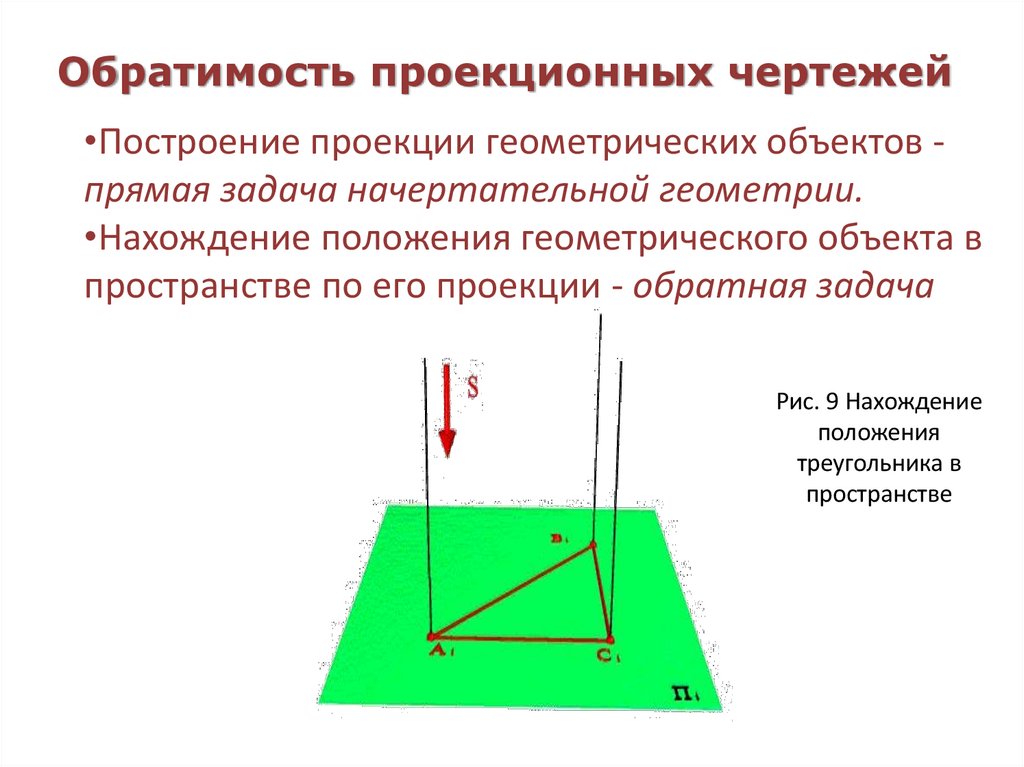
18. Обратимость проекционных чертежей

•Построение проекции геометрических объектов прямая задача начертательной геометрии.
•Нахождение положения геометрического объекта в
пространстве по его проекции - обратная задача
Рис. 9 Нахождение
положения
треугольника в
пространстве

19.

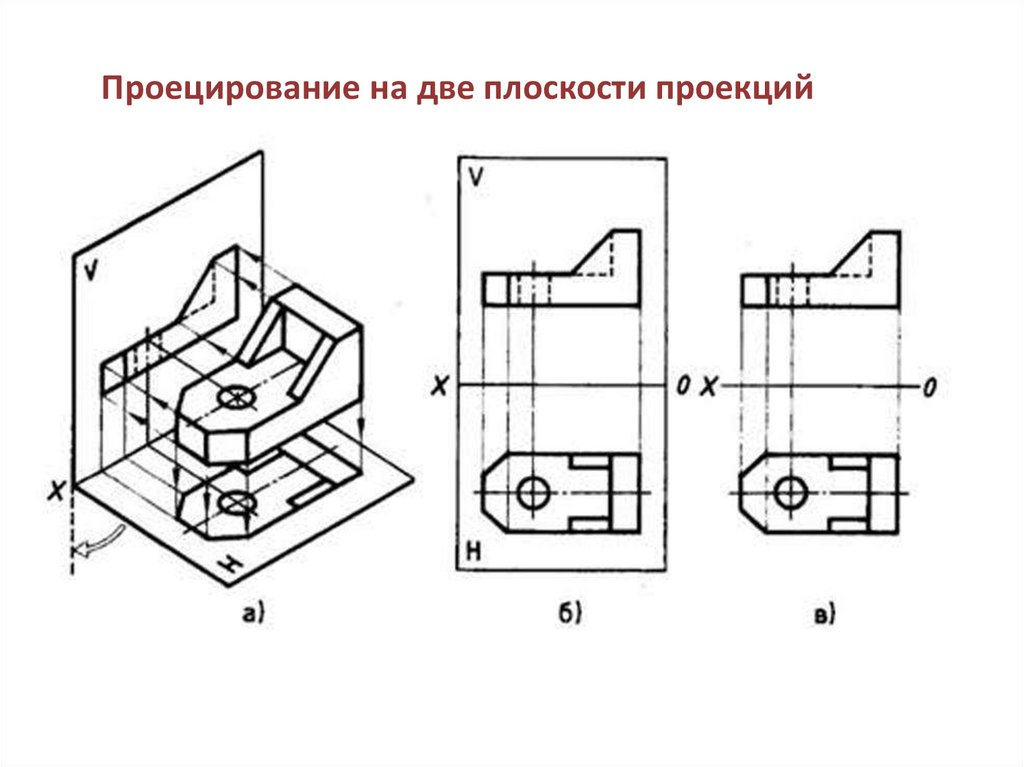
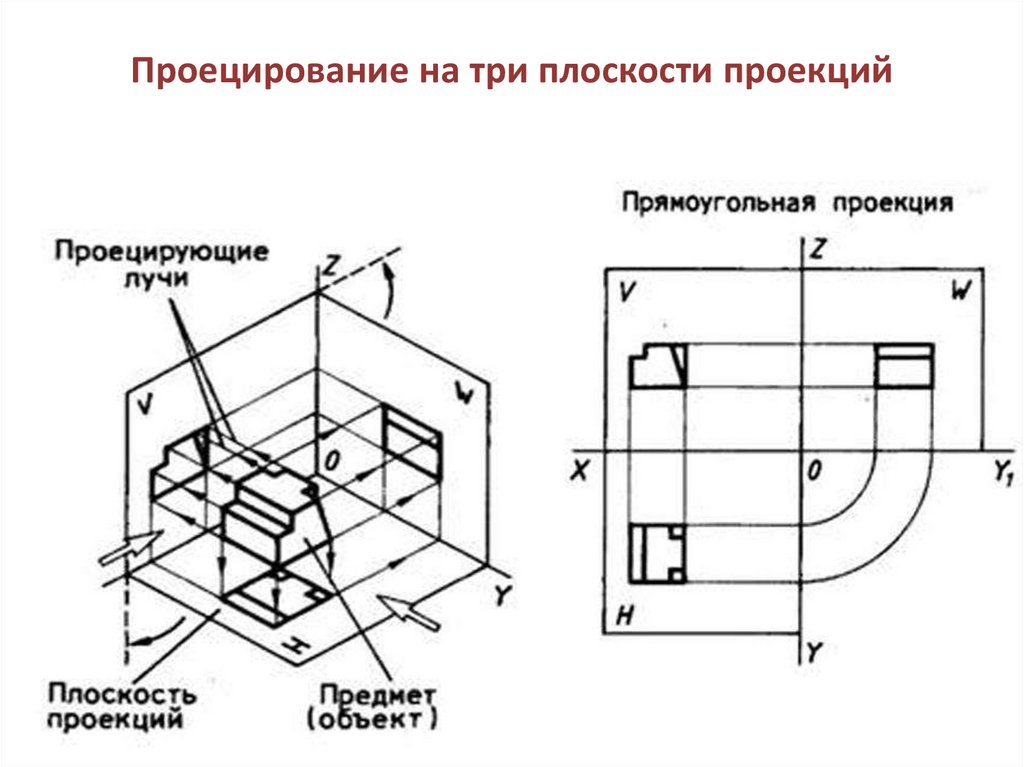
Проецирование на две плоскости проекций

20. Проецирование на три плоскости проекций

21.

• Основные принципы построения таких
чертежей изложены - Гаспаром Монжем,
французским геометром конца 18, начала 19
веков, одним из основателей знаменитой
политехнической школы в Париже и участником
работ по введению метрической системы мер и
весов.
• Изложенный Монжем метод ортогонального
проецирования на две взаимно
перпендикулярные плоскости проекций был и
остается основным методом составления
технических чертежей.

22.

Для определения
точки в пространстве
необходимо иметь
две ее параллельные
проекции, полученные
при двух различных
направлениях
проецирования.

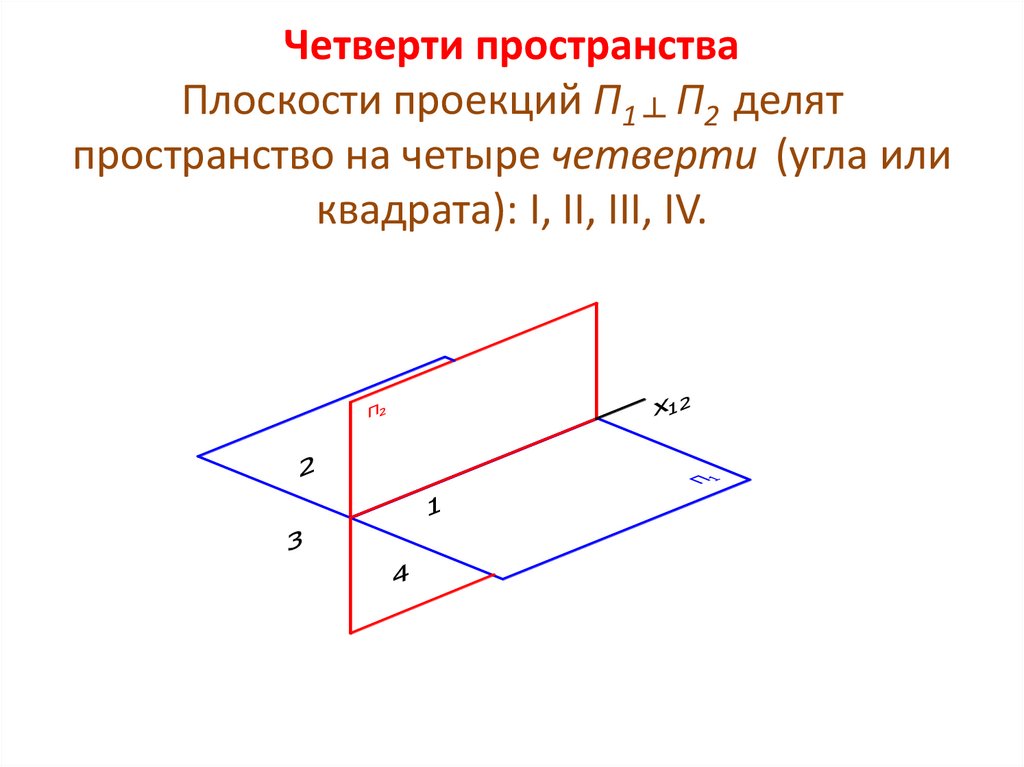
23. Четверти пространства Плоскости проекций П1 ┴ П2 делят пространство на четыре четверти (угла или квадрата): I, II, III, IV.

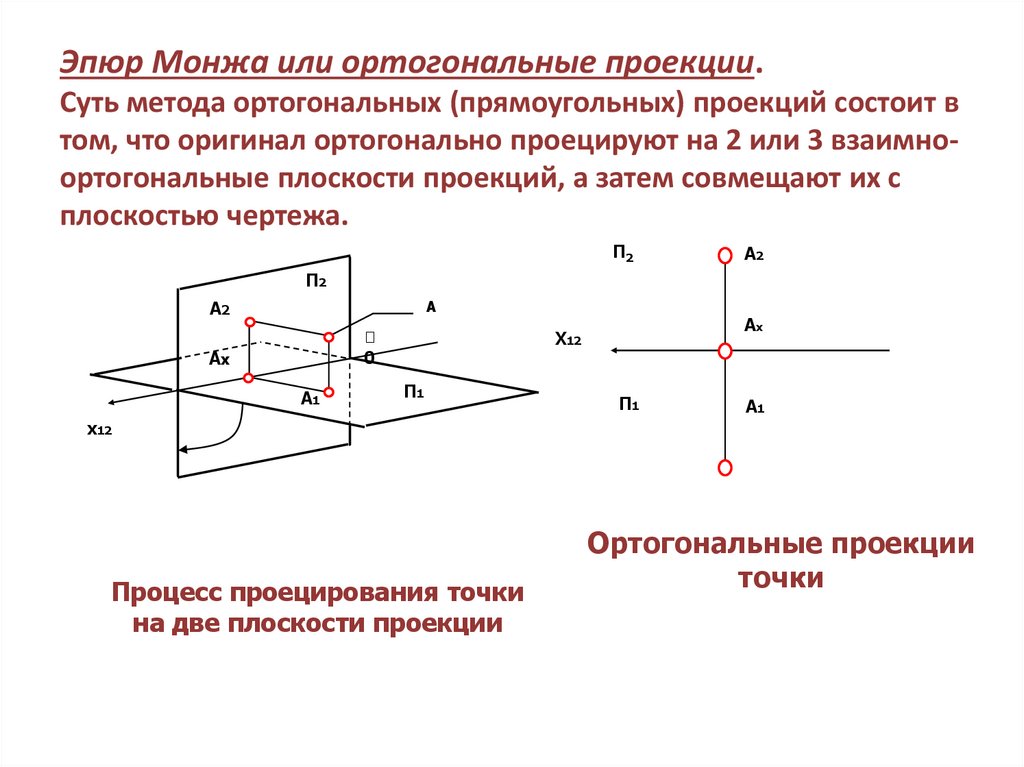
24. Эпюр Монжа или ортогональные проекции. Суть метода ортогональных (прямоугольных) проекций состоит в том, что оригинал

ортогонально проецируют на 2 или 3 взаимноортогональные плоскости проекций, а затем совмещают их с
плоскостью чертежа.
П2
А2
П2
A2
A
0
Ax
A1
Аx
X12
П1
П1
A1
x12
Процесс проецирования точки
на две плоскости проекции
Ортогональные проекции
точки

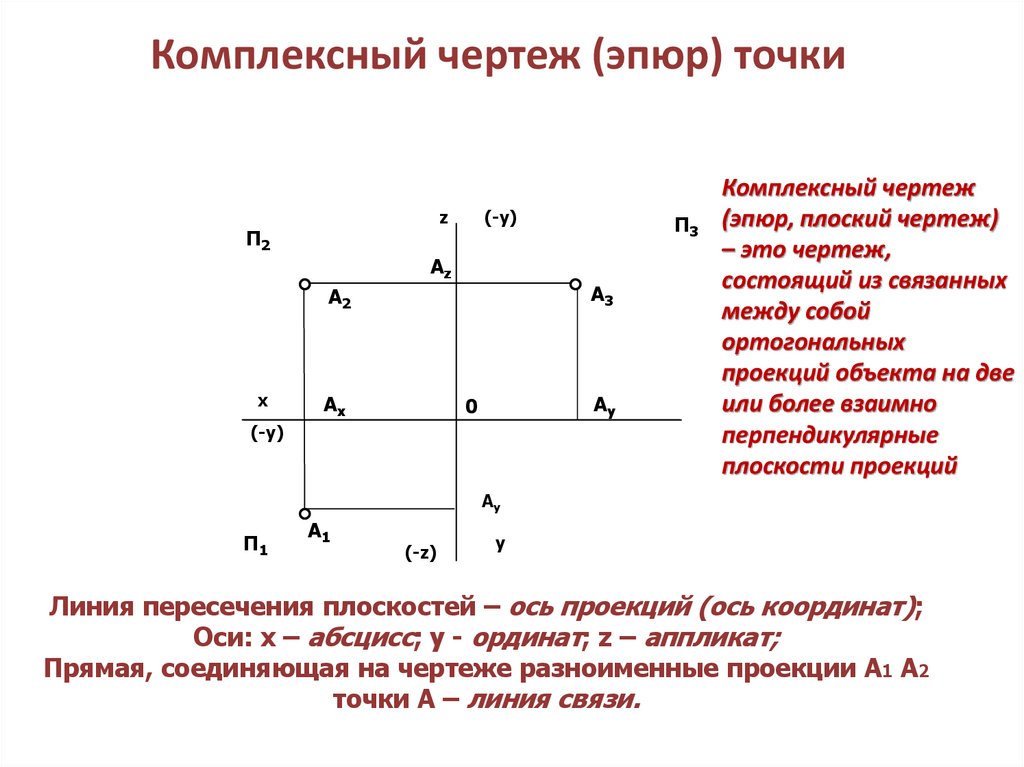
25. Комплексный чертеж (эпюр) точки

z
П2
(-y)
Аz
А3
А2
x
Аx
П3
Аy
0
(-y)
Комплексный чертеж
(эпюр, плоский чертеж)
– это чертеж,
состоящий из связанных
между собой
ортогональных
проекций объекта на две
или более взаимно
перпендикулярные
плоскости проекций
Аy
П1
А1
(-z)
y
Линия пересечения плоскостей – ось проекций (ось координат);
Оси: х – абсцисс; у - ординат; z – аппликат;
Прямая, соединяющая на чертеже разноименные проекции А1 А2
точки А – линия связи.

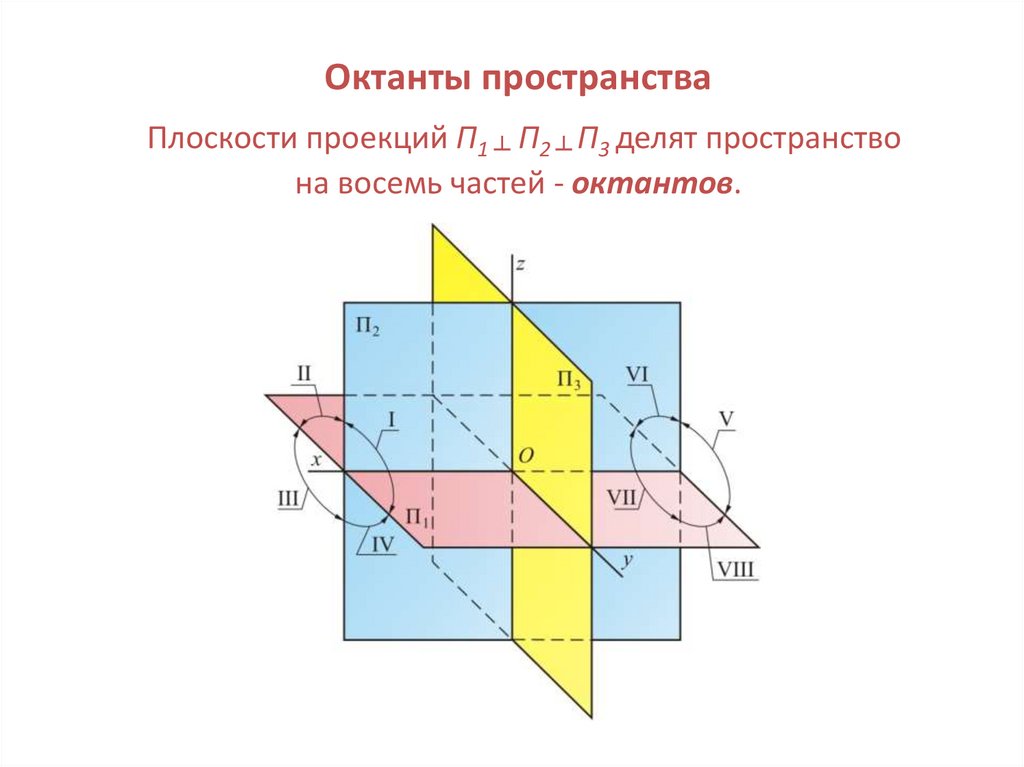
26. Октанты пространства Плоскости проекций П1 ┴ П2 ┴ П3 делят пространство на восемь частей - октантов.

27.

z
П2
-y
П3
z
П2
А2
Аz
А2
А3
x
А
Аy
Аx
x
А3
Аz
А1
П1
0
Аx
y
-y
y
П3
Аy
П1
А1
Аy
-z
y
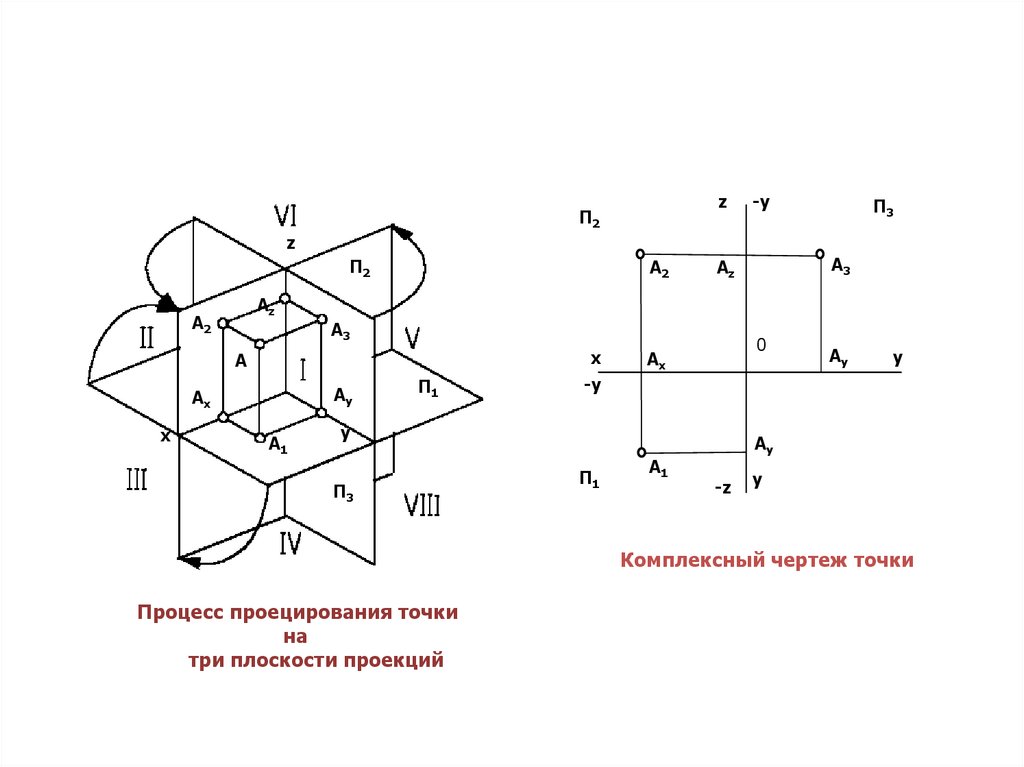
Комплексный чертеж точки
Процесс проецирования точки
на
три плоскости проекций

28.

Теоремы
Положение точки в пространстве вполне
определяется ее ортогональными проекциями на
две плоскости.
Если точка принадлежит плоскости проекций, то
одна из ее проекций совпадает с точкой, а две
другие находятся на осях координат.
Если точка пространства принадлежит
биссекторной плоскости, то ее горизонтальная и
фронтальная проекции равноудалены от оси.

29. Теоремы

ТОЧКА
Задача 1. 1
Построить комплексный чертеж точек А (координаты точки А в таблице 1).
Задача 1. 2
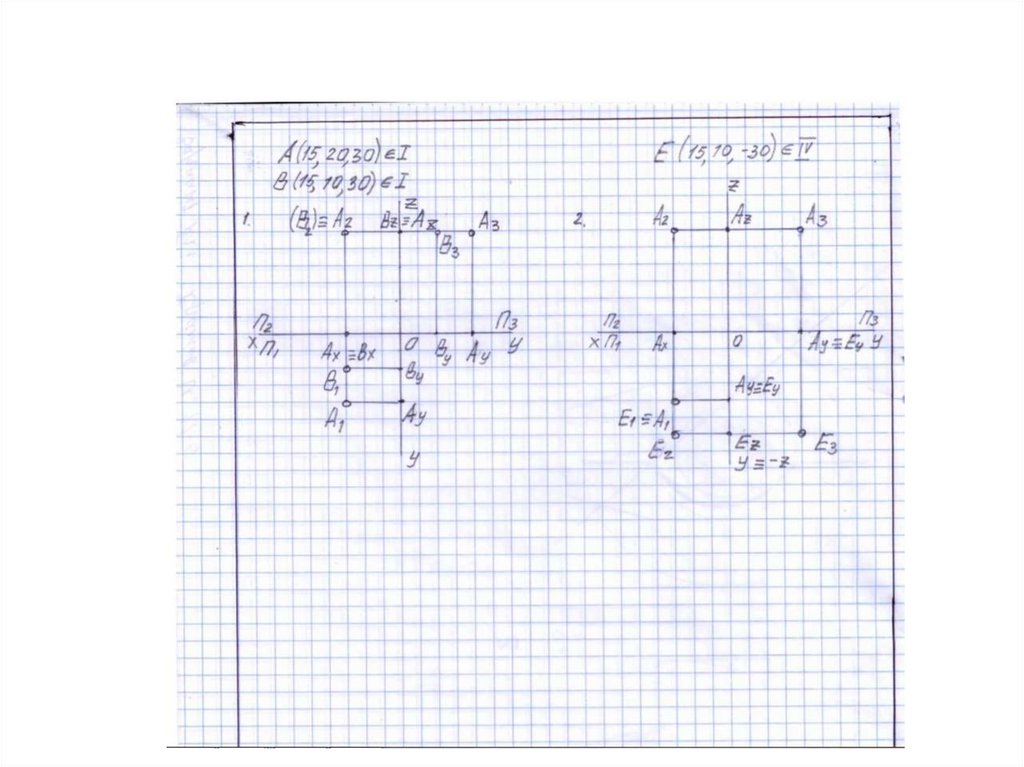
Построить комплексный чертеж точек А и В (координаты точки А в таблице 1).
Точка В расположена дальше от плоскости П1 (для четных) и ближе к
плоскости П2 (для нечетных вариантов) на 10 мм, чем точка А.
Задача 1.3.
Построить комплексный чертеж точек А (координаты точки А в таблице 1) и С,
которая симметрична точке А относительно горизонтальной плоскости
проекций.
Задача 1.4.
Построить комплексный чертеж точек А (координаты точки А в таблице 1) и D,
которая симметрична точке А относительно фронтальной плоскости
проекций.
Задача 1.5.
Построить комплексный чертеж точек А (координаты точки А в таблице 1) и E,
которая симметрична точке А относительно оси х.

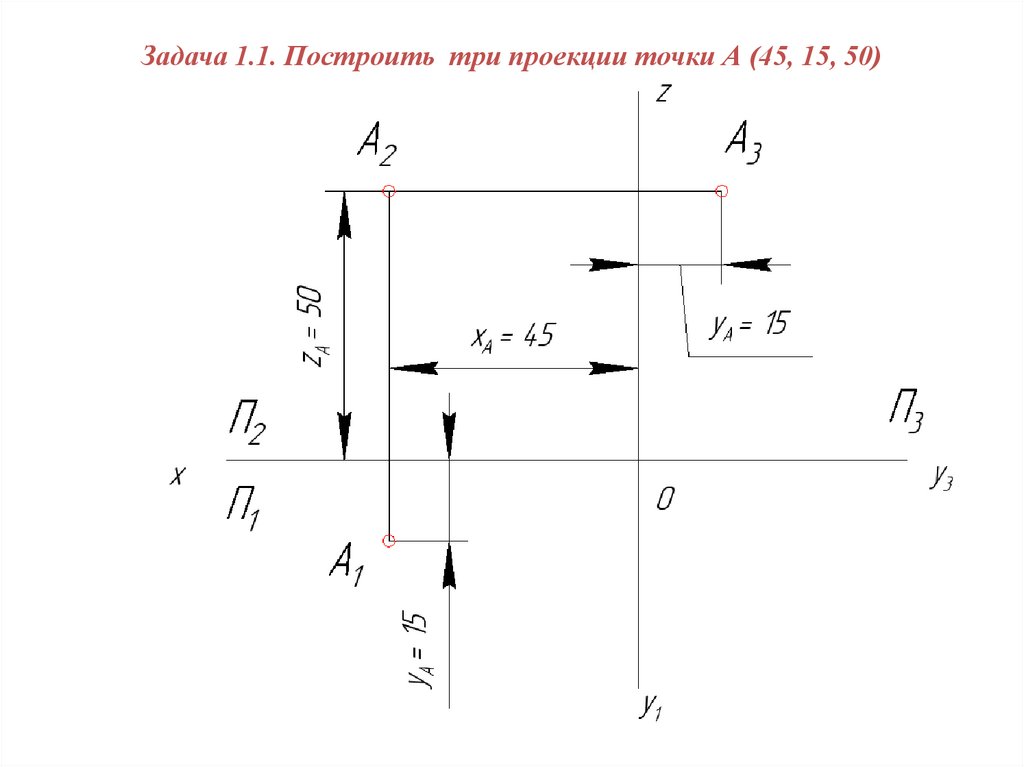
30. ТОЧКА

Задача 1.1. Построить три проекции точки А (45, 15, 50)

31.

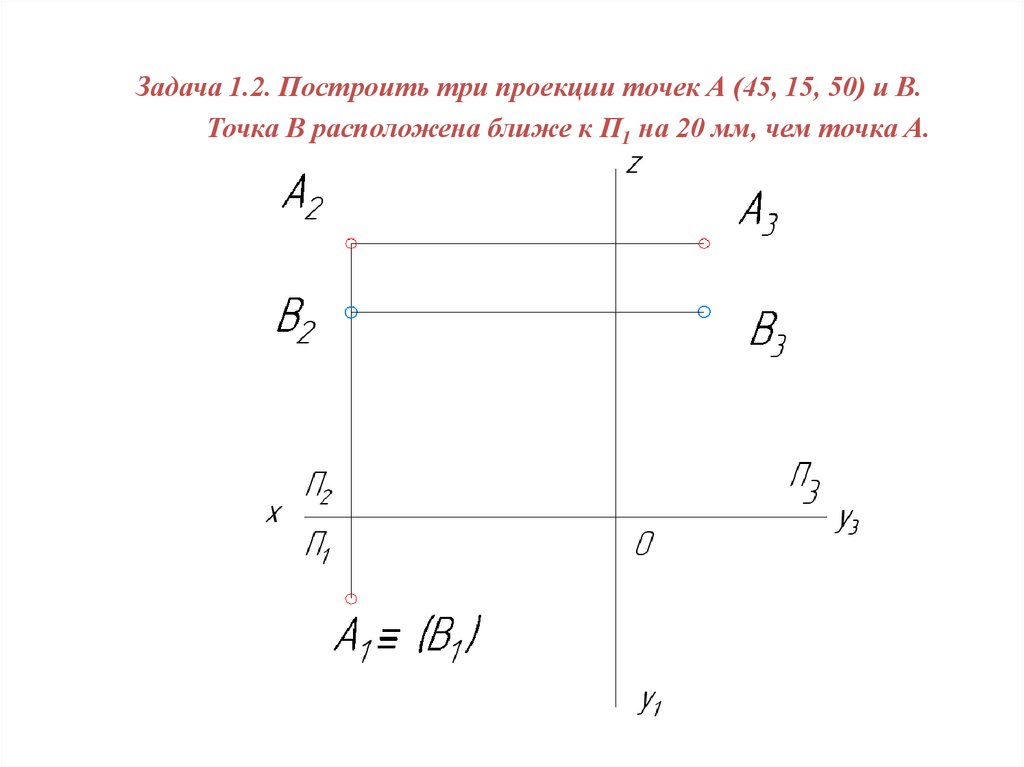
Задача 1.2. Построить три проекции точек А (45, 15, 50) и В.
Точка В расположена ближе к П1 на 20 мм, чем точка А.

32.

Задача 1.3. Построить три проекции точек А и С. Точка С расположена
симметрично точке А относительно горизонтальной плоскости
проекций

33.

Задача 1.4. Построить три проекции точек А и D. Точка D расположена
симметрично точке А относительно фронтальной плоскости проекций П2

34. Задача 1.4. Построить три проекции точек А и D. Точка D расположена симметрично точке А относительно фронтальной плоскости

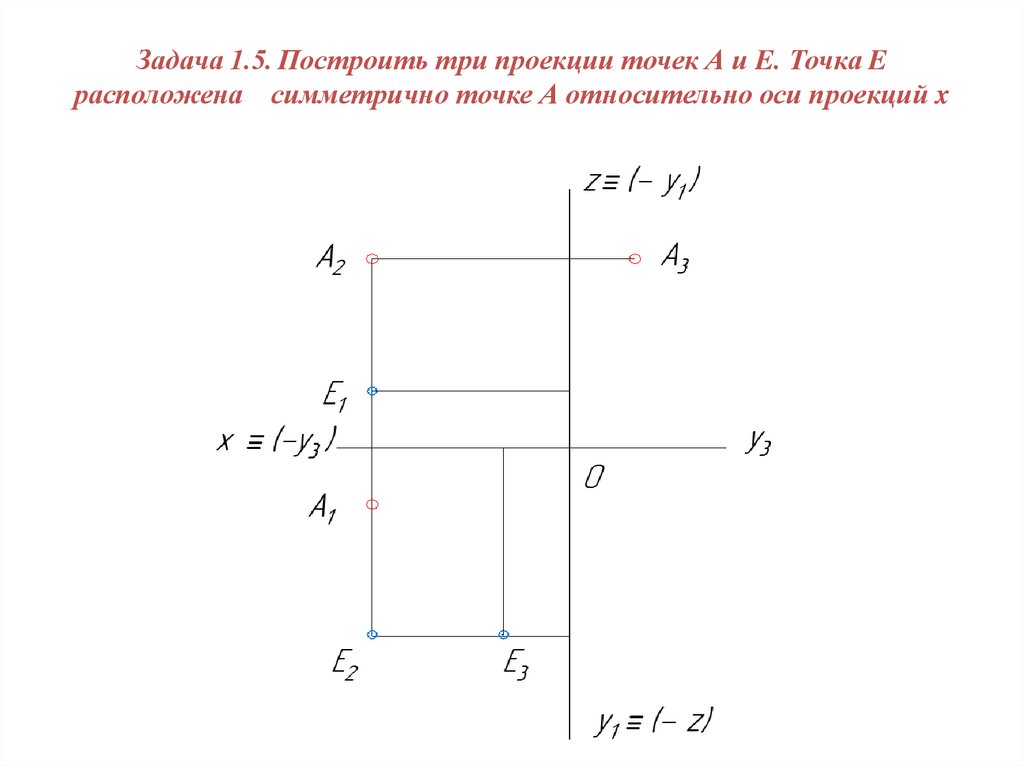
Задача 1.5. Построить три проекции точек А и E. Точка E
расположена симметрично точке А относительно оси проекций x