Похожие презентации:
Функции. анализ. Элементарные функции
1.
Математический8. Функции.
анализ
Элементарные
функции.
2.
Область определения D(f) функции- множество на котором функция задана и
определена.
1
g ( x) 0
y
g ( x)
y log a g ( x) g ( x) 0
y arcsin g ( x)
y 2 n g ( x) g ( x ) 0
y arccos g ( x) g ( x) 1
y tg ( g ( x)) g ( x)
2
n, n Z
y сtg ( g ( x)) g ( x) n, n Z
3.
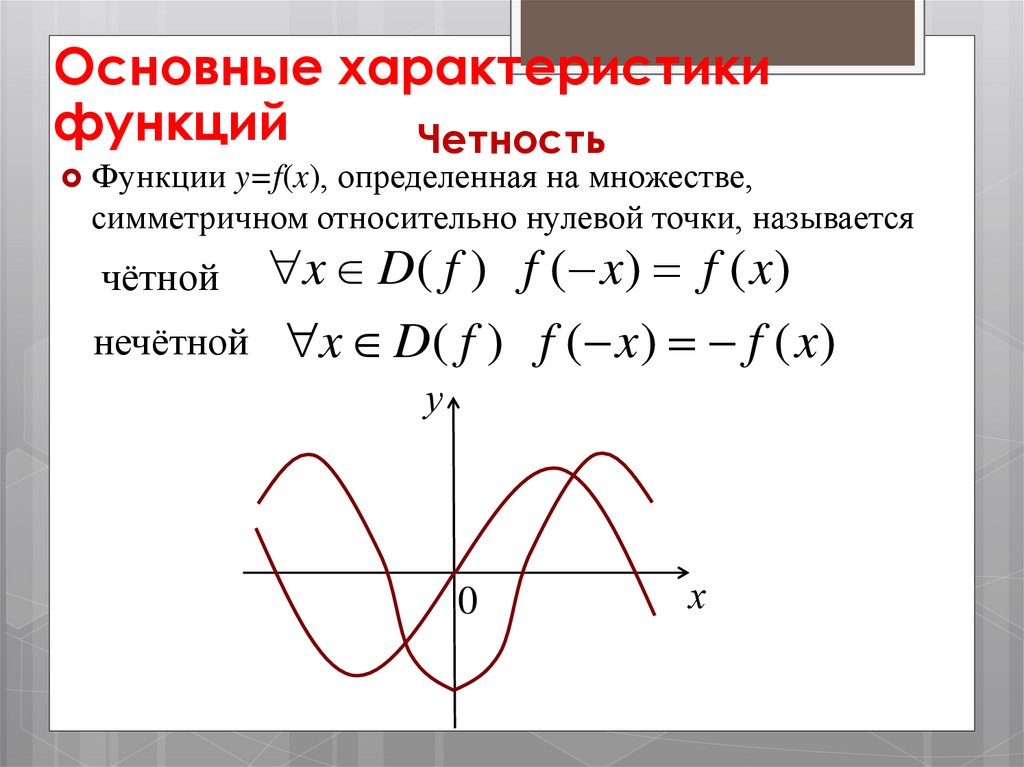
Основные характеристикифункций
Четность
Функции y=f(x), определенная на множестве,
симметричном относительно нулевой точки, называется
x D( f ) f ( x) f ( x)
нечётной x D( f ) f ( x) f ( x)
чётной
у
0
х
4.
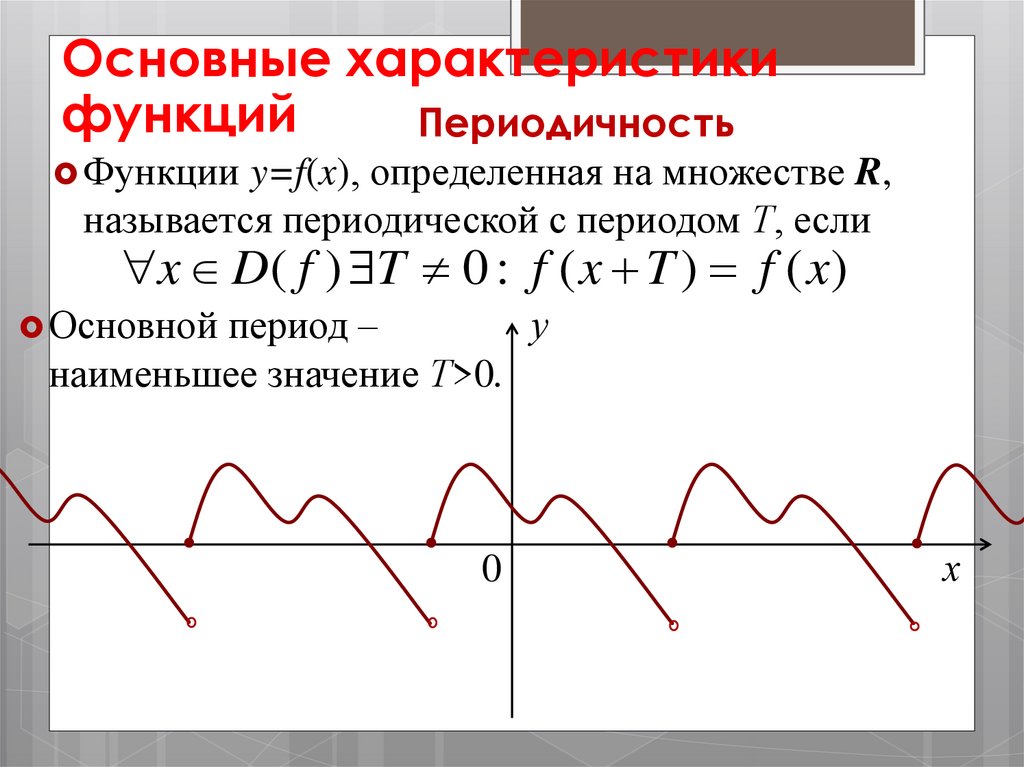
Основные характеристикифункций
Периодичность
Функции y=f(x), определенная на множестве R,
называется периодической с периодом Т, если
x D( f ) T 0 : f ( x T ) f ( x)
Основной период –
у
наименьшее значение Т>0.
0
х
5.
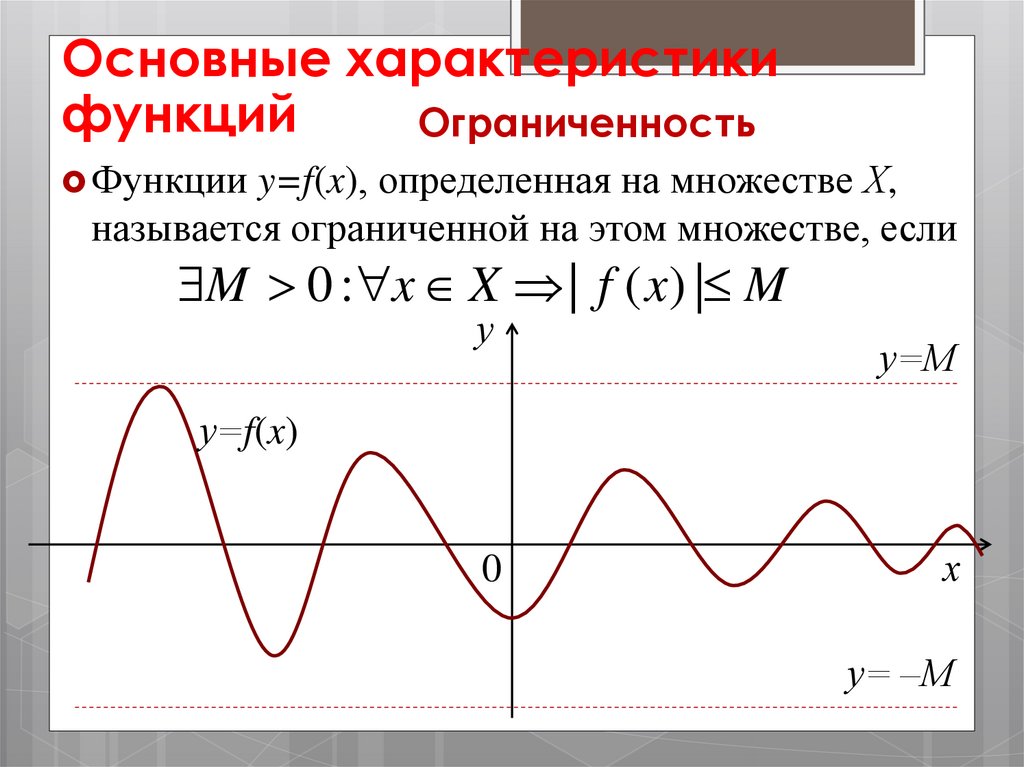
Основные характеристикифункций
Ограниченность
Функции y=f(x), определенная на множестве Х,
называется ограниченной на этом множестве, если
M 0 : x X | f ( x) | M
у
у=М
у=f(x)
0
х
у= –М
6.
Основные характеристикифункций
Монотонность
Функции y=f(x), определенная на множестве Х,
является
x1 , x2 X : x1 x2
возрастающей
убывающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
строго монотонные функции
неубывающией
невозрастающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
монотонные функции
7.
Сложная функция (функция отфункции или суперпозиция функций)
g: X D
f : D Y f (g) : X Y
y f (u ), u g ( x) y f ( g ( x))
промежуточный
аргумент
сложная функция
y f1 ( f 2 ( f 3 (...( f n ( x))...)))
y sin x
2
y sin u
y sin x (sin x)
2
2
y u
u x
2
2
u sin x
8.
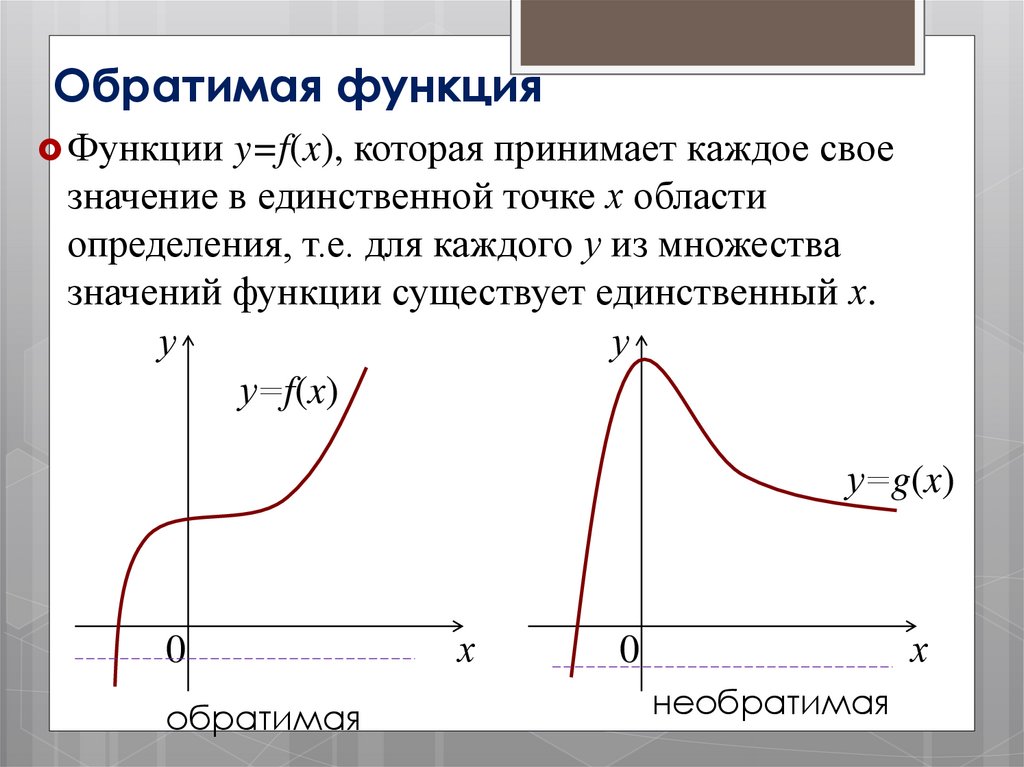
Обратимая функцияФункции y=f(x), которая принимает каждое свое
значение в единственной точке х области
определения, т.е. для каждого у из множества
значений функции существует единственный х.
у
у
у=f(x)
у=g(x)
0
обратимая
х
х
0
необратимая
9.
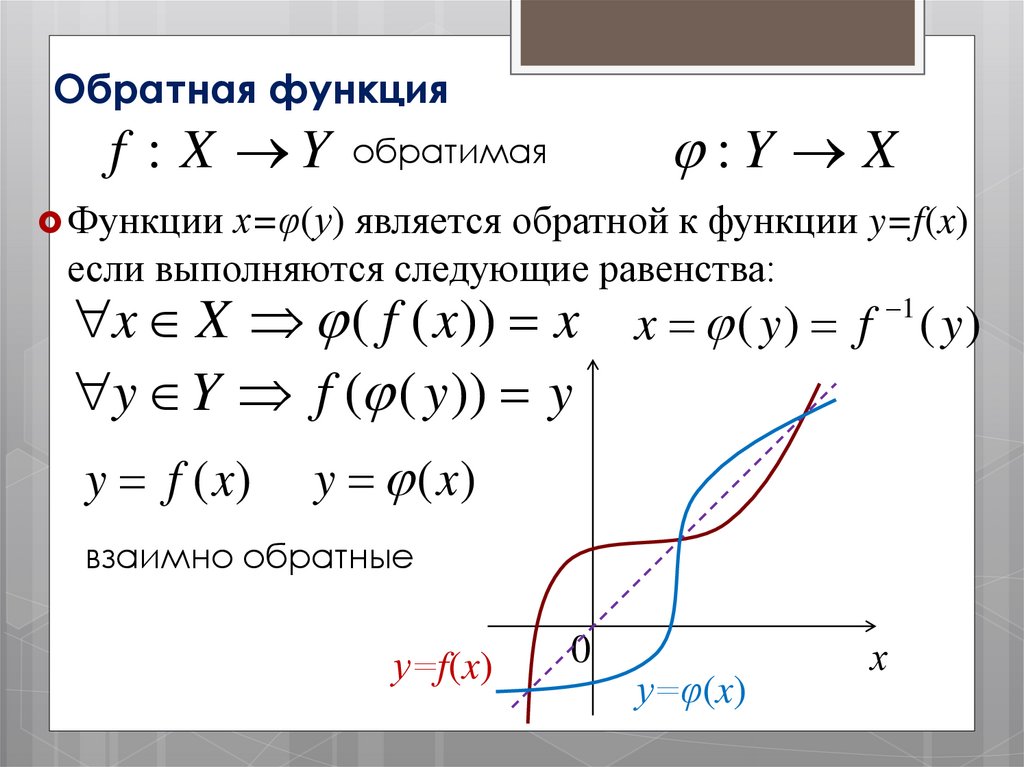
Обратная функция:Y X
f : X Y обратимая
Функции х=φ(у) является обратной к функции y=f(x)
если выполняются следующие равенства:
x X ( f ( x)) x
y Y f ( ( y )) y
y f (x)
x ( y) f ( y)
1
y (x)
взаимно обратные
у=f(x)
0
у=φ(x)
х
10.
Основные (простейшие)элементарные функции
Степенная функция y x , R
n N Dom( f ) R параболы порядка п
n Dom( f ) R \ {0} гиперболы порядка п
1
корень
Dom( f ) : x 0 арифметический
степени п
n
m
Dom( f ) : x 0
n
y x
n
m
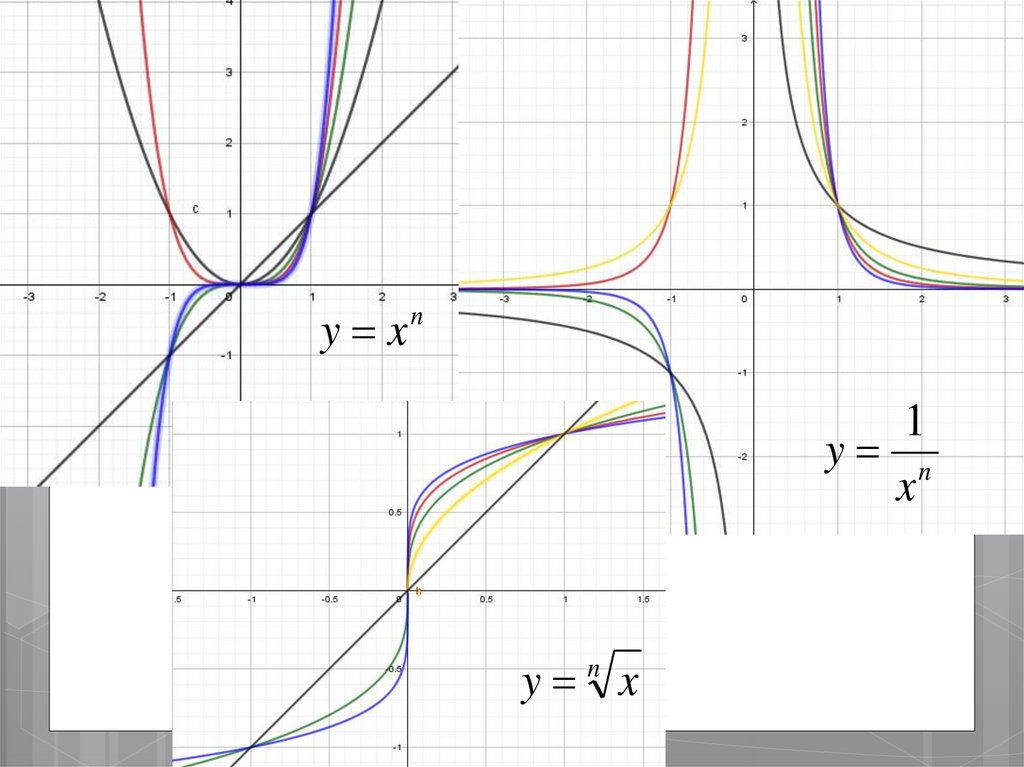
11.
y xn1
y n
x
y n x
12.
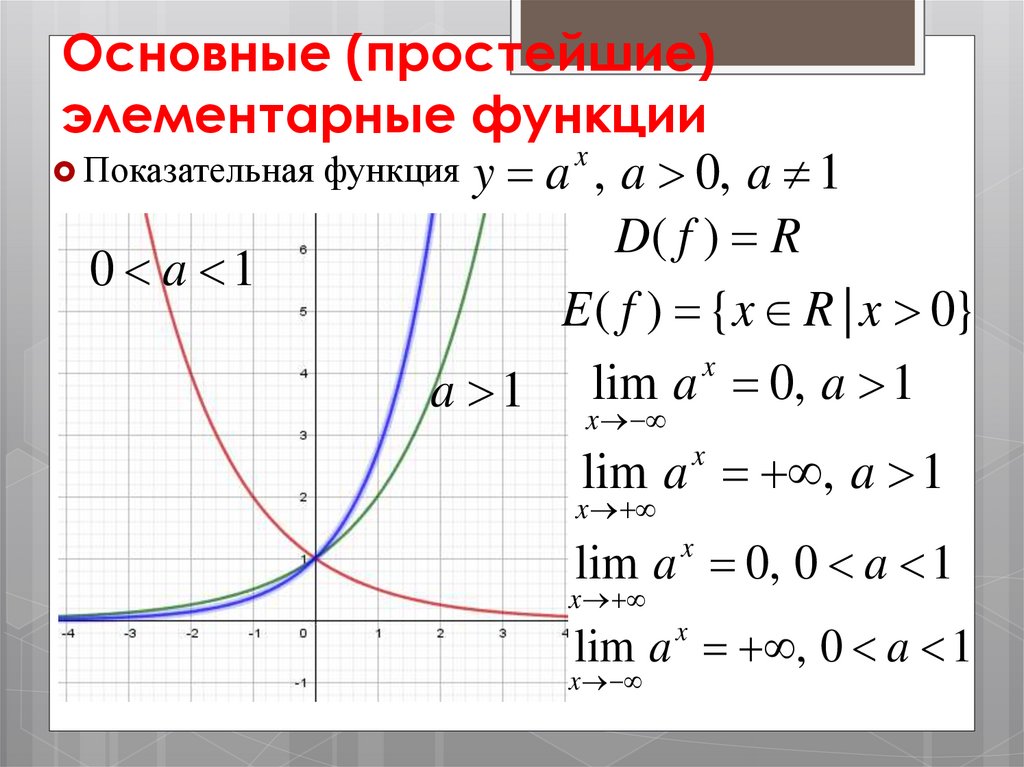
Основные (простейшие)элементарные функции
x
Показательная функция y a , a 0, a 1
D( f ) R
0 a 1
E ( f ) {x R | x 0}
x
a 1 lim a 0, a 1
x
lim a , a 1
x
x
lim a 0, 0 a 1
x
x
lim a , 0 a 1
x
x
13.
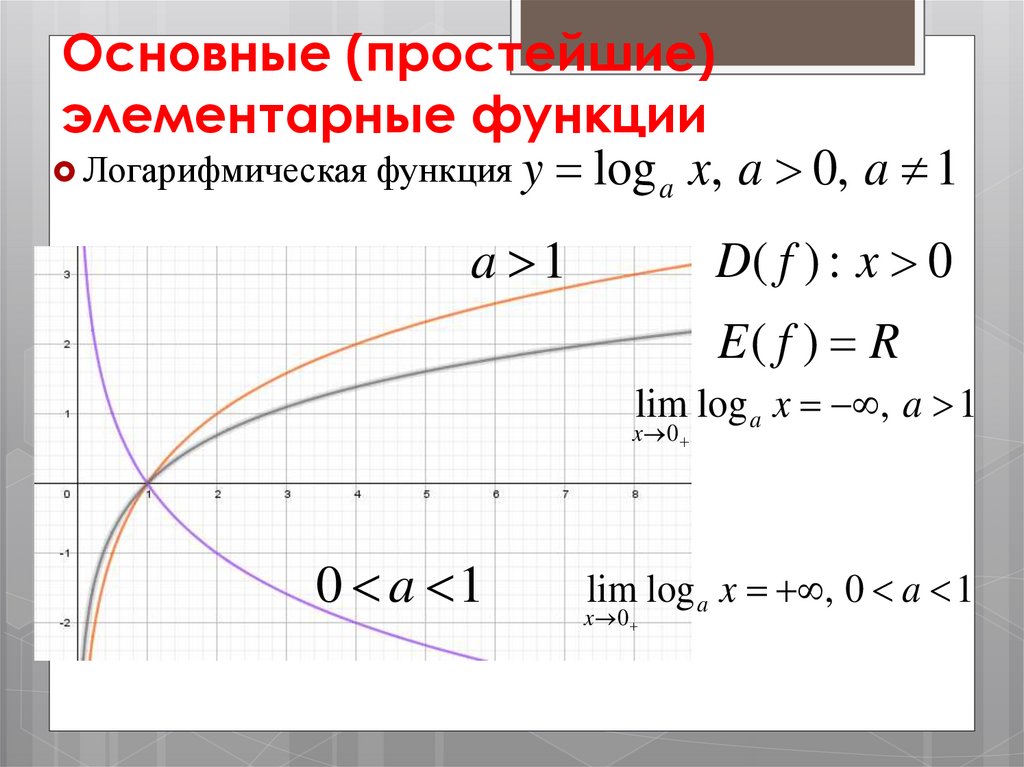
Основные (простейшие)элементарные функции
Логарифмическая функция y log x, a 0, a 1
a
a 1
D( f ) : x 0
E( f ) R
lim log a x , a 1
x 0
0 a 1
lim log a x , 0 a 1
x 0
14.
Основные (простейшие)элементарные функции
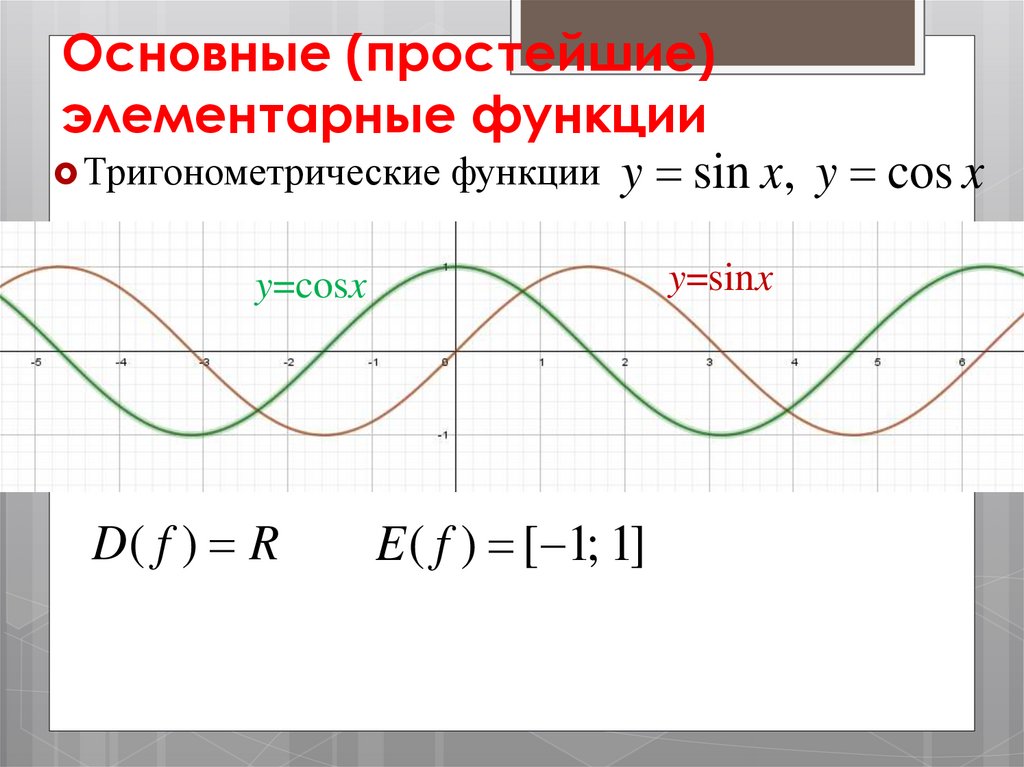
Тригонометрические функции y sin x, y cos x
y=sinx
y=cosx
D( f ) R
E ( f ) [ 1; 1]
15.
Основные (простейшие)элементарные функции
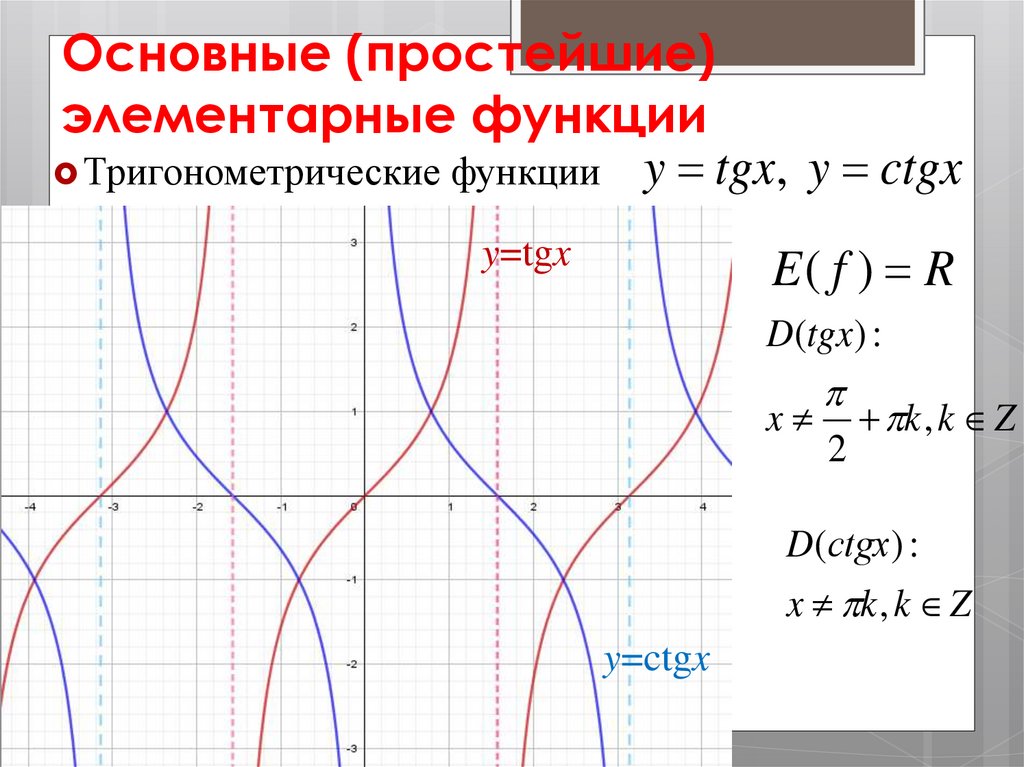
Тригонометрические функции y tgx, y ctgx
E( f ) R
y=tgx
D(tgx) :
x k , k Z
2
D(сtgx) :
x k , k Z
y=ctgx
16.
Основные (простейшие)элементарные функции
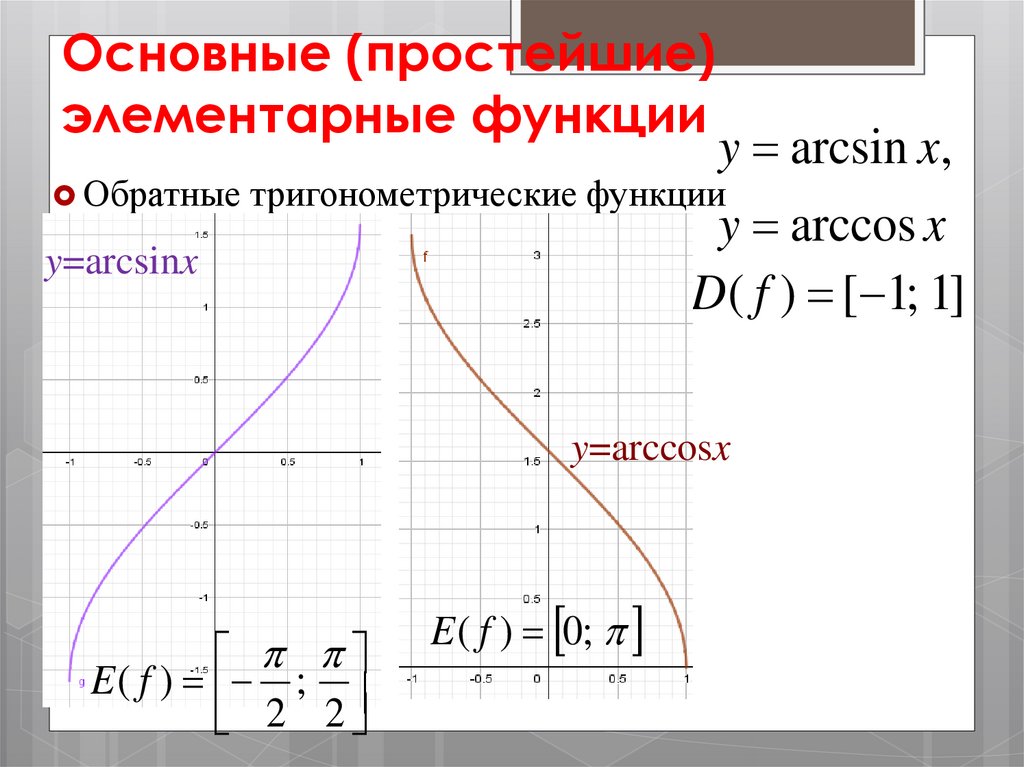
y arcsin x,
Обратные тригонометрические функции
y arccos x
y=arcsinx
D( f ) [ 1; 1]
y=arccosx
E ( f ) ;
2 2
E ( f ) 0;
17.
Основные (простейшие)элементарные функции
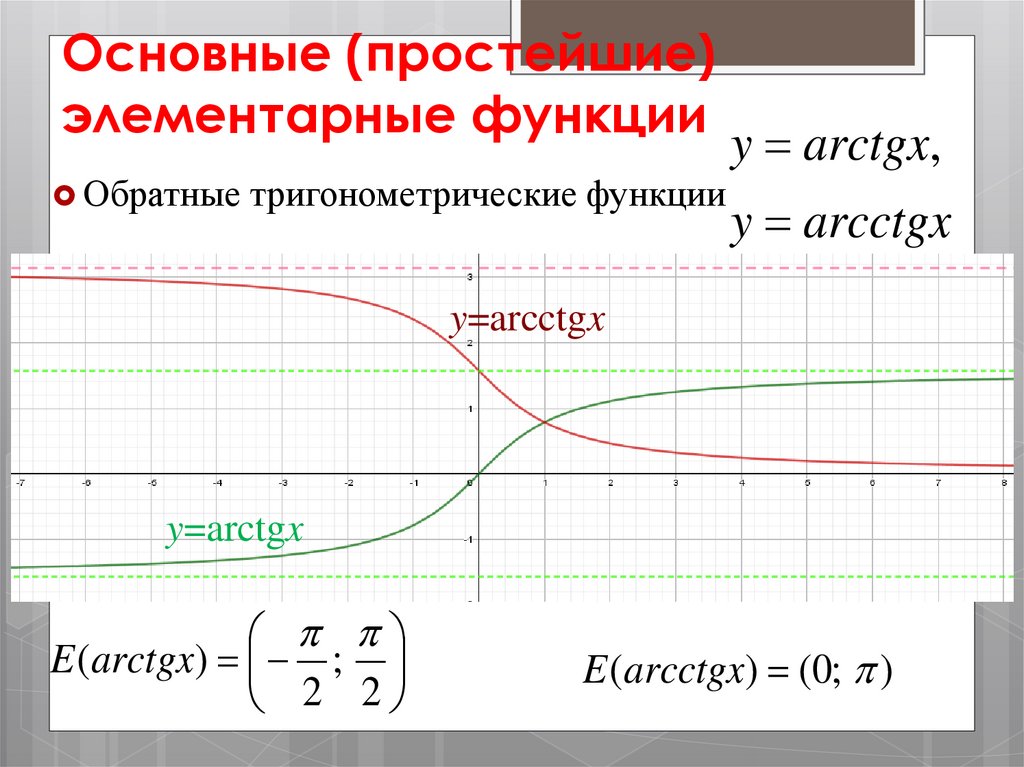
y arctgx,
Обратные тригонометрические функции
y arcctgx
D
(
f
)
R
y=arcctgx
y=arctgx
E (arctgx) ;
2 2
E (arcctgx) (0; )
18.
Элементарные функцииФункции, задаваемые одной формулой,
составленной из основных элементарных
функций и постоянных с помощью конечного
числа арифметических операций и операций
взятия функции от функции.
y log 2
x 2
x 2 1 y x arcsin 3 sin 2 (ln x ) Элементарные
2
3
x
x 8
функции
x, x 0,
y | x 2 | y x y
2
1
x
,x 0
2 n 1
x3 x5
x
y x ... ( 1) n
...
2! 4!
(2n)!
Неэлементарные
функции
19.
Математическийанализ
9. Локальная и
глобальная
непрерывность
функций в точке
20.
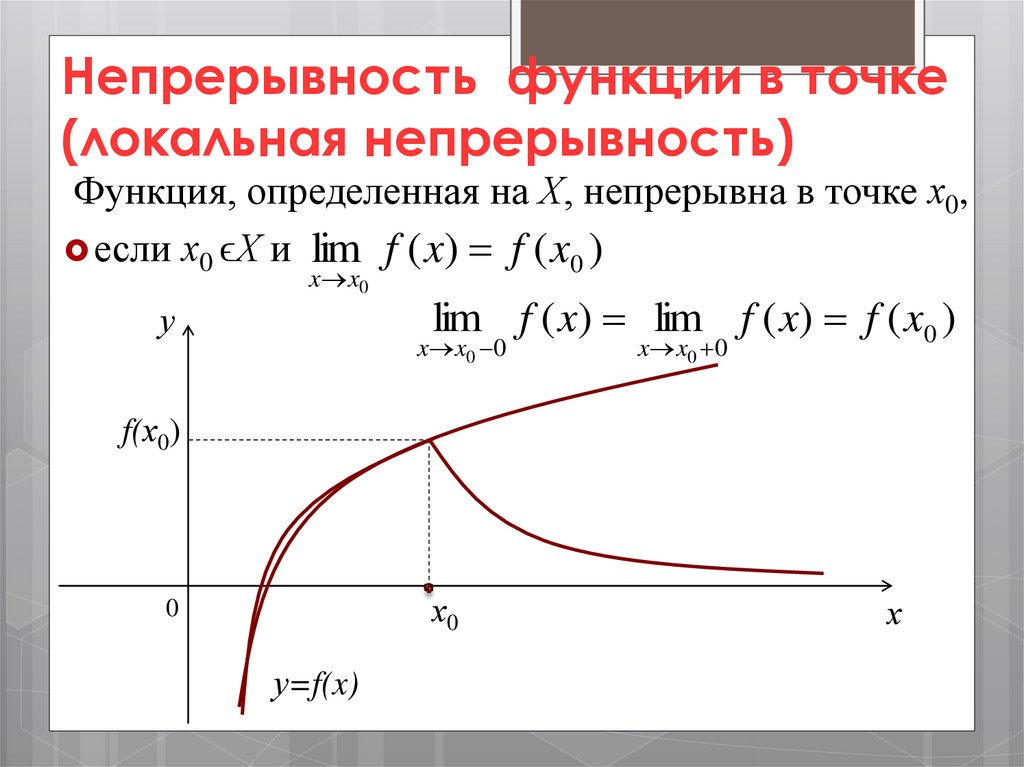
Непрерывность функции в точке(локальная непрерывность)
Функция, определенная на Х, непрерывна в точке х0,
если х0 ϵХ и lim f ( x) f ( x0 )
x x0
у
lim f ( x) lim f ( x) f ( x0 )
x x0 0
x x0 0
f(х0)
х0
0
у=f(x)
х
21.
lim f ( x) f ( x0 )x x0
lim x x0
x x0
lim f ( x) f ( lim x) f ( x0 )
x x0
x x0
При нахождении предела непрерывной функции
y=f(x) можно перейти к пределу под знаком
функции, т.е. вместо аргумента х в функцию
y=f(x) подставить его предельное значение: х0.
22.
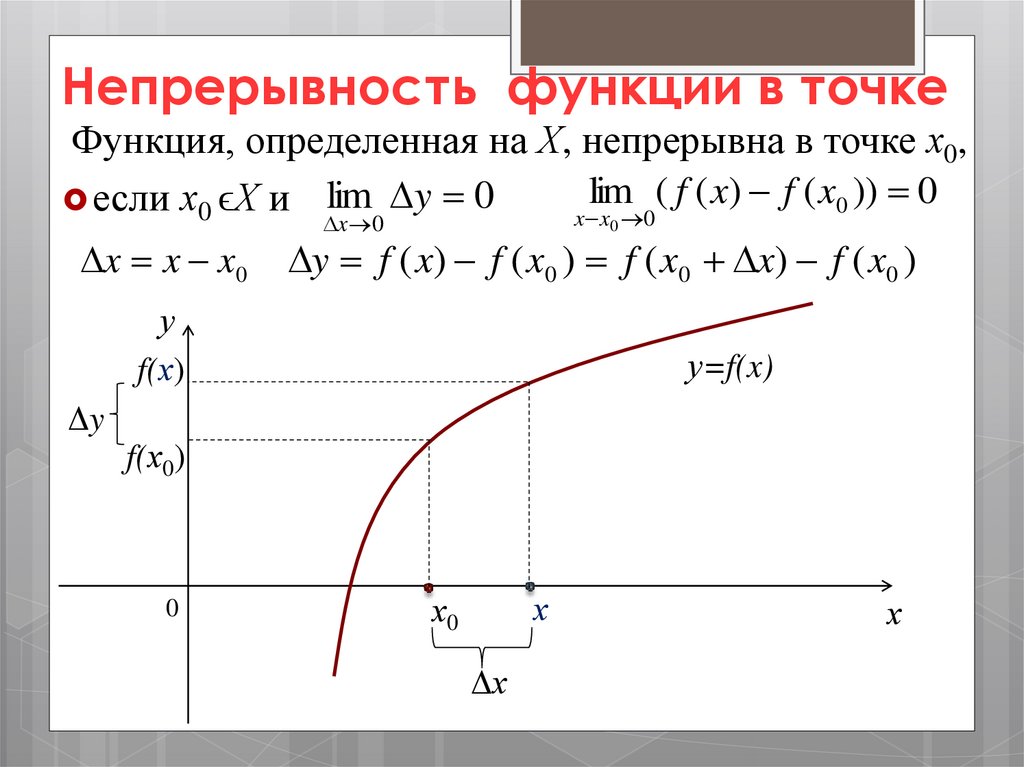
Непрерывность функции в точкеФункция, определенная на Х, непрерывна в точке х0,
если х0 ϵХ и lim f ( x) f ( x0 )
x x0
если х0 ϵХ и если
xn x0 f ( xn ) f ( x0 )
если
0 0 x X :
f ( х) f ( х0 )
x x0
lim ( f ( x) f ( x0 )) 0
x x0 0
x x x0
y f ( x) f ( x0 )
23.
Непрерывность функции в точкеФункция, определенная на Х, непрерывна в точке х0,
lim ( f ( x) f ( x0 )) 0
если х0 ϵХ и lim y 0
x x 0
x x x0
x 0
0
y f ( x) f ( x0 ) f ( x0 x) f ( x0 )
у
f(х)
у=f(x)
Δy
f(х0)
0
х
х0
Δх
х
24.
Свойства непрерывных функций1. f(x) и g(x) – непрерывны в точке х0
f ( x)
непрерывны
f ( x) g ( x), f ( x) g ( x), f ( x) g ( x),
( g ( x0 ) 0) в точке х
0
g ( x)
1. Сумма, разность, произведение и частное (знаменатель
не обращается в нуль) конечного числа функций,
непрерывных в некоторой точке, является функцией,
непрерывной в той же точке.
2. Сложная функция, составленная из конечного числа
непрерывных функций, непрерывна.
В частности, если функция f непрерывна в точке х0, а
функция g непрерывна в точке у0=f(х0), то и их композиция
g(f(x)) непрерывна в точке х0.
3. Функция, обратная к строго монотонной и непрерывной
функции, непрерывна.
25.
Точки разрываПусть функция определена в некоторой
окрестности точки х0, кроме, быть может, самой
точки х0.
Тогда х0 называется точкой разрыва функции
если функция в этой точке не является
непрерывной, т.е. функция
1) или не определена в самой точке х0,
2) или функция определена в точке х0, но
lim f ( x) f ( x0 )
x x0
lim y 0
x 0
26.
Точки разрывау
lim y 0
x 0
f(х2)
Δy2
f(х1)
у=f(x)
Δy1
f(х0)
0
х 0 х2
Δх
х1
х
27.
Классификация точек разрываlim f ( x) f ( x0 )
x x0
lim f ( x) a,
x x0 0
lim f ( x) b
x x0 0
Точка разрыва 1 рода
Точка разрыва 2 рода
a R b R
a b
a не сущ. b не сущ.
Точка
устранимого
разрыва
Точка
конечного
разрыва
a b, f ( x0 ) a
a b
Если f(x0)=a,
то разрыв
устранен.
| a b|
скачек функции в точке
разрыва 1 рода.
28.
Непрерывность функции на промежутке(глобальная непрерывность)
Функция называется непрерывной на интервале, если
она непрерывна в каждой точке этого интервала.
Функция называется непрерывной на отрезке [a; b],
если она непрерывна в каждой точке интервала (a; b)
и выполняется односторонняя непрерывность на
концах отрезка, т.е.
lim f ( x) f (a), lim f ( x) f (b)
x a 0
x b 0
Любая элементарная функция непрерывна в тех
интервалах, где она определена.
29.
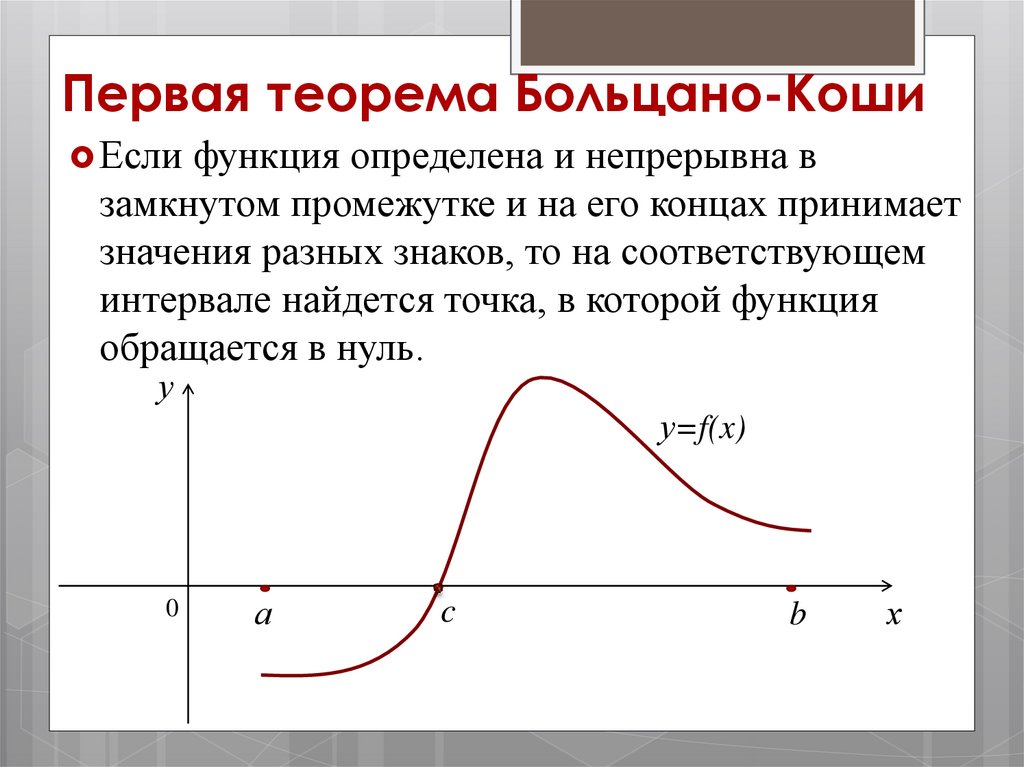
Первая теорема Больцано-КошиЕсли функция определена и непрерывна в
замкнутом промежутке и на его концах принимает
значения разных знаков, то на соответствующем
интервале найдется точка, в которой функция
обращается в нуль.
у
у=f(x)
0
а
c
b
х
30.
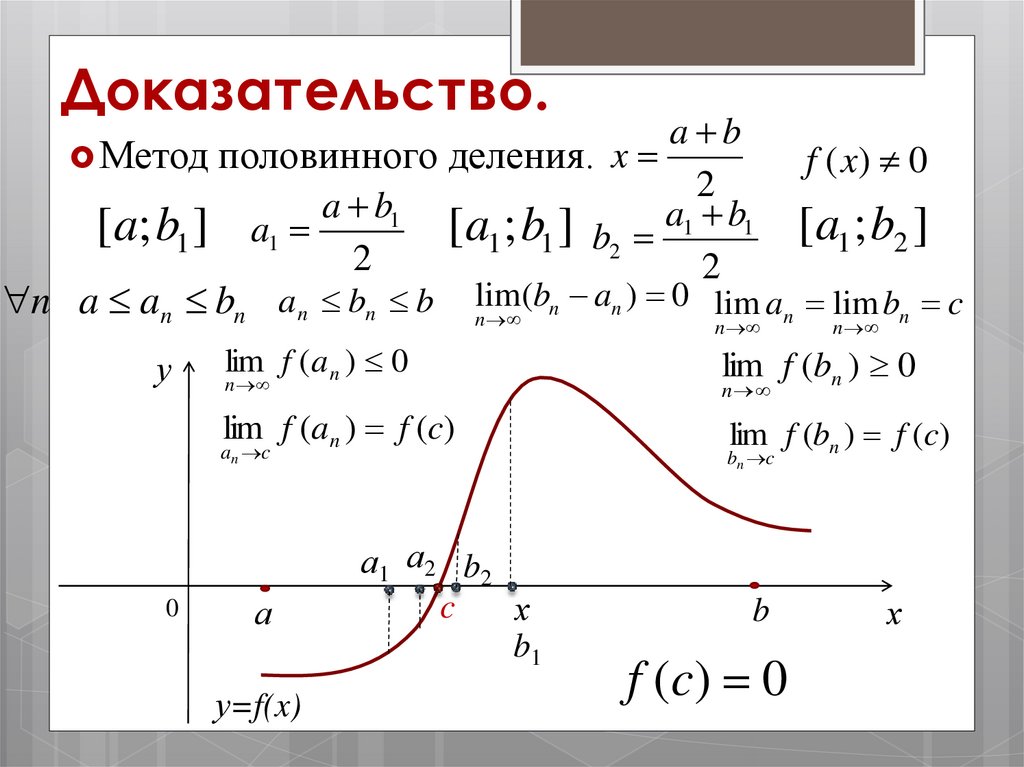
Доказательство.a b
Метод половинного деления. x
2
a b1
[a; b1 ] a1
[a1 ; b1 ] b2 a1 b1
2
2
n a an bn an bn b
у
lim f (a n ) 0
n
lim f (an ) f (c)
а
у=f(x)
[a1 ; b2 ]
lim(bn an ) 0 lim an lim bn c
n
an c
0
f ( x) 0
а1 а2 b2
c
х
b1
n
n
lim f (bn ) 0
n
lim f (bn ) f (c)
bn c
b
f (c ) 0
х
31.
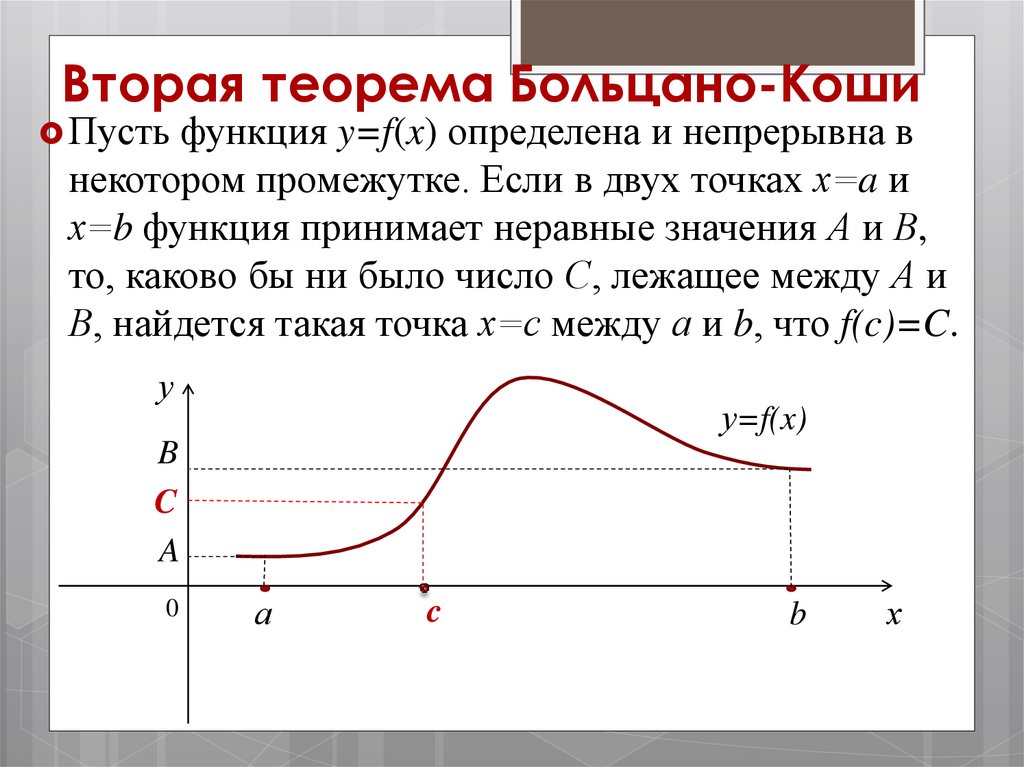
Вторая теорема Больцано-КошиПусть функция y=f(x) определена и непрерывна в
некотором промежутке. Если в двух точках х=a и
х=b функция принимает неравные значения А и В,
то, каково бы ни было число С, лежащее между А и
В, найдется такая точка х=с между а и b, что f(c)=C.
у
у=f(x)
B
C
A
0
а
c
b
х
32.
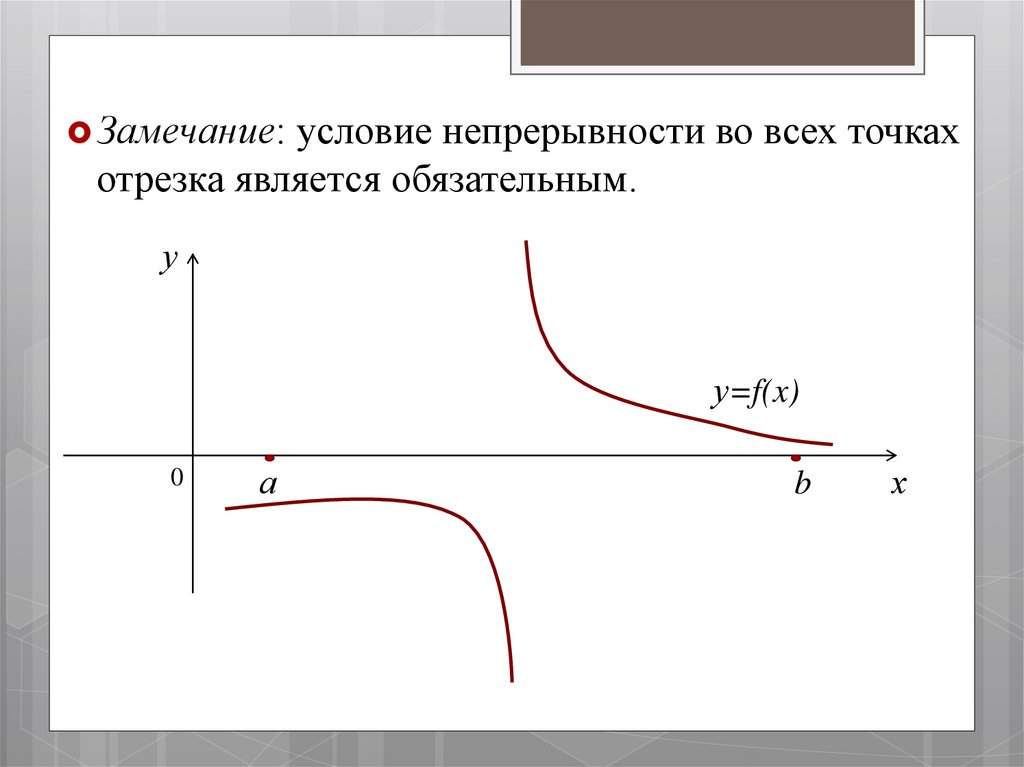
Замечание: условие непрерывности во всех точкахотрезка является обязательным.
у
у=f(x)
0
а
b
х
33.
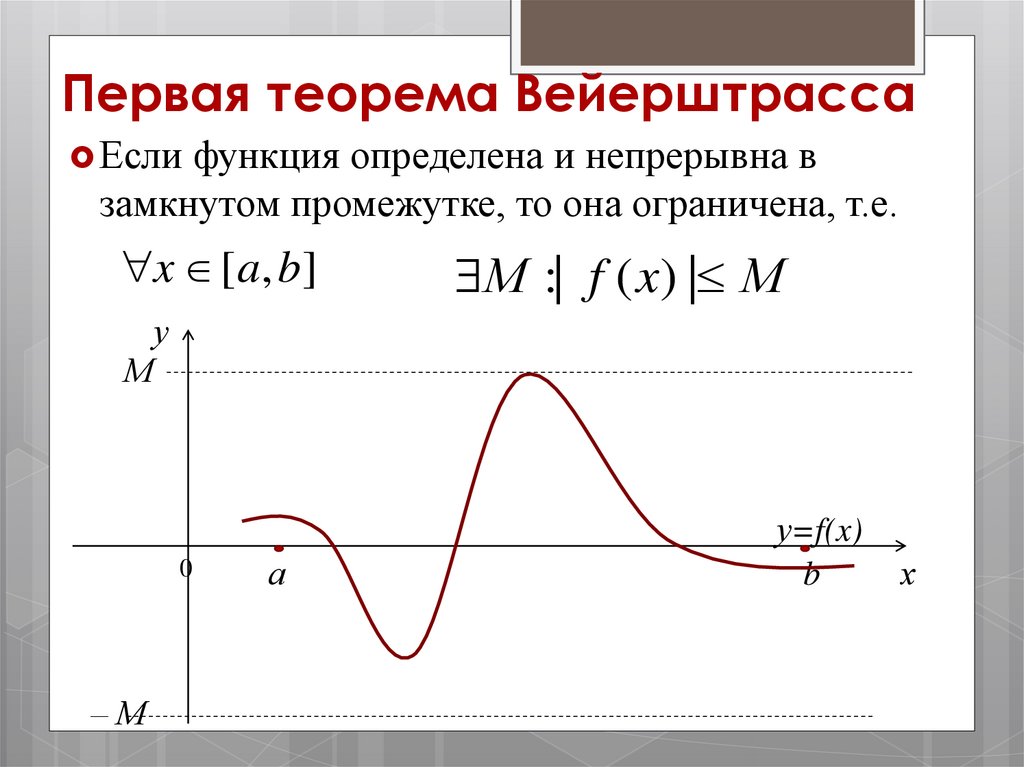
Первая теорема ВейерштрассаЕсли функция определена и непрерывна в
замкнутом промежутке, то она ограничена, т.е.
x [ a, b]
М :| f ( x) | М
у
М
0
–М
а
у=f(x)
b
х
34.
Вторая теорема ВейерштрассаЕсли функция определена и непрерывна в замкнутом
промежутке, то она достигает в этом промежутке своих
точных верхней и нижней граней (наибольшего и
наименьшего значений), т.е.
x1 [a, b] : f ( x1 ) inf f ( x)
у
[ a;b ]
x2 [a, b] : f ( x2 ) sup f ( x)
[ a ;b ]
sup f ( x)
у=f(x)
[ a ;b ]
х1
0
inf f ( x)
[ a ;b ]
а
х2
b
х















 Математика
Математика








